Радиосигналдардың мультифракталдық талдауы

РЕФЕРАТ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
НЕГІЗГІ БӨЛІМ
1 ТАРАУ Радиотехникалық сигналдар. Олардың классификациясы...
2 ТАРАУ Мультифракталдық талдау
2.1 Негізгі түсініктер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
2.2 Ғылыми зерттеу нәтижелері
ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... ..
2
3

4

8
14
19
20

Кейінгі кезде, шуылтәрізді радиосигналдардың негізгі ерекшеліктерін зерттеу мақсаты көптеген ғалымдардың қызығушылығын тудырды. Қазіргі уақытта көбінесе спектрлік және корреляциялық талдауларды зерттеуде пайдаланды, бірақ олар дәлірек сандық нәтижелер бермейді, сондықтан күрделі әдістерді қолдану қажет. Осы жұмыста шуыл қосылған радиоимпульстерді жаңа мультифракталдық талдауды пайдалана отырып зерттеу жүргізілді.
Жұмыста бөлу деңгейіне байланысты шуылтәрізді радиосигналдарды әр топтар бойынша қарастырылды. Радиосигналдардың әрқайсысы үшін мультифракталдық спектрлері, фазалық портреттері мен энтропияның, фракталдық өлшемділіктерінің аффиндік коэффициентіне тәуелдік графикте-рі тұрғызылды. Біртексіздік параметріне түзетулер еңгізу арқылы энтропияны анықтау мүмкіншілігі қарастырылды.

1. Баскаков С.И. Радиотехнические цепи и сигналы /Учеб.для вузов по спец. «Радиотехника». М.:Выс.шк., 2005. 462 с.
2. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы /Ижевск: НИЦ “Регулярная и хаотическая динамика”, 2001, 128 с.
3. Федер Ф. Фракталы. – М.: Мир, 1991. – 254 с.
4. Жанабаев З.Ж., Иманбаева А.К., Алмасбеков Н.Е. Компьютерное моделирование в радиофизике и электронике / Уч. Пособие. Алматы: Қазақ университеті, 2005. 144 с.
5. Жанабаев З.Ж., Наурзбаева А.Ж., Алимгазинова Н.Ш. Информационно-энтропийные характеристики всплесков микроволнового радиоизлучения Солнца/Вестник КазНУ, серия физическая, №2(20), 2005.
6. Жанабаев З.Ж. Квазиканоническое распределение Гиббса и масштабная инвариантность хаотических систем// 5-я Межд. науч. конф. "Хаос и структуры в нелинейных системах. Теория и эксперимент", Астана, 2006, т.1. – С. 15-23.
7. Алимгазинова Н.Ш. Энтропия сигналов солнечного радиоизлучения / Сб. тезисов - Междунар.конгр. студ., магистр. и мол. уч. «Мир науки», Алматы, 2007,С.99.

Пән: Автоматтандыру, Техника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

БІТІРУ ЖҰМЫСЫ

РАДИОСИГНАЛДАРДЫҢ МУЛЬТИФРАКТАЛДЫҚ ТАЛДАУЫ

МАЗМҰНЫ

реферат ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 2
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 3
НЕГІЗГІ БӨЛІМ
1 ТАРАУ Радиотехникалық сигналдар. Олардың классификациясы... 4
2 ТАРАУ Мультифракталдық талдау
2.1 Негізгі түсініктер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 8
2.2 Ғылыми зерттеу нәтижелері 14
ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 19
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... .. 20

Реферат

Беттер саны
20

Суреттер саны
9

Пайдаланған әдебиеттер саны 7

Кiлттi сөздер: ФРАКТАЛ, ФРАКТАЛДЫҚ ӨЛШЕМДІЛІК, МУЛЬТИФРАКТАЛ,
МУЛЬТИФРАКТАЛДЫК ӨЛШЕМДІЛІК

Жұмыстың мақсаты: бейсызық физиканың мультифракталдық талдау әдісін
қолданып, әр түрлі радиосигналдарды зерттеу. Жұмыста радиосигналдардың
аффиндік коэффициенті, энтропиясы, мультифракталдық өлшемділігі,
мультифракталдық спектр функциясы және біртексіздік параметрі анықталды.
Радиосигналдардың фазалық портреттері, мультифракталдық спектрлері,
энтропияның, мультифракталдық өлшемділіктің және біртексіздік параметрінің
аффиндік коэффициентіне тәуелділігі тұрғызылды.

РАДИОСИГНАЛДАРДЫҢ МУЛЬТИФРАКТАЛДЫҚ ТАЛДАУЫ

КІРІСПЕ

Кейінгі кезде, шуылтәрізді радиосигналдардың негізгі ерекшеліктерін
зерттеу мақсаты көптеген ғалымдардың қызығушылығын тудырды. Қазіргі уақытта
көбінесе спектрлік және корреляциялық талдауларды зерттеуде пайдаланды,
бірақ олар дәлірек сандық нәтижелер бермейді, сондықтан күрделі әдістерді
қолдану қажет. Осы жұмыста шуыл қосылған радиоимпульстерді жаңа
мультифракталдық талдауды пайдалана отырып зерттеу жүргізілді.
Жұмыста бөлу деңгейіне байланысты шуылтәрізді радиосигналдарды әр топтар
бойынша қарастырылды. Радиосигналдардың әрқайсысы үшін мультифракталдық
спектрлері, фазалық портреттері мен энтропияның, фракталдық
өлшемділіктерінің аффиндік коэффициентіне тәуелдік графикте-рі тұрғызылды.
Біртексіздік параметріне түзетулер еңгізу арқылы энтропияны анықтау
мүмкіншілігі қарастырылды.

НЕГІЗГІ БӨЛІМ

1 ТАРАУ. РАДИОТЕХНИКАЛЫҚ СИГНАЛДАР. ОЛАРДЫҢ

КЛАССИФИКАЦИЯСЫ

“Сигнал” термині тек ғылыми-техникалық сұрақтарда ғана емес, күнделікті
өмірде жиі кездеседі. Сигналды-хабар, информация деп қабылдауға да болады.
“Сигнал” сөзі латынның “signum”-“белгі беру” сөзінен шыққан.
Сигнал деп мәліметті көрсететін, қабылдайтын немесе беретін кез-келген
бір объектінің уақыт бойынша физикалық күйінің өзгеруін айтады. Хабар,
информация көптеген инженер, математиктер мен философтардың басты
тақырыбына айналды. 40-шы жылдары К.Шеннон информация теориясының бастапқы
тарауын бітіреді.
Сигналдарды кез-келген физикалық процестер сияқты электрондық
оссциллограф, вольтметрлер, қабылдағыштар сынды приборлар және
құрылғылармен зерттеуге болады. Сигналдарды теориялық жағынан ұғыну мен
есептеудің объектісі ретінде қарастыру үшін, сол сигналдың математикалық
моделін көрсету керек.
Сигналдың математикалық моделі, мысалы, аргументі уақыт болып табылатын
функционалдық тәуелділік болып табылады.
Радиотехникада математикалық модель ток, кернеу, электромагниттік өріс
кернеулігі және т.б.-ны суреттейді.
Сигналдарды суреттейтін функциялар заттық, сонымен қатар, комплекстік
мәндерге ие болады.
Сигналдардың математикалық моделін біле отырып, оларды бір-бірімен
салыстырып, айырмашылығын көруге болады.
Радиотехникаға қатысты сигнал болып кез-келген бір тізбектің
қысқыштарының арасындағы кернеу немесе өткізгіштегі ток болып табылады. Бір
уақыт функциясымен сипатталатын мұндай сигналды бірөлшемді деп атайды.
Бірақ, кейде көпөлшемді немесе векторлы сигналдарды қарастыру ыңғайлы.

V(t) = {1(t), 2(t), ..., N(t)}, (1.1)

Мұндағы, N-бүтін санды осындай сигналдың өлшемділігі деп аталады.

Көпөлшемді сигнал ол – бірөлшемді сигналдардың қосындысы болып
табылады. Сондықтан, жалпы жағдайда реті бойынша әрқалай сигналдар
компоненттері бір-біріне тең емес:

{1, 2} {2, 1}.

Сигналдардың көпмүшелік моделінің пайдасы тек ЭВМ көмегімен талданатын
күрделі жүйелердің функциялануы кезінде байқалады.
Радиотехникалық сигналдардың классификациясының келесі принципі сол
сигналдардың кез-келген уақыт мезетінде мәндерінің болу-болмауын тура
болжауында жатыр.
Егер сигналдың математикалық моделі осы болжамды жүзеге асыра алса,
онда сигнал детерминді деп аталады. Оның әдістері әр-түрлі болуы мүмкін:
математикалық формула, есептегіш алгоритм және ауызша суреттеу.
Қатаң айтқанда, детерминді сигналдарға тең жауап беретін детерминді
процестер жоқ. Жүйенің өзін қоршаған физикалық объектілермен әсерлесуі,
хаостық жылулық флуктуациялардың болуы және де жүйенің бастапқы күйі
жайындағы мағлұматтың толық болмауы – мұның бәрі реалдық сигналдарды
уақыттың кездейсоқ функциясы ретінде қарастыруға болады.
Радиотехникада “кездейсоқ сигналдар” көбінесе өздерін шуыл ретінде
білдіреді. Сол шуыл қабылданған тербелістен информацияны бөліп алу кезінде
қиындық туғызады. Шуылмен күрес мәселесі – радиотехниканың ең күрделі
мәселелерінің бірі болып табылады.
Бір жағынан “кездейсоқ сигнал” түсінігі қатаң секілді болып көрінуі
мүмкін, шындығында олай емес. Мысалы, ғарыштық сәуле көзіне бағытталған
радиотелескоп қабылдағышының шығысындағы сигнал өзімен бірге сол объект
жайлы әр-түрлі информацияға ие хаостық тербелісті білдіреді.
Детерминді және кездейсоқ сигналдар арасында өте алмайтын шекара жоқ.
Егер, бізге керекті белгілі бір формалы сигналдың деңгейінен шуыл деңгейі
аз болса, қарапайым детерминді модель көмегімен алға қойылған есептерді
шешуге болады.
Соңғы он жыл бойы дамыған кездейсоқ сигналдардың қасиеттерін талдау
үшін қолданылатын статикалық радиотехника әдістерінің көптеген сынды
қырлары бар және ықтималдықтар теориясы мен кездейсоқ процесстер
теориясының математикалық аппаратында бастамасын алады.
Радиотехниканың ең негізгі сигналдар класы – импульстер болып
табылады,яғни, уақыттың соңғы бөлігінің аралығындағы тербелістер. Сонымен
қатар видеоимпульстер және радиоимпульстер болады. Бұл басты импульстер
түрлері арасындағы айырмашылығы келесіде. Егер, иВ (t) – видеоимпульс
болса, онда соған қатысты радиоимпульс келесідей болады:
и p (t) = иВ (t) cos (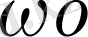t + 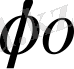) (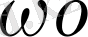- жиілік және -
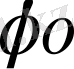бастапқы фаза кездейсоқ). Сонымен қатар, иВ (t) функциясы радиоимпульстің
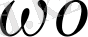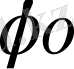қисық сызығы дейміз, ал cos (t + ) функциясын оның толықтырылуы
дейді.
Техникалық есептеулерді импульстің структурасы жайлы дерек беретін
толық математикалық модель орнына көбінесе сандық параметрлермен қолданады.
Ол сигналдың формасы жайлы қарапайым түсініктеме береді. Формасы трапецияға
өте ұқсас видеоимпульстер үшін оның амплитудасын(биіктігін) А анықтау
қажет. Уақыттық параметрлер ішінен импульс ұзақтылығын , фронт
ұзақтылығын , кесінді ұзақтылығын бөліп айтуға болады.
Радиотехникада амплитудалары микровольт бөліктерінің бірнеше киловольтта
жататын, ұзақтылығы наносекунд бөлігі болатын кернеу импульстерімен
байланысты.

Аналогты, дискретті, сандық сигналдар

Радиотехникалық сигналдардың классификацияға бөліну принциптерін
түйіндей келгенде, келесі тұжырымды атап айтуға болады. Сигналды
түрлендіретін физикалық процесс сол сигналдың мәндерін кез-келген уақыт
моментінде өлшеуге болатындай уақыт бойынша дамиды. Сигналдардың мұндай
класын аналогты (континуалды) деп атайды. “Аналогты сигнал” термині, сол
сигналдың өтіп жатқан физикалық құбылысқа аналогты түрде ұқсастығын
көрсетеді.
Бастапқыда, радиотехникада тек аналогты типті сигналдарды қарастырды.
Мұнда сигналдар қиын емес техникалық есептерді (радиобайланыс, теледидар
және т.б) өте жақсы шешеді. Аналогты сигналдарды генерациялауға, сигналды
қабылдап және оны өңдеуге болады. Аналогты жүйе орнына дискреттік
сигналдарды қолданатын импульстік жүйелер келеді. Дискретті Sд (t)
сигналдың математикалық моделі – ол уақыт бойынша {ti} (i – бүтін сан)
нүктелердің санақ жиыны. Олардың әр қайсысында S i сигналдың санақ мәні
анықталған. Әр сигнал үшін дискреттелу қадамы = ti+1 – ti тұрақты.
Уақыт бойынша жылдам өзгеретін аналогты сигналдардың дискреттелуі аз
ғана қадам талап етеді.
Дискретті сигналдардың ерекше бір түрі – сандық сигналдар. Олардың
соңғы мәндерінің формасы сан түрінде берілген. Соңғы уақытта сандық
сигналдар жүйелері көпшілікке мәлім бола бастады. Ол микроэлектроника мен
интегралдық схемотехникадағы ғылыми жетістіктермен байланысты. Шындығында,
кез-келген дискретті немесе сандық сигнал аналогты сигнал болып табылады.
Уақыт бойынша баяу өзгеретін S (t) аналогты сигналға оның дискретті
көрінісін көрсетуге болады [1].

2 ТАРАУ. МУЛЬТИФРАКТАЛДЫҚ ТАЛДАУ

2.1. Негізгі түсініктер

Фрактал деп өз-өзіне ұқсас қасиеті бар қисық формаға ие сызықтар,
беттерді айтады. Фрактал сөзі латынның “fractus” сөзінен шыққан. Фракталдың
өз-өзіне ұқсастық қасиеті фракталдың ең негізгі қыры болып табылады. Егер,
үлкейтіп көретін болсақ, фракталдың кішкене фрагменттерінің үлкеніне
ұқсайтынын көреміз [2,3].
Айталық, тура өз-өзіне ұқсастық қасиеті тек регулярлы фракталдарға ғана
тиесілді. Егер детерминді құрылу әдісінің алгоритміне бір кездейсоқтық
элементін қосатын болсақ, онда біз кездейсоқ фрактал аламыз. Олардың
регулярлы фракталдардан негізгі айырмашылығы мынада. Өз-өзіне ұқсастық
қасиеті тек объектінің статикалық тәуелсіз байқалуларының орташалануынан
кейін болады.
Мультифракталды сипаттау үшін бір ғана емес, көп фракталдық
өлшемділіктер жиыны керек. Табиғи фракталдар-дың көбі, негізінде,
мультифракталдар. Қысқаша айтқанда, мультифрактал ол–біртекті емес фрактал
болып табылады.
Жоғарыда айтқандай, регулярлық фракталдарға қарағанда бір ғана
фракталдық өлшемділік D ғана емес, шексіз осындай фракталдық өлшемділіктер
жиынымен ғана түсіндіруге болады. Осындай фракталдар статикалық қасиеттерге
де ие болады.

Фракталдық өлшемділік

Ол L өлшемді Евклид кеңістігінде өлшемділігі d (d = 1–сызық, d = 2 -
жазықтық,d=3–үшөлшемді кеңістік) белгілі бір шектік аумағын қамтитын
фракталдық объектіні қарастырайық. Оның құрылу барысының белгілі бір
кезеңінде ол N1 нүктелерден құралған жиынды берсін. Біз соңында
N болады деп болжам жасаймыз. l ауданының көлемі ( d және
( жағы бар кубтық ұяшықтарға бөлеміз. ( азайған сайын ауданды қамтитын
N((), ұяшықтар саны дәрежелік заң бойынша өзгереді.

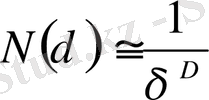(2.1)
D дегеніміз хаусдорф немесе фракталдық өлшемділік деп аталады. (2.1)–ді
логарифмдеп және ( нөлге ұмтылса, оны былай жазамыз

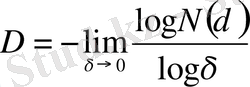(2.2)

D–шамасы қарастырып отырған объектінің локалдық сипаттамасы болып табылады
[3].
Евклид кеңістігіндегі L өлшемді фракталдық объектіні қарастырамыз. Біз
енді тек аз дегенде бір нүкте болатын бос емес ұяшықтарды қараймыз. Бос
емес i ұяшықтар санының нөмірі i = 1, 2,... N(() арасында өзгерсін.
Мұндағы, N(()-( ұяшық нөмірінің өлшеміне тәуелді бос емес ұяшықтардың
саны. Егер ұяшықтар бойынша нүктелер үлестірілуі бірдей болмаса, ондай
фракталды біртексіз фрактал дейміз. Мультифракталды сипаттау үшін Dq
жалпыланған фракталдық өлшемділіктерді еңгіземіз.
Егер ni(() i нөміріне сәйкес ұяшықтағы нүктелер мөлшері болса, онда

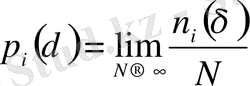(2.3)
pi(() – жиыннан кездейсоқ таңдап алынған нүктенің i ұяшығында болу
ықтималдылығы. Кеңейтілген фракталдық өлшемділіктер спектрі Dq келесі
қатынаспен анықталады

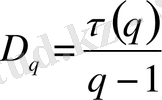(2.4)
мұндағы q – q + интервалында кез-келген мән қабылдайды, сонда
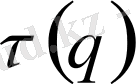мына түрде жазылады

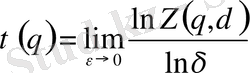(2.5)
мұндағы 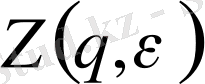- кеңейтілген статикалық сумма:

.
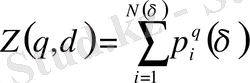(2.6)
Егер Dq = D = const болса, яғни q дан тәуелді болмаса, онда мұндай нүктелер
жиынын бір ғана D фракталдық өлшемділігі бар қарапайым, регулярлы фрактал
деп атаймыз. Керісінше, егер Dq функциясы q бойынша өзгеретін болса, оны
мультифрактал дейміз. 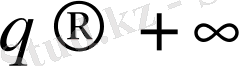кезде кеңейтілген статикалық суммаға (2.6) тек
ең көп бөлшектері бар ұяшықтар саны басты үлес қосады. Оның толтырылу
ықтималдылығы pi болып табылады. Осыған орай Dq функциясы l
жиынындағы нүктелер санының біртексіздігін көрсетеді.
Жалпы жағдайда, мультифрактал бейсызық 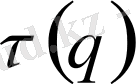(2.5) функциямен
анықталады. Ол ( ( 0 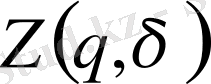статикалық сумманы сипаттайды. Бірақ нүктелердің
үлестірілуін тек 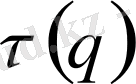ғана емес, оның туындысы керек

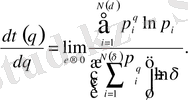(2.7)
бұл туынды q мен бірге өзгереді.
q = 1 кезінде фракталдық өлшемділік мынаған тең
.
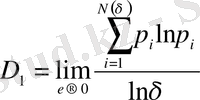(2.8)

Бұл формуланың алымы фракталдық жиын энтропиясы болып табылады.
Соңында, кеңейтілген фракталдық өлшемділік D1 энтропиямен S(() мына
қатынаспен сипатталады

.
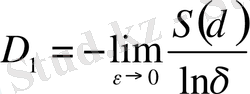(2.9)

Мультифракталдық спектр функциясы

Жалпы түсінік бойынша Dq шамалары, қатаң айтқанда, фракталдық
өлшемділіктер емес. Сондықтан солармен бірге мультифракталдық жиынды
сипаттау үшін мультифракталдық спектр функциясын f(() қолданамыз. Оны
мультифрактал сингулярлығының спектрі деп те атайды. Біз осы f(() шамасын
белгілі бір жалпы жиынның біртекті фракталдық L жиыншасының хаусдорфтық
өлшемділігіне тең екенін көреміз. Ол q шамасын беру арқылы бүкіл статикалық
суммаға үлкен үлесін қосады.
Өз-өзіне ұқсас жиындар үшін рi ( - ұяшық өлшеміне тәуелділігі
дәрежелік мәнге ие болады:

(2.10)

мұндағы (i – дәреже көрсеткіші (i- әр түрлі ұяшық үшін әрқалай). Біртекті
фрактал үшін (i дәреже көрсеткіштері бірдей және D фракталдық
өлшемділігіне тең.

(2.11)
Бұл жағдайда ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.