Ықтималдықтар теориясы.Негізгі түсініктері.Кездейсоқ шаманың сандық сипаттамасы.Математикалық күтім

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым министірлігі.

Семей мемлекеттік Шәкәрім атындағы университеті.

СӨЖ

Тақырыбы : Ықтималдықтар теориясы. Негізгі түсініктері. Кездейсоқ шаманың сандық сипаттамасы. Математикалық күтім.

Орындаған:Хуантай А. Ж

Тексерген:Мұхаметов Е. М

Семей- 2015ж

Жоспар:

1. Кіріспе.

2. Негізгі бөлім.

3. Қорытынды бөлім.

Пайдаланылған әдебиеттер тізімі:

Ықтималдылық Теориясы - кездейсоқ бір оқиғаның ықтималдығы бойынша онымен қандай да бір байланыста болатын басқа бір кездейсоқ оқиғаның ықтималдығын анықтауға мүмкіндік беретін математика білімі. Ықтималдылық теориясында кездейсоқ құбылыстардың заңдылығы зерттеледі. Кездейсоқ құбылыстарға анықталмағандық, күрделілік, көп себептілік қасиеттері тән. Сондықтан мұндай құбылыстарды зерттеу үшін арнайы әдістер құрылады. Ол әдістер мен тәсілдер Ықтималдылық теориясында жасалынады. Мысалы, біркелкі болып келетін кездейсоқ құбылыстарды жан-жақты бақылай отырып қандай да болмасын бір заңдылықты (тұрақтылықты), яғни статистик. заңдылықты байқаймыз. Ықтималдылық теориясының негізгі ұғымдары элементар ықтималдылық теориясы шегінде қарапайым түрде анықталады. Элементар ықтималдылық теориясында қарастырылатын әрбір сынау (Т) Е1, Е2, . . . , Еs оқиғаларының тек қана біреуімен ғана аяқталады. Бұл оқиғалар сынау нәтижесі (қорытындысы) деп аталады. Әрбір Еk нәтижесімен оның ықтималдығы деп аталатын рk оң саны байланыстырылады. Бұл жағдайда рk сандарының қосындысы бірге тең болуы керек. А оқиғасы тең мүмкіндікті бірнеше оқиғаларға (Еі, Еj, …, Еk) бөлінеді және олардың кез келген біреуінің (не Еі, не Еj, …, не Еk) пайда болуынан А оқиғасының пайда болуы шығады. Сынау нәтижесінде А оқиғасы бөлінетін мүмкін мәндері (Еі E, j, …, Еk) осы оқиғаға (А-ға) қолайлы жағдайлар деп атайды. Анықтама бойынша А оқиғасының р(А) ықтималдығы оған қолайлы жағдайлар нәтижелері ықтималдықтарының қосындысына тең деп ұйғарылады: P(A) =Pі+Pj+ . . . +Pk (1) Дербес жағдайда р1=р2= . . . =рs=1/s болғанда Р(А) =r/s (2) болады. А оқиғасына қолайлы жағдайлар нәтижесі санының (r) барлық тең мүмкіндікті нәтижелер санына (s) қатынасы А оқиғасының ықтималдығы деп аталады. (2) формула ықтималдықтың классикалық анықтамасын өрнектейді. Бұл анықтама “ықтималдық” ұғымын дәл анықтамасы берілмейтін “тең мүмкіндік” (тең ықтималдық) ұғымына келтіреді. Тең мүмкіндік немесе тең ықтималдық ұғымдары алғашқы ұғымдарға жатады. Олар логикалық (формалды) анықтама беруді қажет етпейді. Егер жалпы сынау нәтижесінде бірнеше оқиғалар пайда болса және олардың біреуінің пайда болу мүмкіндігінің екіншісіне қарағанда артықшылығы бар деп айта алмасақ (яғни сынаулар нәтижесінде симметриялы қасиеті болса) онда мұндай оқиғалар тең мүмкіндікті делінеді. Элементар ықтималдылық теориясының негізгі формулаларының қатарына ықтималдылықтардың толық формуласы да жатады: егер А1, А2, . . . , Аr оқиғалары қос-қостан үйлесімсіз болып әрі олардың бірігуі нақты бір оқиға болса, онда кез келген В оқиғасының ықтималдылығы: Р(В) = 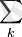$\sum_{k}$ Р(В/Аk) Р(Аk) қосындысына тең болады. Ықтималдылық теориясының негізін құрудағы қазіргі ең жиі тараған логик. сұлбаны 1933 ж. кеңес математигі А. Н. Колмогоров жасаған. Бұл сұлбаның негізгі белгілері төмендегідей. Ықтималдылық теориясының тәсілдерімен қандай да болмасын нақты бір есепті зерттегенде ең алдымен U элементтерінің (элементар оқиғалар деп аталатын) U жиыны бөлініп алынады. Кез келген оқиға оған қолайлы жағдайлардың элементар оқиғаларының жиыны арқылы толық сипатталынады. Сондықтан ол элементар оқиғалардың белгілі бір жиыны ретінде де қарастырылады. Белгілі бір А оқиғалары мен олардың ықтималдығы деп аталатын Р(А) сандары байланыстырылады және олар мынадай шарттарды қанағаттандырады:

,
Р(U) =1,
Егер А1, . . . , Аn

оқиғалары қос-қостан үйлесімсіз болып, ал А - олардың қосындысы болса, онда: Р(А) =Р(А1) +Р(А2) + . . . +Р(Аn) болады. Толық матем. теория құру үшін 3-шарттың қос-қостан үйлесімсіз оқиғалардың шектеусіз тізбегі үшін де орындалуы қажет. Теріс еместік пен аддитивтілік қасиеттері - жиын өлшеуінің негізгі қасиеттері. Сондықтан Ы. т. формалды түрде өлшеуіштер теориясының бөлігі ретінде де қарастырылуы мүмкін. Бұл тұрғыдан қарағанда Ы. т-ның негізгі ұғымдары жаңа мәнге ие болады. Кездейсоқ шамалар өлшемді функцияларға, ал олардың матем. үміті А. Лебегтің абстракт интегралына айналады, тағы басқа. Бірақ ықтималдылық теориясы мен өлшеуіштер теориясының негізгі мәселелері әр түрлі болып келеді. Ықтималдылық теориясының негізгі, өзіне тән ұғымына оқиғалардың, сынаулардың, кездейсоқ шамалардың тәуелсіздік ұғымы жатады. Сонымен бірге ықтималдылық теориясында шартты үлестіру, шартты матем. үміт, тағы басқа объектілер де зерттеледі. Ықтималдылық теориясы 17 ғ-дың орта кезінде пайда болды. Ықтималдылық теориясы 17 ғ-дың орта шенінде әйгілі ғалымдар Б. Паскаль (1623 - 62) мен П. Ферма (1601 - 65), Х. Гюйгенс (1629 - 95), Я. Бернулли (1654 - 1705), Муавр (1667 - 1754), Гаус (1777 - 1885) еңбектерінде пайда болып, әрі қарай дамыған. Қазір Лаплас (1812) пен Пуассон (1837) теоремаларының дәлелденуі осы кезеңге жатады; ал А. Лежандр (Франция, 1806) мен К. Гаусс (1808) ең кіші квадраттар тәсілін жетілдірді. Ықтималдылық теориясы тарихының үшінші кезеңі (19 ғ-дың 2-жартысы) негізінен орыс математиктері П. Л. Чебышев, А. М. Ляпунов және А. А. Марков (үлкені) есімдеріне байланысты. 19 ғ-дың 2-жартысында Батыс Еуропада матем. статистика (Белгияда А. Кетле, Англияда Ф. Гальтон) мен статис. физика (Австрияда Л. Больцман) бойынша көптеген еңбектер жазылды. Бұл еңбектер (Чебышев, Ляпунов және Марковтардың негізгі теор. еңбектерімен қатар) ықтималдылық теориясы тарихының төртінші кезеңінде ықтималдылық теориясының шешілуге тиісті мәселелерінің аясын кеңейтті. Бұл кезеңде шет елде де (Францияда Э. Борель, П. Леви, т. б., Германияда Р. Мизес, АҚШ-та Н. Винер, т. б., Швецияда Г. Крамер) КСРО-да өте маңызды зерттеулер жүргізілді. Ықтималдылық теориясының жаңа кезеңі С. Н. Бернштейннің зерттеулерімен байланысты. Ресейде А. Я. Хинчин мен А. Н. Колмогоров ықтималдылық теориясының мәселелеріне нақты айнымалы функциялар теориясының тәсілдерін қолдана бастады. Кейінірек (30-жылдары) олар процестер теориясының негізін қалады. Қазақстан ғалымдары да (І. Б. Бектаев, Б. С. Жаңбырбаев) Ықтималдылық теориясы бойынша зерттеулер жүргізіп келеді.

Кездейсоқ шамалар жайында түсiнiк . Дискреттi кездейсоқ шамалардың үлестiрiм заңдары Анықтама. Мүмкiн болатын мəндерден тəжiрибе нəтижесiне байланысты бiр мəндi қабылдайтын айнымалыны кездейсоқ шама деп атайды. Яғни, кездейсоқ шама сан мəндерiн қабылдайды, бірақ дəл қандай мəн қабылдайтынын алдын ала айта алмаймыз. Кездейсоқ шамаларды жəне басқа да бас əрiптермен, ал олардың қабылдайтын мəндерiн жəне басқа да кiшi əрiптермен белгiлеймiз. Z, Y, X z, y, x Қабылдайтын мəндер жиынына орай кездейсоқ шамаларды екi топқа бөледi: дискреттiк жəне үзiлiссiз. Егер кездейсоқ шамалардың мəнiн тiзбек түрiнде жазуға болса, онда оны дискреттiк деп, ал мəндерi белгiлi бiр аралықта жатса, онда оны үзiлiссiз деп атайды. Кездейсоқ шаманың мəндерi мен олардың ықтималдықтарының арасындағы сəйкестiктi дискреттi кездейсоқ шаманың үлестiрiм заңы немесе функциясы деп атайды. Бұл сəйкестiк таблица, график жəне аналитикалық түрiнде берiлуi мүмкiн. Таблица түрiнде функция х1 х2 х3 … хn p1 p2 p3 … pn немесе үлестiрiм заңы осылай берiледi. Бұл жерде, бiрiншi жолда кездейсоқ шама x-тың мəндерi, екiншi жолда сол мəндердiң қандай ықтималдықтармен қабылданатыны жазылған. Кездейсоқ шама Х-тың мəндерi толық жүйе жасайтын болғандықтан, ) n, . . . 2, 1i, 0P(1P . . . PP . 21 n i =≥=+++ Үлестiрiм заңның мысалы ретiнде биномиальдық заңдылықты келтiрейiк. Бұл заңда, ықтималдықтарды Бернулли формуласымен есептейдi жəне мына түрде: Х n −1n − 2n … k … 0 Р n P qnp −1n 22n2nn qpC −− … knkkn qpC − … n q кестесi жазылады.

Дискреттi кездейсоқ шаманың сандық сипаттамалары жəне олардың қасиеттерi Кездейсоқ шаманы үлестiрiм заңы толық сипаттайтынын жоғарыдан бiлемiз. Бірақ кейде заңдылық толық берiлмегенде, басқа шамалар арқылы кездейсоқ шаманы зерттеуге болады.

Күнделікті өмірде орындалатын да, орындалмайтын да оқиғалар жиі кездеседі. Таңертең тұрып терезеден далаға қарасақ, далада күн ашық болуы да, бұлтты болуы да, жаңбыр жаууы да, қар жаууы да мүмкін. Бұлардың бәрінің орындалу мүмкіндіктері тең. Мұнда бірі орындалса, басқалары орындалмайтын жағдай бар. Және олар кездейсоқ оқиға болып табылады. Асықты лақтырғанда оның бүк, шік, тәйкі немесе алшы жағы жоғары қарап түсуі де - кездейсоқ оқиға. Сонымен, кездейсоқ оқиға деп белгілі бір тұрақты жағдайда орындалуы мүмкін немесе орындалмауы мүмкін оқиғаны айтады.

Мысал 1:

Асықты лақтырып ойнағанда, ол асықтың бүк жағы жоғары қарап немесе шік жағы жоғары қарап, әлде болмаса, тәйкі жағы немесе алшы жағы жоғары қарап түсуі мүмкін. Мұнда бірі орындалса, басқалары орындалмайтын жағдай бар. Асықты лақтырғанда оның бүк, шік, тәйкі немесе алшы жағы жоғары қарап түсуі кездейсоқ оқиға болып табылады.

Біз қадағалап отырған нәтиже қанша рет шығатындығын анықтау үшін бірнеше рет бір-біріне тәуелсіз тәжірибелер жүргізіледі. Тәжірибе деп нәтижесін байқауға болатын объектіні түсінеміз. Мысалы: емтихан тапсыру, мылтықтан оқ ату, ойын тасын лақтыру, т. б.

Негізі тәжірибеге дейін бізге қолайлы оқиғаның орындалатынын, не болмаса орындалмайтынын анықтау мүмкін емес, оны тек тәжірибе соңында ғана көреміз. Біз ықтималдықтар теориясында кездейсоқ тәжірибеге қатысты барлық оқиғаларды кездейсоқ оқиғалар дейміз және кездейсоқ оқиға болып мына оқиғалар саналады:

1. жалған - ешқашан орындалуы мүмкін емес оқиға,

2. айқын - әрбір тәжірибе барысында орындалатын оқиға.

Мысал 2 :

Жұмыртқаны пісіргенде пайда болатын оқиғаларды қарастырайық:

А=жұмыртқаның пісуі ;

В=жұмыртқаның піспеуі ;

С=піскен жұмырқадан балапанның шығуы

А, В оқиғалары - кездейсоқ оқиғалар, яғни айқын оқиғалар, С оқиғасы - жалған оқиға.

Мысал 3 :

Немесе ойын тасын (біртекті куб) тастағанда, ол алты жағына түсуі мүмкін. Егер оларды 1, 2, 3, 4, 5, 6 деп белгілесек, 7 түсуі жалған, осы алты жағының бірі түсуі айқын оқиғалар.

Ал жұп ұпайдың түсуі, түспеуі кездейсоқ оқиға, өйткені оның яғни 2, 4, 6 жағының түсуін алдын-ала болжай алмаймыз. Ол нәтижеге байланысты. Нәтиже дегеніміз, кездейсоқ тәжірибені аяқтайтын және бір-бірін өзара жоққа шығаратын нұсқалардың бірі.

Мысалы 4:

1. Тиынды лақтырғанда - екі нәтиже: елтаңба және цифр жағының түсуі

2. Ойын тасын лақтырғанда - 6 нәтиже: 1, 2, 3, 4, 5, 6 жағының түсуі

Кездейсоқ оқиға және ықтималдық