Адамс айырымдық әдісімен жеке туындылардағы дифференциалдық теңдеулерді шешу және интерполяция негіздері


Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
СЕМЕЙ ҚАЛАСЫНЫҢ ШӘКӘРІМ АТЫНДАҒЫ
МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ
Инженерлік-технологиялық факультет
(факультет атауы)
Техникалық физика және жылуэнергетика
(кафедраның аталуы)
5В071700 - «Жылуэнергетика»
(шифр, мамандықтың аталуы)
СӨЖ
Жылуэнергетикадағы машиналық графиканың элементтері мен АЖЖ негіздері
(пән аты)
Жеке туындылардағы дифференциал теңдеулерді шешу
(тақырыбы)
Орындаған:
ТЭ-417 тобының студенті:
Шарипова А. А.
Тексерген:
аға оқытушы: Нургалиев Д. Н.
Семей 2015 ж.
МАЗМҰНЫ
КІРІСПЕ3
1 ЖЕКЕ ТУЫНДЫЛАРДАҒЫ ДИФФЕРЕНЦИАЛДЫ ТЕҢДЕУЛЕРДІ АЙЫРЫЛЫМ ТӘСІЛДЕРІМЕН ШЕШУ4
2 ФУНКЦИЯНЫҢ ИНТЕРПОЛЯЦИЯСЫ8
2. 1 Лагранж түріндегі интерполяциялық полином9
ҚОРЫТЫНДЫ11
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР12
Дифференциалдық теңдеулер - ізделінетін функцияны оның әр түрлі ретті туындыларымен (немесе дифференциалдарымен) және тәуелсіз айнымалылармен байланыстыратын теңдеулер. Дифференциалдық теңдеулер 17 ғасырдың соңында механика, т. б. жаратылыстану пәндерінің талабына сәйкес интегралдық есептеу және дифференциалдық есептеумен қатар пайда болды. Қарапайым дифференциалдық теңдеулер Ньютонның және неміс математигі Лейбництің) еңбектерінде кездеседі. “Дифференциалдық теңдеулер” терминін ғылымға Лейбниц енгізген (1676) . Тәуелсіз бір айнымалыға тәуелді бір немесе бірнеше функциялардың туындылары бар дифференциалдық теңдеулерді жай дифференциалдық теңдеу деп, ал тәуелсіз бірнеше айнымалыға тәуелді функциялардың дербес туындылары бар дифференциалдық теңдеулерді дербес туындылы дифференциалдық теңдеу деп атайды. Дифференциалдық теңдеулерге енетін туындылардың реті дифференциалдық теңдеулердің реті делінеді.
1 ЖЕКЕ ТУЫНДЫЛАРДАҒЫ ДИФФЕРЕНЦИАЛДЫ ТЕҢДЕУЛЕРДІ АЙЫРЫЛЫМ ТӘСІЛДЕРІМЕН ШЕШУЖеке туындылардағы дифференциалды теңдеулерді айырылым тәсілдерімен шешуде Адамс әдісін қарастырайық.
Рунге-Кутта әдісінің негізгі кемшілігі болып, дифференциалдық теңдеудің бір жаңа шешімін алу үшін теңдіктің оң жағын бірнеше нүктелерде есептеуге тура келетіні.
Айырымды әдістері сонымен қатар, сандық әдістер болып табылады, яғни интеграл аралығында х 0 , х 1 , . . . , х n , . . . түйіндегі мәнді табуға мүмкіндік береді. Айталық, мына түрдегі дифференциалдық теңдеуді шешейік:
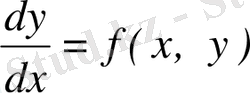
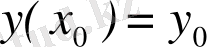
((1)
(2)
Айырымды әдістерді, ізделініп отырған функцияның мәндері және бастапқы шарттарымен берілген Коши есебіне қолдануда кейбір қосымша нүктелердегі у ( х ) ізделініп отырған мәндерін білу қажетті. Бұл шешімдердің алдында қарастырылған әдістермен анықтауға болады.
Айталық, x 1 = x 0 + h , x 2 = x 0 + 2h , . . . , x n = x 0 + nh нүктелеріндегі y 1 , y 2 , . . . , y n жуықтау шешімінің п мәндері белгілі. Нүктесі шешімін табуға тура келетін келесідегідей болып табылады. [ x n , x n+1 ] аралығында (1) өрнегін интегралдап, соған тең интегралдық теңдеуін аламыз:
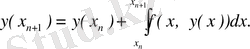
(3) өрнегімен у ( х i ) шешімінің келесі есептеулері үшін қолдануға болады. Ол үшін (3) өрнегіндегі интегралды есептеу қажет. Оны дәл есептеу мүмкін емес, өйткені интеграл асты функциясына у ( х ) белгісіз функция кіреді. Интеграл астындағы функцияны интерполяциялық полиноммен алмас-тырып, интегралды жуықтап есептейміз. Мұнда алдыңғы f ( x , у ( х ) ) мәндерімен көрсетуге болады. Егер жақын мәндерімен, яғни f ( х n , у ( х n ) ), f ( х n- 1 , у ( х n- 1 ) ) мәндерімен пайдалансақ, ең жақсы нәтиже аламыз. (3) өрнегінде х = x n + ht айнымалыларына алмастыру енгіземіз. Сонда
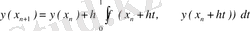
формуласын аламыз. Интеграл астындағы функцияның жуық-тауын есептеу үшін кез келген интерполяциялық формуланы алуға болады. Кесте соңындағы Ньютон формуласын интерполяциялау үшін аламыз
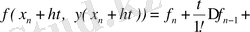
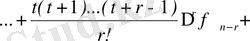
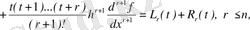
мұндағы
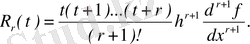
Бұл өрнектерді (4) формуласына қойып,
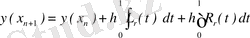
табамыз. Бірінші интегралдың оң жағын интегралдауды орындап,
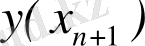

теңдеуін аламыз. Мұндағы
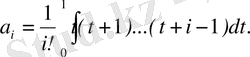
Тәжірибелік есептеулерде (8) формуласына кіретін ақырғы айырымдар ыңғайлы, оларды түйіндегі функцияның мәндері арқылы сипаттап, нәтижесінде
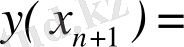
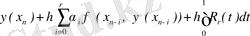
теңдеуін аламыз.
Қалдық мүшедегі интегралды есептеу мүмкін болмайтын-дығын ескере отырып, оны алып тастайды, нәтижесінде Адамс әдісіндегі есептеу схемасын аламыз
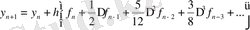
немесе
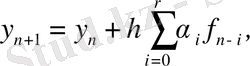
Мұндағы
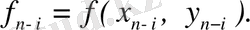
Адамс әдісі үшін қателік бағасын құрайық. Айталық, (1) өрнегінің оң бөлігіндегі f ( х, у ) келесі шарттарды қанағат-тандырады деп шамалайық:
1. f ( х, у ) - D аумағындағы үздіксіз функция;
2.
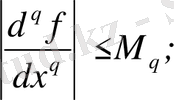
f
(
х, у
) функциясы
C
сияқты тұрақтысымен Липица шартын қанағаттандырады.
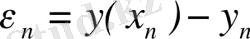 деп белгілеп, (5) өрнегінен (7) теңдігін аламыз
деп белгілеп, (5) өрнегінен (7) теңдігін аламыз
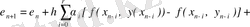
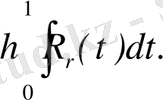
Модуль бойынша Липица шартын ескере
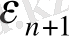 -ны бағалайық. Сонда
-ны бағалайық. Сонда
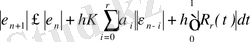
теңдеуін аламыз. Мұндағы
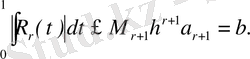 Нәтижесінде келесідегідей қателіктің рекуррентті бағасын аламыз:
Нәтижесінде келесідегідей қателіктің рекуррентті бағасын аламыз:
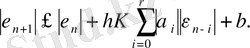
Егер (15) теңдеуде
 белгісінің орнына = белгісін қойсақ, онда алынған теңдік жоғарғы
белгісінің орнына = белгісін қойсақ, онда алынған теңдік жоғарғы
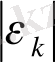 шекарасының теңдеуі екенін көрсетуге болады. Бұл
шекарасының теңдеуі екенін көрсетуге болады. Бұл
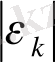 жоғарғы шекараны
жоғарғы шекараны
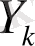 арқылы белгілесек, онда
арқылы белгілесек, онда
 үшін келесі теңдеу дұрыс болып саналады:
үшін келесі теңдеу дұрыс болып саналады:
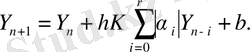
Өйткені
у
0
,
у
1
,
. . .
,
у
n
мәндері Адамс әдісімен есептемес бұрын белгілі, онда
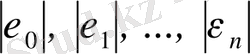 белгісіз деп есептеп және
Y
0
,
Y
1
,
. . .
,
Y
n
, сәйкесінше, онда (8. 29) формуласы арқылы
Y
n
+1
,
Y
n
+2
, . . . табуға болады. (8. 29) теңдігін айырымды теңдеулерді шешу ережелері бойынша шешуге болады және Адамс әдісінің қателік бағасын алуға болады. Айталық,
i
= 0, 1, . . . ,
п
кезінде
белгісіз деп есептеп және
Y
0
,
Y
1
,
. . .
,
Y
n
, сәйкесінше, онда (8. 29) формуласы арқылы
Y
n
+1
,
Y
n
+2
, . . . табуға болады. (8. 29) теңдігін айырымды теңдеулерді шешу ережелері бойынша шешуге болады және Адамс әдісінің қателік бағасын алуға болады. Айталық,
i
= 0, 1, . . . ,
п
кезінде
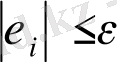 , онда
, онда
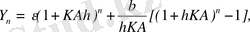
Мұндағы
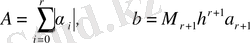
(16) теңдеудің шешімі болып табылады. Осы шешімнің негізінде келесі қателік бағасын аламыз:
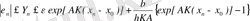
Егер,
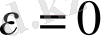 деп қойсақ, онда бастапқы беттегі есептеуде қате аз болады деп есептейміз, яғни алынған қателіктен
деп қойсақ, онда бастапқы беттегі есептеуде қате аз болады деп есептейміз, яғни алынған қателіктен
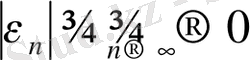 шығады [1] .
шығады [1] .
Айталық, [a, b] кесіндісінде кез келген (n+1) тізбегінің x
0
, x
1
, …, x
n
түйіндері y = f(x) функциясында өзінің y
0
, y
1
, …, y
n
мәндерімен берілсін, мұндағы y
i
= f(x
i
) .
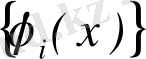 жүйесі ретінде
жүйесі ретінде
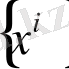 жүйесін таңдаймыз,
жүйесін таңдаймыз,
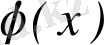 -ті
P
n
(
x
) арқылы белгілейміз, сонда алгебралық интерполяциялау есебі n дәрежелі
P
n
(
x
) =
a
0
x
n
+
a
1
x
n-1
+ +… +
a
n
көпмүшелілігін құруда
-ті
P
n
(
x
) арқылы белгілейміз, сонда алгебралық интерполяциялау есебі n дәрежелі
P
n
(
x
) =
a
0
x
n
+
a
1
x
n-1
+ +… +
a
n
көпмүшелілігін құруда
Интерполяция шартын қанағаттандыратын (19) теңдеуін алуда болып табылады.
Біріншіден, (19) теңдеудің шарты негізінде n дәрежелі жалғыз P n ( x ) полиномын құруды дәлелдейміз. Егер оның барлық a i ( i = 0, 1, 2, . . . , n ) коэффициенттері анықталған болса, онда P n ( x ) полиномы табылған деп есептелінеді.
1-теорема. Айталық, x 0 , x 1 , . . . , x n әртүрлі нүктелерінде y 0 , y 1 , …, y n сандары берілсін, сонда P n ( x i ) = y i , i = 0, 1, 2, …, n шартын қанағаттандыратын n дәрежеден аспайтын Р n ( х ) жалғыз полиномы бар болады.
Дәлелденуі. P n ( x ) полиномын құру үшін a i ( i = 0, 1, 2, . . . , n ) коэффициенттерін анықтаймыз. . a i ( i = 0, 1, 2, . . . , n ) коэффициенттерін P n ( x ) полиномы (5. 1) шартын қанағаттандыратындай таңдаймыз. Сонда келесі түрдегі (n+1) теңдігін аламыз.
Бұл теңдіктер бірдей емес алгебралық (n+1) жүйелерінің (n+1) a 0 , a 1 , . . . , a n белгісіздерімен жиынтығын береді. Жүйенің анықтауышы

 функция жүйесінің Вандермонд анықтауышы болып табылады. Шарт бойынша
x
i
(
i
= 0, 1, . . . ,
n
) арасында сәйкестік болмаса, онда
функция жүйесінің Вандермонд анықтауышы болып табылады. Шарт бойынша
x
i
(
i
= 0, 1, . . . ,
n
) арасында сәйкестік болмаса, онда
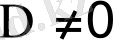 болады және (5. 2) жүйесі кез келген
y
i
,
i
= 0, 1, 2, . . . ,
n-де a
0
*
,
a
1
*
,
. . .
,
a
n
*
және бұл шешім жалғыз.
болады және (5. 2) жүйесі кез келген
y
i
,
i
= 0, 1, 2, . . . ,
n-де a
0
*
,
a
1
*
,
. . .
,
a
n
*
және бұл шешім жалғыз.
Егер a 0 * , a 1 * , . . . , a n * шешімінде P n ( x ) полиномының коэффициенттерін алсақ, теорема толық дәлелденген болады [2] .
x 0 , x 1 , …, x n нүктелері интерполяциялық түйіндер деп, ал P n ( x) полиномы - интерполяциялық полином деп аталады. Интерполяциялық полиномды құрудың кейбір әдістерін қарастырайық.
2. 1 Лагранж түріндегі интерполяциялық полиномМына түрдегі интерполяциялық полиномды іздейміз
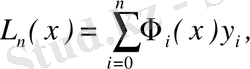
мұндағы, Ф i ( x ) - төмендегі шартты қанағаттандыратын, n дәрежелі полином
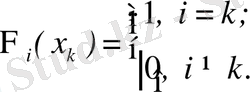
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz