Графтар теориясы және оның элементтері

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым Министрлігі

Семей қаласындағы Шәкәрім атындағы Мемлекеттік Университеті

СОӨЖ

Тақырыбы: Графтар теориясы және оның элементтері

Орындаған:Садырбаева Б. С.

Тексерген:Джунусова М. Ж.

Семей 2015 жыл

Графтар теориясы (ағылш. graph theory ) - түйіндері нүктелер жиыны, ал түйіндердің жалғасуы (қабырға деп аталатын) парлы екі нүкте болып келетін тор түрінде бейнеленеді. Егер түйіндердің жалғасу реті айтарлықтай маңызды болса - бағытталған граф, әйтпесе бағытталмаған граф болады. Графтар информатикада кеңінен қолданылады, айталық, алгоритмдер схемасы немесе программалар бағытталған графтарға жатады.

Түрлері

Бағдарланбaғaн граф (Неориентированный граф) - төбелерді қосатын доғаларының бағыты болмайтын граф.
Бағдарланған граф (Ориентированный граф; directed graph) - әр түрлі төбелер жұбын жалғастыратын қабырғалармен бірге түйіндердің (немесе төбелердің) құр ақырғы жиыны. Егер е қабырғасы Vl және V2 төбелерін жалғастырса, онда Vl мен И, -ні инцидент деп атайды және бұл төбелер көршілес болып саналады, е - реттелмеген жұп (К, и V2) . Әдетте, граф көрнекті формада ұсынылады, сонымен бірге төбелері нүктелермен немесе кейде ұқсастыру мақсатымен ентаңбаланған басқа мүсіндермен, ал қабырғалары сәйкес нүктелерді жалғастыратын сызықтармен кескінделеді. Егер әрбір қабырғаға бағыт көрсетілсе, онда мұндай граф бағдарланған граф деп аталады. Бұл жағдайда қабырға әр түрлі төбелердің реттелген жұбының жиынын үйымдастырады және оларды көбінесе доға деп атайды. Бағдарланған граф көрнекті түрде ұсынылған кезде әрбір доға жебелікпен жабдықталады.

Көптеген қолданбалы есептерде айналамызды қоршаған ортаның әртүрлі объектілер арасындағы байланыстар жүйесі зерттеледі. Объектілер төбелер деп аталып, нүктелер арқылы белгіленеді, ал төбелер арасындағы байланыстар доғалар деп аталып, сәйкес нүктелерді қосатын бағытталған түзулермен белгіленеді. Қала көшелерін граф арқылы кескіндеуге болады: көше қиылысуларын графтардың төбесі деп, ал көшелерді доғалар деп алуға болады;

Блок-схемаларды да граф түрінде кескіндеуге болады: блоктар - граф төбелері, ал операцияның орындалу кезегін көрсететін стрелкалар доғалар.

Анықтама: G=(M, R) алгебралық жүйе граф деп аталады. Мұндағы М-жиынтығы бос емес жиын, оның элементтері графтың төбелері деп аталады, ал бинарлы R қатынасының R M ² элементтері доғалар деп аталады. Сонымен граф төбелері дегеніміз -айналамызды қоршаған ортаның кез келген объектісі. Олардың саны шектеулі болғандықтан, біз оларды натурал сандармен белгілейміз. Ал граф қабырғалары оның кейбір төбелерін қосады. Граф қабырғаларын әдетте латын әріптерімен белгілейді. G= ‹M, R› графының геометриялық кескіні жазықтықта графтың әр төбесін нүкте арқылы белгілеп, егер (a, b) R болса а төбесінен b төбесіне доға жүргізу арқылы алынады. Мысалы: төбелері М={1, 2, 3, 4}, ал доғалары R={(1, 1), (1, 2), (2, 3), (3, 4), (4, 3), (4, 1) } болатын G графының геометриялық кескіні төмендегідей:

Графтың төбелерінің қандай сызықтарымен қосылатындығы (түзу әлде қисық), сызықтардың ұзындығы туралы ақпараттар маңызды емес. Төбелердің арасында байланыс бар екендігі және ол байланыс туралы ақпарат R доғалар жиынында екендігі болса болды. Төбелерді қосатын сызықтардың бағыты көрсетілген болуы мүмкін (мысалдағы сияқты) . Мұндай граф бағытталған граф деп аталады (оргграф) . Оған математикалық түрде мынандай анықтама беруге болады.

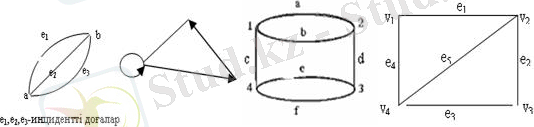
Анықтама : Егер R қатынасы симметриялы болмаса, яғни (a, b) R, (b, а) R онда G=<M, R> графы бағытталған (оргграф) деп аталады, ал R қатынасы симметриялы болса (a, b) R, (b, а) R онда G бағытталмаған (неоргграф) немесе н-граф деп аталады Айталық: a, b-граф төбелері, e=(a, b) оларды қосатын доға болсын. Мұндай жағдайда а , b төбелері мен е доғасы инцидентті деп аталады. b мен e доғасы даинцидентті. Әр доға e E өзі қосатын екі төбеге инцидентті болады. Бір доғамен қосылатын 2 төбе сыбайлас ( бүйірлес) деп аталады.

Анықтама: Төбелердің бір жұбына инцидентті доғалар еселі немесе параллель доғалар деп аталады

Анықтама: Еселі доғалары бар граф мультиграф деп аталады.

Анықтама: Шығатын және кіретін төбесі біреу болатын доға ілгек деп аталады.

Анықтама : Егер (a, b), (b, а) доғалары бір уақытта R қатынасына жатса, онда бұл доғалар туралы ақпаратты [a, b] = {(a, b), (b, a) } жиыны арқылы көрсетуге болады. [a, b] жиыны қабырға деп аталады.

Мысалы, мына суреттегі графтың 4 төбесі, 5 қабырғасы бар.

Төбелері: v ₁ , v ₂ , v ₃ , v ₄ ; Қабырғалары:e ₁ , e ₂ , e ₃ , e ₄ e ₅ ; Бұл графтағы v ₁ мен v ₂ ; v ₂ мен v ₃ ; v ₃ пен v ₄ ; v ₄ пен v ₅ іргелес төбелер, v ₁ , v ₃ -сыбайлас емес.

Сол сияқты: e ₁ , e ₂ ; e ₂ , e ₃ ; e ₃ , e ₄ ; e ₄ , e ₁ ; e ₁ , e ₅ ; e ₂ , e ₅ ; e ₃ , e ₅ ; e ₄ , e ₅ ; -қабырғалары сыбайлас. e ₁ , e ₃ ; e ₂ , e ₄ ; - сыбайлас емес қабырғалар.

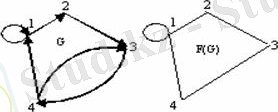
Егер G={M, R} орграфындағы әр (a, b) R доғасына, (b, a) жұбын қосса нәтижесінде берілген G графына сәйкес Н-граф шығады, оны F(G) деп белгілейді.

Анықтама : Егер граф элементтерінің (төбелері мен қабырғалары) жиыны ақырлы болса, графта ақырлы деп, ал қабырғалар жиыны бос болса, бос граф деп аталады.

Ілгексіз, әрі еселі қабырғалары жоқ және әрбір төбелер жұбы қабырғамен қосылған граф толық граф деп аталады.

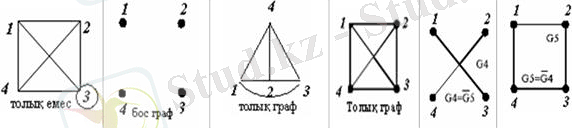
Анықтама : Берілген G графындағыдай төбелері және G графына қосқанда оны толық