Элементар электр заряды және электростатикалық өріс: Кулон заңы, Гаусс теоремасы, диэлектрлік өтімділік және конденсаторлар


Қазақстан Республикасының Білім және Ғылым министрлігі Семей қаласының Шәкәрім атындағы мемлекеттік университеті
Жаратылыстану-математика факультеті
Физика мамандығы
СӨЖ
Тақырыбы: Элементар электр зарядың анықтау. 2. Кулон заңының әртүрлі қашықтықтар үшін тәжірибе жүзінде тексерілуі. Кавендиш әдісі. 3. Вакуумдағы кейбір электростатикалық өрістерге Гаусс теоремасын қолдану. 4. Эквипотенциал беттер. 5. Электрлік ығысу векторы және диэлектрлік өтімділік. 6. Конденсаторлар, олардың түрлері және сиымдылықтары
Топ: T-423
Орындаған: Берікова Е.
Тексерген: Рахимбердина А. Т.
Семей 2015 жыл
Электр зарядының сақталу заңы.
Электр зарядының бар болуы зарядталған денелердің басқадай денелермен өз ара әсерлесетіндігінен көрінеді.
Шартты түрде оң және теріс деп аталатын екі түрлі электр заряды бар. Бірдей таңбалы зарядтар бір - бірінен тебіледі, әртүлі таңбалылары тартылады.
Элементар бөлшектердің барлығының да заряды (егер ол нольге тең болмаса) абсолют шамасы бойынша бірдей болады. Оны
элементар заряд
деп атауға болады. Біз оны
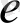 әрпімен белгілейміз. Кулонмен өрнектелген элементар заряд мынаған тең:
әрпімен белгілейміз. Кулонмен өрнектелген элементар заряд мынаған тең:
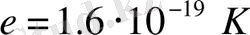 . Егер әйтеуір бір себеппен (мысалы, үйкеу арқылы) денеде бір таңбалы бөлшектердің артық санын туғызсақ (осыған сәйкес мұнда екінші таңбалы бөлшек жетіспейтін болады), онда дене зарядталған болады.
. Егер әйтеуір бір себеппен (мысалы, үйкеу арқылы) денеде бір таңбалы бөлшектердің артық санын туғызсақ (осыған сәйкес мұнда екінші таңбалы бөлшек жетіспейтін болады), онда дене зарядталған болады.
Электр зарядтарының жоғалуы және қайтадан пайда болуы мүмкін. Алайда әрқашан қарама-қарсы таңбалы екі элементар заряд бір мезгілде жоғалып немесе пайда болып отырады. Сондықтан электрлік изоляцияланған жүйе зарядтарының қосындысы өзгеруі мүмкін емес. Бұл тұжырымдау электр зарядының сақталу заңы деп аталады.
Кулон заңы.
Бірдей таңбалы зарядтарды (немесе аттас зарядталған деп аталатын) тасушы денелер бірін-бірі тебеді. Ал, әр аттас зарядты денелер бірін-бірі тартады. Нүктелік деп аталатын зарядтардың өз ара әсер күші бағынатын заңды 1785 жылы Кулон анықтаған.
Нүктелік заряд - электрленген материялық нүкте. Нүктелік заряд деп осы дененің электр зарядтарын тасымалдайтын басқа денелерге дейінгі қашықтығымен салыстырғанда мөлшерін ескермеуге болатын зарядталған денені айтады.
Кулон заңы былай тұжырымдалады: нүктелік екі зарядтың өз ара әсер күші әрбір зарядтардың шамаларына пропорционал және олардың ара қашықтығының квадратына кері пропорционал . Кулон заңы мына формуламен өрнектеледі:
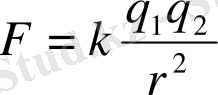 .
.
мұндағы:
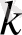 - пропорционалдық коэффициент,
- пропорционалдық коэффициент,
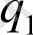 мен
мен
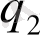 өз ара әсерлесетін зарядтардың шамалары,
өз ара әсерлесетін зарядтардың шамалары,
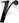 - олардың ара қашықтығы.
- олардың ара қашықтығы.
СИ системасында зарядтың бірлігі Кулон (К) болып табылады.
Кулон заңындағы пропорционалдық коэффициентті
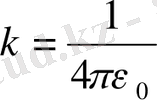 - ге тең деп алады.
- ге тең деп алады.
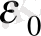 - шамасы
электрлік тұрақты
деп аталады. Ол мынаған тең:
- шамасы
электрлік тұрақты
деп аталады. Ол мынаған тең:
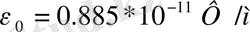 . Оның өлшеуіштігі электр сиымдылығын ұзындықққа бөлгенге тең. Осыған сәйкес оның бірліктерін
фарад бөлінген метр
деп өрнектейді.
. Оның өлшеуіштігі электр сиымдылығын ұзындықққа бөлгенге тең. Осыған сәйкес оның бірліктерін
фарад бөлінген метр
деп өрнектейді.
Егер әсерлесуші зарядтар изотропты ортада болса, онда Кулон күші мынаған тең: F =
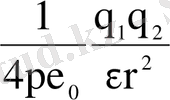 ; Мұндағы:
; Мұндағы:
 - ортаның диэлектрлік өтімділігі. Вакуумның диэлектрлік өтімділігі
- ортаның диэлектрлік өтімділігі. Вакуумның диэлектрлік өтімділігі
 =1.
=1.
Электр зарядының көлемдік тығыздығы - ρ=
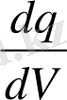 ;
;
Электр зарядының беттік тығыздығы - σ=
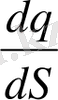 ;
;
Электр зарядының сызықтық тығыздығы -
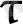 =
=
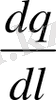 ;
;
Егер жүйе сыртқы ортамен ешбір электр зарядтарымен алмаспаса, ондай жүйені - оқшауланған электр жүйесі дап атайды. Оқшауланған электр жүйесі үшін электр зарядының сақталу заңы орындалады.
Кез-келген тұйықталған жүйеде электр зарядтарының алгебралық қосындысы әр уақытта өзгеріссіз қалып отырады, яғни
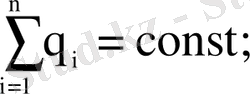
Оқшаулаған жүйені құрайтын зарядталған денелер немесе бөлшектердің алгебралық қосындысы барлық процестерде өзгермейді.
Электростатикалық өріс. Электр өрісінің кернеулігі.
Электр өрісі - электр зарядтары өзара әсерлесетін материяның түрі. Электр өрісін заряд туғызады. Қозғалмайтын заряд өрісін - электростатикалық деп атайды. Элекр өрісін өлшеуіш құралдармен байқауға болады. Осы сыншы зарядты электр өрісіне қойған кезде оң зарядтардың кеңістіктегі орнына және мәніне ешбір өзгеріс енгізбеу керек. Осыған қандайда бір F күші әсер етсін делік. Осы күштің сынақ зарядқа қатынасының векторлық шамасы электр өрісінің кернеулігі деп аталды.
Зарядтардың арасындағы әсер электр өрісі арқылы жүзеге асырылады. Кез-келген заряд өзінің айналасында кеңістіктің қасиетін өзгертеді - онда электр өрісін туғызады. Берілген жерде өрістің барын анықтау үщін ол жерге зарядталған денені орналастырып, ол электр күштерінің әсерін байқай ма жоқ па соны анықтаймыз.
Сөйтіп, электр өрісін біліп, зерттеу үшін белгілі бір “сынақ” зарядты пайдалану керек.
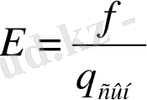 - бұл векторлық шаманы берілген нүктедегі (яғни сынақ
- бұл векторлық шаманы берілген нүктедегі (яғни сынақ
 зарядтың
f
күштің әсеріне ұшырайтын нүктедегі)
электр өрісінің кернеулігі
деп атайды.
зарядтың
f
күштің әсеріне ұшырайтын нүктедегі)
электр өрісінің кернеулігі
деп атайды.
Электр өрісінің кернеулігінің өлшем бірлігі: Ньютон бөлінген Кулон (Н/Кл) .
Өрістердің суперпозициясы. Диполь өрісі.
Электр өрісінің суперпозиция (беттесу) принципі
былай тұжырымдалады: Зарядтар системасының өріс кернеулігі системаның әрбір зарядтары жеке-жеке туғызатын өріс кернеуліктерінің векторлық қосындысына тең:
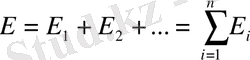
Бұл өрнек электростатикалық өрістің суперпозиция принципі деп аталады.
Электрлік диполь деп шамалары жағынан тең, система өрісі анықталатын нүктеге қарағанда ара қашықтығы l едәуір аз әр текті екі, +q және -q нүктелік зарядтан құрылған жүйені айтамыз.
q
-

 q
+
q
+
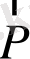
- + (1-сурет)
Зарядтардың екеуі арқылы өтетін түзу дипольдің осі деп аталады.
Кез келген нүктедегі дипольдің өріс кернеулігі мынадай формула арқылы анықталады:
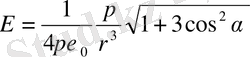
Мұндағы
 - дипольдің осі мен берілген нүкте бағытының арасындағы бұрыш.
- дипольдің осі мен берілген нүкте бағытының арасындағы бұрыш.
Диполь моменті деп - оң зарядтар шамасының зарядтар ара қашықтығына көбейтіндісін және диполь иінінің бағытымен бағыттас векторды айтады:
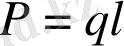
Диполь өрісінің кернеулігінің формуласы:
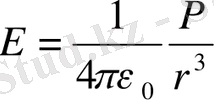 .
.
Кернеулік векторының ағыны.
Кернеулік сызығының ағыны
- скалярлы шама. Сонымен,
кернеулік ағыны
деп - белгілі бір бет арқылы өтетін күш сызықтарының санын айтады.
Е
сызықтарының жиілігі
Е
-
нің сан мәніне тең болатындай етіп таңдап алынатындықтан,
Е
векторына перпендикуляр
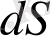 ауданшаны тесіп өтетін сызықтар саны сан жағынан
Е
ауданшаны тесіп өтетін сызықтар саны сан жағынан
Е
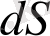 -
ке тең болады. Егер
-
ке тең болады. Егер
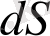 ауданшасы оған түсірілген нормаль
Е
векторымен
ауданшасы оған түсірілген нормаль
Е
векторымен
 бұрышын жасайтындай етіп бағдарланған болса, онда ауданшаны тесіп өтетін сызықтар саны сан жағынан мынаған тең болады:
Е
бұрышын жасайтындай етіп бағдарланған болса, онда ауданшаны тесіп өтетін сызықтар саны сан жағынан мынаған тең болады:
Е
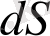
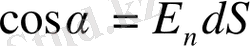 . Мұндағы
. Мұндағы
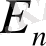 - ауданшаға түсірілген нормаль бойындағы
Е
вектордың құраушысы.
- ауданшаға түсірілген нормаль бойындағы
Е
вектордың құраушысы.
Е
(кернеулік) вектор ағыны мынаған тең:
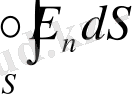 .
.
Гаусс теоремасы.
Кез келген
r
радиусты сфералық бетті қиып өтетін сызықтардың толық саны N сызықтар жиілігі мен сфералық бет ауданының
 көбейтіндісіне тең болады. Шарт бойынша сызықтар жиілігі сан жағынан
көбейтіндісіне тең болады. Шарт бойынша сызықтар жиілігі сан жағынан
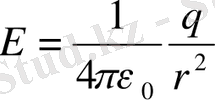 шамасына тең. Демек, N шамасы сан жағынан мынаған тең:
шамасына тең. Демек, N шамасы сан жағынан мынаған тең:
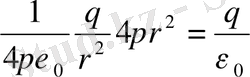 ,
,
яғни зарядтан кез келген қашықтықтағы сызық саны бірдей болады.
Е
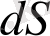
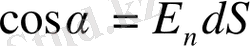 өрнегіне сәйкес қандай да бір бет арқылы өтетін
Е
вектор ағыны сан жағынан осы бетті қиып өтетін
Е
сызық санына тең болады. Демек, зарядты қоршаған сфералық бет арқылы өткен
Е
вектор ағыны
өрнегіне сәйкес қандай да бір бет арқылы өтетін
Е
вектор ағыны сан жағынан осы бетті қиып өтетін
Е
сызық санына тең болады. Демек, зарядты қоршаған сфералық бет арқылы өткен
Е
вектор ағыны
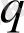 /
/
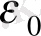 - ге тең. Ағынның таңбасына дәл келеді. Егер бет тұйықталған және оның ішінде
q
заряд бар болса, кез келген басқа формалы бет үшін де
Е
вектор ағыны
- ге тең. Ағынның таңбасына дәл келеді. Егер бет тұйықталған және оның ішінде
q
заряд бар болса, кез келген басқа формалы бет үшін де
Е
вектор ағыны
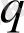 /
/
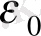 болады.
болады.
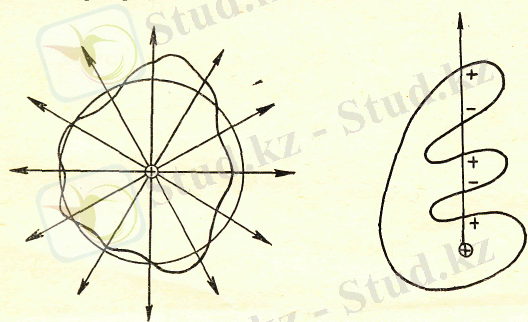
Оны мына суреттен көруге болады:
 (а) (б)
(а) (б)
2 - сурет.
“Әжімі” (“қыртысы”) жоқ бет үшін бұл тұжырым өзінен-өзі айқын. Шынында, мұндай бет сфералық бет сияқты. Әрбір
Е
сызығымен бір-бір реттен қиылысады. Сондықтан қиылысу саны зарядтан шығатын сызықтардың санына, яғни
 /
/
 -ге тең.
-ге тең.
“Әжімі” бар бет арқылы өтетін ағынды есептеуде (
 /
/
 санды
Е
сызығының біреуі ғана көрсетілген 2 б-сурет), берілген
Е
сызығының қиылысу саны қарастырылып отырған жағдай үшін тек қана тақ болатындығын, сонымен бірге бұл қиылысулар жалпы ағынға бірде оң, бірде теріс үлесін алма-кезек қосып отыратындығын ескеру керек. Нәтижесінде берілген сызық қанша рет қиып өтпесін, ағынға қосылатын қорытынды үлес не плюс бірге (ақырында сыртқа шығатын сызықтар үшін) не минус бірге (ішке кіретін сызықтар үшін) тең болады.
санды
Е
сызығының біреуі ғана көрсетілген 2 б-сурет), берілген
Е
сызығының қиылысу саны қарастырылып отырған жағдай үшін тек қана тақ болатындығын, сонымен бірге бұл қиылысулар жалпы ағынға бірде оң, бірде теріс үлесін алма-кезек қосып отыратындығын ескеру керек. Нәтижесінде берілген сызық қанша рет қиып өтпесін, ағынға қосылатын қорытынды үлес не плюс бірге (ақырында сыртқа шығатын сызықтар үшін) не минус бірге (ішке кіретін сызықтар үшін) тең болады.
Гаусс теоремасының тұжырымдамасы
: тұйықталған бет арқылы өтетін электр өрісі кернеулігінің вектор ағыны осы беттің ішінде жатқан зарядтардың алгебралық қосындысын
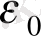 - ге бөлгенге тең.
- ге бөлгенге тең.
Гаусс теоремасы былай өрнектеледі:
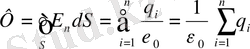 .
.
Электр өрісінің кернеулік сызықтары. Электрлік ығысу.

3 (а) - сурет.
+ + + +
- - 3 (б) - сурет.
Электр өрісі кернеулігін сызықтармен кескіндейді. Ол сызықтардың әр нүктесіндегі жанамалар, сол нүктедегі өрістің кернеулігі (
 ) векторымен дәл келетін болу керек. Мұндай сызықтар өрістің
күш сызықтары
немесе
кернеулік сызықтары
деп аталады (3 а - сурет) .
) векторымен дәл келетін болу керек. Мұндай сызықтар өрістің
күш сызықтары
немесе
кернеулік сызықтары
деп аталады (3 а - сурет) .
Күш сызықтары оң зарядтардан басталып, теріс зарядтарда немесе шексіздікте аяқталады.
Шамалары бірдей және қарама-қарсы зарядтары бар жазық екі пластинка ара сындағы өрісті кескіндейік. Барлық нүктелердегі кернеулігінің шамасы мен бағыты бірдей болатын өріс біртекті өріс деп аталады. Біртекті өрістің күш сызықтары бір-бірінен бірдей қашықтықта жататын параллель түзулер. 3 б-суретте әр аттас зарядталған екі пластинка арасындағы кернеулік сызықтары бірдей өріспен көрсетілген.
Электрлік ығысу векторы
сан жағынан кернеулік векторы
Е
-нің абсолюттік диэлектрлік өтімділікке (
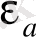 ) көбейтіндісіне тең болады:
) көбейтіндісіне тең болады:
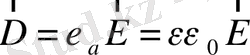 ; ал скаляр түрде
; ал скаляр түрде
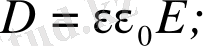
Электрлік ығысу Кл/м 2 - пен өлшенеді. Берілген бір бетті тесіп өтетін электрлік ығысу саны электрлік ығысу векторының ағыны деп аталады.
Кез-келген әртекті өрісте белгілі бір S бетті тесіп өтетін электрлік ығысу ағыны:
Ф=
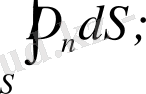
Электростатикалық өріс күштерінің жұмысы. Потенциал .
Электростатикалық өріс (яғни қозғалмайтын зарядтар туғызатын) күштерінің потенциалдығына тікелей көз жеткізейік. Бұл үшін қозғалмайтын нүктелік
q
зарядтың өрісіндегі күштердің осы өрістегі
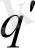 нүктелік зарядтың орын ауыстыруда істеген жұмысын есептейік. Сонда элементар
dl
жолдағы істелген жұмыс мынаған тең:
нүктелік зарядтың орын ауыстыруда істеген жұмысын есептейік. Сонда элементар
dl
жолдағы істелген жұмыс мынаған тең:
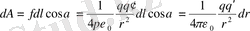
мұндағы,
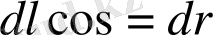 . Бұдан
1-2 жолдағы
жұмыс
үшін мынадай өрнек шығады:
. Бұдан
1-2 жолдағы
жұмыс
үшін мынадай өрнек шығады:
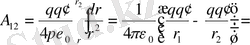
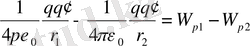
Осыдан
q
зарядтың өрісіндегі
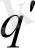 зарядтың
потенциалдық энергиясы
:
зарядтың
потенциалдық энергиясы
:
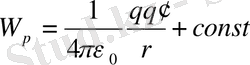 .
.
Өрістің берілген нүктесіндегі түрліше сынақ зарядтардың
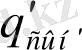
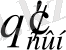 т. б. энергиялары түрліше
т. б. энергиялары түрліше
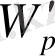 ,
,
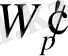 т. б. болады. Алайда,
т. б. болады. Алайда,
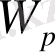 /
q
/
q
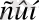 қатынасы барлық зарядтар үшін бірдей болады:
қатынасы барлық зарядтар үшін бірдей болады:
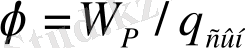
Нүктелік заряд өрістің потенциалы:
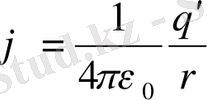
Потенциалы
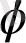 болатын өрістің нүктесіндегі зарядтың потенциалдық энергиясы
:
болатын өрістің нүктесіндегі зарядтың потенциалдық энергиясы
:
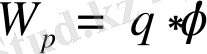
Өріс күштерінің зарядқа істеген жұмысы
заряд шамасын бастапқы және ақырғы нүктелердегі потенциалдар айырмасына көбейткенге тең
:
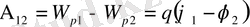
Егер
q
заряды потенциалы
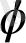 болып келген нүктеден шексіздікке қашықтатылса (потенциалы нөлге тең жерде), өріс күшінің жұмысы мынаған тең:
болып келген нүктеден шексіздікке қашықтатылса (потенциалы нөлге тең жерде), өріс күшінің жұмысы мынаған тең:
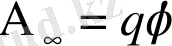 Потенциалдың вольт (
В
) деп аталатын
СИ
бірлігі үшін 1 кулонға тең зарядты шексіздіктен осындай нүктеге алып келгенде
1дж
жұмыс істеу қажет болатын потенциалы алынады:
1дж=1к*1 В
бұдан
1 В
=
Потенциалдың вольт (
В
) деп аталатын
СИ
бірлігі үшін 1 кулонға тең зарядты шексіздіктен осындай нүктеге алып келгенде
1дж
жұмыс істеу қажет болатын потенциалы алынады:
1дж=1к*1 В
бұдан
1 В
=
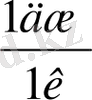 .
.
1эв=1. 60*10 -19 к*1в=1. 60*10 -19 дж=1. 60*10 -12 эрг
Сондай-ақ электронвольтке еселік бірліктер пайдаланылады:
1кэв(килоэлектронвольт) =10 3 эв
1мэв(мегаэлектронвольт) =10 6 эв
1гэв(гигаэлектронвольт) =10
9
эв
Электр өрісі кернеулігі мен потенциал арасындағы байланыс.
Электр өрісін не векторлық шама
Е
арқылы, не скаляр шама
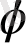 арқылы сипаттауға болады. Шынында, өріс күштерінің
q
арқылы сипаттауға болады. Шынында, өріс күштерінің
q
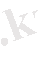 зарядқа
зарядқа
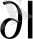 жол кесіндісіне істеген жұмысы бір жағынан
q
жол кесіндісіне істеген жұмысы бір жағынан
q
 ,
екінші жағынан зарядтың потенциялық энергиясының кемуі түрінде, яғни
-d(q
,
екінші жағынан зарядтың потенциялық энергиясының кемуі түрінде, яғни
-d(q
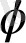 )
=-
q
)
=-
q
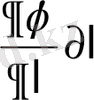 түрінде көрсетілуі мүмкін. Бұл өрнектерді теңестіру ақылы мынаны аламыз:
түрінде көрсетілуі мүмкін. Бұл өрнектерді теңестіру ақылы мынаны аламыз:
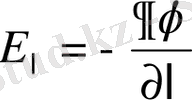 .
.
мұндағы
 арқылы кеңістікте еркін таңдап алынған бағыт белгіленген. Дербес жағдайда,
арқылы кеңістікте еркін таңдап алынған бағыт белгіленген. Дербес жағдайда,
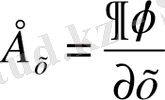 ,
,
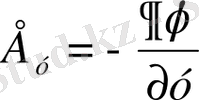 ,
,
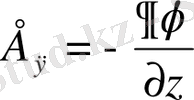 .
.
Осыдан:
Е=i
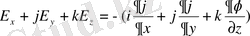
Жақшаның ішіндегі өрнек
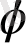 скалярдың градиенті
(
grad
скалярдың градиенті
(
grad
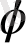 ) деп аталады.
) деп аталады.
Градиенттің белгілеуін пайдаланып, былай жазуға болады:
Е=-grad
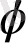 .
.
Сөйтіп, электр өрісінің кернеулігі кері таңбамен алынған потенциалдың градиентіне тең.
Эквипотенциал беттер.
Өрісті көрнекті кескіндеу үшін кернеуліктер сызығының орнына потенциалдары бірдей беттерді немесе эквипотенциал беттерді пайдалануға болады. Атының өзі айтып тұрғандай, эквипотенциал бет-бұл барлық нүктелерінің потенциалы бірдей бет. Егер бет х, у, z функциясы түрінде берілсе, онда эквипотенциал беттің теңдеуі мына түрде болады:
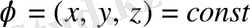
Эквипотенциал бетке жүргізілген нормальдің бағыты сол нүктедегі Е векторының бағытымен дәл келеді.
Эквипотенциал бетті өрістің кез келген нүктесі арқылы жүргізуге болады.
Диэлектриктердегі электр өрісі. Полярлы және полярлы емес молекулалар.
Диэлектриктер - электр өткізбейтін заттар оң зарядтар мен теріс зарядтары тең мөлшерде болып келетін молекулалардан немесе диэлектрик ішінде емін еркін қозғала алмайтын иондардан тұрады.
Сыртқы электр өрісі болмаған кезде оң және теріс зарядтардың ауырлық центрлері бір-біріне қатысты дәл келуі де немесе ығысқан болуы да мүмкін. Соңғы жағдайда молекула электр дипольге эквивалентті болады да
полярлық деп
аталады. Полярлық молекуланың меншікті электрлік моменті:
Р=ql
. Өлшем бірлігі:
 .
.
Өріс жоқ болғанда әр таңбалы зарядтардың ауырлық центрлері біріккен, меншікті электрлік моменттерге ие болмайтын молекулалар
полюссіз
деп аталады. Сыртқы электр өрісінің әсерінен полюссіз молекулалардағы зарядтар бір-бірімен салыстырғанда оң зардтар өріс бағытымен, терістері өріске қарсы ығысады. Рационалданған системада пропорционалдық коэффицентті
 түрінде жазамыз, мұндағы
түрінде жазамыз, мұндағы
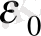 -электрлік тұрақты, ал
-электрлік тұрақты, ал
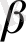 -молекуланың полюстену қабілеті.
p
мен
E
бағыттары дәл келетіндігін ескере отырып былай жазуға болады:
Р
=
-молекуланың полюстену қабілеті.
p
мен
E
бағыттары дәл келетіндігін ескере отырып былай жазуға болады:
Р
=
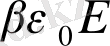 .
.
Полюсті емес молекуланың полюстену процесі молекуланың оң және теріс зарядтары өз ара серпімді күштермен байланысқандағыдай болады. Сондықтан полюсті емес молекула сыртқы өрісте өзін серпімді диполь сияқты көрсетеді.
Полюстік молекулаға сыртқы өрістің әсері негізінде молекуланы оның электрлік моменті өріс бағыты бойынша орналасатындай бұруға тырысады. Электрлік моменттің шамасына сыртқы өріс іс жүзінде әсер етпейді. Демек, полюстік молекула сыртқы өрісте өзін қатаң диполь ретінде ұстайды.
Дипольдің моменті
мынаған тең
:
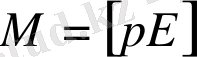 .
.
Диэлектриктердің поляризациялануы.
Сыртқы өрістің әсерінен диэлектрик поляризацияланады. Мүның өзі диэлектриктің қорытқы электрлік моменті нольден өзгеше болады деген сөз.
Егер өріс немесе диэлектрик біртекті болмаса, диэлектриктің түрліше нүктелеріндегі поляризациялану дәрежесі әр түрлі болады. Берілген нүктедегі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz