Ең кіші квадраттар әдісінің мағынасы

Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ

СЕМЕЙ ҚАЛАСЫНЫҢ ШӘКӘРІМ АТЫНДАҒЫ МЕМЛЕКЕТТІК УНИВЕРСИТЕТІ

ОӨЖ

Ең кіші квадраттар

әдісінің мағынасы

Орындаған: Қадырова Ж. Р.

Тобы: УА-303

Тексерген: Жаксыгулова Д. Д

Семей 2015 жыл

Жоспар

Кіріспе

Негізгі бөлім

Ең кіші квадраттар әдісінің мәні
Ең кіші квадраттар әдісі бойынша регрессия

Қорытынды

Пайдаланылған әдебиеттер тізімі

Ең кіші квадраттар әдісінің мәні

Ең кіші квадраттар әдісі - қателер теориясының белгісіз шамаларды кездейсоқ қателері бар өлшеулердің нәтижесін бағалау үшін қолданатын әдістерінің бірі. Ең кіші квадраттар әдісі берілген функцияларды олардан гөрі қарапайым функциялар арқылы жуықтап өрнектеу үшін де пайдаланылады. Бұл әдісті 1794 - 95 ж. ‘’К. Гаусс’’ және 1805 - 06 ж. француз математигі ‘’А. Лежандр’’ (1875 - 1961) ұсынған. Ең кіші квадраттар әдісі алғашқыда астрономия және геодезия бақылаулардың нәтижесін өңдеу үшін қолданылды. Бірақ оның дәл математикалық негіздемесін жасап, қолданылу шекарасын көрсетіп берген орыс ғалымдары А. А. Марков (1856 - 1922) пен А. Н. Колмогоров болды.

Ең кіші квадраттар әдісі - математикалық статистиканың аса маңызды бір бөлімі және ол статистика қорытынды жасау үшін ғылым мен техниканың әр түрлі саласында кеңінен қолданылады. Гаусс бойынша, Ең кіші квадраттар әдісінің мәні - физикалық шаманың (μ) дәл мәнін (белгісіз) оның бақылаулар нәтижесінде есептелген жуық мәнімен (Х) ауыстырғандағы “шығын”, (X-μ) 2 қателік квадратына пропорционал болады деген пайымдауға негізделген. Мұндай жағдайда, “шығынының” орташа мәні ең кіші болатындай Х шамасының жүйелі қатесін тиімді баға деп есептеуге болады. Міне, осы талап Ең кіші квадраттар әдісінің негізіне алынады. Ал, жалпы жағдайда, Х шамасының Ең кіші квадраттар әдісі мағынасындағы тиімді бағасын іздеу күрделі есеп. Сондықтан практикада бұл есептің ауқымын тарылта отырып, Х ретінде бақылаулар нәтижесінен алынатын жүйелі қатесі болмайтын сызықтық функция таңдалады және ол функцияның барлық сызықтық функциялар класындағы “шығынының” орташа мәні ең кіші болуы тиіс. Егер бақылаулардың орташа қателері қалыпты үлестірілуге бағынса әрі бағаланатын шама (μ) бақылаулар нәтижесінің орташа мәндеріне сызықты тәуелді болса, онда мұндай есептің шешімі жалпы есептің де шешімі болады. Бұл жағдайда Х-тің тиімді бағасы да μ-дің орташа мәні бар қалыпты үлестірілуге бағынады.

ЕҢ КІШІ КВАДРАТТАР ӘДІСІ - Эконометриялық модель құру ерекшеліктері. Қандай модель болса да, құру үшін төмендегі шарттар орындалуы тиіс: - Зерттейтін процесстің мақсаты толық тұжырымдалады; - ең неізгі сапалық мінездемелері факторлары анықталады; - функционалдық, структуралық, құраушы элементтері анықталады; - элементтерінің арасындағы байланыстарға сөзбен сапалық саралау мен сипаттау жасалады; - дәл, қысқа, компакты түрде математикалық модель құрастырылады; - модельдің шешімі алынып, жан-жақты анализ (адекваттығынан бастап, қорытындысы арқылы болжам) жасалады. Осылайша құрылған эконометриялық модель (ЭМ) экономикалық математикалық модельге (ЭММ), экономистер үшін математикаға (МЭ), экономикалық теорияға сүйенеді. Бірақ ЭММ модель құрғанмен оның экономикалық құбылысқа сәйкестігін немесе алшақтығын Математика мен Статистика арқылы ғана зерттей алады. Ал ЭТ арқылы эконометриялық зерттеуге тиесілі құбылыстың (экономикалық қана емес) ең дәл, жалпы заңдылықтарға сәйкестігін салыстырады. Алдын ала немесе қорытындылар арқылы болжам (прогноз) жасау, әлеуметтік, саяси, экономикалық ситуацияларды бақылап дұрыс бағыт нұсқау ЭМ үлесінде. Сондықтан да ЭМ-ға анықтаманы бір сөзбен бере қою мүмкін емес. Жалпы алғанда құбылыстарды зерттеуде ЭТ, ЭММ, МЭ пайдалана отырып, әсіресе МС әртүрлі құрама әдістері арқылы жан-жақты толық мағлұмат алу ЭМ-ның негізгі мақсаты. Экономикалық және басқа да құбылыстардың математикалық формализациясы функционалдық тәріздес заңдылыққа әкеледі. Бірақ, макроэкономикада бұл байланыс дұрыс қойылған (корректно) байланыс болмайды. Себебі ресурстардың структураларының арасындағы байланыстардың өзі әртүрлі болуы әбден мүмкін. Сондықтан ЭМ-да эндогендік параметрлерден (у және х) басқа, процесс кезінде әсері болатын экзогендік параметрлер еңгізіледі ( ) яғни есептеу кезінде пайда болуына байланысты ескерілетін параметр (регулирующий параметр) . Сонымен, ЭМ модель - ЭМ зерттеудің негізгі инструменті (құрал - жабдығы) .

Ең кіші квадраттар әдісі - Жиындық регрессия моделінде қос сызықтық регрессия үшін пайдаланылатын ең кіші квадраттар әдісінің жалпылама түрі қолданылады. Бағаланған жиындық сызықтық регрессия теңдеуі

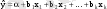
осындай теңдеуді барлық бақылаулар үшін жазайық

Бағаланған жиындық сызықтық регрессия теңдеуі матрицалық түрде былай жазылады

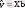
мұнда 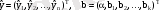-тік жолдар. Жоғары индекс әріпі транспонирленген матрица екенін көрсетеді. Тәуелді айнымалы тің нақты мәндері және оның теңдеуімен анықталған сәйкес мәндерінен ауытқуын анықтаймыз

Ең кіші квадраттар әдісі ауытқулардың квадраттарының қосындысының минимум шартынан (2) теңдеудің коэффициенттерін анықтауға негізделген

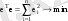
Матрицалардың қасиеттерін пайдаланып,

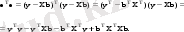
Х матрицасының тік жолдары сызықтық тәуелсіз болса, онда 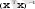кері матрица болады және регрессия теңдеуінің коэффициенті векторының бағасын келесі формула бойынша табуға болады.

2. Ең кіші квадраттар әдісі бойынша регрессия

Айталық, 4 бақылау болсын делік. Ең бірінші қадам әрбір бақылау үшін қалдықты табу керек. у-фактілі мән болса, есептеу мәні у деп белгіленеді. Ендеше қалдық 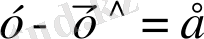деп белгіленеді. 4 бақылау болғандықтан, әр бақылау үшін қалдық деп белгіленеді. Осы қалдықтар min болатындай регрессия сызығын табуымыз қажеттілігі айдан анық. . Ендеше min болуы үшін қалдықтар квадраттарының қосындысы S

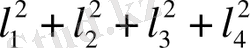
S шамасы а мен b - ға байланысты, өйткені олар регрессия сызығының орнын көрсетеді. S кіші болған сайын, сәйкестік қатаң. S=0 болса, онда абсолютті нақты сәйкестік алынады деген сөз, өйткені мұндай жағдайда барлық қалдық = 0 деген сөз.

Мысал 1. Айталық 2 бақылау берілсін. у=3, х=1 болғанда, у=5, х=2 болғанда: y=a+bx (1) теңдеуінің а және b коэффициентін бағалаймыз. Екі бақылау болғандықтан екі нүкте арқылы регрессия сызығын жүргізе отырып нақты сәйкестікті ала аламыз. Егер х=1 болса, у=а+в х=2 болса у=а+2в.

х:

у:

а+ b

а+2в

Е:

3-а- b

5-а-2 b

Бұдан 1-ші бақылаудың қалдығы 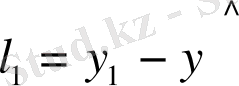=3-а- b, 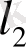=5-а-2b Ендеше

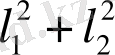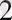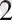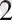S= =(3-а-b) +(5-а-2b) =(9+a +d 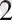-6a-6b+2ab) +(25+a 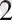+4b 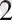-10a-20b+4ab) =2a 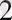+5b 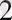+6ab-16a-26b+34 (2) . Енді S min болатындай а мен b ның мәндерін таңдау керек. Ол үшін дифференциалдық есептеуді қолданып, а мен b ның мәндерін табамыз:

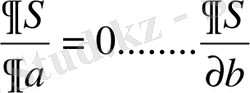=0 (3)

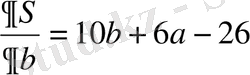(4)

Бұдан 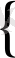2а+3 b -8=0 теңдеулер жүйесін шешеміз

3а+5 b-13=0

Сонда регрессия теңдеуі мына түрде болады: У=1+2х

Дұрыс қортындыға келгенді тексеру үшін қалдықты есептейміз:

l =3-а- b=3-1-2=0

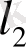=5-а-2 b=5-1-4=0 (5)

Қалдықтар нольге тең, бұл деген регрессия сызығы нақты екінүкте арқылы өтеді деген сөз.

Мысал 2. Енді алдыңғы мысалға 3-ші бақылауды қосайық: у=6, х=3 болғанда. Мұнда 3 нүкте 1 түзу бойында жатпайды, сондықтан нақты сәйкестік алу мүмкін емес. Мұндай жағдайда түзудің орнын анықтау үшін ең кіші квадтаттар әдісі бойынша регрессияны қарастырамыз.

Cызықтық функция

Yр = а+bt (2)

Мұнда a және b - теңдеупараметрлері; t - уақыт.

b параметрі регрессия коэффициенті, дамудың бағытын анықтайды. Кіші квадраттар әдісі бойынша a және b параметрлерін табамыз:

a=Y _ср -bt _ср

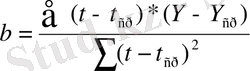Мұнда t _ср - уақыт факторының орташа мәні;

Y _ср - зерттелетін көрсеткіштердің орташа мәні.

Мысал - Тоғыз ай бойы жүргізілген акция туралы нақты деректерді алып, олардың сызықтық моделін құрайық. 1 Кестеде аралық есептеулер мен сызықтық модельді пайдалану нәтижелері келтірілген. Соңғы жолда колонка түрде мәндердің қосындысы берілген. Анықтайық: Y _{ср =} 504/9=56; t _{ср =} 45/9=5

Есептелген мәндерді жоғарғы формулаға қойсақ, мына мәндерді аламыз

b = 428/60=7, 13

a = 56-7, 13*5=20, 35

Кесте 1

Y(t)

t- t _ср

(t- t _ср ) ²

Y- Y _ср

(t- t _ср ) ( Y- Y _ср )

Yp(t)

E(t)

t: 1

Y(t): 25

t- tср: -4

(t- tср)2: 16

Y- Yср: -31

(t- tср) ( Y- Yср): 124

Yp(t): 27. 5

E(t): -2. 5

t: 2

Y(t): 34

t- tср: -3

(t- tср)2: 9

Y- Yср: -22

(t- tср) ( Y- Yср): 66

Yp(t): 34. 6

E(t): -0. 6

t: 3

Y(t): 42

t- tср: -2

(t- tср)2: 4

Y- Yср: -14

(t- tср) ( Y- Yср): 28

Yp(t): 41. 7

E(t): 0. 3

t: 4

Y(t): 51

t- tср: -1

(t- tср)2: 1

Y- Yср: -5

(t- tср) ( Y- Yср): 5

Yp(t): 48. 9

E(t): 2. 1

t: 5

Y(t): 55

t- tср: 0

(t- tср)2: 0

Y- Yср: -1

(t- tср) ( Y- Yср): 0

Yp(t): 56

E(t): -1

t: 6

Y(t): 67

t- tср: 1

(t- tср)2: 1

Y- Yср: 11

(t- tср) ( Y- Yср): 11

Yp(t): 63. 1

E(t): 3. 9

t: 7

Y(t): 73

t- tср: 2

(t- tср)2: 4

Y- Yср: 17

(t- tср) ( Y- Yср): 34

Yp(t): 70. 3

E(t): 2. 7

t: 8

Y(t): 76

t- tср: 3

(t- tср)2: 9

Y- Yср: 20

(t- tср) ( Y- Yср): 60

Yp(t): 77. 4

E(t): -1. 4

t: 9

Y(t): 81

t- tср: 4

(t- tср)2: 16

Y- Yср: 25

(t- tср) ( Y- Yср): 100

Yp(t): 84. 5

E(t): -3. 5

t: 45

Y(t): 504

t- tср: 0

(t- tср)2: 60

Y- Yср: 0

(t- tср) ( Y- Yср): 428

Yp(t): 504

E(t): 0

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

Ұқсас жұмыстар

Сызықтық емес регрессия және корреляция

Сызықтық емес регрессиялардың түрлері

Банктік ісінің дамуын болжамдаудың түрлері мен модельдері

Мектеп математика курсындағы математикалық статистика элементтері

Экономика дәрістер кешені

Регрессиялық талдау

12-Лекция. Модельдердің өзгешеліктерін анықтау мәселелері

Эконометрика - экономика мамандықтарына арналған оқу - әдістемелік құрал

Компьютерде корреляциялық талдау мәселелері

Есептеу математикасына кіріспе пәні бойынша оқу-әдістемелік кешен

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz