Гармониялық осциллятор

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Шәкәрім атындағы Семей мемлекеттік университеті.

СӨЖ

Тақырыбы: Гармониялық осциллятор.

Орындаған: Шаяхметова. Т. С

Тобы: Т-323

Тексерген: Мешетова Ж. С

Семей 2015

Гармониялық осциллятор.

Дененің күш əсерімен тербелуі үрдісін сандық жағынан сипаттау үшін Ньютон механикасы заңдарын пайдалану қажет. Серіппенің серпімділік күші əсерінен тербелуші дененің (мысалы домалақ шар) қозғалысын қарастырайық ( $F\ = \ - \ kx$ ) .

Үйкеліс күшінің қозғалысқа тигізетін əсерін есепке алмаймыз.

Шарик үшін Ньютонның екінші заңының теңдеуі мына түрде болады:

$m\ddot{x} = - kx$ , (7. 15)

мұнда x - тепе-теңдік қалпына дейінгі қашықтық, $\ddot{x}$ - уақыт бойындағы координатаның екінші туындысы, ал k - серіппенің қатаңдығы.

(7. 15) түріндегі теңдеу гармониялық тербелістер теңдеуі деп аталады, ал

осы кіші тербелістерді іске асырушы жүйе сызықтық немесе гармониялық

осциллятор деп аталады. Осылайша, серіппеде тербелуші дене сызықтық

осциллятор моделі боп табылады.

Сызықтық осциллятордың басқадай мысалы ретінде ауытқу бұрышы

жеткілікті түрде аз болатын физикалық жəне математикалық маятниктерді

қарауға болады.

$w_{0}^{2} = \frac{k}{m}$ белгісін енгізе отырып (7. 15) теңдеуін былай түрлендірейік:

$\ddot{x} + w_{0}^{2}x = 0$ (7. 16)

Сонымен, үйкеліс күші жоқ кезде серпімді күш əсеріндегі қозғалыс (7. 16)

дифференциалды теңдеумен сипатталады. Бұл теңдеу гармониялық

тербелістер теңдеуі деп аталады.

(7. 16) теңдеуінің жалпы шешімі мынадай:

$x = acos(w_{0}t + \varphi)$ (7. 17)

мұнда a мен ϕ - еркін тұрақтылар.

Сонымен, x-ң орнынан жылжуы уақыт өте косинус заңы бойынша

өзгереді. Демек, $F = - kx$ түріндегі күштің əсерінде тұрған жүйенің қозғалысы

гармониялық тербеліс түрінде болады.

Гармониялық тербеліс графигі, яғни (7. 17) функциясының графигі, оған

кіруші параметрлермен бірге 8. 2 суретте көрсетілген.

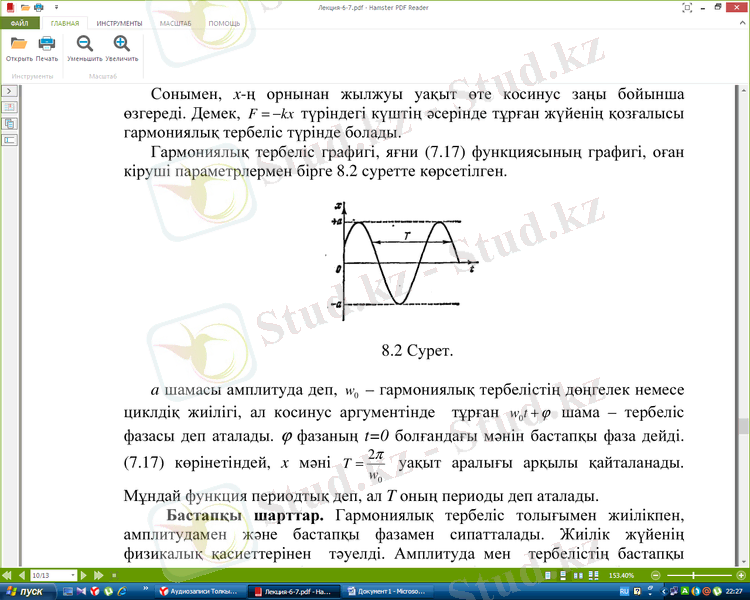
a шамасы амплитуда деп, $w_{0}$ - гармониялық тербелістің дөңгелек немесе

циклдіқ жиілігі, ал косинус аргументінде тұрған $w_{0}t + \varphi$ шама - тербеліс

фазасы деп аталады. $\varphi$ фазаның t=0 болғандағы мəнін бастапқы фаза дейді.

(7. 17) көрінетіндей, x мəні $T = \frac{2\pi}{w_{0}}\$ уақыт аралығы арқылы қайталанады.

Мұндай функция периодтық деп, ал T оның периоды деп аталады.

Бастапқы шарттар. Гармониялық тербеліс толығымен жиілікпен,

амплитудамен жəне бастапқы фазамен сипатталады. Жиілік жүйенің

физикалық қасиеттерінен тəуелді. Амплитуда мен тербелістің бастапқы

фазасын анықтау үшін материялық нүктенің қандай - да бір уақыт

мезетіндегі орны мен жылдамдығын білу керек. Егер тербеліс теңдеуі (7. 17)

түрінде өрнектелген болса, ал t=0 мезетінде координата мен жылдамдық

соған сəйкес $x_{0}$ және $v_{0}\$ -дерге тең болса, онда (7. 17) -нің негізінде мынаны

жаза аламыз:

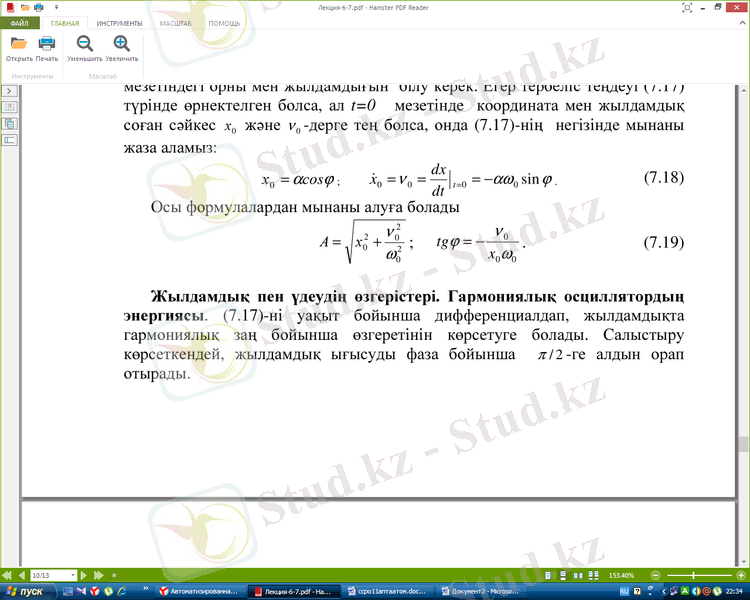Осы формулалардан мынаны алуға болады

Жылдамдық пен үдеудің өзгерістері. Гармониялық осциллятордың

энергиясы. (7. 17) -ні уақыт бойынша дифференциалдап, жылдамдықта

гармониялық заң бойынша өзгеретінін көрсетуге болады. Салыстыру

көрсеткендей, жылдамдық ығысуды фаза бойынша $\frac{\pi}{2}$ -ге алдын орап

отырады.

(7. 17) - ні уақыт бойынша екі рет дифференциалдап үдеу үшін өрнекті

табуға болады. Анализ көрсететіндей, үдеу мен ығысу қарама-қарсы фазада

болады.

Квазисерпімді күш консервативті болып табылады. Сондықтан

гармониялық тербелістің толық энергиясы тұрақты болып қалуы керек.

Толық энергия үшін формула:

Тербелістердің қосылуы. Соғулар. Бір бағыттағы екі қосылушы

гармониялық тербелісті жиілігі бойынша бір бірінен аса айырмашылығы

бола қоймайтын жағдайда қарастырайық. Осы үрдіс практикада ерекше

қызығушылық тудырады. Мұндай жағдайда қорытқы қозғалысты

амплитудасы пульсацияланатын гармониялық тербеліс ретінде қарастыруға

болады. Мұндай тербелістер соғулар деп аталады.

Өшетін тербелістер. Сызықтық осциллятордың еркін тербелістері

сыртқы күштер жоқ кезде өтеді. Сыртқы күш боп саналатын үйкеліс кезінде

сызықтық осциллятордың тербеліс энергиясы азаяды, ал ендеше, тербеліс

амплитудасы да төмендейді. Үйкеліс бар кездегі тербелістер өшетін бола

бастайды. Үйкеліс күші жылдамдыққа қарсы əрекет етеді. Демек, сызықтық

осциллятор үшін оның əсері қайта оралтушы күштің азаюына, яғни,

серіппенің серпімділігіне (k шамасының азаюы) эквивалентті. Егер 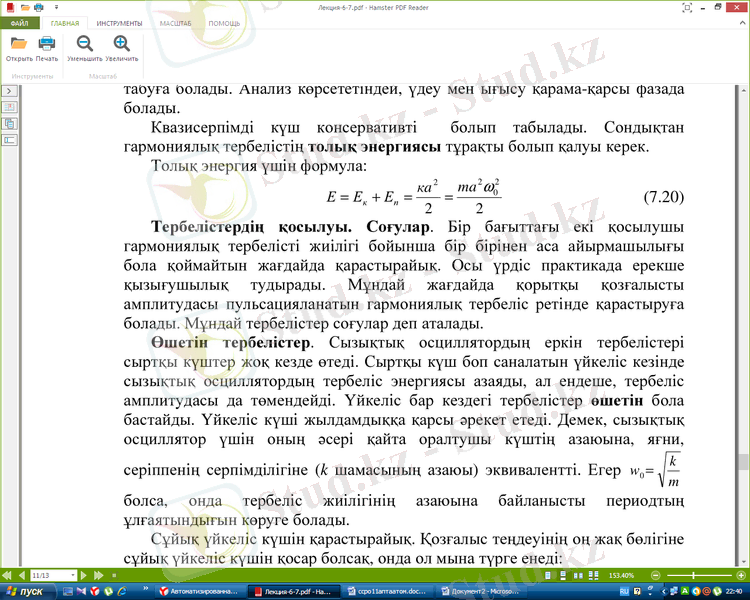болса, онда тербеліс жиілігінің азаюына байланысты периодтың

ұлғаятындығын көруге болады.

Сұйық үйкеліс күшін қарастырайық. Қозғалыс теңдеуінің оң жақ бөлігіне

сұйық үйкеліс күшін қосар болсақ, онда ол мына түрге енеді:

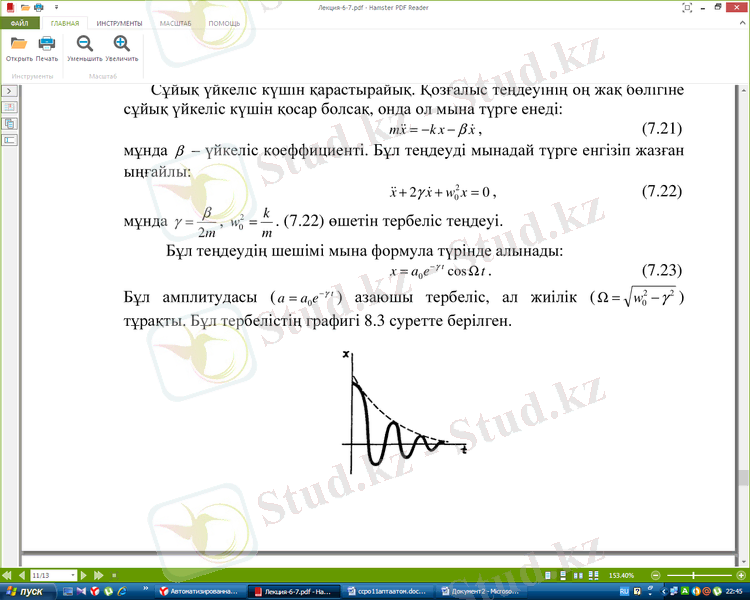
мұнда β - үйкеліс коеффициенті. Бұл теңдеуді мынадай түрге енгізіп жазған

ыңғайлы:

мұнда

өшетін тербеліс теңдеуі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

Ұқсас жұмыстар

Гармониялық тербелістің энергиясы

Қарапайым гармоникалық осциллятор

Тербелмелі қозғалыстар

Кристалдарды классификациялау

Гармониялық тербелістер

Бір еркіндік дәрежесі бар механикалық жүйенің тербеліс теңдеулеріне талдау жасау, тербелістің сөну дәрежесінің жүйенің қатаңдығы мен демпферлік қасиеттеріне тәуелділігі

Физикалық маятник

Өшетін тербелістер

Pascal программалау тілінде математикалық маятник тербелісін моделдеу

Кванттық механикадағы қозғалыстың ерекшеліктері

Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

Ақпарат

Қосымша

Email: info@stud.kz