Икемділік коэффициенті туралы

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Қазақстан Республикасының Білім және Ғылым министрлігі

Семей қаласының Шәкәрім атындағы мемлекеттік университеті

ОӨЖ

Тақырыбы : Икемділік коэффициенті

Орындаған: Кабенова А. С

Топ: УА-303

Тексерген :Жақсыгулова Д. Д

Икемділік коэффициенті

Егер экономикалық Егер экономикалық Егер экономикалық

Семей 2015 жыл

Икемділік коэффициенті

Икемділік коэффициенті былай анықталады:

% Q _d

Е _d =

% Р

Мұндағы: Е _d- сұраныс икемділігінің коэффициенті;

% Q _d - сұраныс көлемінің өсу пайызы (%) ;

% Р- бағаның төмендеу пайызы (%) .

1. 3. - сызба. Сұраныстың икемділігі.

Мұндағы: «А»- біркелкі икемділік, «В»- икемді, «С» - икемсіз сұранысты бейнелейді.

Қазіргі экономикалық ғылымда табысқа қатысты сұраныс икемділігі көрсеткіші де пайдаланылады.

Ұсыныс - тауар өндірушілердің нарыққа сатуға ұйғарған, бағасы белгіленген тауар жиынтығы. Ұсыныс өндірілген тауар ассортименті мен олардың бағасы арқылы қалыптастырады; ал сұраныс болса, тауар ұсынысының көлемімен құрылымын анықтайды, себебі тұтынушы мойындаған нәрсе ғана ұдайы өңдіріледі. Ұсыныс бағаға тура қатынаста болады: баға жоғары болса, онда сатушылар тарапынан тауарды ұсыну көбірек болады. Баға мен ұсыныстың осындай қатыста болуы ұсыныс заңы деп аталады.

Жалпы түрі: Q _S = f(Р) .

Ондағы: Q _S - ұсыныс шамасы (supply) ; Р - баға.

Баға мен ұсынылған өнім саны арасындағы тікелей байланыс ұсыныс заңы деп аталады. Өндірілген игіліктер санының баға деңгейіне тәуелді болуын графикалық түрде көрсетуге болады (1. 5-сызбаны қараңыз) .

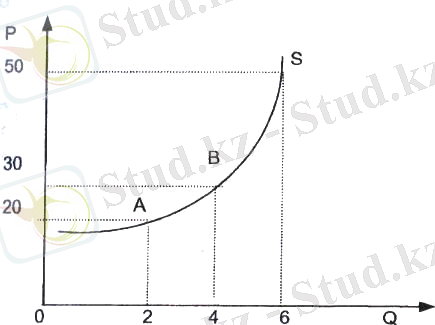
1. 1-сызба. Ұсыныс шамасының бағаға тәуелді

Ұсыныс қисығы (suppiy curve) - өндірушілердің дәл осы уақытта түрлі бағамен сатқысы келетін экономикалық игілік санын көрсететін қисық.

Ұсынысқа бағадан басқа әсер етуші факторлар:

1) өндіріс ресурс факторларының бағасы;

2) технология;

3) рыноктық экономика агенттерінің бағаны және тапшылықты күтуі;

4) салықтар мен субсидиялар көлемі;

5) сатушылар көлемі.

Ұсыныс көлемінің өзгеру дәрежесінің нарықтық бағаның ұлғаюын сипаттауы, ұсыныс икемділігі болып табылады.

Икемділік коэффициенті былай анықталады:

% * Q

Е _s =

%* Р

Мұндағы: Е _s- ұсыныс икемділігінің коэффициенті;

% Q - ұсыныс көлемінің өсу пайызы (%) ;

% Р- баға ұлғаюының пайызы (%) .

Ұсыныс икемділігінің коэффициенті мынаны көрсетеді: егер нарықтық баға көтерілсе немесе белгілі пайызға түссе, ұсынатын тауар санының қалай өзгергендігін байқатады.

Ұсыныс мөлшері мынадай формуламен анықталады:

Qs= F (Б* Тс* C _d * K _ж ),

мұндағы: Qs - бар тауардың ұсыным көлемі;

F - ұсынысты қалыптастыратын факторларға қатысты ұсыныс тәуелдігінің қызметі;

Б -қолдағы және жолдағы тауарлар бағасы;

Тс - қолданылатын өндіріс технологиясының сипаты;

C _d - салықтар мен дотациялар;

K _ж - табиғи- климаттық жағдай.

Өндірушілер өндірілген өнімнің көбін жоғарғы бағамен сатуды ұсынады. Қалыпты жағдайда баға жоғары болса, онда сатушылар тарапынан тауарды ұсыну көбірек болады. Керісінше тауар ұсынысы ұлғайған сайын, оларға баға төмендей түседі.

Егер экономикалық құбылыстар арасында сызықты емес қатыстар болса, онда оларды сызықты емес функциялар көмегімен өрнектеуге болады. Екі сызықты емес регрессия теңдеуінің класы бар;

Параметрлерді бағалау ЕККӘ бойынша табылады :

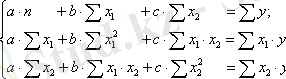
$C:\Users\Zhanar\Desktop\3_clip_image019.gif$

Кері алмастыру арқылы мынаны табамыз:

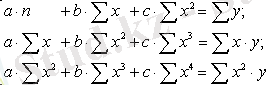
$C:\Users\Zhanar\Desktop\3_clip_image021.gif$

Тура байланыс кері байланысқа, немесе кері байланыстура байланысқа өзгереді. . Гиперболалық түрін сызықты түрге келтіру үшін мынадай алмастыру жасаймыз. приводится к линейному уравнению простой заменой 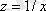$C:\Users\Zhanar\Desktop\3_clip_image023.gif$ . ЕККӘ қолданып, мынадай жүйе аламыз :

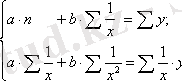
$C:\Users\Zhanar\Desktop\3_clip_image025.gif$

Осы тәртіппен 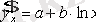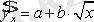$C:\Users\Zhanar\Desktop\3_clip_image026.gif$ , $C:\Users\Zhanar\Desktop\3_clip_image028.gif$ теңдеуінің түрлері де сызықты түрге келтіріледі. ие. Сызықты емес моделдерде дәрежелік функция жиі қолданылады, яғни 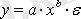$C:\Users\Zhanar\Desktop\3_clip_image030.gif$ , ол сызықты түру келтірілу үшін логарифмделеді:

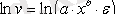
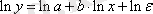
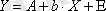
$C:\Users\Zhanar\Desktop\3_clip_image032.gif$ $C:\Users\Zhanar\Desktop\3_clip_image034.gif$ $C:\Users\Zhanar\Desktop\3_clip_image036.gif$

Мұндағы 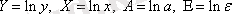$C:\Users\Zhanar\Desktop\3_clip_image038.gif$ . Яғни, ЕККӘ қолданылады және мынадай жүйе шығады:

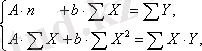
$C:\Users\Zhanar\Desktop\3_clip_image040.gif$

Содан кейін потенцирлейміз де ізделінді теңдеуді табамыз.
Дәрежелік функцияны кеңінен қолданатын себебіміз, b параметрі нақты экономикалық мәні болып табылады, яғни ол икемділік коэффициенті . Икемділік коэффициенті- егер фактор 1% ке өзгерсе онда нәтиже шамамен қаншаға өзгеретіндігін көрсететін коэффициент.

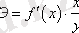$C:\Users\Zhanar\Desktop\3_clip_image044.gif$ .

Қалған функциялар үшін, икемділік коэффициенті тұрақты шамабола алмайды. Ол тек х фактрының мәндеріне байланысты болады. Сонда,

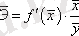$C:\Users\Zhanar\Desktop\3_clip_image046.gif$ .

Сызықты емес теңдеуде сызықты теңдеудегі сияқты байланыс тығыздығын есептеуге болады. Бұл жағадйжа корреляция индексі есептеледі:

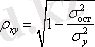
$C:\Users\Zhanar\Desktop\3_clip_image099.gif$

мұндағы 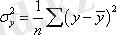$C:\Users\Zhanar\Desktop\3_clip_image101.gif$ - у шешуші белгінің жалпы дисперсиясы., 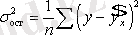$C:\Users\Zhanar\Desktop\3_clip_image104.gif$ - қалдық дисперсия 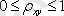$C:\Users\Zhanar\Desktop\3_clip_image106.gif$ . Егер нәтиже 1- ге жуықтаса, онда байланыс жақсы, теңдеу дұрыс құрылған деп есептеледі.
Детерминация коэффициентінің индексін есептейді:

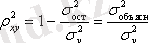
$C:\Users\Zhanar\Desktop\3_clip_image108.gif$

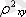$C:\Users\Zhanar\Desktop\3_clip_image110.gif$ детерминация индексін детерминация коэффициентімен салыстырамыз: регрессия сызығының қисығы үлкен болса, онда соғұрлым 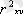$C:\Users\Zhanar\Desktop\3_clip_image112.gif$ шамасы 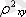$C:\Users\Zhanar\Desktop\3_clip_image110.gif$ нан кіші . Бұл алынған функцияның күрделілігін білдіреді. Сондықтан сызықты регрессия теңдеуін алу қажет.
Детерминация индексі регрессия теңдеуін Фишер критерийі бойынша тексеру үшін қолданылады.

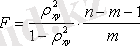
$C:\Users\Zhanar\Desktop\3_clip_image115.gif$

Мұндағы 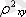$C:\Users\Zhanar\Desktop\3_clip_image110.gif$ - детерминации индексі, n - бақылау саны, m - х айнымалысы бойынша параметр саны, F - критерийінің нақты мәні кестелік мәнімен салыстырылады, егер α және еркін түсу көрсеткіші саны 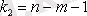$C:\Users\Zhanar\Desktop\3_clip_image125.gif$ қалдық квадраттар қосындысы үшін) және 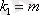$C:\Users\Zhanar\Desktop\3_clip_image127.gif$ (факторлық квадратының қосындысы үшін ) .

Егер фактордың айнымалыға тәуелділігін сызықтық теңдеу түрінде сипаттау мүмкін болмаса, онда сызықтық емес функция көмегімен сипаттауға болады. Сызықтық емес регрессияның парметрлерін қосылған параметрлері бойынша бағалау, сызықтық регрессия сияқты ең кіші квадраттар әдісі (ЕКӘ) арқылы анықталады, яғни бұл функциялар параметрлер бойынша сызықты. Кез келген полиномды көптік регрессияның сызықтық моделіне келтіруге болады. Соның ішінде икемділік коффициентін қолдану арқылы берілген мысалды қарастырайық.

Мақсаты: Икемділік коэффициентін қолдана отырып, Көптік регрессия теңдеуін құру, оның парметрлерін бағалау.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.