Нүктедегі кернеулік жағдайы және домалау үштіректеріндегі түйісу күшін есептеу


Қазақстан Республикасының Білім және Ғылым министрлігі
Семей қаласының Шәкәрім атындағы мемлекеттік Университеті
МӨЖ №11
Пән : «Есептеудің инженерлік тәсілдері»
Дайындаған: Магистрант Қуанышұлы Д.
6М071200 «Машина жасау»
Тексерген: т. ғ. д. профессор, Темиртасов О. Т.
Семей 2015 жыл.
ЖОСПАР:
- НҮКТЕДЕГІ КЕРЕНУЛІК ЖАҒДАЙ. ТЕПЕ-ТЕҢДІК ТЕҢДІГІ.
- ДОМАЛАУ ҮШТІРЕКТЕРІНДЕГІ ТҮЙІСУ КҮШІН АНЫҚТАУ
- ЖАНАСАТЫН ДЕНЕЛЕРДІҢ ГЕОМЕТРИЯСЫ. ДОМАЛАУ ҮШТІРЕКТЕРІНДЕГІ ТҮЙІСУ КҮШІНІҢ ШАМАСЫН АНЫҚТАУ.
- НҮКТЕДЕГІ КЕРЕНУЛІК ЖАҒДАЙ. ТЕПЕ-ТЕҢДІК ТЕҢДІГІ.
Жүктелудің жалпы жағдайындағы тепе-теңдік жағдайында орныққан дененің кез-келеген нүктесіндегі кернеулік жағдайын сипаттау үшін оның шеттерін жиектері координаталық өске параллель параллелепипед түріндегі көлем бөліп алайық (сурет 3. 1) .
Егер параллелепипед өлшемдерін кемітсе ол осы нүктені қысатын болады. (dx, dy, dz) аралығында параллелепипед барлық жиектері қарастырылып отырған нүкте арқылы өтеді және параллелепипед сәйкес жазықтықтарындағы кернеу қарастырылып отырған нүктедегідей болады.
Параллелепипед алаңындағы толық кернеу үш құраушыға бөлінуі мүмкін, біреуі жазықтыққа нормаль, ал екеуі жазықтық бойынша.
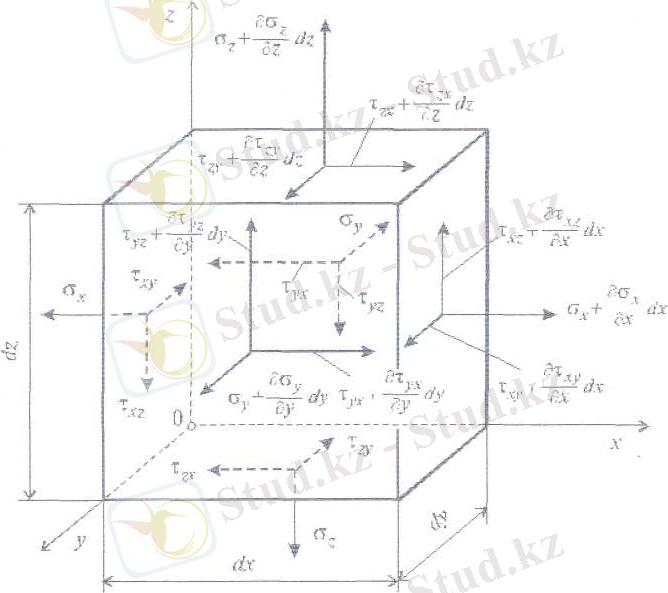
Сурет 3. 1.
Қалыпты және жанама кернеулер σ мен τ арқылы, сйкесінше индекстерімен σ xx , σ yy . . . , τ zx белгіленеді. Бірінші индекс берілген кернеу әсер ететін алаңға перпендикуляр координаталық өскең, ал екінші индекс өзі бағытталған алаң бойына келетін өсті көрсетеді.
Қалыпты кернеулер индекстері бірдей болғандықтан олар үшін бір өлшемді индексацияны да қолднаады: σ xx = σ x , σ yy = σ y , σ zz = σ z . Өстер бағытталуы ерікті.
Белгі ережесін келесідей болып қабылдаймыз: егер алаңнын сырқы нормалі сәйкес өстің оң бағытына сәйкес келсе, ол әсер етеін өс оң бағыты бойымен бағытталса онда кернеу оң болып саналады.
параллелепипед тепе-теңдік жағдайының үш шартынан координаталық өстер түріндегі моменттер қосындысы түріндегі келесідей маңызды тұжырымдарды алуға болады:
 (3. 1)
(3. 1)
Жалпы қабырғаға ортақ жанама кернеулерді құрайтын екі өзара перпендикуляр алаңдарда екеуі де шамасы мен бағыты бойынша не қабырғаға, не оған қарсы бағытталады. Бұл тұжырым-жалпы түрдегі жанама кернеулердің жұптылық заңы болып табылады.
Параллелепипедті координаталық өстер бағыты бойынша үштер қосындысы ретінде қарастырып және екінші ретті кішігірім шамаларды есепке алмай тепе-теңдік жағдайының келесідей теңдігін алуға болады:
 (3. 2)
(3. 2)
Жанама кернеулердің жұптылық заңы (3. 1), (3. 2) теңдігі алты белгіссіз кернеуі бар: σ x , σ y , σ z , τ xу , τ xz , τ yz .
Статиканың тепе-теңдік жағдайының теңдіктерінің саны (3. 2) белгіссіз кернеулерден аз болғандықтан жүктелудің жалпы жағдайындағы тепе-теңдік жағдайында орныққан дененің кез-келеген нүктесіндегі кернеулік жағдайын анықтау статикалық анықталмайды.
- ДОМАЛАУ ҮШТІРЕКТЕРІНДЕГІ ТҮЙІСУ КҮШІН АНЫҚТАУ.
Сурет 15. 3 көрсетілген шарикті үштіректі қарастырайық. .
Ішкі сақина жағынан түсетін N жүктеуді қабылдау 180° доғада орналасқан шариктер қатысады. Мейлінше үлкен жүктеуді F o N күшінің өсінде орналасқан шарик қабылдайды. Өске қатысты симетриялы орналасқан шарикге бірдей қысым түседі.
Ішкі сақинаның тепе - теңдік шартынан келесі туындайды
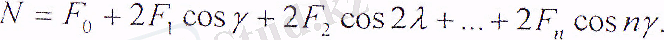 (15. 7)
(15. 7)
Үштірктегі саңылаудың жоқтығы және сақиналар иілуін ескермей, шариктер мен сақиналар үшін келесі тәуелділіктерді қабылдауға болады:
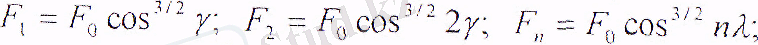 (15. 8)
(15. 8)
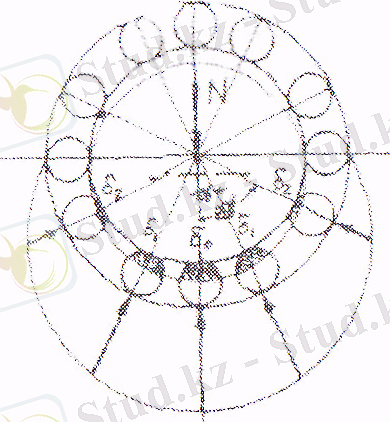
сур. 15. 3
мұнда n-жүктеу аймағындағы домалау денелерінің жартысы
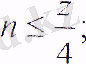
z - домалау денелерінің жалпы саны (шариктер) .
Бұл тәуелділіктерді тепе - теңдік шарттарына қойып келесіні аламыз:
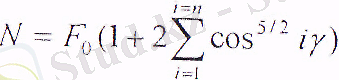 (15. 9)
(15. 9)
Осыдан
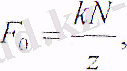 (15. 10)
(15. 10)
мұнда
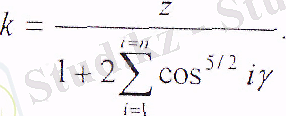 (15. 11)
(15. 11)
Шариктер саны Z=10÷20 үштіректер үшін k= 4, 37±0, 01
Саңылаумен жұмыс істейтін үштіректер үшін k= 5 деп қабылдайды. Екі қатарлы үштірктерде күштердің бір келкі тараламауы салдарынан к=6 .
Осыған ұқсас роликті үштіректердегі қысым анықталады.
- ЖАНАСАТЫН ДЕНЕЛЕРДІҢ ГЕОМЕТРИЯСЫ. ДОМАЛАУ ҮШТІРЕКТЕРІНДЕГІ ТҮЙІСУ КҮШІНІҢ ШАМАСЫН АНЫҚТАУ.
Жанасатын денелердің геометриясы.
Екі дене қандай да бір нүктеде жанасады, бұл нүктені координата басы болып қабылдаймыз. х 1 , у 1 , z 1 жүйесін бірінші денеге, ал х 2 , у 2 , z 2 жүйесін екінші денеге жатқызамыз (сур. 12. 1) . z 1 и z 2 өстері жанасатын дене беттерінің жалпы нормаліне сәйкес келеді. Жанасу нүктесінің айналасындағы қисық сызықты беттің теңдеуі келесідей болсын дейік


Сур. 15. 1
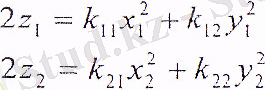 (15. 1)
(15. 1)
жалпы жағдайда x l , y 1 и x 2 , y 2 өстері сәйкес келмейді.
Бір нүктеде түйісетін екі дененің икемді деформациясын қарастырйық (сурет 15. 2) . Дене материалы - изотропты.
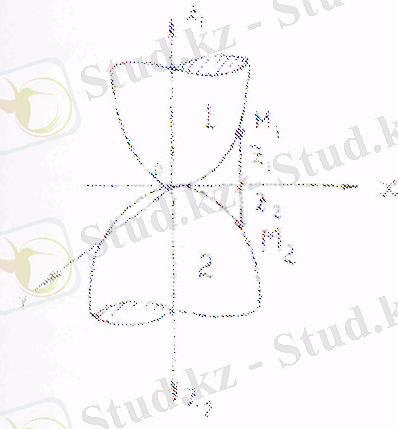
сур. 15. 2
Дене қысылуы z 1 z 2 өсі бойымен бағытталған күштер тарапынан болады. деформация нәтижесінде 1 және 2 денелердің нүктелік жанасуы О нүктесі айналасында белгілі алаң бойынша өтеді.
xyz 1 координата жүйесі дене 1 шексіздікте, ал связана на xyz 2 координата жүйесі дене 2 шексіздікте байланысқан дейік. Өрнек деформация кезіндегі дене 1 және 2 жақындауын көрсетеді
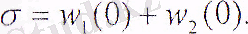 (15. 2)
(15. 2)
Эллипсті алаң орталығындағы максималды қысым өрнегін қолдану арқылы келесі өрнекті алуға болады:
а) жанасу аланының элипсті жартылай өсі
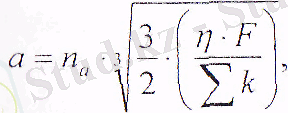 (15. 3)
(15. 3)
б) кіші жартылай өс
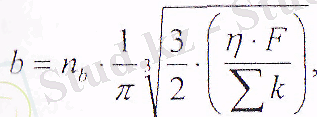 (15. 4)
(15. 4)
в) жанасу аланының орталығындағы максималды қысым
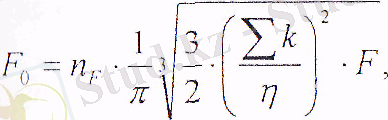 (15. 5)
(15. 5)
г) жанасатын денелердің жақындауы
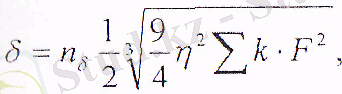 (15. 6)
(15. 6)
4. ӘДЕБИЕТТЕР:
1. «Расчет на прочность в машиностроении» С. Д. Понамарев и др. Том І -ІІІ, -М: Машгиз, 1956-1959.
2. Прочность и устоичивость колебания. Справочник Том І-ІІІ-М: Машиностроение, 1968.
3. Тимошенко С. П. Теория упругости. -М:НСУКА, 1975-576с.
4. Работнов Н. Н. Механика твердого деформируемого тела. -М: 1979-744с.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz