Жай және дербес туындылы дифференциалдық теңдеулерді шешу


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
СЕМЕЙ ҚАЛАСЫНЫҢ ШӘКӘРІМ АТЫНДАҒЫ МУ
СӨЖ
Тақырыбы: Жеке туындылардағы дифференциал теңдеулерді шешу
Тексерген: Нургалиев Д. Н.
Семей 2015 ж.
МАЗМҰНЫ
КІРІСПЕ3
1 ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР4
2. Дербес туындылы дифференциалдық теңдеу. 7
3 Сызықтық және сызықтық емес дифференциалдық теңдеулер11
ҚОРЫТЫНДЫ12
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР13
Дифференциалдық теңдеулер - функциясы бар туынды функциясының мәнін қатысты теңдеу, тәуелсіз айнымалы сандар мәндер (параметрлері) . Теңдеудің туынды тәртібі (формальды ол шектелген жоқ) әр түрлі болуы мүмкін. Туынды қаржы құралдары функциялары тәуелсіз айнымалылар және параметрлер әр түрлі комбинациялары немесе барлық теңдеулер енгізілген, бірақ кем дегенде бір туынды өзі жоқ болуы мүмкін. Белгісіз функцияның бар туынды емес, кез-келген теңдеу дифференциалдық теңдеу болып табылады. Мысалы, \ F (х) = F (F (X) ) дифференциалдық теңдеу болып табылады.
Жоғары ретті дифференциалдық теңдеу теңдеулер саны бастапқы теңдеудің мақсатында тең, онда бірінші ретті теңдеулер жүйесі айналдыруға болады. Тиімді аналитикалық нысанда, оның шешімі түбіртек талап етпей қарапайым дифференциалдық теңдеулер сандық шешімін қамтамасыз ету үшін қазіргі заманғы жоғары жылдамдықты компьютерлер.
Дифференциалдық теңдеулер 17 ғасырдың соңында механика, т. б. жаратылыстану пәндерінің талабына сәйкес интегралдық есептеу және дифференциалдық есептеумен қатар пайда болды. Қарапайым дифференциалдық теңдеулер Ньютонның және неміс математигі Лейбництің) еңбектерінде кездеседі. “Дифференциалдық теңдеулер” терминін ғылымға Лейбниц енгізген (1676) . Тәуелсіз бір айнымалыға тәуелді бір немесе бірнеше функциялардың туындылары бар дифференциалдық теңдеулерді жай дифференциалдық теңдеу деп, ал тәуелсіз бірнеше айнымалыға тәуелді функциялардың дербес туындылары бар дифференциалдық теңдеулерді дербес туындылы дифференциалдық теңдеу деп атайды. Дифференциалдық теңдеулерге енетін туындылардың реті дифференциалдық теңдеулердің реті делінеді.
1 ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДифференциалдық теңдеулер ізделініп отырған функция қамтитын тәуелсіз айнымалылардың санына байланысты жай және дербес туындылы дифференциалдық теңдеулер болып екі класқа бөлінеді.
1. 1. Жай дифференциалдық теңдеулер. Жай дифференциалдық теңдеулер теориясы төменгі курста қарастырылғандықтан, бұл пунктте ілгеріде керек болатын негізгі ұғымдар мен теоремаларды қарастырамыз.
1. 1. 1-анықтама.
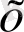 -тәуелсіз айнымалысын, оған байланысты анықталатын ізделінді
-тәуелсіз айнымалысын, оған байланысты анықталатын ізделінді
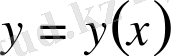 функциясын және оның
функциясын және оның
 туындыларын байланыстыратын теңдеуді
жай дифференциалдық теңдеу
деп атайды.
туындыларын байланыстыратын теңдеуді
жай дифференциалдық теңдеу
деп атайды.
Қысқаша жай дифференциалдық теңдеуді
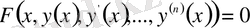 (1. 1. 1)
(1. 1. 1)
теңдігі түрінде жазады.
Егер (1. 1. 1) теңдеуі ізделінді
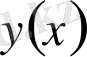 функциясының жоғарғы ретті туындысына байланысты шешілетін болса, онда оны
функциясының жоғарғы ретті туындысына байланысты шешілетін болса, онда оны
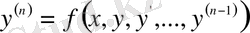 (1. 1. 2)
(1. 1. 2)
теңдігі түрінде жазуға болады.
Жай дифференциалдық теңдеу (1. 1. 1) түрінде берілсе оны
айқындалмаған
, ал (1. 1. 2) түрінде берілсе
айқындалған түрде
берілген теңдеу деп атайды. (1. 1. 1) - теңдеуіне қатысатын ізделінді
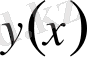 функциясының туындыларының ең жоғарғы реті жай дифференциалдық теңдеудің
реті
деп аталады.
функциясының туындыларының ең жоғарғы реті жай дифференциалдық теңдеудің
реті
деп аталады.
1. 1. 2 - анықтама.
1)

2)
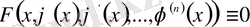
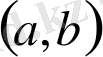 интервалында анықталған жоғарыда көрсетілген 1) - 2) шарттарды қанағаттандыратын
интервалында анықталған жоғарыда көрсетілген 1) - 2) шарттарды қанағаттандыратын
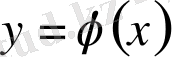 функциясын жай дифференциалдық теңдеудің
классикалық
шешімі
деп атайды.
функциясын жай дифференциалдық теңдеудің
классикалық
шешімі
деп атайды.
(1. 1. 2) теңдеуінің
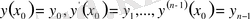 қосымша шарттарды қанағаттандыратын шешімін іздестіруді
Коши есебі
деп атайды. Мұндағы
қосымша шарттарды қанағаттандыратын шешімін іздестіруді
Коши есебі
деп атайды. Мұндағы
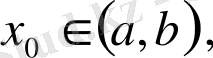
 - берілген белгілі сандар. Жеке жағдайда, бірінші ретті жай дифференциалдық теңдеуге қойылатын Коши есебі
- берілген белгілі сандар. Жеке жағдайда, бірінші ретті жай дифференциалдық теңдеуге қойылатын Коши есебі
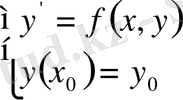 (1. 1. 3)
(1. 1. 3)
Ал екінші ретті жай дифференциалдық теңдеуге қойылатын Коши есебі
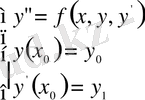 (1. 1. 4)
(1. 1. 4)
жүйелері арқылы анықталады.
Коши есебінің қай уақытта шешімі бар және жалғыз болатындығы туралы сұраққа Пикар теоремасының тұжырымы жауап береді. Екі дербес жағдай үшін осы теореманың тұжырымын келтірейік.
1-жағдай.
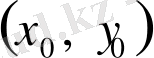 нүктесін қамтитын
нүктесін қамтитын
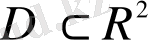 облысында
облысында
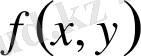 функциясы анықталған, үзіліссіз және осы облыста
функциясы анықталған, үзіліссіз және осы облыста
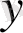 аргументі бойынша үзіліссіз дербес туындысы
аргументі бойынша үзіліссіз дербес туындысы
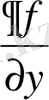 бар болсын. Онда бірінші ретті жай дифференциалдық теңдеуге қойылатын Коши есебінің
бар болсын. Онда бірінші ретті жай дифференциалдық теңдеуге қойылатын Коши есебінің
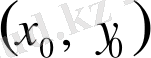 нүктесінің маңайында жалғыз шешімі бар болады.
нүктесінің маңайында жалғыз шешімі бар болады.
2-жағдай.
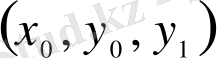 нүктесін қамтитын
нүктесін қамтитын
 облысында
облысында
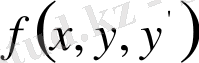 функциясы анықталған, үзіліссіз және оның осы облыста
функциясы анықталған, үзіліссіз және оның осы облыста
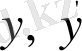 аргументтері бойынша үзіліссіз
аргументтері бойынша үзіліссіз
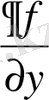 ,
,
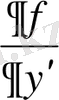 дербес туындылары бар болсын. Онда екінші ретті жай дифференциалдық теңдеуге қойылатын Коши есебінің
дербес туындылары бар болсын. Онда екінші ретті жай дифференциалдық теңдеуге қойылатын Коши есебінің
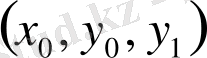 нүктесінің маңайында жалғыз шешімі бар болады.
нүктесінің маңайында жалғыз шешімі бар болады.
Сызықты теңдеу жай дифференциалдық теңдеулердің ішіндегі ең қарапайым жақсы зерттелген теңдеу. Ізделінді функция мен оның туындыларының тек бірінші дәрежесі қатысатын және теңдеудің коэффициенттері тек тәуелсіз айнымалыға байланысты анықталатын теңдеуді сызықты жай дифференциалдық теңдеу деп атайды. Сызықты жай дифференциалдық теңдеудің жалпы түрі
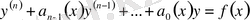 (1. 1. 4)
(1. 1. 4)
теңдігі түрінде анықталады. Мұндағы
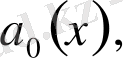
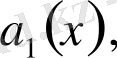
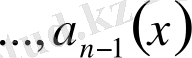 - теңдеудің
коэффициенттері
, ал
- теңдеудің
коэффициенттері
, ал
 -
бос мүшесі
деп аталады. Бұлар белгілі функциялар. Егер
-
бос мүшесі
деп аталады. Бұлар белгілі функциялар. Егер
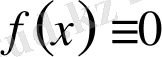 болса, онда мұндай теңдеу
біртекті
, ал
болса, онда мұндай теңдеу
біртекті
, ал
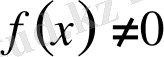 болса, онда
біртекті емес сызықты жай дифференциалдық теңдеу
деп аталады.
болса, онда
біртекті емес сызықты жай дифференциалдық теңдеу
деп аталады.
1. 1. 1 - теорема.
(
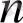 -ші ретті, біртекті сызықты жай дифференциалдық теңдеудің жалпы шешімінің құрылымы туралы) . Егер
-ші ретті, біртекті сызықты жай дифференциалдық теңдеудің жалпы шешімінің құрылымы туралы) . Егер
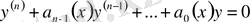
теңдеудің коэффициенттері
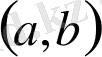 интервалында үзіліссіз болса, онда оның жалпы шешімі
интервалында үзіліссіз болса, онда оның жалпы шешімі
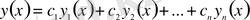
теңдігі түрінде анықталады. Мұндағы
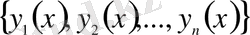 - теңдеудің сызықты тәуелсіз дербес шешімдерінің жүйесі, ал
- теңдеудің сызықты тәуелсіз дербес шешімдерінің жүйесі, ал
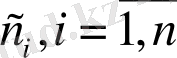 - кез-келген тұрақтылар.
- кез-келген тұрақтылар.
1. 1. 1 - ескерту.
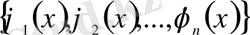 - функциялар жүйесі
- функциялар жүйесі
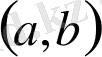 интервалында
сызықты тәуелсіз жүйе
деп аталады, егерде
интервалында
сызықты тәуелсіз жүйе
деп аталады, егерде
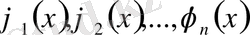 функцияларынан құралған
функцияларынан құралған
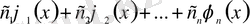
сызықтық комбинация
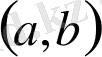 интервалында барлық
интервалында барлық
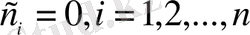 болғанда ғана нөлге тепе - тең болатын болса.
болғанда ғана нөлге тепе - тең болатын болса.
1. 1. 2 - теорема.
(
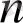 -ші ретті, біртекті емес сызықты жай дифференциалдық теңдеудің жалпы шешімінің құрылымы туралы) . Егер (1. 1. 4) теңдеудің коэффициенттері мен
-ші ретті, біртекті емес сызықты жай дифференциалдық теңдеудің жалпы шешімінің құрылымы туралы) . Егер (1. 1. 4) теңдеудің коэффициенттері мен
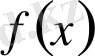 бос мүшесі
бос мүшесі
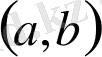 интервалында үзіліссіз болса, онда оның жалпы шешімі
интервалында үзіліссіз болса, онда оның жалпы шешімі
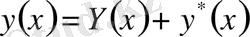
теңдігімен анықталады. Мұндағы
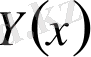 - біртекті, сызықты теңдеудің жалпы шешімі, ал
- біртекті, сызықты теңдеудің жалпы шешімі, ал
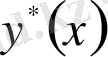 - біртекті емес, сызықты теңдеудің қандай да бір дербес шешімі.
- біртекті емес, сызықты теңдеудің қандай да бір дербес шешімі.
2 Дербес туындылы дифференциалдық теңдеу.
Мұнда және ілгеріде көп айнымалы
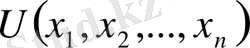 функциясын қарастырамыз. Мұнда
функциясын қарастырамыз. Мұнда
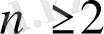 . Егер
. Егер
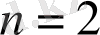 болса, онда тәуелсіз айнымалыларды
болса, онда тәуелсіз айнымалыларды
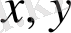 немесе
немесе
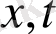 арқылы белгілейміз. Әдетте уақытты
арқылы белгілейміз. Әдетте уақытты
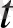 , ал түзудің бойындағы нүктенің координатасын
, ал түзудің бойындағы нүктенің координатасын
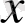 деп аламыз.
деп аламыз.
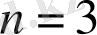 болған кезде тәуелсіз айнымалылар
болған кезде тәуелсіз айнымалылар
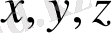 немесе
немесе
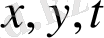 әріптерімен белгіленеді. Көп айнымалы функцияларының дербес туындыларын
әріптерімен белгіленеді. Көп айнымалы функцияларының дербес туындыларын
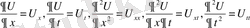
т. с. с. түрінде белгілеген өте ыңғайлы.
2. 1 - анықтама.
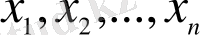 тәуелсіз айнымалыларын, ізделінді
тәуелсіз айнымалыларын, ізделінді
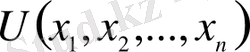 функциясын және оның
функциясын және оның
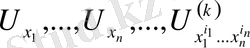
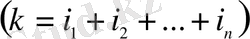 дербес туындыларын байланыстыратын теңдеуді
дербес туындылы дифференциалдық теңдеу
деп атайды. Қысқаша дербес туындылы дифференциалдық теңдеуді
дербес туындыларын байланыстыратын теңдеуді
дербес туындылы дифференциалдық теңдеу
деп атайды. Қысқаша дербес туындылы дифференциалдық теңдеуді
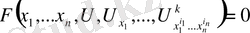 (1. 2. 1)
(1. 2. 1)
теңдігі түрінде жазады. Мұндағы
 (1. 2. 1) теңдеуіне қатысатын ізделінді
(1. 2. 1) теңдеуіне қатысатын ізделінді
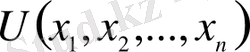 функциясының дербес туындыларының ішіндегі ең жоғарғы реті
теңдеудің реті
деп аталады. Мысалы,
функциясының дербес туындыларының ішіндегі ең жоғарғы реті
теңдеудің реті
деп аталады. Мысалы,
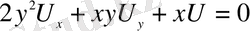
теңдігі бірінші ретті дербес туындылы дифференциалдық теңдеуді анықтайды.
2. 2 - анықтама.
1)
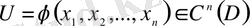
2)
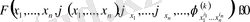
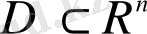 облысында анықталған жоғарыда көрсетілген 1) - 2) шарттарды қанағаттандыратын
облысында анықталған жоғарыда көрсетілген 1) - 2) шарттарды қанағаттандыратын
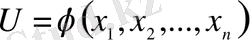 функциясын
дербес туындылы дифференциалдық теңдеудің классикалық шешімі
деп атайды.
функциясын
дербес туындылы дифференциалдық теңдеудің классикалық шешімі
деп атайды.
Осы кезде дербес туындылы дифференциалдық теңдеулер теориясы да өте қатты даму үстінде. Мұндай теңдеулерді жалпы жағдайда зерттеу өте қиын. Осы теңдеулердің ішінде сызықты теңдеулер толығырақ зерттелген. Біздің курста осындай теңдеулерді қарастыратын боламыз.
Ізделінді функция мен оның дербес туындыларының тек бірінші дәрежесі қатысатын және теңдеудің коэффициенттері тек тәуелсіз айнымалыларға байланысты анықталатын теңдеулерді сызықты дербес туындылы дифференциалдық теңдеулер деп атайды. Ізделінді функция екі тәуелсіз айнымалыға байланысты анықталатын, бірінші ретті сызықты дербес туындылы дифференциалдық теңдеудің жалпы түрі
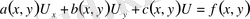 (1. 2. 2)
(1. 2. 2)
түріндегі теңдік арқылы анықталады. Мұндағы
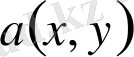 ,
,
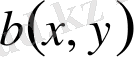 ,
,
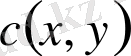 -теңдеудің коэффициенттері, ал
-теңдеудің коэффициенттері, ал
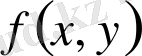 - бос мүшесі. Бұлар белгілі функциялар.
- бос мүшесі. Бұлар белгілі функциялар.
Ізделінді функция екі тәуелсіз айнымалыға байланысты анықталатын, екінші ретті сызықты дербес туындылы дифференциалдық теңдеудің жалпы түрі:
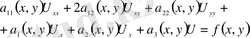 (1. 2. 3)
(1. 2. 3)
түрінде жазылады. Мұндағы
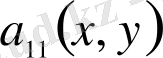 ,
,
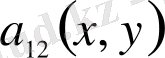 ,
,
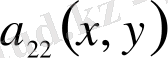 ,
,
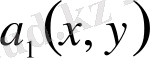 ,
,
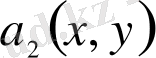
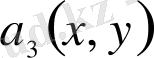 коэффициенттері және оң жағындағы
коэффициенттері және оң жағындағы
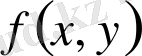 функциясы белгілі екі айнымалы функциялар. Егер (1. 2. 2) немесе (1. 2. 3) сызықты теңдеудің оң жағындағы
функциясы белгілі екі айнымалы функциялар. Егер (1. 2. 2) немесе (1. 2. 3) сызықты теңдеудің оң жағындағы
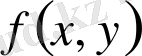 функциясы теңдеу қарастырылатын
функциясы теңдеу қарастырылатын
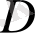 облысында нөлге тепе - тең болса, онда (1. 2. 2) немесе (1. 2. 3) теңдеуін
біртекті
, ал кері жағдайда, яғни
облысында нөлге тепе - тең болса, онда (1. 2. 2) немесе (1. 2. 3) теңдеуін
біртекті
, ал кері жағдайда, яғни
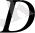 облысында
облысында
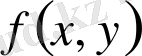 нөлге тең болмаса, онда
біртекті емес сызықты дербес туындылы дифференциалдық теңдеу
деп атайды.
нөлге тең болмаса, онда
біртекті емес сызықты дербес туындылы дифференциалдық теңдеу
деп атайды.
Екінші ретті сызықты дербес туындылы дифференциалдық теңдеулердің ішінде ерекше маңызды теңдеулер бар. Соларды атап өтейік:
1. Толқындық теңдеу (бірөлшемді)
 (1. 2. 4)
(1. 2. 4)
2. Жазықтықтағы толқындық теңдеу (екі өлшемді)
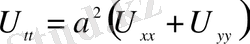 (1. 2. 5)
(1. 2. 5)
3. Кеңістіктегі толқындық теңдеу (үш өлшемді)
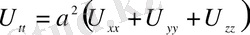 (1. 2. 6)
(1. 2. 6)
4. Жылуөткізгіштік теңдеуі (бірөлшемді)
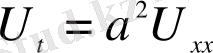 (1. 2. 7)
(1. 2. 7)
5. Жазықтықтағы жылуөткізгіштік теңдеуі (екі өлшемді)
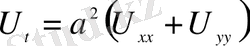 (1. 2. 8)
(1. 2. 8)
6. Кеңістіктегі жылуөткізгіштік теңдеуі (үш өлшемді)
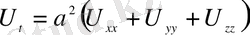 (1. 2. 9)
(1. 2. 9)
7. Жазықтықтағы Лаплас теңдеуі
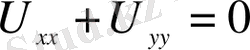 (1. 2. 10)
(1. 2. 10)
8. Кеңістіктегі Лаплас теңдеуі
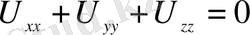 (1. 2. 11)
(1. 2. 11)
Тек осы теңдеулер негізгі математикалық физика теңдеулері болып табылады. Бұлар нақты физикалық процестің қарапайым моделіне сәйкес келеді. Біз 5 - ші тарауда осы теңдеулердің кейбіреулерін қорытып шығаруды және олардың шешімдерінің қасиеттерін қарастырамыз.
Дифференциалдық теңдеулерді зерттеген кезде оларды классификациялаған өте ыңғайлы, өйткені теңдеудің және оның шешімдерінің қасиеттері оның қандай класқа (типке) жататынына байланысты болады. Оларды әр түрлі белгілер арқылы классификациялауға болады.
Дифференциалдық теңдеулер сызықты, сызықты емес болып бөлінеді. Ізделінді функция мен оның туындыларының әр түрлі дәрежесі кіретін теңдеуді сызықты емес теңдеу деп атайды. Мысалы,
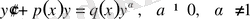
Бернулли теңдеуі - сызықты емес теңдеу.
Сызықты жай дифференциалдық теңдеу мен сызықты дербес туындылы дифференциалдық теңдеулердің кейбір ортақ қасиеттері бар. Сонымен бірге сызықты дербес туындылы дифференциалдық теңдеудің өзіне тән қасиеттері де болады.
Бірінші сызықты теңдеулердің ортақ қасиеттеріне тоқталып өтейік. Ол үшін сызықты дифференциалдық оператор ұғымын енгізейік. (1. 1. 4) - теңдеуін қарастырайық және осы теңдеудің сол жағын
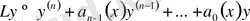 (1. 2. 12)
(1. 2. 12)
деп белгілейік.
(1. 2. 12) өрнегін
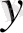 белгісіз функциясына байланысты
дифференциалдық оператор
деп атаймыз. Сызықты дифференциалдық оператор ұғымын сандық функцияның жалпыламасы ретінде түсінген жөн. Шынында да,
белгісіз функциясына байланысты
дифференциалдық оператор
деп атаймыз. Сызықты дифференциалдық оператор ұғымын сандық функцияның жалпыламасы ретінде түсінген жөн. Шынында да,
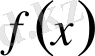 функциясы әрбір
функциясы әрбір
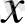 санына жаңа
санына жаңа
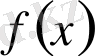 санын сәйкес қоятын болса,
санын сәйкес қоятын болса,
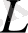 операторы әрбір
операторы әрбір
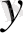 функциясына жаңа
функциясына жаңа
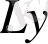 функциясын сәйкес қояды. Мысалы,
функциясын сәйкес қояды. Мысалы,
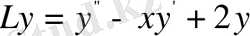 болсын. Онда
болсын. Онда
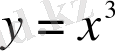 функциясы үшін
функциясы үшін
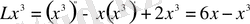 функциясын аламыз, яғни
функциясын аламыз, яғни
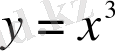 функциясына
функциясына
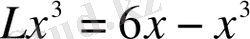 функциясы сәйкес қойылады. Дәл осы сияқты
функциясы сәйкес қойылады. Дәл осы сияқты
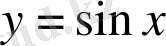 функциясына
функциясына
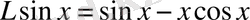 функциясы сәйкес қойылады.
функциясы сәйкес қойылады.
(1. 2. 2) және (1. 2. 3) теңдеулерінің сол жағын жоғарыдағы сияқты сәйкесінше
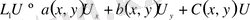 (1. 2. 13)
(1. 2. 13)
және
 (1. 2. 14)
(1. 2. 14)
деп белгілейік.
Сызықтық және сызықтық емес дифференциалдық теңдеулер ... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz