Санау жүйелері: позициялық принцип, негіздер, жүйелер арасындағы түрлендіру және арифметикалық операциялар


Санау жүйесі
Санау жүйесі бейпозициялық және позициялық принцип болып екіге бөлінеді.
Бейпозициялық санау жүйесінде символдың мәні сандағы орналасқан орнына байланысты емес. Бұл жүйенің мысалы ретінде римдік санау жүйесін алуға болады. Бұл жүйенің негізгі кемшілігі - символдар саны көп, олармен арифметикалық амалдар орындау өте күрделі. Бейпозициялық Санау жүйесіне қалдықтар класстарының жүйесі де жатады;
Сандарды белгілеудің ең жетілген принципі - позициялық принцип, онда бір санның таңбасы (цифр) орналасқан орнына байланысты әр түрлі мәнге ие болады. Позициялық санау жүйесі арифметикалық амалдар орындауға қолайлы, сондықтан оларды кеңінен пайдаланады. Мұндай Санау жүйесінде 1-разрядтың n бірлігі (Санау жүйесінің негізі) 2-разрядты бірлік, ал 2-разрядтың n бірлігі 3-разрядты бірлік, т. с. с. құрайды. 1-ден үлкен кез-келген сан Санау жүйесінің негізі бола алады. Мысалы: 757, 7 санында бірінші жеті саны 7 жүздікті, екіншісі - 7 бірлікті, ал үшіншісі - бірдің 7 ондық бөлігі.
700 + 50 + 7 + 0, 7 = 7 . 10 2 + 5 . 10 1 + 7 . 10 0 + 7 . 10 -1 = 757, 7.
Кез келген позициялық санау жүйесі өзінің негізімен сипатталады.
Нөлінші разряд кіші разряд деп аталады. Әрбір цифрға сандық балама (эквивалент) сәйкес келеді, А(р) жазуын енгіземіз. Ар жазуы - р жүйесіндегі саны n ак цифрден тұратын A санының сандық эквивалентін білдіреді (мұндағы к=0, 1 . . . n -I) . А санын цифрлардыңмына тізбегі түрінде көрсетуге болады.
A = a n-1 a n-2 . . . a 1 a 0 a -1 a -m
Бүл жағдайда үнемі а к < р теңсіздігі орындалады. Жалпы жағдайда, позициялық санау жүйесіндегі қандай да бір оң A санының сандық эквивалентін мына өрнекпен көрсетуге болады:
a n-1 q n-1 + a n-2 q n-2 + . . . + a 1 q 1 + a 0 q 0 + a -1 q -1 + . . . + a -m q -m ,
мұндағы,
q - санау жүйесінің негізгі, (бүтін он сан)
a i - берілген санау жүйесінің цифрасы.
n , m - санның үлкен разрядының нөмірі.
Мысалы:
Позициялық санау жүйесінде бүтін сандар қалай туындайды?
Әр бір санау жүйесінде сандар өз міндеріне қарай реттелген: 1 үлкен 0, 2 үлкен 1 және т. б.
1 цифрін өрлету оны 2 цифрін ауыстыру, 2 цифрін өрлету оны 3 цифрін ауыстыру деген мағынаны білдіреді. Үлкен цифрды өрлету мысалы 9 санын 0 санына ауыстыру деген мағына береді. Ал, екілік санау жүйесінде тек 0 және 1 сандары қолданылады, сондықтан 0 санын өрлету 1 санына ауыстыру дегенді немесе керісінше мағына береді.
Бүтін сандар кез келген санау жүйесінде Есептеу ережесі бойынша туындайды:
Осы ережені пайдалана отырып алғашқы он бүтін санды жазамыз:
- Екілік жүйеде: 0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001;
- Үштік жүйеде: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100;
- Бестік жүйеде: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14;
- Сегіздік жүйеде: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11.
Компьютермен маман қарым қатысты орнату үшін қандай санау жүйесін қолданады?
Ондық жүйеден басқа 2 санының бүтін дәрежесі болатын негіз бар жүйелер қолданылады, нақты айтсақ:
- Екілік(0, 1 цифрлары қолданылады) ;
- Сегіздік(0, 1, . . . , 7 цифрлары қолданылады) ;
- Оналтылық(алғашқы 0, 1, . . . , 9 цифрлары қолданылады, ал келесі сандар үшін - оннан он беске дейін - сан ретінде A, B, C, D, E, F символдары қолданылады) .
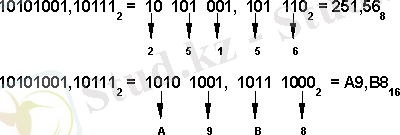
Мысалы:
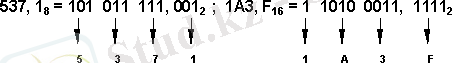
Мысалы,
Бүтін санды ондық жүйеден басқа позициялық санаужүйелерге қалай ауыстыруға болады?
Мысал: 75 санын ондық жүйеден екілік, сегіздік және он алтылық санау жүйелеріне ауыыстырып көрейік.
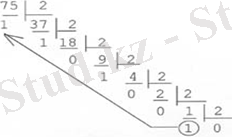
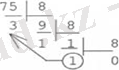
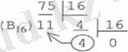
11 10 бірінші қалдық бұл мысалда он алтылық санау жүйесінде В 16 санымен бейнеленеді
Жауабы: 75 10 =1 001 011 2 = 113 8 = 4B 16 .
Ондық дүрыс бөлшекті кезкелген санау жүйесіне ауыстыру
Мысал. 0, 36 санын ондық жүйеден екілік, сегіздік және он алтылық санау жүйесіне ауыстырамыз:
36
2
72
2
44
2
88
2
76
2
36
8
88
8
04
8
36
16
76
16
Санды екілік (сегіздік, он алтылық) жүйеден ондық жүйеге қалай ауыстыру керек?
x q = (a n a n-1 . . . a 0 , a -1 a -2 . . . a -m ) q түріндегі q санау жүйесінде жазылған ( q = 2, 8 немесе 16) х санын ондық санау жүйесіне ауыстыру үшін
x 10 = a n q n + a n-1 q n-1 + . . . + a 0 q 0 + a -1 q -1 + a -2 q -2 + . . . + a -m q -m
көпмүшенің мәнін ондық арифметиканың көмегімен есептейміз.
Мысалдар:
Бүтін сандарды бір санау жүйесінен басқа санау жүйесіне аударудың қосымша кестесі
Компьютерде ғана қолданылатын - ондық, екілік, сегіздік және он алтылық санау жүйелерін қарастырайық. Мысалы 46 санын алайық және оған бір жүйеден екінші жүйеге барлық мүмкін болатын жүйелі ауыстыруларды орындайық. Ауыстыру ретін төмендегі суретке сай анықтаймыз:
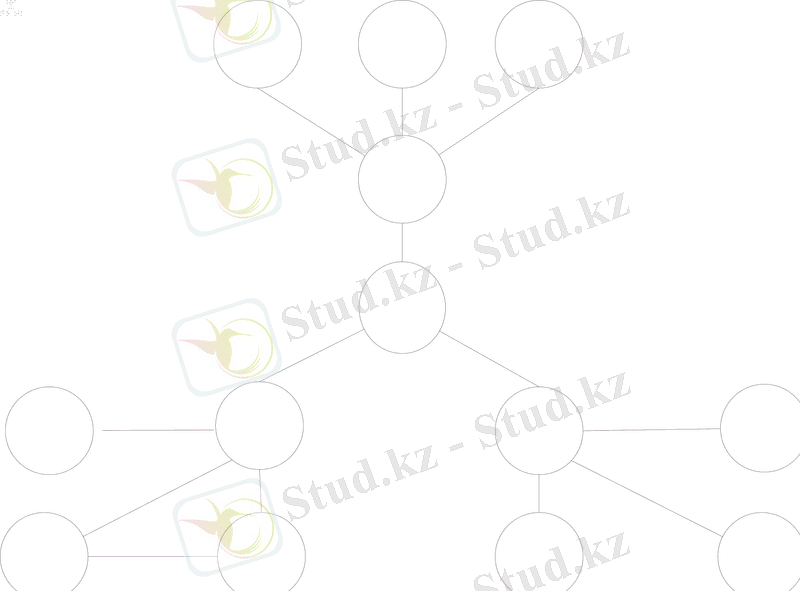
Мына суретте келесі белгілеулер қолданылған:
- Шеңберлерде негізгі санау жүйелері жазылған;
- Бағыттауыштар ауыстыру бағытын көрсетеді;
- Бағыттауыш жанындағы сан 1 кестесіндегі реттік санын көрсетіп тұр.
мысалы:
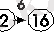 дегеніміз екілік санау жүйесінен он алтылық санау жүйесіне ауыстыру деген мағына білдіреді. Оның кестедегі реттік саны 6.
дегеніміз екілік санау жүйесінен он алтылық санау жүйесіне ауыстыру деген мағына білдіреді. Оның кестедегі реттік саны 6.
Бүтін сандарды аударудың қосымша кестесі
Кесте 1.
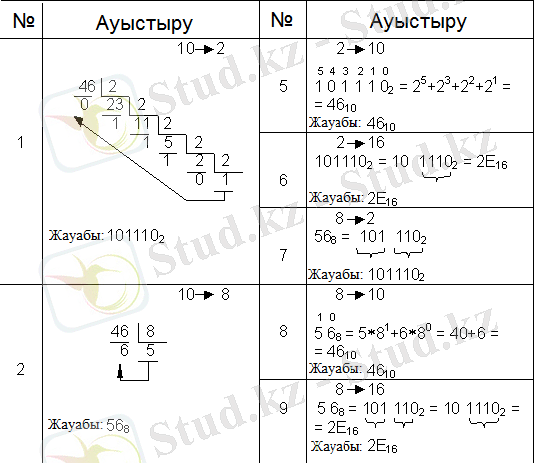
Кесте2.

Негізгі арифметикалық операциялар - қосу, азайту, көбейту және бөлу.
Қ О С УЕкілік санау жүйесінде қосу кестесі

Сегіздік санау жүйесінде қосу кестесі
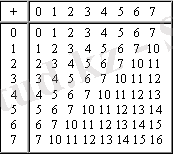
Он алтылық санау жүйесінде қосу кестесі

Қосу кезінде сандар разряд бойынша қосылады да, және егер артық шықса, солға қарай өтеді.
Мысал 1. 15 және 6 сандарын әртүрлі санау жүйесінде қосып көрейік.
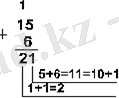
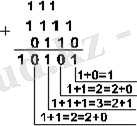
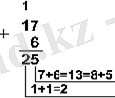
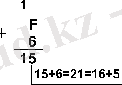
Жауабы:
15+6 = 21
10
= 10101
2
= 25
8
= 15
16
.
Тексеру.
Алынған қосындыларды ондық жүйеге ауыстырамыз:
10101
2
= 2
4
+ 2
2
+ 2
0
= 16+4+1=21
25 8 = 2 . 8 1 + 5 . 8 0 = 16 + 5 = 21,
15 16 = 1 . 16 1 + 5 . 16 0 = 16+5 = 21.
Мысал 2. 15 10 , 7 10 және 3 10 сандарын әртүрлі санау жүйесінде қосып көрейік
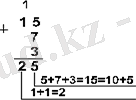
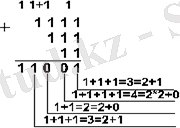
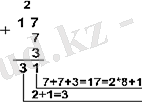
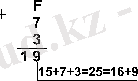
Жауабы: 5+7+3 = 25 10 = 11001 2 = 31 8 = 19 16 .
Тексеру: Алынған нәтижені ондық санау жүйесіне ауыстырамыз:
11001 2 = 2 4 + 2 3 + 2 0 = 16+8+1=25,
31 8 = 3 . 8 1 + 1 . 8 0 = 24 + 1 = 25,
19 16 = 1 . 16 1 + 9 . 16 0 = 16+9 = 25.
Мысал 3. 141, 5 және 59, 75 сандарын қосайық.

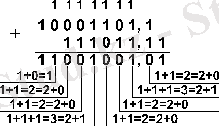
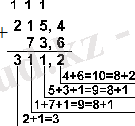
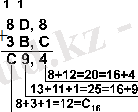
Жауабы: 141, 5 + 59, 75 = 201, 25 10 = 11001001, 01 2 = 311, 2 8 = C9, 4 16
Тексеру. Алынған нәтижені ондық санау жүйесіне ауыстырамыз::
11001001, 01 2 = 2 7 + 2 6 + 2 3 + 2 0 + 2 -2 = 201, 25
311, 2 8 = 3 . 8 2 + 18 1 + 1 . 8 0 + 2 . 8 -1 = 201, 25
C9, 4 16 = 12 . 16 1 + 9 . 16 0 + 4 . 16 -1 = 201, 25
АЗАЙТУ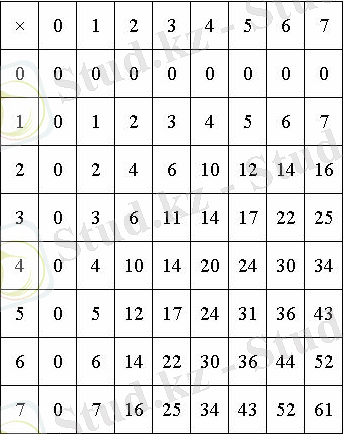
Мысал 4. 10 2 , 10 8 және 10 16 сандарынан 1 санын азайтайық.
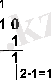
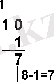
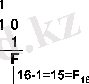
Мысал 5. 100 2 , 100 8 және 100 16 сандарынан 1 санын азайтайық.
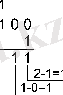
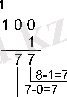
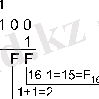
Мысал 6. 201, 25 санынан 59, 75 санын аламыз.
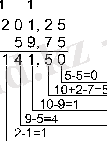
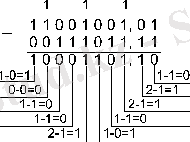
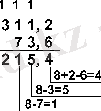
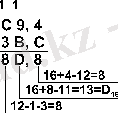
Жауабы: 201, 25 10 - 59, 75 10 = 141, 5 10 = 10001101, 1 2 = 215, 4 8 = 8D, 8 16 .
Тексеру. Алынған нәтижені ондық санау жүйесіне ауыстырамыз:
10001101, 1 2 = 2 7 + 2 3 + 2 2 + 2 0 + 2 -1 = 141, 5;
215, 4 8 = 2 . 8 2 + 1 . 8 1 + 5 . 8 0 + 4 . 8 -1 = 141, 5;
8D, 8 16 = 8 . 16 1 + D . 16 0 + 8 . 16 -1 = 141, 5.
КӨБЕЙТУЕкілік санау жүйесінде көбейту

Сегіздік санау жүйесінде көбейту
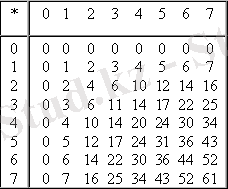
Мысал 7. 5 және 6 сандарын көбейтейік.
X 5
6 f
30
101
X 110
101
101 1
0
X 5
6 f
36
Жауабы: 5 . 6 = 30 10 = 0 2 = 36 8 .
Тексеру. Алынған нәтижені ондық санау жүйесіне ауыстырамыз::
0 2 = 2 4 + 2 3 + 2 2 + 2 1 = 30;
36 8 = 3*8 1 + 6*8 0 = 30.
Мысал 8. 115 және 51 сандарын көбейтеміз.
X 115
51
115
575 1
5865
X 1110011
110011
1110011
1110011
1110011 1
1011011101001
X 163
63
531
12621
13351
Жауабы: 115 . 51 = 5865 10 = 1011011101001 2 = 13351 8 .
Тексеру. Алынған нәтижені ондық санау жүйесіне ауыстырамыз:
1011011101001 2 = 2 12 + 2 10 + 2 9 + 2 7 + 2 6 + 2 5 + 2 3 + 2 0 = 5865;
13351 8 = 1 . 8 4 + 3 . 8 3 + 3 . 8 2 + 5 . 8 1 + 1 . 8 0 = 5865.
БӨЛУМысал 9. 30 санын 6 санына бөлейік.
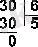
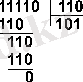
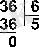
Жауабы: 30 : 6 = 5 10 = 101 2 = 5 8 .
Мысал 10. 5865 санын 115 санына бөлейік.



Жауабы: 5865 : 115 = 51 10 = 110011 2 = 63 8 .
Тексеру. Алынған нәтижені 10 санау жүйесіне ауыстырамыз:
110011 2 = 2 5 + 2 4 + 2 1 + 2 0 = 51;
63 8 = 6 . 8 1 + 3 . 8 0 = 51.
Мысал 11. 35 санын 14 санына бөлейік



Жауабы: 35 : 14 = 2, 5 10 = 10, 1 2 = 2, 4 8 .
Тексеру. Алынған нәтижелерді ондық жүйеге ауыстырып көрейік:
10, 1 2 = 2 1 + 2 -1 = 2, 5;
2, 4 8 = 2 . 8 0 + 4 . 8 -1 = 2, 5.
Тапсырмалар
№1 тапсырма. Сандарды қосуды орындау
+101+1000 =
+1011+10101=
ED45C+4F56=
32C+AF12=
100011+1101=
1011011+1011+10001=
1C4D+24F=
23DF+EF15=
110011001+111=
1010+110001+1011=
24CA+5B3A=
7B3F+1CFD=
10110100+1110011=
Н 101000+1100+111=
7B3F+5B3A=
1C4D+EF15=
10101I+101I01=
11011011+11001101+11011=
ED45C+AF12=
24CA+24CA=
1001001+101=
++=
B0FD+C1E8=
BCD8+5DE4=
1011011+111=
11+11+11=
ACD6+F5C7=
EF15+24CA=
11010001+101010=
100010001+111+10101=
F5C7+IC4D=
9CFD+6F3F=
11101101+1110110=
1011+1001001+01=
EF15+6DA7=
3EF9+ECFA=
110011001+111=
++=
24CA+5B3A=
BCD8+5DE4=
10100011+11011001=
11101+1101011=
А591+С16=
1F5A+4D6=
0110011+1101101001001
0110011+1010111011101
4D16+ F5C7=
AF12+24CA =
№2 тапсырма.
Мысалы: 1010011І3= 167
1*2 7 + 0*2 6 + 1*2 5 + 0*2 4 + 0*2 3 + 1*2 2 + 1*2 1 + 1*2 0 = 128+0+32+0+01 +4+2+1 = 167
Мысалы: е4с15 16 = 1110010011010101 2
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz