ЭЕМ арифметикалық негіздері: санау жүйелері, кодтау және сандық көрсетілімдер


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:
Қазақстан Республикасы Білім және Ғылым Министрлігі
Семей қаласының Шәкәрім атындағы мемлекеттік университеті
Автоматика және электротехника кафедрасы
СӨЖ
Тақырыбы: ЭЕМ арифметикалық негіздері. ЭЕМ-де ақпаратты көрсету
.
Орындаған: Жапар Ботагөз
Тобы: ВТ-305
Қабылдаған: Адылканова А. Ж
Семей 2015 ж
7 Дәріс.
Тақырыбы: ЭЕМ арифметикалық негіздері. ЭЕМ-де ақпаратты көрсету. Мақсаты: Пәннің мазмұнымен таныстыру.
Дәріс сұрақтары.
1. Санау жүйелері.
2. Сандарды бір позициялық санау жүйесінен екінші жүйеге аудару.
3. Теріс сандарды кодалау. Тура, кері қосымша кодтар.
ЭЕМ-де кез келген ақпарат мына түрлердің бірінде беріледі:
- Екілік санау жүйесінде;
- Ондық санау жүйесінде;
- Он алтылық санау жүйесінде;
- Символдық түрде;
- Графикалық формада.
Санау жүйелері . Цифрлық есептеуіш техника сандарды өрнектеудің әр түрлі тәсілдерін пайдаланады. Кез келген санды қайсы бір символдар (цифрлар) алфавитімен өрнектеу тәсілі санау жүйесі (римдік, арабтық) деп аталады. Егер бір ғана цифр (символ) санды кескіндейтін цифрлар тізбегіндегі өзінің позициясына байланысты әр түрлі мәнге ие болса, онда мұндай жүйені позициялық санау жүйесі деп атайды. Ең қарапайым позициялық санау жүйесі не ондық жүйе мысал бола алады. Бұл жүйедегі 77, 7 санының үтірден кейінгі 7 цифр оннан жеті бөлікті, үлкен разрядтағы 7-ондық білдіріледі. Позициялық санау жүйесіндегі сандарды жазуға қолданылатын әр түрлі цифрлар санын санау жүйесінің негізгі немесе базисі деп атайды.
Позициялық емес санау жүйесінде сандағы символдар (цифрлар) мәні оның позициясына байланысты болмайды. Позициялық емес санау жүйесіне
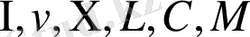 және т. б. символдарды пайдаланатын римдік жүйе жатады. Позициялық жүйеде
және т. б. символдарды пайдаланатын римдік жүйе жатады. Позициялық жүйеде
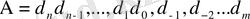 аралас санын мынадай полином түрінде көрсетуге болады:
аралас санын мынадай полином түрінде көрсетуге болады:
 мұнда
мұнда
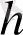 - санау жүйесінің негізі,
- санау жүйесінің негізі,
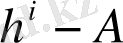 санындағы
i
-разрядтың салмағы,
санындағы
i
-разрядтың салмағы,
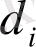 - санау жүйесіндегі цифрдан түратын коэффицент. Ең көп таралған санау жүйесіне екілік, ондық, сегіздік және оналтылық санау жүйелерін жатқызуға болады.
А
саны өрнектелетін санау жүйесін көрсету үшін сан жанына қойылатын төменгі индексті пайдаланады;
А
h.
Ондық санау жүйесінің негізгі
h=10
. сандарды жазып көрсету үшін
0
-ден
9
-ға дейінгі
10
әр түрлі бүтін цифрлар (араб цифрлары) қолданылады. Есептеулерді орындау ережелері қосу және көбейту кестелері арқылы анықталады.
- санау жүйесіндегі цифрдан түратын коэффицент. Ең көп таралған санау жүйесіне екілік, ондық, сегіздік және оналтылық санау жүйелерін жатқызуға болады.
А
саны өрнектелетін санау жүйесін көрсету үшін сан жанына қойылатын төменгі индексті пайдаланады;
А
h.
Ондық санау жүйесінің негізгі
h=10
. сандарды жазып көрсету үшін
0
-ден
9
-ға дейінгі
10
әр түрлі бүтін цифрлар (араб цифрлары) қолданылады. Есептеулерді орындау ережелері қосу және көбейту кестелері арқылы анықталады.
Екілік санау жүйесінің негізгі h=2 , ол 10 2 түрінде (екілік санау жүйсінде) жазылады. Екілік жүйеде екі цифр - 0 және 1 қолданылады. Арифметикалық амалдар екілік жүйеде төменде көрсетілген ережелер арқылы орындалады.
Екілік қосу
0+0=0
0+1=1
1+0=1
1+1=10
Екілік азайту
0-0=0
1-0=1
1-1=0
10-1=1
Екілік көбейту
0*0=0
0*1=0
1*0=0
1*1=1
Сегіздік санау жүйесінің негізгі h=8, ол 10 8 түрінде жазылады. Жүйеде 8 ондық цифрлар қолданылады: 0, 1, 2, 3, 4, 5, 6, 7. арифметикалық амалдарды қосу және көбейту кестелеріне сәйкес орындалады (2. 11 және 2. 12-кестелер) .
2. 11 - кесте
0
1
2
3
4
5
6
7
10
0
1
2
3
4
5
6
7
10
1
2
3
4
5
6
7
10
11
2
3
4
5
6
7
10
11
12
3
4
5
6
7
10
11
12
13
4
5
6
7
10
11
12
13
14
5
6
7
10
11
12
13
14
15
6
7
10
11
12
13
14
15
16
7
10
11
12
13
14
15
16
17
10
11
12
13
14
15
16
17
20
Оналтылық санау жүйесінде h=16 , ол 10 16 түрінде жазылады. Бірінші он символдарды белгілеу үшін ондық жүйеде қолданылатын 10 цифр пайдаланылады, ал 10, 11, 12, 13, 14, 15 мәндерін белгілеу үшін латын алфавитінің алғашқы алты әрпі қолданылады: А, В, С, Д, Е, F .
2. 12 - кесте
0
1
2
3
4
5
6
7
10
0
0
0
0
0
0
0
0
0
0
1
2
3
4
5
6
7
10
0
2
4
6
10
12
14
16
20
0
3
6
11
14
17
22
25
30
0
4
10
14
20
24
30
34
40
0
5
12
17
24
31
36
43
50
0
6
14
22
30
36
44
52
60
0
7
16
25
34
43
52
61
70
0
10
20
30
40
50
60
70
100
Оналтылық жүйеде қосу және көбейту амалдарын орындау үшін 2. 11 және 2. 12-кестелері пайдаланылады.
Сандарды бір позициялық санау жүйесінен екінші жүйеге аудару. Цифрлық автоматтарда түрлі санау жүйелері қолданылатын болғандықтан сандарды бір жүйеден екінші жүйеге аудару қажеттігі туып отырады. Сандарды бір жүйеден екінші жүйеге аударудың бірнеше тәсілдері бар. Ең қарапайым тәсіл баламалар кестелеріне негізделген. Бұл тәсіл тек санау жүйесінің негіздері q мен h бір бірімен q=h k ( k>1 -бүтін сан) тәуелділігінде болған жағдайда ғана қолданылады. Сандарды бір жүйеден екінші жүйеге аудару бастапқы жүйе цифрларының әрқайсысын оның жаңа санау жүйесіндегі баламаларымен ауыстыруарқылы іске асырады.
q=h k шарты орындалмаған жағдайда санның бүтін бөлігін жаңа санау жүйесінің негізін q -ға бөлуге және бөлшек бөлігін осы негізге көбейтуге негізделген басқа тәсіл қолданылады. Санның бүтін бөлігін аудару үшін оны және бөлгеннен кейін алынған бөліндіні біртіндеп (тізбектеп) жаңа санау жүйесінің негізгі q -ға кезекті бөлінді q -дан кем болғанша бөлінеді. Алынған ретінде кері жазылған соңғы бөлінді мен қалдықтар тізбегі санның бүтін бөлігінің жаңа санау жүйесіндегі мәнін береді. Бұл жерде мынаны ескерген жөн. Санды жаңа негізге бөлгенде арифметикалық амалдар бастапқы санау жүйесінде жүргізіледі, іздеп отырған санның цифрлары да осы жүйеде алынып, олар жаңа санау жүйесінің эквиваленттерімен ауыстырылады.
Санның бөлшек бөлігін аудару үшін оны және көбейткеннен кейін алынған кезекті бөлшекті жаңа санау жүйесінің негізгі q -ға біртіндеп (тізбектеп) көбейту керек. Көбейтілгеннен кейінгі алынған бүтін бөліктер негізгі q болатын санау жүйесіндегі санның бөлшек бөлігі болады. Көбейтулер саны алынатын нәтиженің керекті дәлдігімен анықталады.
Сандарды бір жүйеден екінші жүйеге полином түрінде көрсету арқылы аударуға болады. Кез келген
А=a
n
a
n-1…
a
1
a
0
a
-1
a
-2…
a
-m
саны
 өрнектеледі, мұнда берілген санның бастапқы негізі,
өрнектеледі, мұнда берілген санның бастапқы негізі,
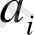 -санау жүйесіндегі цифрлар.
-санау жүйесіндегі цифрлар.
Негізі
q
болатын санау жүйесіндегі
А
санын басқа жүйеге аудару үшін баламалар кестесіне сәйкес полиномдағы
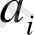 және
h
цифрларын олардың
q
жүйесіндегі баламалармен ауыстырып, тиісті амалдарды
q
санау жүйесінде орындау керек.
және
h
цифрларын олардың
q
жүйесіндегі баламалармен ауыстырып, тиісті амалдарды
q
санау жүйесінде орындау керек.
Қазіргі цифрлық машиналарында негізі 2, 8, 16 болатын және екілі-ондық позициялы санау жүйелері кеңінен қолданылады. Мамандандырылған және арнаулы машиналар басқа да санау жүйелері қолданылады (қалдықтар кластары, молдық санау жүйелері т. б. ) .
Сандарды көрсету формасы.ЦЕМ- де сандық мәліметтерді көрсету үшін сандардың табиғи және қалыпты жазылу түрлері қолданылады.
Бірінші жағдайда сан табиғи түрде жазылады: 1750; 14, 85; 0, 003572 және т. с. с. сандарды өңдеуге ыңғайлы болу үшін үтір (нүкте) машинаның разряд торының белгілі бір жеріне қатаң тиянақталып қойылады да бұлай жазылу санның тиянақты үтірлі (нүктелі) өрнектелуі деп аталады. Әдетте нүкте (үтір) разряд түрінде жоғарғы разрядтың алдында (2. 31, а-сурет) не төменгі разрядтың соңында (2. 31, ә-сурет) тиянақталады. Бірінші жағдайда санның модулі бірден аз, ал екінші жағдайда - сан бүтін болады. Сандардың таңбасын көрсету үшін әдетте ЭЕМ разряд торында жеке разряд бөлінеді (ол 2. 31-суретте көрсетілгеней сол жақ шекті разряд) ; оң сан көрсетілсе, таңба разрядына 0 жазылады, ал теріс сан көрсетілсе, ол разрядқа 1 жазылады. Егер үтір (нүкте) төменгі разрядтан кейін тиянақталса (бүтін сан), нольден ерекше ең кіші модульді сан А min =1 , ал ең үлкен модульді сан А max =2 n -1 болады, онда сандарды көрсету арқылы 1≤/А/≤2 n -1 түрінде табылады. Егер үтір (нүкте) жоғарғы разрядтың алдында тиянақталса, онда А саны мына ауқымда өрнектеледі: 2 -n ≤/А/≤1-2 n . іс жүзінде қазір ЦЕА-де тиянақты үтір үшін сандарды бүтін түрде өрнектеу қолданылады. 1 және 2-буынды ЦЕА-де тиянақты үтір үшін сандарды дұрыс бөлшек түрінде өрнектеу қолданылады.
Қалыпты жазылу жағдайында бір сан әр түрде өрнектелуі мүмкін: 1750=175. 10 1 =1, 75. 10 3 =0, 175. 10 4 және т. с. с. жалпы түрде
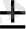
2. 31-сурет
а)
Мантица рет таң- рет мантисса
Таңбасы басы модулі модулі(оналтылық)
ә)
Мантица рет таң- рет мантисса
Таңбасы басы модулі модулі(оналтылық)
б)
Мантица азытқыған мантисса
Таңбасы рет (оналтылық)
2. 32-сурет
2. 33-сурет
Бұл жазылуды
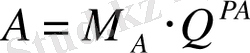 етіп өрнектеуге болады, бұл жерде
М
А
-санның мантиссасы,
Р
А
-
санның реті (бүтін сан),
Q
-мантисса жазылатын санау жүйесінің негізіне дәлме-дәл келетін өрнектеу параметрі. Нақтылы машина үшін
Q
параметрі тұрақты шама болатындықтан, ол машинаның разряд торында жазылмайды.
А
саны шартты түрде машинада былай көрсетіледі:
етіп өрнектеуге болады, бұл жерде
М
А
-санның мантиссасы,
Р
А
-
санның реті (бүтін сан),
Q
-мантисса жазылатын санау жүйесінің негізіне дәлме-дәл келетін өрнектеу параметрі. Нақтылы машина үшін
Q
параметрі тұрақты шама болатындықтан, ол машинаның разряд торында жазылмайды.
А
саны шартты түрде машинада былай көрсетіледі:
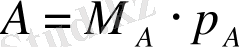 . өрнектеудің бұл түрінде үтір қатаң тиянақталмағандықтан, ол сандарды жылжымалы үтір (нүктелі) өрнектеу деп аталады. Мантисса
/М
А
/<1
, яғни дұрыс бөлшек болады. Санның реті
Р
А
оң және теріс бүтін сан болуы мүмкін, ол А санындағы үтірдің орнын анықтайды, екілік сан үшін
. өрнектеудің бұл түрінде үтір қатаң тиянақталмағандықтан, ол сандарды жылжымалы үтір (нүктелі) өрнектеу деп аталады. Мантисса
/М
А
/<1
, яғни дұрыс бөлшек болады. Санның реті
Р
А
оң және теріс бүтін сан болуы мүмкін, ол А санындағы үтірдің орнын анықтайды, екілік сан үшін
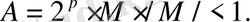 әдетте ЭЕМ-де жылжымалы үтірлі сандар өрнектелгенде мантиссаның жоғарғы разрядында 1 түрады, яғни
2
-1
≤/М/≤1
. бұндай сандарды қалыптыланғын деп атайды. Мысалы: 0. 110111. (2
010
) - қалыптыланған сан. Қалыптыланбаған санға мысал - 0. 0111011. (2
001
) . Бұдан қалыптыланған сан алу үшін мантиссаны солға қарай бір разряд жылжытамыз да ретін бірге кемітеміз. Сонда жоғарыдағы санды мына түрде жазуға болады: 0. 110 110(2
010
) .
әдетте ЭЕМ-де жылжымалы үтірлі сандар өрнектелгенде мантиссаның жоғарғы разрядында 1 түрады, яғни
2
-1
≤/М/≤1
. бұндай сандарды қалыптыланғын деп атайды. Мысалы: 0. 110111. (2
010
) - қалыптыланған сан. Қалыптыланбаған санға мысал - 0. 0111011. (2
001
) . Бұдан қалыптыланған сан алу үшін мантиссаны солға қарай бір разряд жылжытамыз да ретін бірге кемітеміз. Сонда жоғарыдағы санды мына түрде жазуға болады: 0. 110 110(2
010
) .
Разряд торында бір мәнді өрнектелетін санның ауқымды мына теңсіздікпен анықталады: А min ≤/A/≤A max , мұнда А min және A max санның өнектелу түрін ескергендегі алынған ең үлкен және ең кіші мәндер. Жылжымалы үтірлі түрде берілген санның өрнектелу ауқымы сан мантиссасының /М А /, ретінің /Р А /, Q параметрінің өрнектелу ауқымдарына байланысты есептеледі.
Модулі бойынша ең кіші жылжымалы үтірлі сан салмағы
2
-1
-не тең жоғарғы разрядқа жазылған бірмен
/М
min
=2
-1
/
және абсолют шамасы бойынша ең үлкен теріс ретпен
/-Р=-(2
k
-1) /
өрнектеледі. Сонда:
А
min
=
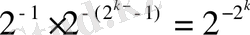 ,
мұнда
k
-реттің разряды. Модулі бойынша ең үлкен жылжымалы үтірлі сан
A
max
=М
max
,
мұнда
k
-реттің разряды. Модулі бойынша ең үлкен жылжымалы үтірлі сан
A
max
=М
max
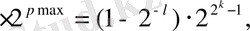 мұнда l - мантиссаның разряды, сонда жылжымалы үтірлі санның өрнектелу ауқымы
мұнда l - мантиссаның разряды, сонда жылжымалы үтірлі санның өрнектелу ауқымы
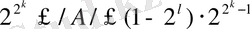
2. 32, а-суретте
Q=2, k=6, l=24
болғанда ЭЕМ-де жылжымалы үтірлі сандарды өрнектеу келтірілген. Бұл жерде
A
max
=
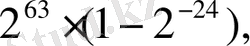 А
min
=
А
min
=
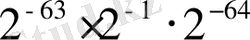 .
Разряд торында мантисса таңбасын ескере отырып (2. 32, а-сурет),
.
Разряд торында мантисса таңбасын ескере отырып (2. 32, а-сурет),
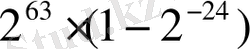 -нен -
2
-64
-не дейінгі және
+2
-64
-нен
+2
63
-не дейінгі ауқымда жататын сандарды өрнектеуге болады, бұл абсолют шамалар үшін сандардың
10
-19
-нен
10
+19
-не дейінгі ауқымына сәйкес келеді. Келтірілген ауқым сол 32 разрядты сөзде өрнектелген жылжымалы үтірлі сандардың ауқымынан жоғары.
-нен -
2
-64
-не дейінгі және
+2
-64
-нен
+2
63
-не дейінгі ауқымда жататын сандарды өрнектеуге болады, бұл абсолют шамалар үшін сандардың
10
-19
-нен
10
+19
-не дейінгі ауқымына сәйкес келеді. Келтірілген ауқым сол 32 разрядты сөзде өрнектелген жылжымалы үтірлі сандардың ауқымынан жоғары.
Қазіргі жалпы мақсатты ЭЕМ-де жылжымалы үтірлі сандар негізі екінің бүтін дәрежесі болатын
(Q=2
-y
)
санау жүйесінде өрнектеледі:
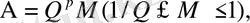 мұнда
Р
-екілік бүтін сан, мантисса М екілік
y
разрядты топтар мантисса цифрларын негізгі
Q=2
y
болатын санау жүйелерінде бейнелейтіндей санмен өрнектеледі. ЭЕМ БЖ (электрондық есептеуіш машиналардың біртұтас жүйелерінде) жылжымалы үтірлі сандар оналтылық санау жүйесінде көрсетіледі (2. 32, б-сурет) :
мұнда
Р
-екілік бүтін сан, мантисса М екілік
y
разрядты топтар мантисса цифрларын негізгі
Q=2
y
болатын санау жүйелерінде бейнелейтіндей санмен өрнектеледі. ЭЕМ БЖ (электрондық есептеуіш машиналардың біртұтас жүйелерінде) жылжымалы үтірлі сандар оналтылық санау жүйесінде көрсетіледі (2. 32, б-сурет) :
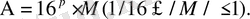 Р
ретінің модулі бүтін алты разрядты екілік санмен бейнеленеді, ал мантисса
М
-оналтылық сандардан құралған сан ретінде қарастырылады. Жылжымалы үтірлі санның жоғары оналтылық цифры (2. 32, б-суретте 8+11 разрядтар) 0-ден ерекше болса, онда оны қалыптыланған сан деп есептейді. Қарсы жағдайда мантиссаны сол жаққа қарай
n
оналтылық разрядқа жылжыту арқылы сан қалыптыланады және осыған сәйкес санның реті
n
бірлікке кемиді (мантиссаны бір оналтылық разрядқа жылжыту мантиссаны төрт екілік разрядқа жылжытуға сәйкес келеді) .
Р
ретінің модулі бүтін алты разрядты екілік санмен бейнеленеді, ал мантисса
М
-оналтылық сандардан құралған сан ретінде қарастырылады. Жылжымалы үтірлі санның жоғары оналтылық цифры (2. 32, б-суретте 8+11 разрядтар) 0-ден ерекше болса, онда оны қалыптыланған сан деп есептейді. Қарсы жағдайда мантиссаны сол жаққа қарай
n
оналтылық разрядқа жылжыту арқылы сан қалыптыланады және осыған сәйкес санның реті
n
бірлікке кемиді (мантиссаны бір оналтылық разрядқа жылжыту мантиссаны төрт екілік разрядқа жылжытуға сәйкес келеді) .
Оналтылық жүйеде келтірілген (2. 32, б-сурет) қалыптыланған сан-
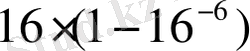 -нен
-+16
-64
-
не дейінгі және
+16
-64
-нен
-нен
-+16
-64
-
не дейінгі және
+16
-64
-нен
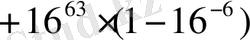 -не дейінгі ауқымда жатады; бұл сандардың модульдері үшін
10
-77
-нен
10
76
-не дейінгі ауқымға сәйкес келеді. Сонымен жылжымалы үірлі сандарды оналтылық санау жүйесінде өрнектеу екілік санау жүйесіне қарағанда сандардың едәуір үлкен ауқымын алуға мүмкіндік береді.
-не дейінгі ауқымда жатады; бұл сандардың модульдері үшін
10
-77
-нен
10
76
-не дейінгі ауқымға сәйкес келеді. Сонымен жылжымалы үірлі сандарды оналтылық санау жүйесінде өрнектеу екілік санау жүйесіне қарағанда сандардың едәуір үлкен ауқымын алуға мүмкіндік береді.
Теріс сандарды кодалау. Тура, кері қосымша кодтар.
G саны жалпы түрде ЭВМ-де былай көрсетіледі:
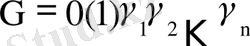 ,
,
мұндағы 0(1) - санның таңбасы, 0 = “+” таңбаны, 1 = “-” таңбаны білдіреді.
ЦЕМ-да санды өңдеудің ыңғайлылығы үшін тура, кері және қосымша код деген түсініктер енгізілген (процессордың (қосындылағыштың) бір ғана арифметикалық операция - қосу операциясын орындайтынын ескере отырып) .
Оң сандар үшін:
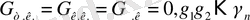
теріс сандар үшін:
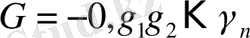
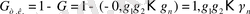
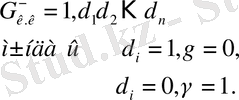
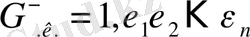
0, ε 1 ε 2 …ε n - санның бүтін бөлігін 1 модульге дейін толықтыру.
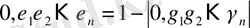
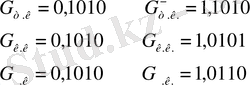
Тиянақты үтірлі сандарды қосындылау мен азайту
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz