Салыстырулар теориясының негізі

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 3
1 САЛЫСТЫРУЛАР ТЕОРИЯСЫНЫҢ НЕГІЗІ ... ... ... ... ... ... ... ... ... ... ... . 5
1.1 Салыстырулар және бірінші дәрежелі салыстырулардың
негізгі қасиеттері ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 5
1.2 Жоғары дәрежелі салыстырулардың ерекше қасиеттері ... ... ... ... ... ... ... 19
ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 20
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 21

Сандардың элементар теориясының маңызды мәселелерінің бірі болып табылатын салыстырулар теориясының негізіне тоқталайық. Салыстыру жөніндегі ұғым, мұны ең алғаш рет қолданған Гаусс, бір санның екінші санға бөлінгіштігі ұғымымен тығыз байланысты. Бұл ұғым бізге әсіресе берілген сандардың бірі екіншісіне бөлінетін-бөлінбейтінін және де қандай қалдық қалатынын білу керек болғанда аса қажет болмақ.
Алгебра және сандар теориясын оқу барысында мектеп матемтикасымен тығыз байланысты көптеген тақырыптар қарастырылады. Арифметикадағы қосу, алу, көбейту, бөлу амалдары математикалық объектілер жиынындағы алгебралық операциялар болып жалпыланады. Арифметикадағы қалдықты бөлу, сандардың бөлінгіштігі, үлкен,кіші, тағы басқа ұғымдар, геометриядағы фигуралардың ұқсастығы, түзулердің параллельдігі, перпендикуляр болуы,тағы басқа ұғымдар бинарлық қатынастың дербес жағдай екендігі көрсетіледі. Нөлдің қасиеті, таңбалар ережесі минуспен байланысты амалдардың басқа қасиеттері мектеп математикасында дәлелдеусіз беріледі. Топтар, сақина, өріс тақырыптары үйрену кезінде бұл қасиетердің барлығы және жақша ашу ережелері дәлелдеумен беріледі.
Сандардың элементар теориясының маңызды мәселедерінің бірі болып табылатын салыстырулар теориясының негізіне тоқталайық. Салыстыру жөніндегі ұғым, мұны ең алғаш рет қолданған Гаусс, бір санның екінші санға бөлінгіштігі ұғымымен тығыз байланысты. Бұл ұғым бізге әсіресе берілген сандардың бірі екіншісіне бөлінетін-бөлінбейтінің және де қандай қалдық қалатынын білу керек болғанда аса қажет болмақ.
Мысалы, -натурал сан болғанда, мәнін табу үшін біз дәреже -ді әдетте -ке бөлеміз де, тек қалдыққа ғана назар аударамыз.
Егер де
болса,
онда болады.
Ал енді мәнін табу керек болғанда да -тың -қаеселігін ескермей, тек қалдықты ғана алмыз.
Бұл сияқты есептерді шешкенде салыстырулар теориясының көптеген жеңілдік туғызатынын байқаймыз.
Айталық -алдын ала белгіленген бүтін оң сан делік.Былайғы жерде мұны біз салыстыру модулы деп атайтын боламыз. Егер (не ) айырмасы санына бөлінетін болса, онда бүтін мен екі сан модулы бойынша өзара салыстырымды делінеді .
Гаусс қолданған белгілеу бойынша саны санымен салыстырымды. мен сандары салыстыру мүшелері деп аталады. Мысалы, мен сандары модулы бойынша өз ара салыстырымды：

1. Оразбаев Б.М. Сандар теориясы.- Алматы.: «Мектеп» 1970ж.
2. Завало С.Т. Алгебра и теория чисел.2 часть.-Киев.: «Высшая школа» 1980ж.
3. Омаров Р. Алгебра және сандар теориясы. 1 Бөлім.(әдістемелік нұсқау).- Алматы.: Республикалық баспа кабинеті 1992ж.
4. Казачек Н.А., Виленкин.Н.Я. Алгебра и теория чисел.- Москва.: «МГЗПИ» 1984ж.
5. Н.Н. Признаки делимости.- Москва.: «Наука» 1988ж.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

МАЗМҰНЫ
КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... ... ... ... ... ... .. 3
1 САЛЫСТЫРУЛАР ТЕОРИЯСЫНЫҢ
НЕГІЗІ ... ... ... ... ... ... ... . ... ... ... ... 5
1.1 Салыстырулар және бірінші дәрежелі салыстырулардың
негізгі
қасиеттері ... ... ... ... ... ... . ... ... .. ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... .. 5
1.2 Жоғары дәрежелі салыстырулардың ерекше
қасиеттері ... ... ... ... ... ... . ... 19
ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
... ... ... ... ... ... ... ... ... ... ... 20
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР
ТІЗІМІ ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 21

КІРІСПЕ

Сандардың элементар теориясының маңызды мәселелерінің бірі болып
табылатын салыстырулар теориясының негізіне тоқталайық. Салыстыру жөніндегі
ұғым, мұны ең алғаш рет қолданған Гаусс, бір санның екінші санға
бөлінгіштігі ұғымымен тығыз байланысты. Бұл ұғым бізге әсіресе берілген
сандардың бірі екіншісіне бөлінетін-бөлінбейтінін және де қандай қалдық
қалатынын білу керек болғанда аса қажет болмақ.
Алгебра және сандар теориясын оқу барысында мектеп матемтикасымен
тығыз байланысты көптеген тақырыптар қарастырылады. Арифметикадағы қосу,
алу, көбейту, бөлу амалдары математикалық объектілер жиынындағы алгебралық
операциялар болып жалпыланады. Арифметикадағы қалдықты бөлу, сандардың
бөлінгіштігі, үлкен,кіші, тағы басқа ұғымдар, геометриядағы фигуралардың
ұқсастығы, түзулердің параллельдігі, перпендикуляр болуы,тағы басқа ұғымдар
бинарлық қатынастың дербес жағдай екендігі көрсетіледі. Нөлдің қасиеті,
таңбалар ережесі 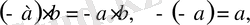минуспен байланысты амалдардың басқа қасиеттері
мектеп математикасында дәлелдеусіз беріледі. Топтар, сақина, өріс
тақырыптары үйрену кезінде бұл қасиетердің барлығы және жақша ашу ережелері
дәлелдеумен беріледі.

1 САЛЫСТЫРУЛАР ТЕОРИЯСЫНЫҢ НЕГІЗІ
1.1 Салыстырулар және бірінші дәрежелі салыстырулардың қасиеттері

Сандардың элементар теориясының маңызды мәселедерінің бірі болып
табылатын салыстырулар теориясының негізіне тоқталайық. Салыстыру жөніндегі
ұғым, мұны ең алғаш рет қолданған Гаусс, бір санның екінші санға
бөлінгіштігі ұғымымен тығыз байланысты. Бұл ұғым бізге әсіресе берілген
сандардың бірі екіншісіне бөлінетін-бөлінбейтінің және де қандай қалдық
қалатынын білу керек болғанда аса қажет болмақ.
Мысалы, 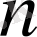-натурал сан болғанда, 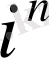мәнін табу үшін біз дәреже
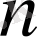-ді әдетте -ке бөлеміз де, тек қалдыққа ғана назар аударамыз.
Егер де
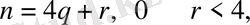болса,
онда болады.
Ал енді 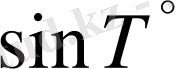мәнін табу керек болғанда да -тың 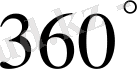-қаеселігін
ескермей, тек қалдықты ғана алмыз.
Бұл сияқты есептерді шешкенде салыстырулар теориясының көптеген
жеңілдік туғызатынын байқаймыз.
Айталық -алдын ала белгіленген бүтін оң сан делік.Былайғы жерде
мұны біз салыстыру модулы деп атайтын боламыз. Егер 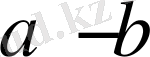(не )
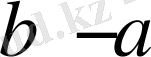айырмасы 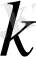санына бөлінетін болса, онда бүтін мен 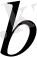екі сан
модулы бойынша өзара салыстырымды делінеді .
Гаусс қолданған белгілеу бойынша саны 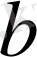санымен
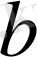салыстырымды. мен сандары салыстыру мүшелері деп аталады.
Мысалы, мен сандары 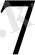модулы бойынша өз ара салыстырымды：

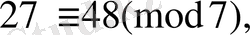
өйткені 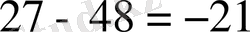саны 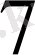-ге бөлінеді. Алайда 37мен 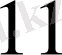сандары 7
модулы бойынша өз ара салыстырымды емес

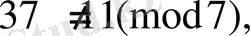
өйткені 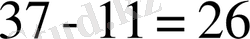саны 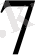-ге бөлінбейді.
Анықтама 1. және 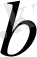бүтін сандарын санына бөлгенде
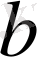қалдықтары тең болса, онда және сандарын модулы бойынша
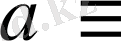
салыстырымды (немесе тең қалдықты) дейді және деп жазады.
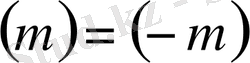болғаның есептейміз.

Егер 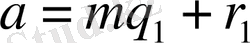, 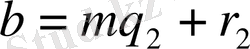және болса, онда
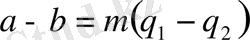
демек .

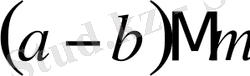1 Қасиет. Салыстырымдылық қатынасы рефлексифті, симметриялы,
транзитивті, яғни - эквиваленттілік қатынас.
а) 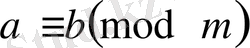-рефлексифті Кез келген сан өзімен өзі салыстырымды.
Шынындада мен 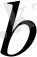айырмасы қашанда -ге бөлінеді.
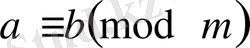
б) 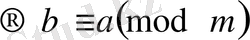-симметриялы. Шынындада 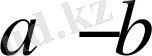мен 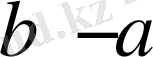айырмасы қашанда
санына бөлінеді
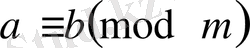
в) 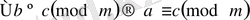-транзитивтік
2 Қасиет. Егер 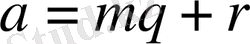, онда
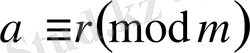
Дербес жағдай, егер болса, онда
3 Қасиет. Екі салыстыруды мүшелеп қосуғада, алуға да болады;
яғни

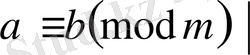
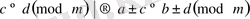
4 Қасиет. 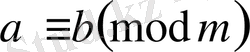болса, онда

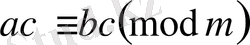
5 Қасиет. Екі салыстыруды мүшелеп көбейтуге болады, яғни

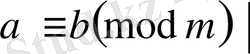
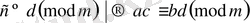
Салдар. Егер 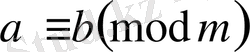болса, онда . Басқаша айтқанда, салыстырудың
екі жақ бөлігін де бірдей дәрежеге шығаруға болады.

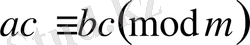6 Қасиет. Егер және 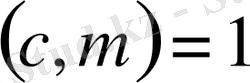болса, онда
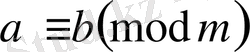
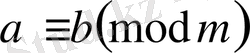7 Қасиет. Егер және 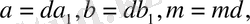онда .
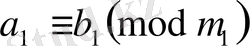Яғни салыстырудың екі жағын және модульді олардың ортақ бөлінгішіне
қысқартуға болады.
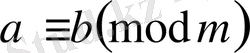8 Қасиет. Егер және 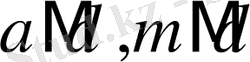болса, онда 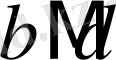болады.
Яғни
салыстырудың бір жағы және12 модуль бір 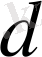санына бөлінсе, онда
салыстырудың екінші жағы да осы 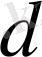саныны бөлінеді.
9 Қасиет. 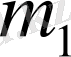саны модулының бөлгіші болсын. Егер
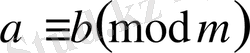болса,
онда .
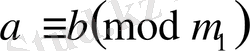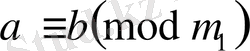
10 Қасиеті. Егер 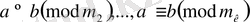, , онда
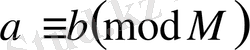, бұндағы М=ЕКОЕ .
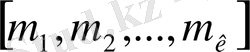10 қасиеттің бірнеше маңызды қолданулары бар. Соның бірі ретінде
3-ке
бөлінгіштік белгілерін келтірейік.
Кез келген N натурал саның мына түрдегі жүйелі сан ретінде жазуға
болады.

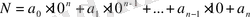. Енді

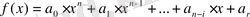көпмүшені қарастырайық.

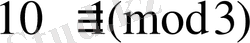
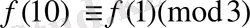немесе

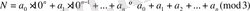
Сандар класы. Толық және келтірілген қалындылар системасы.
Барлық бүтін сандар жиынын k модулі бойынша, мынадай принципке сүйене
отырып, сандар класына бөлеміз: k санына бөлгенде бірдей қалдық шығатын
барлық бүтін сандарды бғана класқа жатқызамыз.
Қандай бүтін сан болса да, оны k ға бөлгенде бір ғана қалдық шығады,
сондықтан әрбір бүтін сан тек бір ғана классқа енеді. k санына бөлгенде
шығатын қалдықтар мынадай: 0,1,2,... k -1; сондықтан k модулі бойынша
сандардың мынадай К кластары табылады:
1 К 0 класына k-ға бүтіндей бөлінетін барлық бүтін сандар және 0и
саны енеді. Ендеше К 0 мына сандардан құралады[20,21,22]:

0, k, 2k, 3k, ... .

2 К 1 класына k –ға бөлгенде 1 қалдық шығатын барлық бүтін сандар
және 1 саны енеді. Ендеше К 1 класы мына сандардан құралады :

1, k+1, 2k+1, 3k+1, ...

3 К 2 класы мына салдарлардан құралады:

2, k+2, 2k+2, 3k+2, ...
Бұлардың әрқайсысын да k-ға бөлгенде 2 шығып отырады.
Ақырында, соңғы К k-1 класына мына сандар енеді:

k-1, 2k-1, 3k-1, ...

бұларды k –ға бөлгенде шығатын қалдық k-1-ге тең.
Сандар класының анықтамасына қарағанда бір ғана кластың сандары k
модулі бойынша өз ара салыстырымды екені, ал әр түрлі кластардың сандары
салыстырымды емес екені түсінікті.
Егер де а0-К0 класының кез келген саны, ал а1-К1 класының, а2-К2
класының, ... аk-1-Кk-1 класының саны болса, онда мына салыстырулардың
орындалатындығы түсінікті.

а0 ≡0(mod k)
a1≡1(mod k)
a2≡2(mod k)
... ... ... ... ... ... ..
ak-1≡k-1(mod k)

Kµ класыныңи кез келген саны мына түрде жазылады: kq+µ, мұнда
0≤µk. q-кез келген бүтін сан.
Бір ғана кластың сандары жөнінде мына теорема дұрыс болмақ.
Теорема. Егер а саны Kµ класының кез келген саны болса, онда осы
кластың барлық санары а мен k –ның ортақ бөлгіштерінің қай-қайсысына да
бөлінеді.
Шынында да, егер а´- Kµ класының кез келген саны болса, онда сандар
класының анықтамасы бойынша
а´≡а(mod k) болады, яғни а´=a+kt, мұнда t-бүтін сан
Бұған қарағанда, егер а мен k сандарының ортақ бөлінгіші σ болса,онда
бұл σ саны а´ санының да бөлгіші болмақ. Дербес жағдайда а мен k сандарының
ең үлкен ортақ бөлгіші а´санының да бөлгіші болмақ , сондықтан а мен k
сандарының ең үлкен ортақ бөлгіші а´ пен k сандарының ең үлкен ортақ
бөлгіші мен бірдей болады.

(а, k)=(а´, k)

Сонымен, бір кластың барлық сандарының модулі мен ортақ бөлгіштері
бірдей болады. Осымен теорема толық дәлелденді.
Қорытындыда мынадай бір маңызды ескертпе келтіреміз: модульдары k´
мен k, k´=km сандары кластарының арасындағы байланыс жөнінде. Модулі k´
әрбір клас модулі k болатын т кластарға ажырай алатындығын түсіну оңай.
Шынында да модулі k´ қалындылардың толық системасы мына сандар болмақ : 0,
1, 2, ... k´-1 бұларды таблицаға былай жазуға болады.

0 1 2 ... .. k-1
k k +1 k +2 ... 2 k-1
2k 2 k+1 2 k+2 ... 3 k-1
... ... ... ... ...
(т-1) k (т-1) k+1 (т-1) k+2 ... . т k-1

Бұл таблицаның бірінші бағанындағы барлық сандардың k модулі бойынша
өз ара салыстырымдылығы түсінікті, бұлай болса, бұл сандардың барлығы да
модулі k болатын бір ғана класқа енед. Таблицаның қалған бағандарының
әрқайсысындағы сандар жөнінде де осыны айтуға болады.
Таблицаның жоғарғы, бірінші жолындағы сандар модулі k
қалындыларының толық системасы болып табылады, ал қалған жолдардағы сандар
сол бірінші жол сандарына ретімен k, 2 k, ... , (т-1) k сандарын қосқанда
шығып отырады. Ендеше, біз жасаған ұйғарым дәлелденді.
Модулі k=2 кластардың ажырау процесін схема түрінде былай
көрсетуге болады. (k´=6 десек)

k=2

k=6

Ал k және k´, k´ =km модульдері үшін схема мынадай

k

k´

Айталық (mod k) бойынша барлық кластар K0, K1 , ... ...Kk-1 болсын.
Әрбір класс сол кластың кез келген кілі арқылы бір мәнді анықталады. Әрбір
кластан бір-бір өкіл белгілеп алайық : r0 , r1, r2, rk-1 Кі(і=0,
1, 2, ...k-1.) жатады r1, Сандар кластарын өз ара қосуға, азайтуға және
көбейтуге болады.

Эйлер мен Ферма теоремалары

Теорема (Эйлер теоремасы) Модуль т мен өз ара жай кез келген а саны
үшін мын салыстыру
Егер және өзара жай сандар болса, онда

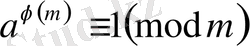(5)

Дәлелдеу. Егер 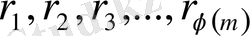-оң ең кіші модулы бойынша қалындылардың
келтірілген системасы болса, онда
Шарт бойынша 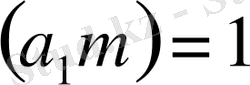болған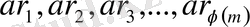да бұнда модулы бойынша
қалындылардың келтірілген системасы. Яғни өзара салыстырымсыз
бойынша және әр қалындылар класында
жатады. Бұл сандарды оң кіші қалдықтармен алмастырайық.

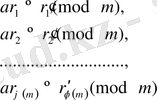(6)

Оң кіші қалдықтар 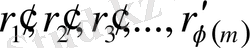қалындықтары да 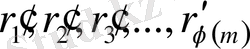қалдықтары сияқты ,
модулы қалындылардың келтірілген системасын құрайды, тек айырмашылығы
орналасу тәртібінде ғана. Сондықтан,
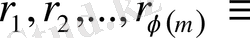
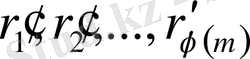және бұл көбейтінді модуль мен өзара жай. (6)
салыстыруларын мүшелеп көбейтейік. Сонда

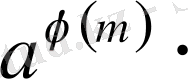
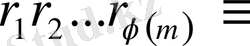
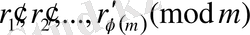
Бұл салыстыруды 6 қасиет бойынша қысқартсақ

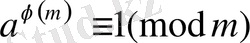шығады

Ферма теоремасы

Жай P санына бөлінбейтін кез келген 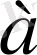саны үшін әрқашанда мына
салыстыру

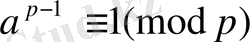(7)
Орындалады.
Бұл теорема болғанда Эйлер теоремасынан шығады.
Ферма формуласы. Жай р санына бөлінбейтін кез келген а саны үшін
әрқашанда мына салыстыру

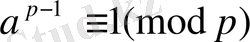
орындалады.
Ферма формуласын былай да жазуға болады:

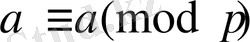
Ал бұл формула кез келген а саны үшін а бүтін саны үшін дұрыс.
Мысал. Егер k=48 болса, онда φ(48)=16 a болғанда
5161(mod48) шығады
Тағы да мынадай мысал келтіруге болады.
(3201-2302+1) саны жай р=101 санына бөлінеді.
Ферма формуласы бойынша жай р=101 саны үшін былай болады:

31001(mod 101)
21001(mod 101)

Алдыңғы салыстырудың екі жақ бөлігін де екінші дәрежеге, ал екінші
салыстыруды үшінші дәрежеге шығарып, мынаны табамыз:

32001(mod 101) 23001(mod 101)
не
32013(mod 101) 23024(mod 101)

Соңғы екі салыстырудың алдыңғысынан соңғысын мүшелеп шегеріп, барлық
мүшелерді бір жаққа шығарсақ, мынау шығады:

3201-2302+10(mod 101)

олай болса, (3201-2302+1) саны 101 ге бөлінеді.
Салдар. Егер p жай сан болса, онда кез келген үшін
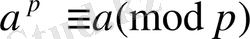
салыстыруы орындалады. Дәлелдеу үшін (7) екі жағын көбейтсек
болды.
Ескерту. Эйлер және Ферма теоремалары сандар теориясының әртүрлі
мәселелерінде қолданылады. Мысалы, бөлгендегі қалдықты табу үшін, 1-
ші
дәрежелі салыстыруды шешу үшін, шексіз ондық бөлшектің период
ұзындығын
табу үшін, тағы басқада жерлерде.

1.2 Жоғары дәрежелі салыстырулар

Енді біз жоғары дәрежелі мынадай

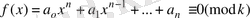(8)

салыстырулардың аса қажетті қасиеттерін қарастыруға көшеміз, мұның
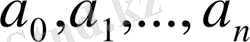коэффициенттері- бүтін сандар.
(8) салыстыру, тек егер 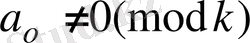болса, -дәрежелі салыстыру деп
аталатыны белгілі. Салыстыру дәрежесі, жалпы алғанда,полином дәрежесіне тен
бола бермейтіні мына мысалдан-ақ көреміз. 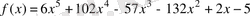полиномының дәрежесі 5-ке
тең де, ал 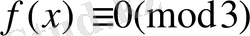салыстыруының дәрежесі бірінші дәрежеге ғана.
Олай болса, салыстырудың дәрежесін анықтағанда, аса мұқият болған
жөн: салыстырудың дәрежесін анықтамай тұрып, алдымен осы тараудың өткен
параграфтарында айтылған мүмкін ықшамдаулардың барлығын орындап алу керек,
(8) салыстырудың шешімі деп полиномын модулы мен еселік санға
айналдыратын кез келген бүтін санды, олай болса сол санмен анықталатын
сандар класын айтады. Салыстыруды шешеш келе, салыстырудың барлық
салыстырымды емес түбірлерін табамыз, бұл түбірлер әдетте ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.