Функция ұғымы

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Жоспар:

Кіріспе

Функция ұғымының пайда болу тарихы

Негізгі бөлім

Функцияларды теңсіздіктер немесе теңдеулер шешуде қолдану

Кіріспе

Функция ұғымының даму тарихы.

Функция - математикалық және жалпығылыми ұғымдардың негізгі бөлігі болып табылады. Шын әлемді танып білуде функция маңызды рөлге ие болды және қазіргі уақытта да ие.

Функционалдық тәуелділік идеясы ежелден-ақ басталған. Оның құрылымы ең алғаш математикалық анықталған шамаарлас қатынастарда, сандармен іс-әрекеттің алғаш ережелерінде және белгілі бір фигуралардың ауданын, көлемін табуға арналған формулаларында көрінеді. Осылай, вавилон (4-5 мың жыл бұрын) ғалымдары, дұрыс білмей отырып, шеңбер ауданы оның радиусынан басталған функция деп анықтаған. Оны анықтаудың дөрекі формуласы формуласы болса да (S=3r ² ), ол кезде жаңалық үлкен мәнге ие болды. Функцияны кестелік құрудың мысалдарына вавилондықтардың, ежелгі гректердің, үндістердің астрономиялық кестелері, ал функцияның сөзбен берілуіне диаметеріндегі шеңбер және шаршы аудандарының қатынасының тұрақтылығы туралы теоремасын немесе коникалық қималардың антикалық анықтамаларын (осы қисықтар геометриялық кейпінде қарастырылды) мысал етіп қарастыра аламыз.

Тек 17 ғасырдан бастап, математика ғылымына айнымалылардың еңгізілуімен функция ұғымы түгелімен өзгеріп, көп қолданыла бастайды.

17 ғасырда функция ұғымының пайда болуына жолды француз ғалымдары Франсуа Виет және Рене Декарт ашты, олар кейін жалпы әлем мойындаған біріңғай математикалық белгілеуді құрастырды. Біріңғай белгілеу ұсынылды: белгісіздерді - латын алфавитінің соңғы әріптерімен - x, y, z; белгілілерді алғашқы әріптермен - a, b, c, . . . және т. с. . Әрбір әріп арқылы тек нақты мәліметтерді ғана емес, басқа да мәліметтерді түсінуге болтын еді. Осылай, математика ғылымына өзгерту идеясы келді. Нәтижесінде, жалпы формулалар құрастыруға мүмкіндік туды.

Сонымен қатар, Декарт пен Фермде (1601-1665) геометриялық еңбектерінде айнымалы шама және тік бұрышты координаталар жүйесі туралы анық түсінік береді. 1637 жылғы «Геометрия» еңбегінде Декарт функция ұғымына түсінік береді, нүкте ординатасының өзгерісін абцисса өзгеруіне тәуелділігін зерттеді. Бірақ, ол тек теңдеулер арқылы көрсетуге болатын ғана және көбінесе алгебралық қисықтарды қарастырды. Кейін функция ұғымы анықтала бастады. 1671 жылы Ньютон функцияны айнымалы шама деп есептеді, ол уақыт өткен сайын өзгереді деп ойлаған. («флюента» деп атаған) .

В “Геометрии” Декарта и работах Ферма, Ньютона и Лейбница понятие функции носило по существу интуитивный характер и было связано либо с геометрическими, либо с механическими представлениями: ординаты точек кривых - функция от абсцисс (x) ; путь и скорость - функция от времени (t) и т. п.

Негізгі бөлім

Теңдеулерді шешуде функцияны қолдану

Теңдеулерді шешуде графиктерді қолдану.

I) Квадрат теңдеуді графикалық әдіспен шешу:

Берілген квадрат теңдеуді қарастырайық: x ² +px+q=0;

Оны осылай өзгертеміз: x ² =-px-q. (1)

Тәуелділіктер графиктерін құрамыз: y=x ² и y=-px-q.

Бірінші тәуелділік графигі бізге белгісіз, ол парабола болады; екінші тәуелділік - сызықтық; оның графигі түзу сызық болып табылады. (1) теңдеу бойынша х оның шешімі болып шықса, екі графиктің де координаталардың нүктелері өзара тең болады. Осылай, берілген х мағынасына параболадағы бір ғана нүкте сәйкес келеді, түзуде де осылай, яғни парабола мен түзу абциссасы х нүктесінде қиылысады.

Нәтижесінде, квадрат теңдеуді шешудің келесі графикалық әдісі шығады: у=х ² параболасын, нүктелер арқылы у=-рх-q түзуін сызамыз.

Егер түзу мен парабола қиылысса, онда қиылысу нүктелерінің абциссалары квадрат теңдеудің түбірлепі болады. Осы әдісін аса нақты шешім қажет емес болса өте ыңғайлы.

Мысалдар:

1. 4x ² -12x+7=0 теңдігін шешейік.

Оны осы түрде береміз: x ² =3x-7/4.

y=x ² параболасын және y=3x-7/4 түзуін құрамыз.

1 сурет.

Түзу құру үшін, мысалға мына нүктелерді алуға болады:

(0; -7/4) және (2; 17/4) . Парабола және түзу абциссамен екі нүктеде қиылысады: x ₁ =0. 8 и x ₂ =2. 2 (1 суретті қараңыз) .

2 Мысал: x ² -x+1=0 теңдігін шешейік.

Теңдеуді осы түрде жазсақ: x ² =x-1.

у=х ² параболасын у=х-1 түзуін құрсақ, олардың қиылыспайтындығын көреміз (2-сурет) . Сондықтан, теңдеудің түбірі жоқ деп айта аламыз.

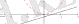
2-сурет

Оны тексерейік. Дискриминантын есептесейік:

D=(-1) 2-4=-3<0,

Сондықтан, теңдеудің түбірі болмайды.

3. Теңдеуді шешейік: x ² -2x+1=0

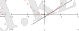3-сурет.

Егер, осы у=х ² параболасын және у=2х-1 түзіуін ыңғайлап салсақ, олардың біріңғай нүктесі бар екендігін (3-суретте түзу параболаны жанайды) көреміз - х=1, у=1; сондықтан теңдеудің бір ғана түбірі болады. (осыны есептеулер арқылы міндеттір түрде тексереміз) .

II) Теңдеулер жүйесі.

Екі айнымалысы бар теңдеудің графигі деп координаталар жүйесінің бірнеше нүктелерін атаймыз, олардың координаталары теңдеуді дұрыс теңдікке айналдырады. Екі айнымалысы бар графиктері әр түрлі болып келеді. Мысалы, 2х+3у=15 теңдеуінің графигі түзу болады, ал у=0. 5х ² -2 теңдігінікі -парабола, х ² +у ² =4 - шеңбер, және т. с. с. .

Екі айнымалысы бар бүтін теңдеудің дәрежесі бір айнымалысы бар бүтін теңдеудің дәржесі секілді анықталады. Егер екі айнымалысы бар теңдеудің сол жағы стандартты түрдегі көпмүше болып берілсе, ал оң жағы 0 саны болса, онда теңдеу дәрежесі көпмүшенің дәрежесіне тең болады. Қандай-да болсын екі айнымалысы бар теңдеудің дәрежесін анықтау үшін, оны соған тең теңдеумен алмастырады. Сонда, оның сол жағы - стандартты түрдегі көпмүше, ал оң жағы нөл болады. Шешудің графикалық жолын қарастырайық.

Мысал 1: жүйені шеш ⌠ x ² +y ² =25 (1)

⌠y=-x ² +2x+5 (2)

Бір координаталар жүйесінде теңдеулер графиктерін құрамыз (4 сурет)

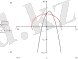
х ² +у ² =25 және у=-х ² +2х+5 графиктерін бір координата жүйесінде салдық.

Шеңбердің қандай-да болсын нүктесінің координатасы (1) теңдеудің шешімі болады, ал параболаның қандай-да болсын координаталары (2) теңдеудің шешімі болады. Осыдан, шеңбер мен параболаның қиылысу нүктелері бірінші теңдеудің де, екіншісінің де түбірі болады, яғни қарастырылып жатқан жүйенің шешімі болады. Суретті қолдана отырып, координата нүктелерінің маңайындағы жақын түбірлерін табамыз: А(-2, 2; -4, 5), В(0; 5), С(2, 2; 4, 5), D(4; -3) . Нәтижесінде, теңдеулер жүйесінің төрт шешімі бар екендігіне келеміз:

х1≈-2, 2, у1≈-4, 5; х2≈0, у2≈5;

х3≈2, 2, у3≈4, 5; х4≈4, у4≈-3.

Табылған шешімдерді теңдеулер жүйесіне қойсақ, осы шешімдердің екіншісі және төртіншісі - нақты, ал біріншсі мен үшіншісі - жақын мәндер екендігін көре аламыз.

III) Тригонометриялық теңдеулер:

Тригогнометриялық теңдеулерді анализдеу немесе графикалық жолмен шеше аламыз. Графикалық жолмен шешу әдісін мына мысалда қарастырамыз.

5-сурет.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.