Қатты денелердің жылу өткізгіштігі мен катты денелердің молекула-кинетикалық теориясының негізгі ұғымдары ондағы тасымалдау процестері, соның ішінде стационар және стационар емес жағдайлардағы жылу өткізгіштік процесі

Пән: Физика
Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 54 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе

1. Қатты денелердің жылу өткізгіштігі (стационар жағдай ) .

1. 1 Қатты денелердің молекула - кинетикалық теориясының негізгі

ұғымдары мен түсініктері.

1. 2 Қатты денелердегі стационарлық жағдайдағы тасымалдау

процестері.

1. 3 Жылу өткізгіштік.

1. 4 Жылу өткізгіштік коэффицентін анықтау әдістері.

2. Тәжірибелік жұмыстардың тәсілдері

2. 1 Қатты денлердің жылу өткізгіштік қасиеттерінің зерттеу әдістері .

2. 3 Тәжірибелік тәсілдер және зерттеу нәтижелерін талдау .

Зерттеу объектісі, тәжірбиелік қондырғы және зерттеу жұмыстарының

әдістері.

3 SiO , Al O тотықтарының жылу өткізгіштігінің температураға

тәуелділігі. .

3. 1 SiO , Al O жылу өткізгіштік қасиеттері .

3. 2 Полифазалық керамикалық үлгінің жылу өткізгішінің температураға

тәуелді өзгеруі.

Қорытынды.

Пайдаланылған әдебиеттер.

Кіріспе

Бұл дипломдық жұмыста жалпы қатты денелердің жылу өткізгіштігі мен катты денелердің молекула-кинетикалық теориясының негізгі ұғымдары ондағы тасымалдау процестері, соның ішінде стационар және стационар емес жағдайлардағы жылу өткізгіштік процесі қарастырылады. Қатты денеде жылуды тасымалдау механизмі тек жылу өткізгіштік арқылы жүзеге асырылады.

Жалпы жұмысымның мақсаты - жаңа керамикалық материалдардың жылу өткізгіштік коэффицентінің температураға тәуелділігін анықтау болып табылады. Сондықтан зерттеу нысаны ретінде жаңа керамикалық материалдарды алдық .

Соңғы жылдары біздің планетамызда адамзаттың жан -жақты жүргізіп жатқан белсенді қызыметтерінің нәтижесінде үлкенді- кішілі экологиялық апаттар орын алуда . . .

Бүгінгі таңда жедел дамып отырған ғылыми техникалық прогрестің нәтижесінде пайда болған осындай үлкен экологиялық проблемалар кездейсоқ пайда болған жоқ.

Экология, технология және өндіріс . . . бұл түсініктердің арасында тығыз байланыс жатыр. Жыл сайын елімізде көмір, химия, энергетика, металлургия және тағы басқа өнеркәсіптермен миллиондаған тонна қалдықтар бөлінуде . Бүгінгі экологиялық проблемалардың бір тамыры міне осындай өнеркәсіп қалдықтарының зиянды әсерлерінен арылу мәселесіне келіп тіреледі.

Сонымен экологиялық проблемаларда шешудің белгілі бір бағыты өнеркәсіп қалдықтарын халық шаруашылығының қажетіне жаратудың жан-жақты әдістерін таба отырып, «қалдықсыз», «қалдығы аз » сияқты озықты үнемді технологияларды ойлап табу жұмыстарымен тікелей байланысты.

Халық шаруашылығының сан алуан салаларының ішінде әсіресе көмір өнеркәсібінен жыл сайын бөлінетін «қалдықтардың» қоры өте мол. Мысалы: көмірді жерден қазып алу, сонан соң оны арнайы фабрикаларда байыту, дайын болған көмірді жерден қазып алу үшін жағу жолдарының әрқайсысында белгілі бір қалдықтар бөлініп отырады. Осындай қалдықтардың бірі жылу электр станцияларында майда көмір тозаңын жағудан қалатын күл болып табылады. Жағу барысында әр тонна көмірден 30-50 процент шамасында күл бөлініп шығатынын ескерсек, қорының орасан зор екендігі өзінен-өзі түсінікті. Міне, сонықтанда осы жүздеген миллион тонна күлді зиянды қалдықтан кәделі материалдарға айналдыру, яғни тиімді шикізат есебінде пайдалану мәселелері бұл күндері үлкен әлеуметтік проблемаға айналды.

Бұл проблеманың шешілуі әсіресе Екібастұз, Қарағанды сияқты үлкен көмір бассейндері бар. Қазақстан үшін өте маңызды. Қазіргі таңда күл қалдықтарын халық шаруашылығында пайдалану мәселелерін қарастыру жолында біздің еліміздің, сондай-ақ шет елдердің бір қатар ғылыми орталықтарында нәтижелі жұмыстар жүргізілуде. Бұл жұмыстардың барысы күл қалдықтарын сан-алуан құрылыс материалдарын жасауда қосымша шикізат есебінде пайдалануға мүмкіндіктер мол екендігін көрсетті.

1. Қатты денелердің жылу өткізгіштігі (стационарлық жағдай)

. Қатты денелердің молекула - кинетикалық теориясының негізгі

ұғымдары мен түсініктері.

Біз қатты дене - жер шарының бетінде қатты денелерден салынған құрылыстарда, үйлерде өмір сүріп жатырмыз. Біздің денеміздің құрамында шамамен 65% су болғанның өзінде (мида 80%) ол қатты денеге жатады. Еңбек құралдары, машиналар да қатты денелерден жасалған. Қатты денелердің қасиеттерін білу тіршілік үшін қажет.

Қатты денелер сұйықтар сияқты өзінің көлемін ғана сақтап қоймайды, сонымен бірге пішінін де сақтайды. Олар негізінен кристалл күйде болады екен.

Қатты денелердің атомдары немесе молекулалары, сұйықтардікіне қарағанда, белгілі бір тепе - теңдік қалыптың маңында тербеліп тұрады. Кей кезде молекулалар өздерінің тепе - теңдік қалпын өзгертеді, бірақ бұл өте сирек болады. Сол себепті қатты денелер көлемін ғана емес, пішінін де сақтайды.

Қатты денелер өздерінің физикалық қасиеттері жағынан бірінен - бірінің өте үлкен айырмашылықтары бар екі топқа, атап айтқанда: 1) кристалл денелер және 2) аморф денелер болып бөлінеді.

Аморфтық денелердің физикалық қасиеттері барлық бағыттар бойынша бірдей болады. Аморфтық денелерге шыны, пластмассалар және т. б. жатады. Аморфтық денелер физикалық қасиеттерінің изотроптылығы оларды құрайтын атомдар мен молекулалардың ретсіз орналасуымен түсіндіріледі.

Атомдары мен молекулалары реттелген, периодты қайталанылатын ішкі құрылымды түзе орналасатын қатты денелер кристалдар деп аталады. Кристалдық денелердің қасиеттері әртүрлі бағыттарда бірдей емес.

Кристалдардың бұл қасиетін анизатроптық деп атайды. Мысалы, кристалл дененің жылулық ұлғаю коэффиценті әр түрлі бағытта түрліше болады; кристалдардың механикалық, оптикалық және электрлік қасиеттері әр түрлі бағытта бірдей болмайды. Кристалдың өзіне тән сыртқы белгісі - оның геометриялық формасының дұрыс болатындығы. Терезе шынысының бетіне су қатқанда байқалатын мұз кристалдарының геометриялық дұрыс формалары жалпыға белгілі. Кристалдардың жан - жағы айнадай жазық болып келеді, ол жазық жақтар бірімен - бірі түзу қырлар және үшкір бұрыштар жасап қиылысады. Әдетте жақтар біріне қарағанда бірі симметриялы болып орналасады.

Кристалдың жазықтары белгілі бір бағытта орналасады, сындырғанда олар көбінесе осы жазықтардың бойымен жарылады. Мысалы, тас тұзының кристалдары ұрғанда өз ара перпендикуляр жазықтықтардың бойымен жарылып сынады, сонда тас тұзының кесектері параллелипипед формалы болады. Ал аморф денелердің сынған жерлері ойлы - қырлы болады; жарылып сынған шыны ұсақтарының белгілі бір формасы болмайды.

Кристалл денелер монокристалдар және поликристалдар болып екіге бөлінеді. Монокристалдың басты ерекшелігі оның бүкіл көлемінде ішкі құрылымының периодты қайталануы болып табылады. Поликристалл бейберекет орналасқан кіші кристалдар жиынтығынан тұрады. Табиғатта кездесетін қатты денелердің басым көпшілігі - тас, құм, металдар, тұздар және т. б. поликристалдар болып табылады. Поликристалл дененің әрбір кіші монокристалы анизотропты, ал поликристал дене изотропты. Кристалдарды құрайтын бөлшектердің кеңістікте дұрыс кристалдық тор түзетіндігі - тәжірибеде анықталған. Кристалдық тор деп түйіндерінде кристалды құрайтын бөлшектер орналасатын кеңістіктік торды айтады. Кристалдар табандарында тек дұрыс үшбұрыш, квадрат, параллелограм және алтыбұрыш жататын әр түрлі призмалар мен пирамиданың пішінінде болады.

Кристалдағы бөлшектердің периодты қайталанып орналасуын кристалл торы белгілі симметрияға ие екен дейді. Фигураның пішінінің қандай да бір дұрыстығын сипаттайтын қасиетін фигураның симметриясы дейді.

Кристалдардың симметриясын жалпы түрде Е. С. Федоров қарастырған. Ол бөлшектердің кристалдарда орналасуының 230 түрі бар екенін көрсетті. Арасындағы байланысты анықтай отырып, кристалдық - химиялық анализдің методын тағайындады.

Кристалдың физикалық типтері.

Кристал торының түйіндерінде атомдар, иондар, молекулалар болуы мүмкін. Түйіндерде орналасқан бөлшектердің арасында белгілі күштер әсер етеді. Кристалдық тордың түйіндеріндегі бөлшектердің табиғатына және олардың арасындағы өзара әрекет күштердің қасиеттеріне қарай кристалдар төрт типке ажыратылады: атомдық, иондық, металдық және молекулалық.

Атомдық кристалдар. Атомдық кристалл түйіндерінде электрлі бейтарап атомдар орналасады. Түйіндердегі атомдарды ұстап тұратын байланысты коваленттік деп атайды. Бұл байланыс тек қана атомдық кристалдарда емес, көптеген екі атомды қосындыларда кездеседі.

Иондық кристалдар. Иондық кристалдың түйіндерінде әр түрлі таңбалы иондар орналасады. Олардың арасындағы әсер күштері негізінен электрлік (Кулон күштері) болып келеді

Молекулалық кристалдар. Молекулалық кристалдардың түйіндерінде молекулалар орналасады. Түйіндердегі молекулаларды өзара молекулааралық күштер ұстап тұрады. Бұл күштер әлсіз, олар атомдардан молекула түзе алмайды. Молекулалық кристалдан тұратын заттар берік болмайды, олар тез буланып ұшып кетеді.

Металдық кристалдар. Металдық кристалдар торының ерекшелігі - металл атомдарынан оңай бөлініп шыққан сыртқы электрондар болады. Олар газ молекулалары сияқты ретсіз қозғалып, электронды газ түзеді. Сондықтан металл кристалын барлық түйіндерінде оң иондар орналасқан электронды газдың ішіндегі тор деп қарастыруға болады. Электронды газ арқасында металдар мынадай қасиеттерге ие болады: электр және жылу өткізгіштігі өте зор; жабысқақтығы, яғни пластиктігі бар; қақтауға төзімді немесе созымдылығы үлкен.

Қатты денелердің серпінділік қасиеттері.

Қатты дененің өлшемдері мен көлемінің және пішінінің өзгеруін деформация деп атайды. Деформациялар қатты денелерді қыздыру мен суыту кезінде және сыртқы күштердің әсерінен пайда болады. Деформация кезінде кристалл тордың түйіндерінде орналасқан бөлшектер өздерінің тепе - теңдік қалыптарынан ығыстырылады. Осының әсерінен деформацияланған қатты денеде серпінділік күші пайда болады.

Деформацияны туғызатын сыртқы күштердің әсері тоқталғаннан кейін денелердің өз өлшемдері мен пішінін және көлемін қалпына келтіру қасиеті серпінділік деп аталады. Дененің деформациясы кезінде пайда болатын және бөлшектердің ығысу бағытына қарсы бағытталған күшті Ғ серпінділік күші деп аталады.

Сыртқы күштердің әсері тоқталғаннан кейін жойылатын деформациялар серпінді деформациялар деп аталады.

Серпінді емес деформациялар сыртқы күштердің әсері тоқталғаннан кейін жойылмайды. Мұндай деформациялар пластикалық деформациялар деп аталады. Деформацияның ең қарапайым түрлері - созылу мен сығылу. Созылу мен сығылу деформациясы Е салыстырмалы созылумен сипатталады:

; (1. 1)

мұндағы 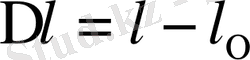- абсолют ұзару.

- мысалы, біліктің созылғанға дейінгі, ал 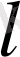- созылғаннан кейінгі ұзындықтары.

Серпінділік күш модулінің дене көлденең қимасының ауданына қатынасына тең шаманы 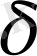механикалық кернеу деп атайды:

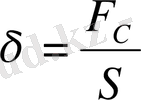; (1. 2)

Халықаралық бірліктер жүйесінде механикалық кернеу бірлігіне паскаль (Па) қабылданған: 1Па = 1 Н/м ² . Шамалы деформацияларда төмендегі қатынаспен анықталатын Гук заңы орындалады:

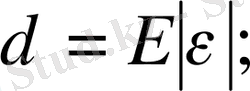
мұндағы Е пропорционалдық коэффициенті серпінділік модулі немесе Юнг модулі делінеді. Бір материалдан жасалған денелер үшін олардың өлшемдері мен пішініне байланыссыз серпінділік модулі бірдей:

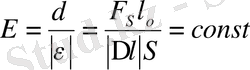(1. 3)

соңғы өрнектен

= (1. 4)

Біліктің К қаттылық коэффициенті: тең болады. Практикада қатты денелердің морттық деп аталатын қасиетінің маңызы зор. Егер материал болмашы деформацияларда қирап бүлінетін болса, ол материал морт деп саналады. Мысалы: шыны, фарфор және т. б.

Қатты денелердің жылулық ұлғаюы.

Тәжірибеге сәйкес температура жоғарылаған сайын қатты денелердің көлемі артатындығы белгілі. Қатты денеде берілген температурада молекулалар бір - бірінен белгілі қашықтықтарда орналасады да, тепе - теңдік қалыптардың маңында тербеліс жасап тұрады. Температураның жоғарылауымен тербеліс энергиясы артады. Басқаша сөзбен айтқанда, температура артқан сайын молекулалар бір - бірінен қашықтайды.

Абсолют нөлден алшақ тұрған температура аралығында көлемнің салыстырмалы өзгерісі температураның өзгерісіне пропорционал :

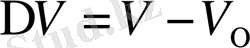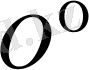
мұндағы β - көлемдік ұлғаю коэффициенті, яғни 1 Кельвинге келетін көлемнің салыстырмалы өзгерісі. , бұнда - = температураға сәйкес дененің көлемі және Т = t - t = t деп алсақ онда

V=V (1+βt),

Дененің тығыздығы үшін осыған ұқсас

(1+βt),

Көлемдік жылулық ұлғаю қатты денелер мен сұйықтарға бірдей қатыста болса, сызықтық жылулық ұлғаю тек қатты денелерге ғана тән.

Сызықтың жылулық ұлғаю берілген температуралық аралықта сызықтық ұлғаю коэффициентімен сипатталады:

(1+ ),

мұндағы l - дененің t = 0 температура кезіндегі ұзындығы, l - дененің t температурадағы ұзындығы шамасы 1 Kельвинге келетін ұзындықтың салыстырмалы өзгерісі.

Аз температура аралықтары үшін сызықтық және көлемдік ұлғаю коэффициенттерінің байланысы мына өрнекпен беріледі:

β ≈ 3 Equation. 3,

Қатты денелердің балқуы, кристалдану және сублимициясы.

Қатты денелердің сұйыққа айналуы балқу деп аталады. Балқу процесінде қатты дененің кристалл торы бұзылады. Балқу процесі кезінде қатты денеге берілетін барлық жылу мөлшері кристалдық торды бұзуға және сыртқы күштерге қарсы істелетін жұмысқа жұмсалады.

Балқу температурасында қатты дененің масса бірлігін сұйық күйге айналдыруға қажетті жылу мөлшерін λ меншікті балқу жылуы деп атайды.

Заттың сұйық күйден қатты кристалдық күйге өтуі кристалдану деп аталады. Кристалдану кезінде сұйық молекулаларының қозғалысы тәртіптеледі де, кристалдық тор түйіндерінің маңыңдағы жылулық тербеністерге ауысады. Сұйықтың масса бірлігі кристалданғанда меншікті балқу жылуына тең меншікті кристалдану жылуы бөлініп шығады.

Қатты денелердің булануын сублимиция деп атайды. Сублимиция кезінде молекулалар қатты дене бетінен тікелей “жұлқынып шығып” газ тәріздес күйге өтеді.

1. 2 Қатты денелердің стационарлық жағдайдағы тасымалдау процестері.

Егер қатты денелерде, қозғалмайтын сұйық пен газдарда температура әр түрлі нүктелерде бірдей болмаса, онда жылу өздігінен дененің температурасы жоғарырақ бөлігінен, температурасы төменірек бөлігіне ауысады. Мұндай үрдіс (процесс) жылу өткізгіштік деп аталады. Жылу өткізгіштік құбылысының ішкі механизмі молекула-кинетикалық теория тұрғысынан түсіндіріледі; берілген денедегі өте кішкентай бөлшектер (атом, электрон, молекула) арасындағы жылулық қозғалыс пен энергетикалық өзара әсерлесу салдарынан энергияның ауысуы жүзеге асырылады.

Жылу өткізгіштік процесі дене ішінде температураның таралуымен тығыз байланысты. Сондықтан да ең алдымен температура өрісі және температура градиенті ұғымын қалыптастыру қажет.

Температуралық өріс.

Температура, дененің жылулық күйі мен оның қызу дәрежесін анықтайтын көрсеткіші. Себебі, жылу өткізгіштік процесі кезінде дененің және бөліктерінің жылулық күйі әртүрлі, олай болса жалпы жағдайда τ уақыт және x, y, z координаттар функциясында температура t болады, яғни:

t = f (x, y, z) (1. 5)

Кеңістіктің барлық нүктесі үшін берілген уақыт моментіндегі температура мәндерінің жиынтығы температура өрісі деп аталады. (1. 5) теңдеуі осы өрістің математикалық теңдеуі болып табылады. Егер температура уақытқа байланысты өзгеретін болса, өріс бекітілмеген (стационар емес) деп, ал егер температура уақытқа байланысты өзгермейтін болса, өріс бекітілген (стационар) деп аталады.

Температура бір, екі және үш координаттың функциясы болуы мүмкін. Соған сәйкес бір, екі, үш өлшемді температуралық өріс деп аталады. Бір өлшемді стационарлық температура өрісінің теңдеуі қарапайым түрде былай өрнектеледі:

t= t (x) (1. 6)

Температураның градиенті.

Денеде кез - келген температура өрісінде әрқашан бірдей температурадағы нүктелер болады. Мұндай нүктелердің геометриялық орыны изотермиялық бетті кескіндейді. Өйткені, кеңістіктің бір нүктесінде және сол нүктеде бір уақытта екі әртүрлі температура болуы мүмкін емес, онда изотермиялық беттер бір - бірімен қиылыспайды, барлығы өзімен тұйықталады немесе дененің шекарасында аяқталып қалады. Демек, денедегі температураның өзгерісін оның тек бағытына қарап, изотермиялық беттердің қиылысуына қарап (1. 1 - сурет) бақылайды.

1. 1 - сурет. Температура градиентін анықтау

Сонымен, температураның кенет өзгеруімен изотермиялық бетке n нормаль бағыты туғызылады. температура өзгерісінің нормаль бойынша изотер-малар арасындағы қашықтыққа қатынасының шегін температураның градиенті деп атайды және былай белгіленеді:

lim 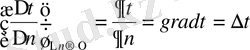; (1. 7)

Температуралық градиент температураның өсуіне қарай изотермиялық бетке нормаль бойынша бағытталған вектор болып табылады, өлшемі -

Жылу ағыны.

Жылу өздігінен температураның азайған жағына ауыса қояды. Уақыт бірлігінде қандай да бір бет арқылы ауысатын жылу мөлшерін Q жылу ағыны деп атайды. Беттің бірлігіне келетін жылу ағынын, жылу ағынының тығыздығы деп атайды, немесе меншікті жылу ағыны, немесе жылулық қысым деп аталады. Егер жылу ағыны изотермиялық беттің бірлігіне келетін болса, онда

q шамасы бағыты жылудың берілген нүктедегі таралу бағытымен сәйкес және температуралық градиент векторының бағытына қарама - қарсы вектор болып табылады. (1. 2 - сурет)

1. 2 - сурет. Фурье заңы.

4. Фурье заңы.

Қатты денелердің жылу өткізгіштік процесін зерттей отырып Фурье, берілген жылу мөлшері жылудың таралу бағытына перпендикуляр уақыт және көлденең қимасының ауданына, температураның төмендеуіне тәуелді екенін эксперимент жүзінде дәлелдеді (тағайындады) . Егер берілген жылу мөлшерін қима мен уақыт бірлігіне қатысты алсақ, онда белгіленген тәуелділік былай жазылады:

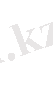
(1. 8)

(1. 8) теңдеуі - Фурье заңындағы жылу өткізгіштіктің негізгі заңының математикалық теңдеуі болып табылады. Бұл заң жылу өткізгіштіктің теориялық және эксперименттік зерттеулер процесінің негізіне жатады.

5. Жылу өткізгіштік коэфициенті.

(1. 8) теңдеуіндегі пропорционалдық көбейткіші жылу өткізгіштік коэффициенті деп аталады. Ол заттардың физикалық және олардың жылу өткізу қабілетін сипаттайды:

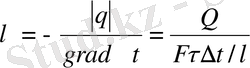(1. 9)

Жылу өткізгіштік коэффициентінің шамасы болып температураның өзгерісі кезінде изотермиялық беттің бір квадрат метрінен уақыт бірлігінде өтетін бірге тең жылу мөлшері саналады.

Әр түрлі заттар үшін жылу өткізгіштік коэффициенті әр түрлі және жалпы олардың құрылысына, тығыздығына, ылғалдылығына, қысымы мен температурасына байланысты. Бәрін бірге алғанда жылу өткізгіштік коэффициентінің шамасын дұрыс таңдау қатты қиындық туғызады. Сондықтан да жылу өткізгіштік коэффициентінің нақты шешімін тапқанда арнайы алдын - ала дайындалған материалды қолданады. Техникалық есептеуде жылу өткізгіштік шамасын анықтамалық таблицадан алынады. Сонан соң, алынған материалдың (құрылымы, тығыздығы, ылғалдығы, температурасы, қысымы) физикалық сипаттамаларының сәйкестігін қарастыру керек. Дененің әр бөлігінде жылу температурасының таралуы әр түрлі, сондықтан ең алдымен жылу өткізгіштік коэффициентінің температураға тәуелділігін білу керек. Үлкен санды материалдар үшін бұл тәуелділік түзу сызыққа жақын, демек:

, (1. 10)

мұндағы 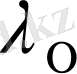- температурадағы жылу өткізгіштік коэффициенті; b -тәжірибеден алынған тұрақты.

а) газдың жылу өткізгіштік коэффициенті 0, 005-0, 5 Ва/(м ⁰ С) . аралығында жатады. Температураның жоғарлауымен 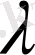өседі (сурет 1. 3), өте жоғарғы (200 бар көп) және төменгі (20 мм. сын. бағ аз) қысымдарды қоспағанда, қысымға тәуелді емес. 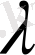үшін аддитивтік заңы қабылданбаған; сондықтан газ қоспалары үшін жылу өткізгіштік коэффициентін таблицалық мәліметтер жоқ кезде, тәжірибе жасау арқылы анықтайды.

б) Тамшылық сұйықтың жылу өткізгіштік коэффициенті 0. 08 - 0. 7 Вт/(м∙ ⁰ С) аралығында болады. Температуралық жоғарлауымен, сұйықтың біраз бөлігі үшін λ азаяды. (1. 4 - сурет), су мен глицеринді есепке алмағанда.

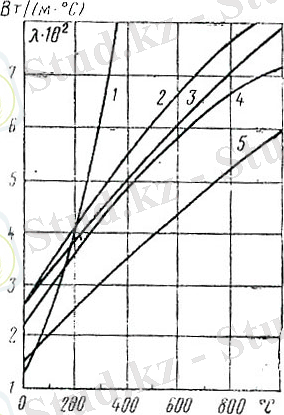
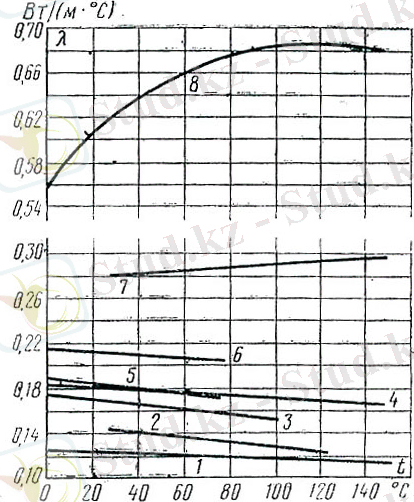
1. 3 - сурет. 1. 4 - сурет.

Кейбір газдардың 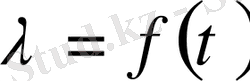Кейбір тамшылық сұйықтың

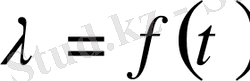
в) Құрылыс және жылу шығармайтын материалдардың жылу өткізгіштік коэффициенті 0. 02 - 3. 0 (м∙ ⁰ С) аралығында болады. Температураның жоғарлауымен өсіп отырады (1. 5 - сурет) . Ережедегідей тығыздығы үлкен материалдар үшін λ - шамасы жоғарғы мәнге ие. Ол да материалдың құрылымына, оның ылғалдылығына және кеуектігіне тәуелді. Құрғақ және суға қарағанда, ылғалды материалдар үшін жылу өткізгіштік коэффициенті әлде қайда жоғары болуы мүмкін. Мысалы, құрғақ кірпіш үшін λ=0. 03 , су үшін 0. 6, ал ылғалды кірпіш үшін 0. 9. Бұл жағдайда жылу өткізгіштің техникалық есебін шығарғанда, анықтағанда ерекше көңіл аудару керек. Жылу өткізгіштік коэффициенті төмен материалдар (0. 2 Вт/(м∙ ⁰ С) ден аз) жылу шығармау үшін қолданады және оны жылушығарғыш деп атайды.

г) металдардың жылу өткізгіштік коэффициенті 20 - 400 Вт/(м∙ ⁰ С) аралығында болады. Жылу өткізгіштігі ең жоғары металл - күміс (λ=410) , одан кейін таза мыс (λ=395) , алтын (λ=300) , алюминий (λ=210) және т. б. (1. 6 - сурет) . Температураның жоғарлауымен металдардың көпшілігі үшін жылу өткізгіштік коэффициенті азаяды. Әр түрлі қоспалардың тууымен байланысты дәл солай азаяды.

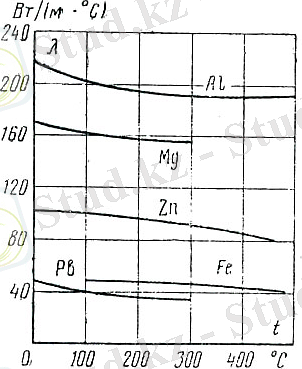
1. 5 - сурет. 1. 6 - сурет.

Кейбір жылу шығармайтын және Кейбір металдар үшін

отқа төзімді металдар үшін

Мысалы: таза мыс үшін λ=395 , сондай мыс үшін, бір - ақ мышьяк ізімен λ=142, 0, 1% көміртекті темір үшін λ=52, 1% көміртегі үшін λ=40 және 1, 5% көміртегі үшін λ=36. Шыныққан көміртекті болат үшін жылу өткізгіштік коэффициенті жұмсағына қарағанда 10 - 25% төмен, алайда қоспалардың әсері туралы жалпы заңдылықты бекіту мүмкін емес. Оның қорытпалары үшін тікелей тәжірибе жасау оның жылу өткізгіштік коэффициентінің шамасын анықтаудың бірден - бір әдісі болып табылады. Себебі, металдардың жылу өткізгіштігі сияқты негізінен еркін электрондардың диффузиясы арқылы анықталады, олай болса таза металдар үшін бұл шамалар бір - біріне перпендикуляр (Видеман - франц заңы) .

Төменде Фурье заңы негізінде стационарлық жүйедегі әр түрлі денелер үшін жылу өткізгіштік формуласын есептеп шығардық. Бұл формула қатты денелер үшін тек қатал түрде әділ болуы тиіс. Оны сұйықтар мен газдарға қолдану үшін конвекция және жылу шығару әсерін мүмкіндінше ескеру керек.