Болашақ математика мұғалімінің әдістемелік дайындығы: математикалық ұғымды қалыптастыру және оқытудағы анализ пен синтез


ЛЕКЦИЯЛАР
Болашақ математика мұғалімінің әдістемелік дайындығының жалпы мәселелері
Лекция 1
Математикалық ұғым және оны қалыптастыру
Біздің әрбір сөйлеміміздің сөзі белгілі бір заттардың тобын, класына жатып, оларды анықтайды, құбылыстардың өзара қатынасын бейнеледі. Егер сөз бізге бір затты басқа бір заттардан көптеген қасиеттерін ерекшелеп көрсетуге көмектессе, ойымызда ол зат ерекшеленіп елестесе не оларға тән ортақ қасиеттер мен байланыстарды көрсетілсе, онда ой заттың жалпы қасиеттерін бейнелей алады. Заттар арасындағы және құбылыстар мен қатынастардан, олардың нақты қасиеттерінен жалпылай қорытынды шығарылса, бұл олар туралы белгілі бір ұғым болады. Әрбір түсінік сөзбен бірге сәйкес түрленеді, сөз сөйлем туралы түсінікті елестетуге қызмет етеді.
- «Ұғым» термині әдетте біздің санамызда кейбір объектілері шындықтың қатынасы мен процестердің, кейбір заттар класының ойша бейнесін белгілеу үшін қолданылады. Математикалық ұғым біздің ойымызда белгілі формада нақты жағдайдан абстракцияланған шындықты бейнелейді.
Ұғым. Бір затты екінші заттан әр түрлі сапалары мен белгілеріне не ерекшеліктері арқылы ажыратылады. Әр түрлі объектілерден 1) жеке қасиеттері; 2) жалпы қасиеттерді бөліп аламыз.
- Бір айнымалыға тәуелді 2-дәрежелі теңдеу - квадрат теңдеу. Қазақстандағы ең ұзын өзен Іле -жеке қасиетке ие.
Адамдар - омыртқалылар класына жатады, сүт қоректі. Жалпы қасиеттің өзі дербес, тек бір топқа тән, жалпы қасиет бөлектенеді, егер заттың қасиеттерге, белгілерге, басқалардан бөлек қасиеттерге ие. Адамдар сөздері арқылы бөлінеді.
Объектілер қасиеттерінің адам миында ерекше бейнелену процесін - ұғым деп атайды. Ұғым біріншіден жоғары дәрежеде ұйымдасқан материяның жемісі; 2) ұғым материалды дүниені бейнелейді; 3) Ұғым - жалпылау, тану тәсілі ретінде қолданылады; 4) адам қызметінің өзгешелігін білдіреді; 5) адам санасына ұғымның қалыптасуы оның тікелей сөз, жазу не символ арқылы өрнектелуінен бөлінбейді. В. И. Лениннің анықтамасы бойынша «ұғым - материяның мидағы жоғарғы жемісі». Әрбір ұғым өзіне объектілер класын біріктіреді. (заттардың қатынасы) .
Ұғым мазмұннан және көлемнен тұрады. Ұғым көлемі - осы класқа жататын барлық объектілерді білдіреді., ұғым мазмұны объектілердің сипаттамалық қасиеті осы ұғымның мазмұны болады. Мысалы, «Үшбұрыш» ұғымы мүмкін болатын барлық үшбұрыштар класын білдіреді. (Бұл ұғымның көлемі) және сипаттамалық қасиет үш қабырғасы, үш төбесі, үшбұрышы (ұғымның мазмұны) ; «теңдеу» ұғымы - барлық мүмкін болатын теңдеулер класын біріктіреді (көлемі) және сипаттамалық қасиеті - бірнеше айнымалыдан тұратын теңдік (ұғымның мазмұны) ұғымның мазмұны анықтама арқылы, көлемі - классификациялау жолмен табылады.
- Ұғымды қалыптастыру- күрделі психологиялық процесс, білім берудің жай танымдық формасы - түйсіну. Әр кез келесі схема бойынша жүргізіледі.
Сезіну - қабылдау - түсінік - ұғым. Әдетте бұл процесс екі сатыдан тұрады. Сезімдік қабылдау арқылы түсініктің пайда болуы және логикалық түрде түсініктен ұғымға жалпылау мен абстракцияның көмегі арқылы жету (оқушы 3 санын қалай қалыптастырады) . 1) кезеңде әртүрлі нақты жиындармен танысады {3 алма, «үшбұрыш», үш аю, үш жапырақ} . . . бұлардың әртүрлі қасиеттеріне назар аударады. «Көру» процесі бала санасында бейнелеудің ерекше формасын қабылдайды (сезінеді), объектіні сезімдік түйсіну - танымның ең алғашқы сатысы, ол ұғымға сәйкес қалыптасады.
- Мектеп математикасы курсында математикалық ұғымдарды қалыптастыру әдістемесі
Жоспары
1. Математикалық ұғым деген не?
- Математикалық ұғымдарды нақты - индуктивтік әдіспен ендіру.
- Математикалық ұғымдарды абстрактілі - дедуктивтік әдіспен ендіру.
- Математикалық ұғымдарды меңгеру.
- Ұғымдарды анықтаудан пайда болатын қателер.
- Жаңа ұғымдарды ендіруде пайда болатын қателер.
- Қорытынды.
- Ұғымды тұжырымдау схемасын еске түсірелік: қабылдау - сезіну - түсінік- ұғым.
Нақты - индуктивтік әдіспен ұғымды ендіруде оқыту процесінің негізгі кезеңдері мыналар:
- берілген ұғымның қажеттігін көрсететін (қабылдау - сезіну) практикалық мысалдар келтіру;
- берілген ұғымның маңызды және өте маңызды емес белгілерін анықтайды (оқушылар) және берілген ұғымды белгілейтін термин ендіреді (мұғалім) . Ол үшін қабылдаудан (сезіну) түсінікке өтетін өтпелі кезең керек, берілген ұғымды белгілейтін терминнің дәлелі қажет (мұғалім) ;
- берілген ұғымның барынша маңызды қасиеттері таңдап алынады және осы ұғымның анықтамасы тұжырымдалады (оқушылар) ; бұдан соң оған мұғалім дәл анықтама береді, мұны оқушылар қайталайды. Бұл үшін арада түсініктен ұғымға ауысатындай жағдай болуы керек.
- Арнайы бөліп алынатын ұғым нақты мысалдармен көрсетіледі, контр мысалдар келтіріледі және символдық белгілеуі көрсетіледі (оқушы және мұғалім) . Бұл ұғымның пайда болуын білдіреді.
- Бұдан соң оқушылар басқа ұғымға мүмкін болатын басқа анықтама береді. Бұл ұғымның меңгерілуі болады.
- Абстракты - дедуктивтік әдіспен оқушыларды оқытудың негізгі кезеңдері келесілер болып табылады:Ең алдымен жаңа ұғымға анықтама беріледі, бұл үшін оны белгілеуші термин дәлелденеді. Бұдан соң ұғым ендірілген өрнектің жеке және ерекше жағдайлары қарастырылады. Контур мысалдар келтіріледі. Келесі кезекте ендірілген ұғым нақты мысалдар арқылы иллюстрацияланады. Соңында ендірілген ұғымның қосымшасы үшін мысалдар келтіріледі.
- Сабақта оқушыларға берілген жаңа ұғымның меңгерілгенін қалай білуге болады?
Егер ұғым меңгерілген болса, онда оқушы
- ұғымның көлемі мен мазмұны туралы толық түсінігі болады;
- математикалық іс-әрекеттің барысында ұғымды қолдана біледі.
- жаңа жағдайларда өзінің білімі мен тәжірибесін қолдана біледі.
Мысалдар келтіру.
- Ұғымның анықтамасынан оқушылар қателіктер жібермеуі үшін олар анықталған және анықтаушы ұғымдарды ажырата білуі керек.
Анықтама: Анықталатын объектіге сәйкес келетін ұғым анықталған ұғым деп аталады. Анықталатын объектінің мазмұнының көмегімен ашылатын ұғым анықтаушы деп аталады.
Сонымен бірге оқушылар ұсынылған анықтаманың маңызды талаптарын білуі керек:
- Кез келген анықтама өлшемде болуы, яғни анықталушы объектінің көлемі анықталған ұғымның көлеміне тең болуы керек. Қате анықтамалардың мысалдарын келтіру керек.
- Анықталушы ұғымды сол ұғымның өзімен тікелей анықтауға болмайды.
- Анықтамалар мүмкіндігіне қарай объектіні керісінше анықтамауы керек. Мысалдар.
- Жаңа ұғымды ендіру барысында мұғалім оның белгілеріне назар аудару керек. Егер мұғалім ұғымның анықтама- тұжырымдап, кітаптағы берілген сызбалы көрсетумен шектелсе, онда оқушылар бұл ұғымды дұрыс меңгермейді.
Математикалық ұғымдарды саналы түрде меңгеруге мақсатты түрде қойылатын ауызша жаттығулар мен сұрақтар жүйесінің зор маңызы бар. (Оқушыларға қате айтылатын анықтамалардан мысалдар келтіру) .
- Оқушылар жіберген қателерді түзеткеннен гөрі алдын-ала сақтандыру жұмысын жүргізген дұрыс. Ол үшін:Жаңа ұғымды формальді ендірмеу керек; Оқушыларды ұғымдардың анықтамасын өз бетінше үйренуге баулу керек. Ендірілген ұғымның. Сөздің, анықтаманың дәлелдерін табу (келтіру) . Сабақтың соңында осы сабаққа қажетті ұғымның анықтамасын қайталау; Жаңа ұғым мен ескі ұғымның арасындағы байланысты орнату; Анықтамаларды анық, дәл, қысқа, қатаң тұжырымдауды талап ету; 1-6 пункттерін кездейсоқ жағдайда емес, қайта біртіндеп орындау керек.
- Қажетті және жеткілікті шарттар
Жоспар
- Қажетті шарттар; жеткілікті шарттар.
- Қажетті және жеткілікті шарттар.
- Теореманың түрлері және олардың байланысы.
- Келесі пікірді қарастыралық:
Сөзбе-сөз тұжырымдау. Тұжырымдалады:
- Егер натурал сан жұп болса, 1)
онда ол 6-ға бөлінеді. (Л)
- Егер натурал сан 6-ға бөлінсе, 2)
онда ол жұп (Л)
- Егер натурал сан жұп болса, 3)
онда ол 2-ге бөлінеді (И)
- Егер натурал сан 2-ге бөлінсе, 4)
онда жұп болғаны
Осы пікірлерді былайша қайта тұжырымдайық:
- Натурал сан 6-ға бөлінуі үшін оның жұп болуықажетті.
- Натурал сан болуы үшін ол 6-ға бөлінуіжеткілікті.
- Натурал сан 2-ге бөлінуі үшін ол санның жұп .
- Натурал сан жұп болуы үшін ол санның 2-ге .
Қандай шарт қажетті , ал қандай жеткілікті екенін қалай білуге болады?
Анықтама .
Егер
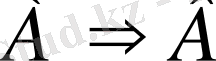 пікірі ақиқат болса, онда
пікірі ақиқат болса, онда
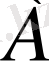 пікірі
пікірі
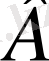 үшін қажетті шарт деп аталады.
үшін қажетті шарт деп аталады.
Егер
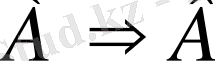 пікірі ақиқат болса, онда
пікірі ақиқат болса, онда
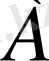 үшін
үшін
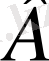 пікірі жеткілікті шарт деп аталады.
пікірі жеткілікті шарт деп аталады.
- Қажетті және жеткілікті шарттар математикада барынша қызғылықты болып есептеледі.
Анықтама . Егер
және
импликациялары бір мезгілде ақиқат болса, онда
шарты
шартының қажетті және жеткілікті шарты деп аталады, яғни
эквиваленттілік орындалады.
Мұғалім математика курсындағы «қажетті және жеткілікті шарттар» деген сөздер олардың синонимдерімен ауыстырылатынына оқушы назарын аудару керек.
- Ақиқаттығы тікелей дәлелдеу (талқылау) арқылы көз жеткізілетін математикалық сөйлем теорема деп аталады.
Теоремада мыналар анық көрсетілуі керек:
- белгілі бір объектілер (теореманың шарты) қандай шарттарда қарастырылады.
- Бұл объект туралы не тұжырымдалады «теореманың қорытындысы) .
Теореманың шарты мен қорытындысын оңай анықтау үшін оны логикалық жалғауды қолдана отырып «егер, . . . , онда . . . , » деген импликация түрінде жиі тұжырымдалады. Мысалы, «параллелограмның диагоналдары қиылысады, және қиылысу нүктесінде қақ бөлінеді» деген теореманы былай тұжырымдауға болады:
- Егер төртбұрыш параллелограм, онда оның диагоналдары қиылысады және қиылысу нүктсінде қақ бөлінеді.
- Егер төртбұрыштың диагоналдары қиылысып және қиылысу нүктесінде қақ бөлінсе, онда бұл төртбұрыш - параллелограмм.
- Егер төртбұрыш параллелограмм болмаса, онда оның диагоналдары қиылысады және қиылысу нүктесінде қақ бөлінбейді.
- Егер төтбұрышта диагоналдары қиылысып және қиылысу нүктесінде қақ бөлінбесе, онда бұл төртбұрыш - параллелограмм емес.
Енді айтылған теоремалардың түрлерін қарастырайық.
- Туцра теорема:
- Кері теорема:
- Қарама-қарсы теорема:
- Контрапозитивтік теорема:
1-4 теоремалардың барлығы ақиқат, бірақ бұлай әрқашан бола бермейді. Мысалы, вертикаль бұрыштар тең. Егер мұны 1-4 сияқты тұжырымдасақ бұлардың бәрі бірдей ақиқат бола бермейді.
Лекция 2
Математикалық оқытудағы анализ бен синтез
Жоспары
- Анализбен синтездің сипаттамасы.
- Психологиялық көзқарас бойынша қарастырғандағы анализбен синтез.
- Анализбен синтездің байланысы және ойлау процесіндегі салыстыру.
- Математиканы оқыту процесіндегі анализбен синтез (мысалдар) .
4. Математиканы оқытудағы анализбен - синтез
- Анализбен синтездің сипаттамасы
Ғылыми зерттеу әдісі ретінде - анализбен синтез математикалық зерттеулерде ерекше маңызды роль атқарады.
Анализ - логикалық тәсіл, зерттеу әдісі ретінде үйренілетін объектіні
ойша (не прак. ) құрамды бөліктерге жіктейді (белгілері, қасиеттері, қатынасы), әр бөлік бүтіннің бөлік ретінде жеке зерттеледі. (Анализ - грекше analygts - жіктеу, бөлшектеу, талдау) . Кейін себепті бірлікте, бүтін ретінде қаралады.
Жіктеу арқылы пайда болған тізбек сөйлемі
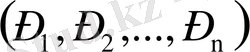 бұрыннан белгілі аксиомаға, анықтамаға, бұрын дәлелденген теоремаға келеді. Тізбектің соңғы сөйлемі
бұрыннан белгілі аксиомаға, анықтамаға, бұрын дәлелденген теоремаға келеді. Тізбектің соңғы сөйлемі
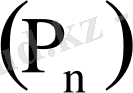 дәлелдемекші пікір болып шығады. Әрине тізбектің сөйлемі өзара белгілі қатыста болатыны айқын.
дәлелдемекші пікір болып шығады. Әрине тізбектің сөйлемі өзара белгілі қатыста болатыны айқын.
Әрине, фигураны оқығанға дейін ол туралы азды-көпті біліміміз болады. Мәселен параллелограм, дөңес көпбұрыш, тұйық фигура, жазықтың бөлігі тұйықталған сынық, қабырғалары санаулы екі қабырғасының ортақ бір нүктесі бар т. б.
Ендігі мақсат, осы мағлұматтар ішіндегі ерекше сипаттың параллелограмға тиістісін іріктеп алу, басқаша айтқанда оның қасиеттерін білу. Олар:
- #, дөңес төртбұрыш;
- диагональдары қиылысу нүктесінде қақ бөлінеді; диагональдары параллелограмды тең екі-қа бөледі.
Анализ түрі объект түріне және алға қойған мақсатқа байланысты. Кейде бүтінді бөліктерге жіктеп, бөліктерді жеке-жеке тану немесе түгел тану мәселесі қойылады.
Сөйтіп бүтіннің қасиеті танылады. Белгісізден белгіліге қарай жүретін ой өрісін де анализ деп түсінеміз.
Синтез - логикалық тәсіл, бүтіннің бөліктері қайтадан бір бүтінге бірік-
тіріледі.
Синтез (грекше sinthess - біріктіру, құрастыру, теру) - анализ процесінде бөлшектенген объектінің бөліктерін, өзара әсерімен байланысын анықтап, біріктіру. Сондай-ақ, анализбен синтез жалпылау, дерексіздеу, салыстыру және аналогиямен астарласа жүреді. Математиканы оқытудағы анализбен синтез мәні өте зор, ол есептер шешу әдісі ретінде, теорема дәлелдеу, математикалық ұғымдардың қасиетін үйрену т. б. барынша әр алуан формада кездеседі.
Анализбен синтез - іс-жүзінде бірін-бірі толықтыратын бір тұтас аналитикалық - синтетикалық әдіс . Мәселен, анализ кезінде күрделі есептер жай есептерге бөлшектенеді, ал синтез мұндай жай есептерді бір ғана
мағыналы, бір тұтас бір есепке біріктіреді. Анализді бүтіннен оның құрамды бөліктеріне жіктейтін ойлау әдісі, ал синтез-ұсақ бөліктерді бір бүтінге біріктіретін ойлау әдісі деп түсінеміз. Бала ойыншықты ұсақтап (анализ) қайта құрастырса (синтез) бұл өзіндік анализбен синтез болады.
Анализбен синтез физика - химия сияқты экспериментальды ғылымдарда кеңінен қолданылады.
Рене Декарт (1596-1650) өзінің «Логика» деген кітабында анализ-синтез әдістің мәнін тәпіштеп зертеді, осы әдістердің мәні туралы барынша көрнекі мынадай мысалдар келтіреді. Мен Кароль Карл Великийдің туысымын ба жоқ па? Деген сұрақтың жауабына екі жолмен көрнекі жауап беруге болады.
Менен Ұлы Карлға дейін және Ұлы Карлдан маған дейін туысқан болсақ, онда біз Карл екеуміз туысқанбыз. 1-анализ, 2-і синтез.
Бұл әдістердің мысалы ретінде арифметикалық, алгебралық текстілі (мазмұнды) есептер жатуы мүмкін.
Екі баланың жастарының қосындысы 12. Майгүл 5 жаста. Азат неше жаста?
1)
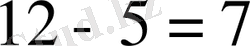 - синтезге, берілгенге негізделген.
- синтезге, берілгенге негізделген.
2)
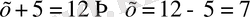 - анализге негізделген.
- анализге негізделген.
Анализ (аналитикалық) зерттеу әдісі ретінде объектінің саны мен өлшеміне сүйеніп объектінің сандық қасиетін құрастыратын жақтарын үйренеді.
Синтез (синтетикалық) - зерттеу әдісі ретінде объектінің саналық қасиетін үйренуге негізделеді. Бұдан былай анализды салдардан себепке көшетін ойлау формасы ретінде, ал синтезді себептен салдарға көшетін ойлау формасы деп түсіну керек.
- Психологиялық көзқарас бойынша ойлағандағы анализбен синтез
Математиканы оқыту процесінде әдетте анализбен синтез материалды түсінудің 2-стадиясы.
Жоғарыда анализ-синтезді ғылыми зерттеу әдісі және дербес жағдайларда оқу материалын үйренудің әдісі ретінде қарастырдық. Анализ-синтез ойлау процесінің ерекше формасы, яғни ойлаудың маңызды психологиялық сипаттамасы.
Психологиялық көзқарас тұрғысынан алғанда «Ойлау процесі - анализдеумен бөлінетін талдау және синтездеу, бұдан соң осылардан туындайтын абстракция мен жалпылау болып табылады» (Рубинштейн С. Л. О мышлении и путях его исследования М., 1958) . Бұл процестің өзіне тән заңдылығы олардың бір-бірімен өзара ойлаудың негізгі заңдылығы бойынша байланысуында. Көптеген психологиялық зерттеулердің көрсеткеніндей анализ әр түрлі формада кездеседі.
Мәселен :
а) «фильтр» типті анализ.
б) синтез арқылы болатын анализ.
а) Фильтр типті анализ кезінде есеп шешуші есепке ешбір көрінерлік жүйесіз кіріседі, ол жай ғана берілген есептің шешу әдісін қалай болса, солай жобамен іздейді, бір тәсілдің артынан екіншісін қолданып қисынсыз байқап көрулерді електен өткізген сияқты шығарып тастайды.
Жасалған болжамдар мен байқап көрулер - анализдің өзіндік формасы. Басқа сөзбен айтқанда кез келген байқап көрулер тікелей табыстарға жеткізбеген секілді толық шешімге әкелуге дайындық болады. Бұл болжаулар психологтардың зерттеулерінде өзінің шешімін тапты. Әсіресе тапқырлықты қажетсінетін есептерді шешу процесін зерттегенде есеп шешушіден тапқырлық қабілетті талап ететін ой жүгіртулердің, байқап көру әрекеттерінің ерекше пайдасы бар. Есеп шарты тудыратын қиындықтарды жеңе отырып тапқарлық анализге сүйенетінін зерттеулер көрсетті. Мәселен 6 сіріңкеден 4 тең қабырғалы
 жасау керек. Бұл есептің бас қатырғыш шешуге қиын болатыны есеп шешушіге ізделінді фигура жазықтықтың бетінде салынуы керек деп ойлайтыны, сонымен бірге есеп шешуін іздеудің дұрыс бағыты бұл
жасау керек. Бұл есептің бас қатырғыш шешуге қиын болатыны есеп шешушіге ізделінді фигура жазықтықтың бетінде салынуы керек деп ойлайтыны, сонымен бірге есеп шешуін іздеудің дұрыс бағыты бұл
 -ды кеңістікте салу керек (тетраэдр) деген ойды тудырады. Ең алдымен есеп шешуші жазықтықта әр түрлі тексерулермен есептің шешуін іздейді, бұдан соң «кенеттен» үш өлшемді кеңістікке шығу мүмкіндігін табады.
-ды кеңістікте салу керек (тетраэдр) деген ойды тудырады. Ең алдымен есеп шешуші жазықтықта әр түрлі тексерулермен есептің шешуін іздейді, бұдан соң «кенеттен» үш өлшемді кеңістікке шығу мүмкіндігін табады.
Байқап көріп, болжаулар жасау тек есептер шешуде қолданылып қоймай басқа әдістердің қолданылуына да көмектеседі.
б) Синтез арқылы болатын анализге тоқталайық.
Бұл ерекше бүкіл әрекеттің жетекші буыны ретіндегі анализ. Сондықтан ойлау процесінің бұл компонентіне ерекше тоқталайық.
С. Л. Рубинштейн былай деп жазады:
«Қысқаша және жалпы айтқанда, бұл анализдің негізгі формасы, негізгі нервтің ойлау процесі ретінде келесілермен сипатталады. Ойлау процесінде объектіге барлық жаңа байланыстар қосылады, осының салдарынан барлық жаңа сапалар жаңа ұғымдарда орнығады; сонымен бірге объектіден барлық жаңа мазмұндар сарқылады; ол әркез басқа қырынан көрінеді; әркез жаңа қасиеттер танытады» [371] . Ойлау процесінің бұл маңызды буынын түсіну үшін мысал келтірейік.
Мысал. Шеңберді сырттай сызылған тең қабырғалы
 -ң периметрі оның іштей сызылған
-ң периметрі оның іштей сызылған
 -тың периметрінен 2 есе артық болатынын дәлелдеу керек. (VIII кластың математика үйірмесінде берілген есеп) .
-тың периметрінен 2 есе артық болатынын дәлелдеу керек. (VIII кластың математика үйірмесінде берілген есеп) .
1)
 қарастырайық;
қарастырайық;
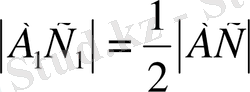 болатынын дәлелдеу керек.
болатынын дәлелдеу керек.
Сол сияқты 2)
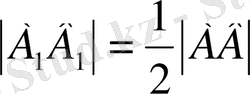 ,
,
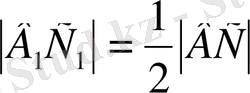
3) (1), (2) пункттерден
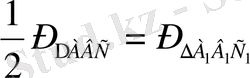
Есепті шешу барысында оқушы
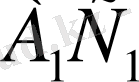 кесіндісінің қасиеттерін талдайды. Есеп шарты бойынша (
кесіндісінің қасиеттерін талдайды. Есеп шарты бойынша (
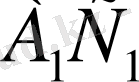 - түзуі
- түзуі
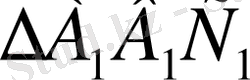 үшбұрышының бір қабырғасы) және
үшбұрышының бір қабырғасы) және
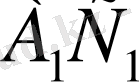 //
//
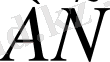 екенін бөліп алады. Бұдан соң үшбұрыштың бұл
екенін бөліп алады. Бұдан соң үшбұрыштың бұл
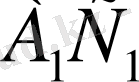 қабырғасы
қабырғасы
 -ның орта сызығы ретінде қарастырылады, бұдан жаңа қасиет бөлініп алынады:
-ның орта сызығы ретінде қарастырылады, бұдан жаңа қасиет бөлініп алынады:
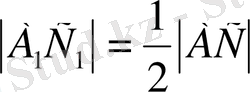
Бұдан әрі
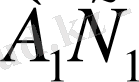 қабырғасы
қабырғасы
 -ның орта сызығы емес,
-ның орта сызығы емес,
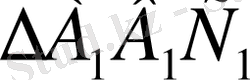 -ның бір қабырғасы
-ның бір қабырғасы
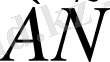 -ға # түзу ретінде қарастырылады.
-ға # түзу ретінде қарастырылады.
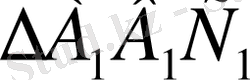 -дің бір қабырғасы ретінде қарастырылады.
-дің бір қабырғасы ретінде қарастырылады.
Сонымен есеп шығарушыға әркез
 -тың бір ғана
-тың бір ғана
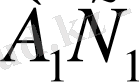 қабырғасы жаңа байланыстар жүйесі - жаңа қасиеттер пайда болады (бірде орта сызық, бірде
қабырғасы жаңа байланыстар жүйесі - жаңа қасиеттер пайда болады (бірде орта сызық, бірде
 -ң бір қабырғасы) (
-ң бір қабырғасы) (
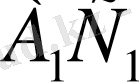 қабырғасының бөлініп алынған бұл қасиеттері бір-бірімен белгілі арақатынаста болады, бұл қатыстар есеп) .
қабырғасының бөлініп алынған бұл қасиеттері бір-бірімен белгілі арақатынаста болады, бұл қатыстар есеп) .
? 9-бет жоқ
?
?
?
- Математиканы оқытудағы анализбен синтез
Анализбен синтез математиканы оқып-үйренудің аса маңызды әдістері болып табылады. Олардың қолдануларын көрсететін мысалдар қарастырамыз:
- Теоремаларды аналитикалық және синтетикалық жолмен дәлелдеу әдістері.
Мысалы. Үшбұрыштың ішкі бұрышының қосындысы
 болатынын дәлелдеу керек.
болатынын дәлелдеу керек.
- Дәлелдеу тәсілі (аналитикалық жолмен)
- жазық бұрыш кез келген үшбұрыштың үш бұрышы жазық бұрышқа орналасатынын көрсету керек.
а)
нүктесінен өтетін
болатын жазық бұрышты саламыз.
б)
жазбадан бірден табылады.
в)
,
,
- қиюшы.
г)
,
,
- қиюшы.
д)
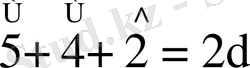
е) бірдей бұрыштарды ауыстырып
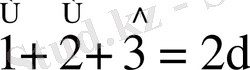
- Дәлелдеу тәсілі (синтетикалық жолмен)
а)
жүргіземіз.
б)
,
,
- қиюшы.
в)
,
,
- қиюшы.
г)
жазық бұрыш
д)
((б), в) - ларға сүйеніп)
Мысал. Тізбекті дәлелдеу керек.
,
,
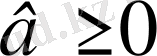
Аналитикалық метод Синтетикалық метод
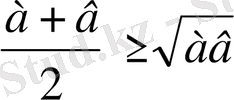
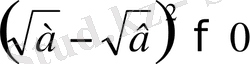
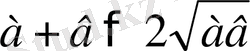
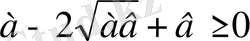
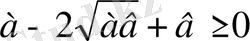
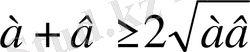
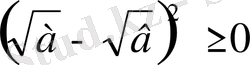
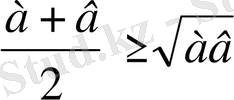
? 12-бет жоқ
?
?
?
келдік, демек алғашқы тұжырым дұрыс. Жасалған қорытынды дұрыс емес. Бұл арада жіберілген логикалық қателіктің себебі қолданылған «қорытынды ереженің» дұрыс еместігінде.
Көбінесе практикада біртіндеп екі әдісті қолданады, аналитикалық жолмен тұжырымды байқайды, сонан соң синтетикалық жолмен дәлелдеуге тиісті дәлелдейміз. Қос импликацияны пайдаланып ойлаудың екі әдісімен бірақ жазамыз:
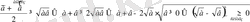 .
.
- Біртіндеп талдау әдісі.
Бұл анализдің негізгі мәні мынадай ойлауға негізделген:
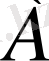 тұжырымының дұрыс болуы үшін
тұжырымының дұрыс болуы үшін
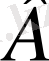 -ның дұрыс болуы қажет.
-ның дұрыс болуы қажет.
Мысал . Ромбының диагоналдары өзара ⊥ болатынын дәлелдейік.
Дәлелдеу: а)
екенін көрсету үшін
болатынын көрсету жеткілікті.
б)
болатынын көрсету үшін
-
-ға биіктік екенін көрсету жеткілікті.
в)
-
- биіктік екенін көрсету үшін
теңбүйірлі екенін көрсету керек,
- оның медианасы.
г)
тең бүйірлі болу үшін
дәлелдедік.
д) бірақ
 шарт бойынша тең,
шарт бойынша тең,
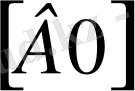 - медиана, сонымен
- медиана, сонымен
 . (парал. диаг. қас. )
. (парал. диаг. қас. )
Бұл теореманың дәлелдеудің синтетикалық методпен дәлелдену схемасы:
а)
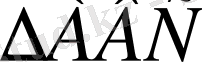 :
:
 (шарт бойынша)
(шарт бойынша)
б)
 парал. қас.
парал. қас.
в)
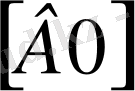 - медиана
- медиана
г)
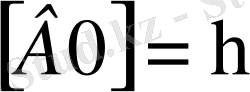
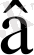
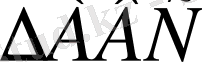
д)
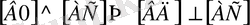 . Салыстыра келіп біртіндеп талдау методының артықшылығын байқаймыз. а) Саналы және өз бетінше, б) логикалық ойлау, в) сапалы мақсаты айқын, д) дәлелдеу методы қарапайым.
. Салыстыра келіп біртіндеп талдау методының артықшылығын байқаймыз. а) Саналы және өз бетінше, б) логикалық ойлау, в) сапалы мақсаты айқын, д) дәлелдеу методы қарапайым.
- Геометриялық салу есептерін шешуге анализ-синтез методын қолдану
Мысалы
. радиусы
 шеңберге сырттай сызылатын гипотенузасы
шеңберге сырттай сызылатын гипотенузасы
 -ға тең тік бұрышты
-ға тең тік бұрышты
 салу керек.
салу керек.
Анализ . Есеп шешілді, суретін салайық.
а)
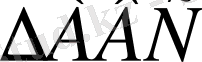 саламыз, егер
саламыз, егер
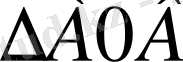 - ны салсақ;
- ны салсақ;
б)
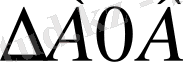 саламыз.
саламыз.
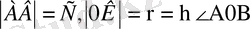 ;
;
в)
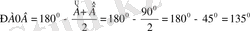 .
.
г)
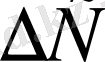 ,
,
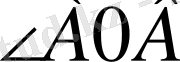 ,
,
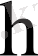 бойынша
бойынша
 саламыз:
саламыз:
Синтез
.
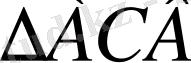 - ны саламыз, алдымен
- ны саламыз, алдымен
 :
:
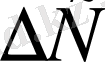 ,
,
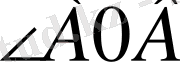 ,
,
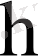 .
.
- Анализбен синтезді стереометрия есептерін шешуге қолдану
Мысалы
, призманың табаны ұзындығы
 болатын тең қабырғалы
болатын тең қабырғалы
 . Бүйір қабырғасы
. Бүйір қабырғасы
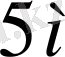 , ол табан қабырғаларымен
, ол табан қабырғаларымен
 бұрыш жасайды. Призма көлемін табу керек.
бұрыш жасайды. Призма көлемін табу керек.
Берілгені
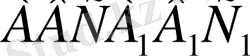 - үшбұрышты призма.
- үшбұрышты призма.
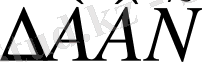 :
:
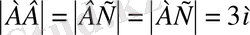
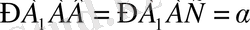 ,
,
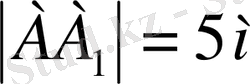
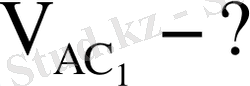
Аналитикалық әдіс : Призма көлемі
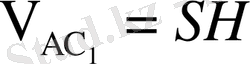 (1),
(1),


:
(2)
:
,
және
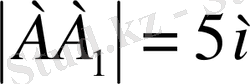
Бұл арадан
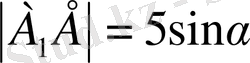 (3),
(3),
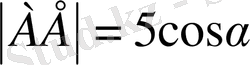 (4)
(4)
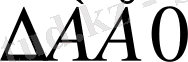 :
:
 ,
,
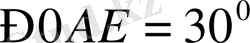
Бұлардан
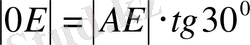
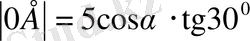 (5)
(5)
(3) және (5) мәнін (2) -ге қойсақ,
 ,
,
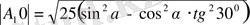

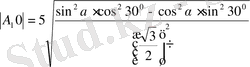
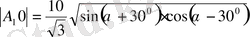 (6)
(6)
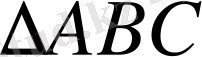 -ның ауданын табу үшін оның қабырғасының ұзындығын табу керек.
-ның ауданын табу үшін оның қабырғасының ұзындығын табу керек.
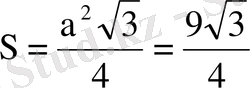 (7) .
(7) .
(6) мен (7) мәндерін (1) -ге қойып
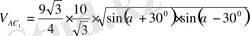
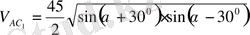 куб бірлік.
куб бірлік.
Синтетикалық әдіс . Қосымша салу жұмысын жүргіземіз:
а)
 - биссектриса
- биссектриса
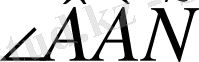 -ның.
-ның.
б)
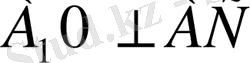 және
және
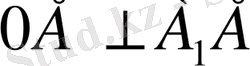 , үш
, үш
 туралы теорема бойынша
туралы теорема бойынша
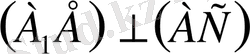
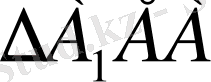 :
:
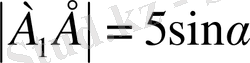 (1)
(1)
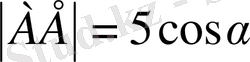 (2)
(2)
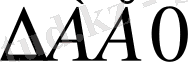 :
:
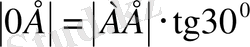
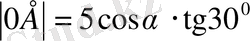 (3)
(3)
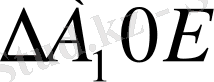 :
:
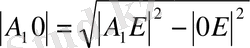 (4)
(4)
(1) және (3) мәнін (4) -ке қойып
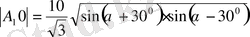
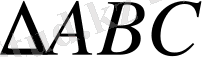 :
:
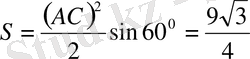 .
.
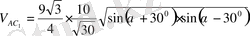 ,
,
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz