Функцияның шегі: анықтамалары, біржақты шектер және негізгі қасиеттері


Реферат
Тақырыбы: Функцияның шегі.
Орындаған:
Қабылдаған:
Тараз
Жоспар:
Кіріспе.
1. Функцияның шегі.
2. Шек. Шектің негізгі қасиеттері.
3. Біржақты шектер.
Қорытынды.
Пайдаланған әдебиеттер.
Кіріспе
Ежелгі дәуір математиктері (Евклид, Архимед) аудандар мен көлемдерді табу үшін шын мәніндегі шексіз қатарларды пайдаланған. “Жинақтылық” терминін шотланд математигі және астрономы Дж. Грегори (1638 - 1675) қатарлар үшін қолданды (1668) . 18 ғ-да жинақтылық ұғымы шашыраңқы қатарларды талдауда кеңінен қолданыла бастады (Л. Эйлер) . Қатарлардың жинақтылықтығын зерттеудің дәлірек әдістері 19 ғ-да жасалды (О. Коши, Н. Абель, Б. Больцано, К. Вейерштрасс, т. б. ) . Бірқалыпты Жинақтылық ұғымы Н. Абельдің (1826), Ф. Зейдельдің (1847 - 48) және Дж. Стокстің (1848) еңбектерінде тұжырымдалды. Функциялар теориясының, функционалдық анализдің және топологияның дамуына байланысты жинақтылық ұғымы одан әрі кеңейтілді.
Математикалық анализдің негізгі ұғымдарының бірі - функцияның шегі ұғымы анықталады. нүктесінің ойылған e -маңайы деп, нүктесінің e-маңайынан нүктесін алып тастағанда пайда болған маңайды атайды.
Функция шегінің анықтамалары
Нақты сандар жиыны X, сол жиынның нүктесі және осы нүктесінің маңайында анықталған функциясы берілсін. функциясының нүктесінде анықталған немесе анықталмағандығы талап етілмейді, яғни нүктесі маңайына тиісті болмауы да мүмкін.
Функция шегінің анықтамасын бермес бұрын «ойылған маңай» ұғымын анықтап алайық.
Анықтама . нүктесінің ойылған -маңайы деп, нүктесінің -маңайынан нүктесін алып тастағанда пайда болған маңайды атайды.
нүктесінің ойылған
- маңайын

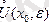 символымен белгілейді.
символымен белгілейді.
Функция шегінің екі анықтамасы бар.
1-анықтама
(Функциялардың шегінің маңайлар тіліндегі анықтамасы) . Егер кез келген E оң саны бойынша
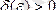 саны табылып,
теңсіздіктерін қанағаттандыратын барлық х- тер үшін
теңсіздігі орындалатын болса, онда bсанын f(x) функциясының
нүктесіндегі (
- ге ұмтылғандағы)
шегі
деп атап, келесідей белгілейді:
саны табылып,
теңсіздіктерін қанағаттандыратын барлық х- тер үшін
теңсіздігі орындалатын болса, онда bсанын f(x) функциясының
нүктесіндегі (
- ге ұмтылғандағы)
шегі
деп атап, келесідей белгілейді:
немесе
Шектің анықтамасының геометриялық мағынасы және түзулерін жүргізсек (оларды y=b түзуіне қалауымызша жақын сызуға болады), және интервалдарына сәйкес функция графигінің бөлігі сол екі түзудің арасында жатады.
2-анықтама (Функция шегінің тізбектер тіліндегі анықтамасы) .
Егер F функциясы нүктесінің маңайында анықталып, бірде-бір мүшесі - ге тең емес, шегі болатын, яғни шарттарын қанағаттандыратын, әрбір тізбегі үшін оған сәйкес тізбегінің шегі бар және ол b санына тең болса онда b нақты санын f функциясының нүктедегі шегі деп атайды.
F функциясының тізбектер тіліндегі нүктесіндегі шегін (қысқаша т. -т. )
Шектің жоғарыда берілген маңайлар тіліндегі анықтамасын, тізбектер тіліндегі анықтамасын айыру үшін,
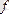 функциясының
функциясының
 нүктедегі шегінің «e-d» тіліндегі анықтамасы деп атап, «e-d»
=b символымен белгілейді.
нүктедегі шегінің «e-d» тіліндегі анықтамасы деп атап, «e-d»
=b символымен белгілейді.
Кейде шектің «e-d» және тізбектер тіліндегі анықтамаларын оларды енгізген математиктердің есімдерімен атап, сәйкесінше шектің Коши және Гейне берген анықтамалары деп атайды.
Бұл екі анықтама эквивалентті анықтамалар.
Шек. Шектің негізгі қасиеттері
Шек - математиканың негізгі ұғымдарының бірі.
- Егер алдын ала берілген кез келген ε>0 саны үшін х айнымалы шамасының белгілі бір мәнінен бастап келесі барлық мәндері х-а<ε теңсіздігін қанағаттандырса, онда а саны х айнымалы шамасының шегі (ол lіmx=а немесе х→а деп белгіленеді) деп аталады.
- Егер кез келген ε>0 аз саны үшін әрқашанда N нөмірі табылып және n>N теңсіздігін қанағаттандыратын n-нің барлық мәндері үшін xn-a<ε теңсіздігі орындалса, онда а саны айнымалы хnтізбегінің шегі (ол не n → ∞ {\displaystyle ~\infty } болғанда xn→a деп белгіленеді) деп аталады.
- Егер кез келген ε>0 аз саны үшін δ>0 саны табылып, х айнымалы шамасының х-х0<δ теңсіздігін қанағаттандыратын барлық мәндері үшін f(х) -А<ε теңсіздігі орындалса, онда А тұрақты саны f(х) функциясының х=х0нүктесіндегі шегі (ол деп белгіленеді) делінеді.
Шектердің қазіргі теориясы 19 ғ-дың басында қалыптаса бастады. Шек ұғымы алғаш рет О. Коши еңбектерінде қолданылды. Тізбек пен функция шектерінің теориясы Б. Больцано мен К. Вейерштрасстың еңбектері негізінде қалыптасты.
Жинақтылық , математикада - белгілі бір математикалық объектінің шегі болатындығын көрсететін математикалық талдаудың негізгі ұғымдарының бірі. Осы мағынада тізбектің жинақтылықтығы, қатардың жинақтылықтығы, шексіз көбейтіндінің жинақтылықтығы, үздіксіз бөлшектің жинақтылықтығы, интегралдық жинақтылық, т. б. жөнінде айтуға болады.
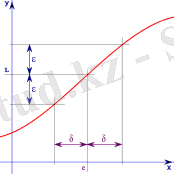
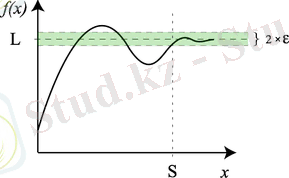
a 1 , a 2 , . . . нақты сандар тізбегінің жинақтылықтығы оның шекті шегі болатындығын көрсетеді: L оның шегі болса:lim n → ∞ a n = L {\displaystyle \lim _{n\to \infty }a_{n}=L}
деп жазылып
" a n тізбегі n шексіздікке ұмтылғанда L -ге тең" деп оқылады. Қандай да бір математикалық объектінің жинақтылық қасиеті математиканың теориялық мәселелері мен математика қолданылатын жерлерде елеулі рөл атқарады.
Қатарлар мен интегралдар теориясында абсолют жинақтылық ұғымының маңызы зор. Жинақтылық ұғымы әр түрлі теңдеулерді (алгебралық, дифференциалдық, интегралдық) шешуде (Мысалы, теңдеулердің сандық шешімдерін табу кезінде) үлкен рөл атқарады.
Шектің негізгі қасиеттері
Шектердің негізгі қасиеттері мектептегі математика курсынан белгілі:
1. Тұрақты x = c шамасыныңшегі с санының өзіне тең : lim c=c;
2. x, y, …, zсаны шектеулі және әрқайсысының ақырлы шегі бар айнымалы шамалар болсын. Сонда төмендегідей тұжырымдар орынды:
а) Олардың алгебралық қосындысының (атап айтқанда, қосындысы мен айырымның) да шегі бар және ол шектердің қосындысына (айырымына) тең:
lim(x± y ±… ± z) = limx ± limy…±limz;
в) Олардың көбейтіндісінің шегі шектердің көбейтіндісіне тең:
lim(x*y *…*z) = limx * limy *…*limz.
3 . u және ɸ айнымалы шамаларының шектері бар және lim ɸ = 0 болмағанда, осы айнымалылардың қатынасының да шегі бар болады; lim =
Біржақты шектер
Біржақты шектер
шегінің анықтамасында саны нүктесінің қай жағында орналасқаны туралы ештеңе айтылған жоқ. Ол нүкте үшін және теңсіздіктерінің әрқайсысы орындалуы мүмкін.
Мұндай шекті жай немесе екіжақты деп атайды.
Егер шектің анықтамасына қосымша немесе шартын енгізсек, онда сәйкес оң немесе сол жақты шектің анықтамасына келеміз.
Анықтама. функциясы интервалында анықталсын.
Егер кез келген саны бойынша саны табылып, теңсіздігін қанағаттандыратын барлық x- тер үшін f(x) -b<e теңсіздігі орындалса, онда b санын f(x) функциясының нүктесіндегі сол жақты (оң жақты) шегі деп атайды.
Оң және сол жақты шектерді біржақты шектер деп атап,
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz