Сызықтық функцияны оқыту әдістемесі

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ..2.3

І. СЫЗЫҚТЫҚ ФУНКЦИЯНЫ ОҚЫТУ ӘДІСТЕМЕСІ
1.1. Функцияның шығу тарихы ... ... ... ... ... ... ... ... ... ... ... ... .4.5
1.2. Оқушыларда функция туралы ұғым қалыптастыру. Функцияның формуламен берілуі ... ... ... ... ... ... ... ... ...6.7
1.3. Функцияның кестемен және графикпен берілуі ... ... ... ... ... ...8.9
1.4.Сызықтық функцияны оқыту оның графигін салуға үйретy...10.11
1.5.Сызықтық функцияның дербес жағдайларындағы графиктерін оқыту ... ... ... ... ... ... ... ... 12.13
1.6.Сызықтық функцияның графиктерінің өзара орналасуын оқыту ... ... ... ... ... ... ... ... ... 14.16
II. Сабақтың тақырыбы: Сызықтық функциялар графиктерінің өзара орналасуы ... ... ... ... ... ... ... ... ... ...17.26

ҚОРЫТЫНДЫ ... ... ... ... ... ... ... ... 27

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... ... ..28

Тақырыптың өзектілігі: Еліміздің білім беру ісін жаңартудың негізгі түпкі мақсаттары мен бағыттары Қазақстан Республикасы орта білім стандартында көрініс тапқан. Мемлекеттік білім стандарты біліміміздегі мемлекеттік норма ретінде қабылданатын параметрлер жүйесі болып табылады. Қазіргі заман көшінен қалып қоймай, уақыт талабына сай жас ұрпаққа жан-жақты білім беру әр ұстаздың негізгі міндеті. Қай пәнді алсақ та оған оқушылардың қызығушылығын арттыру үшін түрлі әдістерді қолдана білуі керек. Қазіргі таңда мектептерде басқа пәндер сияқты математиканы да оқыту да өзекті мәселелердің бірі болып отыр. Базистік оқу жоспарында мемлекеттік математикалық білім стандартына сәйкес келетін оқушылардың математикалық даярлығының міндетті деңгейін қамтамасыз етуге жеткілікті уақыт қарастырылған. Еліміздің ертеңі - бүгінгі жас ұрпақ.
Сондықтанда мұғалім әрбір сабақты түрлендіріп, оны оқушылар жалықпайтындай етіп өткізуі керек.
Математика пәнін оқыту үшін ең бастысы оқыту мақсатын, өтетін тақырыптар мазмұнын анықтап алу. Математиканы оқытудан күтілетін нәтижелерді оқушының дамуын қамтамасыз ететін білім мазмұнын құрайтын әрбір жеке тақырыптың бірі – «Сызықтық функция, функция анықтамасы»
Көптеген математика оқулықтарына, оқу – әдістемелік құралдарына, баспасөз құралдарына шолу жасай отырып, тақырыптың мәнін ашып, оларды оқытып үйретудің басымдығын дәлелдеуге тырыстым.
Бұл тақырыпты игертуге оқушыларды бір – біріне көмектесуге, ұйымшылдыққа, шапшаңдылық пен жауапкершілікке баулиды. Сондықтанда оқытудың түрлі әдістерін дұрыс таңдап, оқушылардың ой-өрісін, сана – сезімін, пәнге деген қызығушылығын, ынтасын арттыру мақсатында бұл тақырыптың маңызы зор.
Математиканы оқыту процесінде танымның ғылыми зерттеу әдістері есептер шығару, математикалық ұғымның қасиеттерін оқып үйрену әдістері ретінде әртүрлі формада кездеседі.
Сондықтан математиканы оқытудың басты мақсаты қазіргі қоғамның әрбір мүшесінің күнделікті өмірі мен қызметіне қажетті аралас пәндерді үйрету мен икемділікті оқушының алуына жағдай жасау, оқушының саналы зерделі болуын қамтамасыз ету:
Зерттеудің мақсаты:
Мектеп математика курсында оқушыларды функция, сызықтық функция анықтамасымен таныстыру. Оларды шеше білуге, графигін тұрғызуға және сызықтық функцияның дербес жағдайындағы y=f(x), y=kx+l
Функцияларымен таныстырып, графигін салуды қалыптастыру.
Зерттеу міндеттері:
Мектепте функция ұғымының математикалық анықтамасын әртүрлі теориялық және практикалық бағыттағы арнайы мысалдармен
жандандыруды қажет етеді.

Негізгі әдебиеттер:
1. Математика 1-2 бөлім 6- сынып. «Атамұра» 2015ж.Алдамұратова Т., Байшоланов Т.,Байшоланов Е.
2. Математика тарихы. Алматы 1996ж. А.Собалақов.
3. 6- сынып Математикалық оқулық. Оқыту әдістемесі. Дидактикалықматеиалдар. Алматы «Атамұра» 2010 ж. Р. Базаханова, Л. Шевалова.
4. Әдістемелік нұсқау. Дидактикалық материалдар. Есептер жинағы. Алматы «Мектеп» 2009ж. Ә. Әбілқасымова, З. Жұмағұлова

Қосымша әдебиеттер:
1. Математика – 1 «Шың Алматы» 2008ж.
2. Математика журналы 2008 жыл 6-саны
3. Из опыта преподавания математики в школе
4. 6 –сынып математика оқулығы. Алдамұратова Т.А.
5. Математика. Дидактикалықматериалдар. 6 сынып. ОӘК.Алдамұратова Т., Қуандыққызы З.,Конакбаева С.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:

КІРІСПЕ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..2-3

І. СЫЗЫҚТЫҚ ФУНКЦИЯНЫ ОҚЫТУ ӘДІСТЕМЕСІ
1.1. Функцияның шығу тарихы ... ... ... ... ... ... ... . ... ... ... ... ... 4-5
1.2. Оқушыларда функция туралы ұғым қалыптастыру. Функцияның формуламен берілуі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..6-7
1.3. Функцияның кестемен және графикпен берілуі ... ... ... ... ... ...8-9
1.4.Сызықтық функцияны оқыту оның графигін салуға үйретy...10-11
1.5.Сызықтық функцияның дербес жағдайларындағы графиктерін оқыту ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... 12-13
1.6.Сызықтық функцияның графиктерінің өзара орналасуын оқыту ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... .14-16
II. Сабақтың тақырыбы: Сызықтық функциялар графиктерінің өзара орналасуы ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... ... .17-26

ҚОРЫТЫНДЫ ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... ... ... ... ... .27

ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ... ... ... ... ... ... . ... ... ... ... ... 28

КІРІСПЕ

Тақырыптың өзектілігі: Еліміздің білім беру ісін жаңартудың негізгі түпкі мақсаттары мен бағыттары Қазақстан Республикасы орта білім стандартында көрініс тапқан. Мемлекеттік білім стандарты біліміміздегі мемлекеттік норма ретінде қабылданатын параметрлер жүйесі болып табылады. Қазіргі заман көшінен қалып қоймай, уақыт талабына сай жас ұрпаққа жан-жақты білім беру әр ұстаздың негізгі міндеті. Қай пәнді алсақ та оған оқушылардың қызығушылығын арттыру үшін түрлі әдістерді қолдана білуі керек. Қазіргі таңда мектептерде басқа пәндер сияқты математиканы да оқыту да өзекті мәселелердің бірі болып отыр. Базистік оқу жоспарында мемлекеттік математикалық білім стандартына сәйкес келетін оқушылардың математикалық даярлығының міндетті деңгейін қамтамасыз етуге жеткілікті уақыт қарастырылған. Еліміздің ертеңі - бүгінгі жас ұрпақ.
Сондықтанда мұғалім әрбір сабақты түрлендіріп, оны оқушылар жалықпайтындай етіп өткізуі керек.
Математика пәнін оқыту үшін ең бастысы оқыту мақсатын, өтетін тақырыптар мазмұнын анықтап алу. Математиканы оқытудан күтілетін нәтижелерді оқушының дамуын қамтамасыз ететін білім мазмұнын құрайтын әрбір жеке тақырыптың бірі - Сызықтық функция, функция анықтамасы
Көптеген математика оқулықтарына, оқу - әдістемелік құралдарына, баспасөз құралдарына шолу жасай отырып, тақырыптың мәнін ашып, оларды оқытып үйретудің басымдығын дәлелдеуге тырыстым.
Бұл тақырыпты игертуге оқушыларды бір - біріне көмектесуге, ұйымшылдыққа, шапшаңдылық пен жауапкершілікке баулиды. Сондықтанда оқытудың түрлі әдістерін дұрыс таңдап, оқушылардың ой-өрісін, сана - сезімін, пәнге деген қызығушылығын, ынтасын арттыру мақсатында бұл тақырыптың маңызы зор.
Математиканы оқыту процесінде танымның ғылыми зерттеу әдістері есептер шығару, математикалық ұғымның қасиеттерін оқып үйрену әдістері ретінде әртүрлі формада кездеседі.
Сондықтан математиканы оқытудың басты мақсаты қазіргі қоғамның әрбір мүшесінің күнделікті өмірі мен қызметіне қажетті аралас пәндерді үйрету мен икемділікті оқушының алуына жағдай жасау, оқушының саналы зерделі болуын қамтамасыз ету:
Зерттеудің мақсаты:
Мектеп математика курсында оқушыларды функция, сызықтық функция анықтамасымен таныстыру. Оларды шеше білуге, графигін тұрғызуға және сызықтық функцияның дербес жағдайындағы y=f(x), y=kx+l
Функцияларымен таныстырып, графигін салуды қалыптастыру.
Зерттеу міндеттері:
Мектепте функция ұғымының математикалық анықтамасын әртүрлі теориялық және практикалық бағыттағы арнайы мысалдармен
жандандыруды қажет етеді. Негізгі көңіл бөлетін жағдайлар:
1. Оқушылар өздігінен функция оқып - зерттеуді оның құрамындағы x - тәуелсіз айнымалысы, f(x) - функция мәні ұғымдарының мағынасын талқылаудан құрастыру.
2. Функция ұғымын қоршаған ортадан алынған көптеген мысалдар арқылы пысықтау керек.
3. Түзу және жазықтық бойындағы координаталық жүйе ұғымдарына сүйене отырып, функция графигін функцияны көрнекі түрде бейнелеу екенін түсіндіріп, функция қасиеттері сол графиктен оқылатынына үйрету.
4. Аналитикалық зерттеу мен графиктік зерттеулер қатар жүргізілу керек.
5. Функция анықтамасы толық зерттеуді қажет ететін шешумен пысықталуы қажет.
Зерттеу объектісі:
Математиканы оқыту үрдісінде сызықтық функцияны оқыту және олардың дербес жағдайларына тоқталу, олардың графигін салуды үйрете отырып жаңа білімдерді алу тәсілдерімен қаруландырып, алған білімдерін теориялық және практикалық мәселелерді шешуге саналы түрде қолдана білу сияқты ақыл - ой белсенділігін дамыту.
Зерттеудің ғылыми болжамы:
Бұл тақырыпты меңгертіп, үйрете отырып білім сапасын жетілдіріп, оқушылардың қызығушылығын арттырып, ойлау қабілетін дамытып, ізденімпаздық пен шығармашылыққа баулитынын тұжырымдау.
Зерттеу әдістері:
oo жинақталған материалдарды сұрыптау;
oo оларды талдау;
oo әдебиеттерді зерттеу;
oo салыстыру;

І. СЫЗЫҚТЫҚ ФУНКЦИЯНЫ ОҚЫТУ ӘДІСТЕМЕСІ
1.1. Функцияның шығу тарихы

Табиғат құбылыстары мен
техника процестерін математикалық
аппарат арқылы меңгерудегі
барлық идея функциялық тәуелділік
ұғымының жөргегінде жатыр

А.Я.Хинчин
Европада капитализмнің дамуы, үйреншікті қолөнер кәсібінен машиналық техникаға көшу, халықаралық сауда жұмысының жандануы, соған байланысты кемелердің белгілі бағытпен теңіздер арқылы жүретін қатынас жолдарының күшеюі т.б. математикаға жаңа талаптар қоя бастады. Бірақ осындай өмір талаптарын орындауға бұл кезде математика дәрменсіз еді. Ол үшін математиканың өзіне келесі өзгеріс енгізу керек болды.
Математикаға осындай келесі өзгерістер енгізген - координаталар методы айнымалы шамалар мен функциялар болды.
Бұл ұғымдарды XVII ғасырдың орта кезінде математикаға енгізген француздың математигі және философы Р.Декарт деп есептелінеді, ал шынында координаталары методын ғылыми - зерттеу жұмыстарында қолдану әрекеті адам практикасында ерте пайда болды.
Көне замандағы астрономдар аспан сферасына ойша жүргізілген координаталар арқылы: жұлдызды аспанның карталарын жасады, аспан шырақтарының орындарын белгіледі. Күннің, Айдың және планеталардың қозғалмайтын жұлдыздарға қарағандағы қозғалыстарын анықтады. Кейінгі кезде жер бетінің карталарын жасау және теңізде жүрген кемелердің орнын көрсету үшін географиялық координаталар системасы пайдаланылды, бірақ XVII ғасырға дейін координаталар методын пайдалану мәселесі сыңаржақ болып келді, не ол қозғалмайтын бір объектінің (тау, орман) қалпын, немесе қозғалмалы объектілердің (кеме, планета) қалпын анықтау үшін қолданылды.
Координаталық методты пайдаланып француз математигі Н.Орем (1323-1382жж.) абсцисса мен ординатаны ендік, бойлықдеп атап графиктер сызды және Декарттан 10 жыл бұрын, Декарттың отандасы, белгілі математик Ферма өзінің Жазықтық пен кеңістіктегі орындар теориясына кіріспе (1679ж.) атты, Декарттың Геометриясынан (1637ж.) бұрын жазылып, одан көп кейін (өлген соң) шыққан кітапшасында да қолданды, бірақ Ферманың баяндау методы ұғымға ауыр және кітапшасы кешігіп шыққандықтан, қазіргіге жақын методпен (математикалық символдармен) жазылған Декарттың шығармасы кең тарап кетті.
XVI ғасырда жаратылыстану ғылымдары қозғалыстарды зерттеу мәселесімен шұғылданды. Кеплер планеталардың Күнді элипс бойымен айнала қозғалатынын тағайындады. Сөйтіп гректер үшін тек математикалық объекті болған конустық қималар (элипс, параболла, гипербола) Декарттан біраз бұрын және Декарттың тұсында реальдық мағынаға ие болды. Міне осының барлығы Декарттың табысына жол ашты.
Алғашқы функция ұғымы, геометриялық ұғымға (кесіндіге) байланысты болды. Декарт, Ньютон, Лейбниц т.б. белгілі заңдылықпен өзгеретін кесіндіні функция деп атады.
Функция аналитикалық мағына берген ағайынды Я мен И.Бернуллилер мен Л.Эйлер болды, бірақ Эйлер функцияның аналитикалық мағынасы геометриялық мағынасынан көрі тар деп есептеді.
1837 жылы француз математигі Лейбниц 1694 жылы (Гюгинске жазған хатында) Функция деген терминді бірінші рет қолданды.
XVIII ғасырдың орта кезіне дейін функцияның казіргідей арнаулы белгісі болмады. Оны f(x) түрінде математикаға 1734 жылы Эйлер енгізді. Кейін математикада жиындар теориясының өріс алуына байланысты авторлардың көпшілігі функцияға жиындар тұрғысынан қарап анықтама беретін болды.
XVII ғасырдың орта кезінде туған функция ұғымы екі ғасыр бойы мектеп программасына енбеді. Мектепте математиканы оқыту жұмысына өзгеріс енгізу жөнінде неміс математигі Ф.Клеин (1849-1925) елеулі еңбек жасады. Ол бұл жөнінде халықаралық комиссия құрды және Клеиннің басшылығымен оның идеясын іске асыратын программа (Мейрон программасы)жасалды.
Россияда орыстың белгілі методистері: Шохор-Тройцкий, Шереметевский т.б Клеиннен бұрын XIX ғасырдың ақыр кезінде-ақ мектептің математика программасына функция ұғымын мектеп курсына енгізу алгебраның ғылыми дәрежесін көтереді, алгебрамен практика мәселелерін шешу мүмкіншілігін арттырады деп функция ұғымының теориялық және практикалық маңызын дұрыс түсінді және функция ұғымын алгебра курсына енгізу мәселесіне 1911-1914 жылдар ішінде болған математика мұғалімдерінің бүкіл ресейлік I-II съездерінде көп көңіл бөлді.
Функция ұғымы мектеп программасына әуелі Францияда енді, ал революцияға дейінгі орыс мектептері программасында бұл ұғым болмады. 1918 жылы жасалған математиканың бірінші программасына функциялар мен туындылар ұғымы енді. Одан кейін математика программасы бірнеше рет өзгерді, бірақ функция ұғымы программада ылғи қалып отырды. Кейінгі жасалған орта мектептің алгебра программасынан бұрын тригонометрия курсында оқытылып келген тригонометриялық функциялар және математикалық анализден туындылар ұғымы еніп,алгебра курсында оқушыларға функция жөнінде едәуір кең білім беру мүмкіндігі туды. Алгебра курсы мазмұнының осындай молайып өзгеруі оның да әсерін тигізіп, мектептің жоғарғы кластардағы алгебра курсы алгебар және элементар функциялар деп аталады.

1.2. Оқушыларда функция туралы ұғым қалыптастыру. Функцияның формуламен берілуі

Функция ұғымының математикалық анықтамасын әр түрлі теориялық және практикалық бағыттағы арнайы мысалдармен жандандыруды қажет етеді. Функция ұғымын қоршаған ортадан алынған көптеген мысалдар арқылы пысықтап аламыз.
Техникада, шаруашылықта және күнделікті өмірде бір шаманың мәні екінші шаманың мәніне тәуелді болатынын жиі кездестіреміз.
Тәуелсіз айнымалының әрбір мәніне тәуелді айнымалының бір ғана мәні сәйкес келетін тәуелділікті функционалдық тәуелділік немесе функция деп атаймыз. Функция (функционалдық тәуелділік) жалпы мына түрде жазылады: y= f(x). Мұндағы х - аргумент, у - функция, f - функцияның аргументке тәуелділігі белгілі бір ережеге сәйкес жазылғанын білеміз.
Мектепте функцияларды оқытуды төмендегідей әдістемелік схемамен жүргізуге болады:
1. Берілген функцияға келтірілетін нақты ситуацияны (есепті) қарастыру;
2. Берілген функцияның анықтамасын тұжырымдау, функцияны формуламен беру, осы формулаға кіретін параметрлерді зерттеуді жүргізу;
3. Оқушыларды берілген функцияның графигімен таныстыру;
4. Функцияның негізгі қасиеттерін зерттеу: анықталу облысы мен мәндерінің облысы, өсуі мен кемуі, таңба тұрақытылық аралықтары, нолдері, экстремумдары, жұптығы мен тақтығы (немесе осы қасиеттердің жоқтығы), периодтылығы, үздіксіздігі, шектеусіздігі.
VIII-IX кластарда функцияның қасиеттері графигі арқылы анықталады,
яғни көрнекі түсінік негізінде, тек кейбіреулері ғана аналитикалық негізделеді, қарастырылуға тиісті қасиеттер тізімі біртіндеп артады (осыдан бастап белгілі бір нүктелері арқылы график салу қиындай бастайды) сәйкес теориялық материалға байланысты.
Жоғары кластарда функцияны зерттеу арқылы график сала бастайды.VII-IX кластарда функция қасиеттерін үш тілде графиктік, сөзбен, символикалық айтуға үйренеді. Бұл дағды бірден қалыптаса қоймайды, бірақ оның дидактикалық маңыздылығы өте зор.
5. Функцияның қасиеттерін әр түрлі есептер шығаруда, теңдеу және теңсіздік шешуде де, қолдана алу.
Бұл кезең фукнцияны өтуге байланысты негізгі ұғымдар мен теориялық
жағдайларды бекіту кезеңі, сәйкес білік пен дағдыны қалыптастыру кезеңі болып табылады.
Бұл әдістемелік схема кез келген функцияны оқыту бағдарламасы болып табылады.
Сызықтық функция y=ax+b.
y=kx+b x∈ R k, b-нақты сандар
x= - bx (k!=0) сызықтық функция шектеусіз k=0, y=kx.
Екі белгісізді сызықтық теңдеулер жүйесін оқушыларға графиктік тәсілмен шешуді үйреткен дұрыс.
Нақты функциямен тоғысу тура және кері пропорционалдықтың мысалы арқылы қарастырылады. Оны қарастыру бірнеше кезеңнен тұрады. І кезең - пропедевтикалық 5 класта енгізіледі пропорцияны құру және шешу болып табылады. Тура және кері пропорционалдықты оқып үйрену бірнеше мақсатты көздейді. Санды немесе айнымалысы бар өрнектерді теңбе-тең түрлендіру, шама ұғымын үйренуге дайындық, теңдеудің жеке түрін үйрену т.б. Негізгі мақсат 2 формуланы енгізу. y=ax2, y=ax3функциялары енгізіледі.
Оқушылар білуі тиіс:
oo Функционалдық тәуелділік туралы ұғымды;
oo Функционалдық тәуелділікте тәуелсіз айнымалының бір мәніне тәуелді айнымалының бір ғана мәні сәйкес болатындығын;
oo Функцияның анықталу аймағы, мәндерінің аймағы туралы түсінікті.
Оқушылар үйренуі тиіс:
oo Аргументтің берілген мәніне сәйкес функцияның мәнін табуды;
oo Функцияның берілген мәніне сәйкес аргументтің мәнін табуды.
Тақырыптың алдын ала даярлық тапсырмасында, оқушылар поездың
тұрақты белгілі жылдамдығы бойынша берілген уақыттағы жүрген жолын есептейді. Есептеу нәтижесінде уақыт немесе жылдамдық тәуелсіз шама, ал жол тәуелді шама екеніне көз жеткізеді.
Аргументтің берілген мәніне сәйкес функцияның мәнін табудан оқушылардың білімдерін тексеру үшін Функция мәндерінің лабиринті ойынын ойнатқан тиімді.

-5

аргумент

7
8,5

-1

8
9

f(x)=3x+52

-5
3

функция
4
16
1

14,5

Ойын шарттары: бір оське бекітілген радиустары әр түрлі (осьтен айналатын) екі дөңгелек болады. Ішкі дөңгелекте функцияның аргументінің мәні беріледі, сыртқы дөңгелекте оған сәйкес функцияның мәні беріледі. Дөңгелектердің центрінде берілген функция жазылады. Оқушы ішкі дөңгелектегі аргументтің берілген мәніне сәйкес сыртқы дөңгелектен функция мәнін тауып, оларды бір радиуста орналастырады. Оқушылардың білімі бағаланады.

1.3. Функцияның кестемен және графикпен берілуі

Функция формуламен берілгенде де аргументтің белгілі бір мәніне сәйкес функция мәнін есептеп, олардың сәйкес мәндерін кестедегі бір бағанға жазамыз.
Функция у=3х формуласымен берілсін. х=1; 2; 3; мәндерінде функция мәні f(1)=3;f(2)=6;f(3)=9болады. Енді осы функцияны кесте түрінде жазамыз.

х
1
2
3
y=f(x)
f(1)=3
f(2)=6
f(3)=9

Яғни, функция кестемен берілгенде кестенің бір жолына аргументтің мәні жазылса, екінші жолына оған сәйкес функцияның мәнін жазамыз.
1-мысал. Функция у=3х+1формуласымен берілсін. Функцияның 0; 1;
-1; 2; мәндері үшін кесте құрып жазамыз.
Ол үшін берілген мәндері үшін функцияның мәндерін есептейміз.
f(0)=1; f(1)=4; f(-1)=-2; f(2)=7;

x
0
1
-1
2
y
1
4
-2
7

2-мысал. Мына кесте түрінде берілген функцияның аргументі 4; 8 болғандағы функцияның мәнін анықтаймыз.

x
2
4
6
8
у=12(3x+1)
3,5
6,5
9,5
12,5

Функцияның аргументі 4; 8 мәндерінің сәйкес бағандарының фукциясының мәні 6,5; 12,5 болады.
3-мысал. Функцияның кесте түрінде берілгендегі функцияның мәнін табайық және формула түрінде жазайық.

Аргумент х
1
2
3
4
5
6
7
Функция у
1
4

16

36

Кестедегі бос орындағы (функция мәнін) мәнін табу үшін мынадай заңдылықты байқаймыз.
х=1болғанда у=1=1*1
х=2болғанда у=4=2*2
х=4болғанда у=16=4*4
х=6болғанда у=36=6*6
ал, х=3; 7 болғанда у= 9; 49 болады, яғни аргумент мәні өзіне көбейтіліп фунуция мәні болып тұр. Сондықтан функцияны формула түрінде у=х2 болып жазылады.
Оқушыларға білуге тиіс:
oo Функцияның графигі туралы түсінікті;
oo Функцияның графигінде аргументтің бір мәніне функцияның бір ғана
мәні сәйкес болатындығын;
Оқушылар үйренуі тиіс:
oo Функцияның формуласы бойынша оның графигін салуды.
oo Функцияның графигінен аргументтің берілген мәніндегі функцияның мәнін табуды және функцияның берілген мәніне сәйкес аргументтің мәнін табуды.
Айнымалы арасындағы функционалдық тәуелділік график арқылы берілуі мүмкін. Функцияның графигі координаталық жазықтықта салынады. Координаталар жүйесін салып (декарттық координаталар жүйесі) оның абциссалары (Ох осі) бойына функция аргументтің мәнін салып, ординаталар (Оу осі) бойына функцияның сәйкес мәндерін саламыз. Функция графигін салу үшін 2 қадамды орындаймыз:
1. Функция аргументінің белгілі бір аралығындағы мәндер кестесін құрамыз.
2. Кесте бойынша функцияның графигін саламыз.
Функцияның графигі деп координаталық жазықтықтағы абциссалары
аргументтің мәндеріне тең, ал ординаталары функцияның сәйкес мәндеріне тең нүктелердің жиынынан тұратын сызбаларды атайды.
Функцияның графигін салуға мысалдар қарастырамыз:
1-мысал. Белгілі бір функция графигі берілсін.

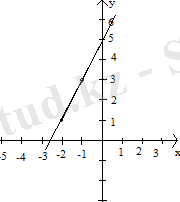
1-сурет
Осы функцияның х=-1 мәнін табу үшін абциссалар осіндегі х=-1 нүктесінен ординаталар Оу осіне параллель түзу (EN) жүргіземіз. Оның графикпен қиылысқан нүктесінен ординаталар осіне NK перпендикуляр түзуін түсіреміз К нүктесінің координатасы ізделінді y=3 мәні болады.

2.4 . Сызықтық функцияны оқыту оның графигін салуға үйрету

Оқушылар білуге тиіс:
oo Сызықтық функцияны формуламен жазуды;
oo Сызықтық функцияның графигі түзу сызық болатындығын;
oo Түзудің бұрыштық коэффицентінің оң сан немесе теріс сан болуына сәйкес сызықтық функцияның графигінің орналасуын бағдарлауды.
Оқушылар үйренуге тиіс:
oo Сызықтық функцияның графигін салуды;
oo Сызықтық функцияның графигі бойынша оны формуламен жазуды;
oo Берілген нүктенің түзуге тиісті немесе тиісті еместігін тексеруді.
Алдымен у=1,5х+6функцияларының кесте түрінде толтырып, графиктерін салайық. Мұндағы х=-1; 0; 1 нүктелері үшін толтырамыз.
у=1,5х+6 функциясы үшін:

х
-1
0
1
у=1,5х+6
4,5
6
7,5

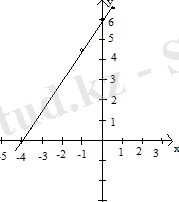
2-сурет

2-мысал. Суретте кескінделген сызықтық функцияны формуламен жазайық.

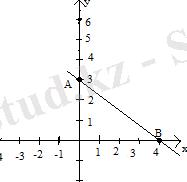
3-сурет

Түзу Оу ординаталар осін А (0;3) нүктесінде қияды. х=0; у=3 мәндерін y=kx+l формуласына қоямыз:
3=k*0+l
Онда l=3
к-ны табу үшін түзудің Ох абциссалар осімен қиылысу В (4;0) нүктесінің координаталарының (х=4; у=0) мәндерін және l=3-ті y=kx+l формуласына қоюымыз керек.
Сонда 0=k*4+4;
Осыдан k= - 34
Сонымен суретте берілген функция графигінің формуласы мына у= - 34х+3 түрінде болады.
Берілген нүктенің түзуге тиісті немесе тиісті болмауын қарастырайық.
Жоғарыда 1-мысалдағы функция графигі үшін А (4;0) нүктесі түзуге тиісті болады, себебі x=4 болғанда функцияның мәні у=0. Яғни у=0, x=4 болғанда у= - 34х+3 функциясының орнына қойғанда
0= - 34*4+3
0= 0
теңдігі орындалады. Ал С (4;1) нүктесі түзуге тиісті емес, себебі берілген функция орнына қойған теңдік орындалмайды.
1!= - 34*4+3
1!=0

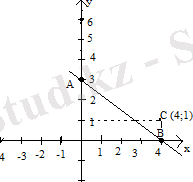
4-сурет

4.5. Сызықтық функцияның дербес жағдайларындағы графиктерін оқыту.

Оқушылар білуге тиіс:
oo Тура пропорционалдықтың формуласы мен графигін;
oo Сызықтық функцияны және оның графигін.
Оқушылар үйренуге тиіс:
oo Тура пропорционалдықтың графигін салуды және графигі ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.