Рационал және иррационал теңдеулер мен теңсіздіктерді шешу әдістері


Қазақстан Республикасы Білім және ғылым министрлігі
М. Өтемісов атындағы Батыс Қазақстан мемлекеттік университеті
Физика - математика факультеті
Физика және математика кафедрасы
Тақырыбы: РАЦИОНАЛ ЖӘНЕ ИРРАЦИОНАЛ ТЕҢДЕУЛЕР МЕН ТЕҢСІЗДІКТЕРДІ ШЕШУ ӘДІСТЕРІ
Курстық жұмыс
Орындаған:
Тексерген: жаратылыстану ғылымдарының
магистрі
Орал, 2016 жыл
МАЗМҰНЫ
КІРІСПЕ . . . 3
1 РАЦИОНАЛ ЖӘНЕ ИРРАЦИОНАЛ ТЕҢДЕУЛЕР
1. 1 Рационал өрнек және оның қарапайым түрі . . . 6
1. 2 Безу теоремасы. Көпмүшеліктердің түбірлері . . . 8
1. 3 Бөлшек - рационал теңдеулер . . . 10
1. 4 Түрлендіру әдістерімен теңдеулерді шешу әдістері . . . 13
1. 5 Бір айнымалылы бүтін рационал теңдеулер . . . 16
1. 6 Иррационал теңдеулер . . . 18
1. 7 Иррационал теңдеулерге мысалдар . . . 22
2 РАЦИОНАЛ ЖӘНЕ ИРРАЦИОНАЛ ТЕҢСІЗДІКТЕР
2. 1 Теңсіздіктер. Мәндес теңсіздіктер . . . 24
2. 2 Рационал теңсіздіктерді шешу әдістері . . . 25
2. 3 Модулі бар теңсіздіктер . . . 27
2. 4 Иррационал теңсіздіктерді шешу . . . 29
ҚОРЫТЫНДЫ . . . 33
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . . 34
КІРІСПЕ
Орта мектепте математикалық білімдер жүйесін оқытуда теңдеулер мен теңдеулер жүйелерінің орны ерекше. Теңдеулер мен теңдеулер жүйелерін терең түсініп меңгеру математикалық білімдерді одан әрі дамытуға, қоршаған ортадағы сан алуан құбылыстарға, терең мағыналы модельдер жасауға үйретеді. Олай болса, теңдеулер мен теңдеулер жүйелерінің теориялық және практикалық маңызы зор.
Математика оқулықтарында теңдеулер мен теңсіздіктерге байланысты материалдар мектеп математика курсының қомақты бөлігін құрайды, себебі теңдеулер мен теңсіздіктер математиканың түрлі салаларында және маңызды қолданбалы есептерді шығаруда кең қолданыс табады.
Теңдеу мен теңсіздік ұғымы қаншалықты кең болса, олардың шығару әдістеріде соншалықты көп. Сондықтан қазіргі уақытқа дейінгі теңдеулер мен теңсіздіктердің дамуында әр түрлі әдістердің өзгеріп, жаңарып осы ұғымдардың нақтылануы мен басқада математикалық білімдермен байланысын ескеріп отыруды қажет етеді.
Алгебралық кеңінен баяндалатын сандар жүйелері мен функциялар, теңсіздіктер сол сияқты көптеген геометриялық тұжырымдарға байланысты мәселелер, проблемалар логикалық жағынан теңдеулер мен теңдеулер жүйелері мен тығыз байланысты болады. Олай болса, теңдеулер, теңсіздіктер және олардың жүйелерін аталған маңызды мәселелерден мүлде оқшау жалаң қарастыруға болмайды.
Теңдеу тарихы ерте замандағы математикамен тығыз байланысты.
Мысалы, координат әдісінің және аналитикалық геометрияның пайда болуымен дамуы теңдеулерді тек алгебрада сандар жүйесінде ғана қолданып қоймай әр түрлі геометриялық фигуралар жөніндегі есепке де қолдана бастады. Бұл бағыт алгебраның дамуына өз әсерін тигізді. Теңдеу алгебралық ұғым ретінде өзінің пайда болуы жөнінен негізгі үш бөлікке бөлінеді:
1. теңдеу мазмұнды есептер шешу құралы;
2. теңдеу алгебралық объектіні үйретуге қызмет ететін ерекше формуланың ролін атқарады;
3. теңдеу формула ретінде қосымша санды немесе өзінің шешімі болатын нүктенің координатасын анықтайды.
Сонымен, теңдеу көп аспектілі жалпы математикалық ұғым. Математикалық білім беру ісінде ешбір аспектіні қалдыруға болмайды.
Теңдеу тақырыбының маңыздылығы және ауқымының кеңдігіне байланысты оны осы заманда үйретудің мазмұнды - әдістемелік бағыты - теңдеу және теңдеулер жүйесі. Бұл арада теңдеулер мен теңдеулер жүйелері ұғымын қалыптастыру үшін оларды шешудің жалпы және дербес әдістері, мектеп математикасының курсында санды, функционалдық бағыттар бойынша теңдеулер мен теңдеулер жүйелерін, теңсіздіктерді үйренудің тығыз байланыстылығы қарастырылады.
Теңдеудің пайда болу обылысы және теңдеу ұғымының алгебрадағы атқаратын міндетіне сәйкес мектеп математикасындағы теңдеулер мен теңдеулер жүйелерін үш бағытқа бөлеміз:
А) Қолданбалы бағыт. Теңдеулер мен олардың жүйелерін мазмұнды есептерді шешуге қолдану. Математиканың басқа ғылымда қолданылуын оқытудағы әдістер мен тәсілдер көбінесе теңдеулерге сүйенеді.
Қазіргі математиканың басқа тарауларда қолданылуы көбінесе математикалық модельдеуге байланысты. Осы ұғымды пайдаланып теңдеулер мен олардың жүйелері математикалық модельдеудегі негізгі құрал ретінде аңықталады.
Б) Теңдеу мен теңдеулер жүйелерін үйренудегі теориялық - математикалық бағыт екі аспектіден тұрады:
1. аса маңызды теңдеулер және олардың жүйелерінің класын оқу;
2. бір бағытқа жататын жалпыланған ұғымдармен әдістерді бүтіндей үйрену. Осы екі аспекті де мектеп математикасында аса қажет.
Жалпыланған ұғымдар мен әдістерді қолдану теңдеулер мен олардың жүйелерін үйрену бағытын логикалық жағынан реттейді; олар бөлек класқа жататын есептерді шешудің жалпы тәсілдерін сипаттайды.
Өз кезегінде жалпы ұғымдар мен тәсілдер: белгісіз, теңдік, мәндестік, логикалық келіп шығу, сияқты теңдеу шешудегі негізгі логикалық ұғымдарға сүйенеді.
В) Теңдеулер мен олардың жүйелерін үйрену математикасының басқа тарауларымен байланысын орнату арқылы сипатталады.
Теңдеулер мен олардың жүйелері сан ұғымымен тығыз байланысты. Теңдеу арқылы сан жүйесін біртіндеп кеңейтуге болады. Мектеп алгебрасы мен анализ бастамаларындағы қарастырылатын барлық сандар, барлық нақты сандар теңдеу және теңсіздіктер, олардың жүйелерін шешумен тығыз байланысты. Мұндай байланыстың ең маңыздылығы функцияны зерттеуге теңдеудің қолданылуы (анықтау обылысын табу, таңба, олардың осы аралықтағы түбірлері т. б. ) . Сондықтан бұл айтылған мәселелер зерттеліп отырған тақырыптың өзектілігін анықтайды.
Зерттеу мақсаты - рационал және иррационал теңдеулер мен теңсіздіктер ұғымына анықтама бере отырып, оларды шешудің түрлі әдістерін жан-жақты зерттеу, оларды есеп шығаруда қолдана білу мәселелерін қарастыру.
Зерттеу пәні - рационал және иррационал теңдеулер мен теңсіздіктерді шешу әдістерінің математикалық шарттары.
Зерттеу нысаны - рационал және иррационал теңдеулер мен теңсіздіктерге берілген есептерді шешу барысында кездесетін мәселелерге әдістер қолдануға ықпалы.
Зерттеу болжамы -теңдеулер мен теңдеулер жүйелері оқушыларды еңбек сүйгіштікке тәрбиелейді. Қарастырылатын мәселерді ең тиімді, ұтымды, пайдалы жақтарынан зерттеуге үйретеді. Атқарылатын жұмыстарға терең, салыстырмалы түрде жан-жақты талдаулар жасай отырып, дұрыс жоспар құруға пәрменді көмегін тигізеді. Орындалған жұмыстардың нәтижелеріне сыншыл көзқараспен қорытындылар жасауға үйретеді. Оқушылардың ойлау жүйесінің, ой қорытындыларының ұтымды логикалық жолымен дамуына кең жол салады. Олай болса, теңдеулер мен теңдеулер жүйелері мектеп математикасын басқа салалары сияқты, оқушылардың ойлау жүйесінің жас жеткіншектерге лайықты дамуына, оларды қоғамға, Отанына пайдалы азамат болып қалыптасуына лайықты пайдасын тигізеді.
Курстық жұмыста рационал, иррационал өрнектер, теңдеулер, теңсіздіктер жайында негізгі түсініктер және де оларды шығару әдістері қарастырылды. Курстық жұмыс кіріспе, екі тараудан, бөлімдерден, қорытындыдан және пайдаланылған әдебиеттер тізімінен тұрады.
1РАЦИОНАЛ ЖӘНЕ ИРРАЦИОНАЛ ТЕҢДЕУЛЕР
1. 1 Рационал өрнек және оның қарапайым түрі
Кез келген көпмүшені бүтін өрнек деп атайды[1] . Екі бүтін өрнектің қатынасын рационал өрнек деп атаймыз:
 . (1. 1. 1)
. (1. 1. 1)
Мұндағы
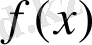 және
және
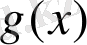 - берілген көпмүшелер. Бөлшек сандарға ұқсас, рационал өрнектерге де арифметикалық амалдар қолдануға болады:
- берілген көпмүшелер. Бөлшек сандарға ұқсас, рационал өрнектерге де арифметикалық амалдар қолдануға болады:

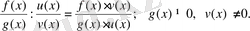
Егер рационал өрнектің алымы мен бөлімінің ортақ (комплекс) түбірлері болмаса, онда бұл өрнекті қысқартылмайтын бөлшек деп атайды. Рационал сандарға ұқсас, әрбір рационал өрнекті қысқармайтын бөлшек түрінде жазуға болады.
Егер рационал өрнектің алымының дәрежесі бөлімінің дәрежесінен кем болса, онда бұл өрнекті дұрыс бөлшек деп атаймыз. Мұнда нөлдік көпмүшені де дұрыс бөлшек ретінде қарастырамыз.
Теорема. 1. Әрбір рационал өрнек жалғыз ғана түрде бүтін өрнекпен (көпмүше) дұрыс бөлшектердің қосындысы түрінде жазылады. [1]
Дәлелдеуі:
Айталық,
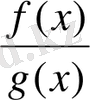 рационал өрнегі берілсін. Онда
рационал өрнегі берілсін. Онда
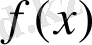 көпмүшесін
көпмүшесін
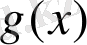 - ке қалдықпен бөлу арқылы
- ке қалдықпен бөлу арқылы
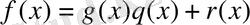 теңдігін аламыз. Мұнда
теңдігін аламыз. Мұнда
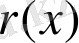 - тің дәрежесі
- тің дәрежесі
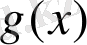 - тің дәрежесінен кем. Сонда
- тің дәрежесінен кем. Сонда
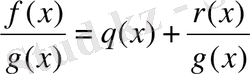 (1. 1. 2)
(1. 1. 2)
теңдігі шығады. Енді бұл теңдіктің жалғыздығын көрсетейік. Айталық,
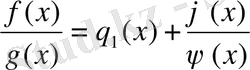 (1. 1. 3)
(1. 1. 3)
теңдігі де орындалсын. Мұнда
 - тің дәрежесі
- тің дәрежесі
 - тің дәрежесінен кем. Онда (1. 1. 2) және (1. 1. 3) теңдіктерден
- тің дәрежесінен кем. Онда (1. 1. 2) және (1. 1. 3) теңдіктерден
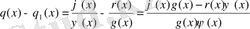 (1. 1. 4)
(1. 1. 4)
теңдігін аламыз. Оның оң жағында дұрыс бөлшек, ал сол жағында көпмүше орналасқандықтан,
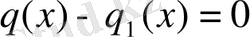 немесе
немесе
 болуы керек. Онда
болуы керек. Онда
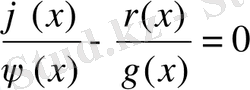 не
не
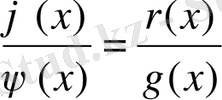 теңдіктері де орындалуы қажет. Теорема дәлелденді.
теңдіктері де орындалуы қажет. Теорема дәлелденді.
Рационал өрнектердің (1. 1. 2) түрде жазылуын оның қарапайым түрі деп атайды.
Анықтама. Бүтін рационал өрнек деп Н. Я. Виленкиннің оқулығы бойынша келесі түрдегі өрнек аталады:
(БРӨ) : = <сан> / <әріп>/ / <БРӨ> + <БРӨ> / / БРӨ/ <БРӨ>
Мысалы,
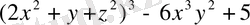 - бүтін рационал өрнек.
- бүтін рационал өрнек.
Екі бүтін рационал өрнектердің көбейтіндісі, қосындысы, айырмасы бүтін рационал өрнек болады.
Анықтама.
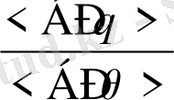 - өрнегі бөлшек - рационал өрнек немесе рационал өрнек болады.
- өрнегі бөлшек - рационал өрнек немесе рационал өрнек болады.
Анықтама.
 алгебралық өрнегі рационалды деп аталады, егер оған кіретін
алгебралық өрнегі рационалды деп аталады, егер оған кіретін
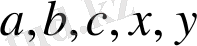 үшін қосу, көбейту, азайту, бөлу және бүтін дәреже алу амалдарынан басқа ешқандай амал орындалмаса.
үшін қосу, көбейту, азайту, бөлу және бүтін дәреже алу амалдарынан басқа ешқандай амал орындалмаса.
Мысалы,
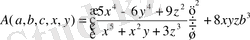 - бөлшек - рационалды өрнек.
- бөлшек - рационалды өрнек.
Егер бөлшек - рационалды өрнек берілсе, онда оның анықталу облысы (табылу облысы) өрнектің бөлімі нөлге тең болатындай айнымалылардың мәндерінен басқа барлық мәндерімен анықталады.
Мысалы,
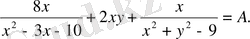
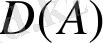 анықталу облысы:
анықталу облысы:
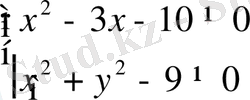
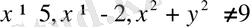
Координаттық жазықтыөта бұл шеңбер мен
 түзулердің нүктелерінен басқа барлық нүктелерді береді.
түзулердің нүктелерінен басқа барлық нүктелерді береді.
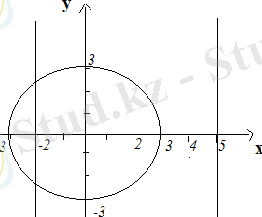
(1 - сурет)
Анықтама.
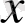 айнымалылы бүтін рационал өрнек деп
айнымалылы бүтін рационал өрнек деп
 , мұндағы
, мұндағы
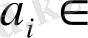 R
,
R
,
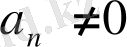 түріндегі өрнек аталады.
түріндегі өрнек аталады.
Теорема.
Егер
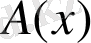 және
және
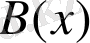 -
-
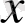 айнымалылы нақты коэффициентті көпмүшеліктер болса және
айнымалылы нақты коэффициентті көпмүшеліктер болса және
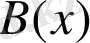 - нөлдік көпмүшелік болмаса, онда
- нөлдік көпмүшелік болмаса, онда
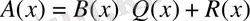 орындалатындай
орындалатындай
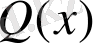 және
және
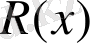 көпмүшеліктері табылады.
көпмүшеліктері табылады.
1. 2 Безу теоремасы. Көпмүшеліктердің түбірлері
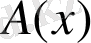 көпмүшелігін
көпмүшелігін
 екімүшелігіне бөлейік.
екімүшелігіне бөлейік.
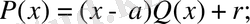 (
(
 - дәрежесі 1 болғандықтан, оның қалдығының дәрежесі 1 - кіші) .
- дәрежесі 1 болғандықтан, оның қалдығының дәрежесі 1 - кіші) .
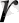 мәнін табу үшін
мәнін табу үшін
 деп алайық, сонда
деп алайық, сонда
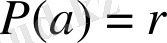 , яғни теореманы дәлелдедік.
, яғни теореманы дәлелдедік.
Теорема. 1 (Безу) .
Көпмүшелікті
 бөлгендегі қалдық
бөлгендегі қалдық
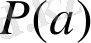 болады.
болады.
Жоғарыдағы теоремадан Безудің көпмүшеліктердің түбірлері туралы теоремасының дәлелдеуі шығады.
Теорема. 2 (Безу) .
Егер
 көпмүшелігінің түбірі бар болса, онда бұл көпмүшелік
көпмүшелігінің түбірі бар болса, онда бұл көпмүшелік
 көпмүшелігіне қалдықсыз бөлінеді.
көпмүшелігіне қалдықсыз бөлінеді.
 ,
,
 - түбір болғандықтан,
- түбір болғандықтан,
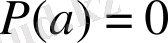 , ендеше
, ендеше
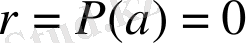 .
.
Анықтама.
Анықталу облыстары бос емес
 және
және
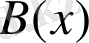 рационал өрнектері ортақ анықталу облыстарында теңбе - тең деп аталады, егер
рационал өрнектері ортақ анықталу облыстарында теңбе - тең деп аталады, егер
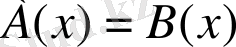 теңдігі ортақ анықталу облысында жататын барлық
теңдігі ортақ анықталу облысында жататын барлық
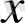 үшін орындалса.
үшін орындалса.
 рационал өрнегін өзіне теңбе - тең өрнекпен ауыстыру (ортақ анықталу облысында) - осы өрнекті теңбе - тең түрлендіру деп аталады.
рационал өрнегін өзіне теңбе - тең өрнекпен ауыстыру (ортақ анықталу облысында) - осы өрнекті теңбе - тең түрлендіру деп аталады.
Мысалы,
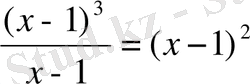 -
R
-
R
 жиынында теңбе - теңдік деп аталады.
жиынында теңбе - теңдік деп аталады.
Енді рационал өрнектердің тағы бір қасиетін қарастырайық. Нақты сандар өрісінде
 және
және
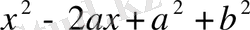 көпмүшелері ғана келірілмейтін көпмүшелер болатыны белгілі. Мұнда
көпмүшелері ғана келірілмейтін көпмүшелер болатыны белгілі. Мұнда
 және
және
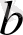 нақты сандар. Осыдан, егер
нақты сандар. Осыдан, егер
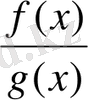 дұрыс бөлшектің бөлімі
дұрыс бөлшектің бөлімі
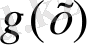 қандай да бір келтірілмейтін
қандай да бір келтірілмейтін
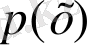 көпмүшесінің дәрежесіне тең болса және
көпмүшесінің дәрежесіне тең болса және
 - тің дәрежесі
- тің дәрежесі
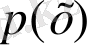 - тің дәрежесінен кем болса, онда бұл бөлшекті
жай бөлшек
деп атаймыз. Жоғары математика курсында мынадай маңызды теорема дәлеледенеді.
- тің дәрежесінен кем болса, онда бұл бөлшекті
жай бөлшек
деп атаймыз. Жоғары математика курсында мынадай маңызды теорема дәлеледенеді.
Теорема. 2. Әрбір дұрыс бөлшек жай бөлшектердің қосындысына бір ғана түрде жіктеледі. [1]
Бұл теореманы дәлелдеусіз қабылдаймыз. Дұрыс бөлшекті жай бөлшектердің қосындысына жіктеудің төмендегі анықталмаған коэффициенттер тәсілін мысап арқылы түсіндірейік.
Мысалы,
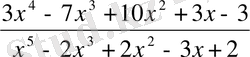 дұрыс бөлшегін жай бөлшектердің қосындысына жіктеу керек.
дұрыс бөлшегін жай бөлшектердің қосындысына жіктеу керек.
Шешуі:
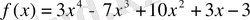 және
және
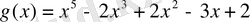 болсын. Онда
болсын. Онда
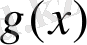 көпмүшесінің түбірлерін тауып, оны жай көбейткіштерге жіктелік:
көпмүшесінің түбірлерін тауып, оны жай көбейткіштерге жіктелік:
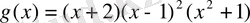 . Мұнда
. Мұнда
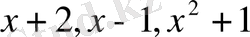 келтірілмейтін көпмүшелер болғандықтан,
келтірілмейтін көпмүшелер болғандықтан,
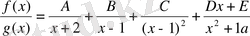 (1. 2. 1)
(1. 2. 1)
болатындай
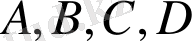 және
және
 сандары табылады. Мұнда
сандары табылады. Мұнда
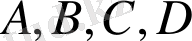 және
және
 - белгісіз коэффициенттер. Оларды (1. 2. 1) теңдік орындалатындай етіп, таңдап алу қажет. Ол үшін (1. 2. 1) теңдіктің оң жағын ортақ бөлімге келтіріп, шыққан бөлшектің алымын
- белгісіз коэффициенттер. Оларды (1. 2. 1) теңдік орындалатындай етіп, таңдап алу қажет. Ол үшін (1. 2. 1) теңдіктің оң жағын ортақ бөлімге келтіріп, шыққан бөлшектің алымын
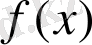 - ке теңестіреміз:
- ке теңестіреміз:

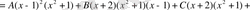
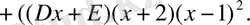
Бұл теңдіктің оң жақ бөлігін ықшамдап,


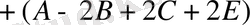
теңдігін аламыз. Осыдан
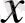 - тің бірдей дәрежелерінің алдындағы коэффициенттерін теңестіре отырып,
- тің бірдей дәрежелерінің алдындағы коэффициенттерін теңестіре отырып,
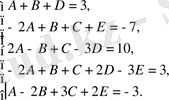
теңдеулер жүйесін аламыз. Оның шешіуі:
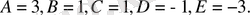 Сонда
Сонда

1. 3 Бөлшек - рационал теңдеулер
Математикада теңдік
 таңбасы өте жиі қолданылады. Бірақ оның мағынасы барлық жағдайда бірдей емес. Мысалға, теңдік белгісімен екі санды байланыстыруға болады.
таңбасы өте жиі қолданылады. Бірақ оның мағынасы барлық жағдайда бірдей емес. Мысалға, теңдік белгісімен екі санды байланыстыруға болады.
- ;
- ;
- ;
- .
Осындай жазулардың әрқайсысы ақиқат не жалған болатын пікірлерді береді. 1), 2), 3) - пікірлері ақиқат, ал 4) - пікірі жалған, - 10 болуы керек
Осындай пікірлердің ақиқат не жалғандығы анықтау үшін кейбір амалдар орындау қажет: бөлшектерді қосу, көбейткіштерге жіктеу, дәрежеге шығару, түбірден шығару және т. б. Бірақ, теңдіктің мағынасы сақталады: таңбаның сол жағы мен оң жағында бір сан тұрады. Осындай түрдегі пікірлерді сандық теңдіктер деп атайды (4 - ші пікір - дұрыс емес теңдік) . Теңдік таңбасы функциялардың теңдігі жөнінде айтқан кезде де қолданылады. Екі функция
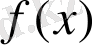 және
және
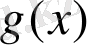 тең (беттесетін) деп аталады, егер:
тең (беттесетін) деп аталады, егер:
- Олардың анықталу облыстары беттесе:.
- үшін функциялардың мәндері беттесе, яғни.
Функциялардың теңдігі
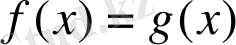 жазуымен көрсетіледі. Егер
жазуымен көрсетіледі. Егер
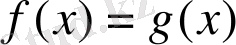 болса, онда
болса, онда
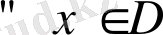 үшін функциялар бетеседі.
үшін функциялар бетеседі.
Мысалы,
- - теңбе - теңдік,
- - теңбе - теңдік;
- үшін, (немесе) .
Теңдік
 таңбасының мағынасы теңдеулерді қарасытырған кезде мүлдем басқа.
таңбасының мағынасы теңдеулерді қарасытырған кезде мүлдем басқа.
Анықтама.
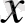 - ке тәуелді
- ке тәуелді
 және
және
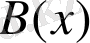 өрнектері үшін
өрнектері үшін
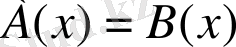 жазылуы
жазылуы
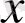 айнымалылы теңдеу деп аталады. Теңдеуге қойғанда дұрыс сандық теңдікке айналатын барлық
айнымалылы теңдеу деп аталады. Теңдеуге қойғанда дұрыс сандық теңдікке айналатын барлық
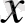 айнымалыларының жиыны теңдеудің шешімдер жиыны деп аталады, ал айнымалылардың теңдікке қанағаттандыратын әрбір осындай мәні теңдеудің түбірі деп аталады.
айнымалыларының жиыны теңдеудің шешімдер жиыны деп аталады, ал айнымалылардың теңдікке қанағаттандыратын әрбір осындай мәні теңдеудің түбірі деп аталады.
Анықтама.
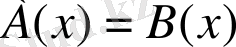 (немесе
(немесе
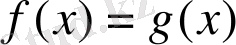 ) теңдеуін шешу дегеніміз оның түбірлерін табу немесе оның түбірлері болмайтынын дәлелдеу.
) теңдеуін шешу дегеніміз оның түбірлерін табу немесе оның түбірлері болмайтынын дәлелдеу.
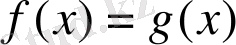 - бір жағдайда теңдеу, ал кейбір жағдайда тепе - теңдік болады.
- бір жағдайда теңдеу, ал кейбір жағдайда тепе - теңдік болады.
Мысалы,
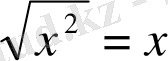
 болған кезде оны тепе - теңдік деп қарастыруға болады, ал егер теңдеу деп қарастырса, онда оның шешімі
болған кезде оны тепе - теңдік деп қарастыруға болады, ал егер теңдеу деп қарастырса, онда оның шешімі
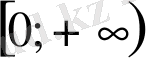 жиыны болады.
жиыны болады.
Теңдеудің шешімдер жиыны бос жиын да болуы мүмкін.
Мысалы,
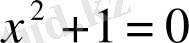 R
жиынында оның шешімдер жиыны бос жиын, ал
С
жиынында оның шешімдер жиыны
R
жиынында оның шешімдер жиыны бос жиын, ал
С
жиынында оның шешімдер жиыны
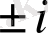 .
.
Теңдеулердің классификациясын белгісіздерге қолданылатын математикалық амалдар арқылы беруге болады.
Алгебралық теңдеулерде қосу, азайту, көбейту, бөлу бүтін дәрежеге алу, түбірден шығару амалдарын қолдануға болады.
Егер белгісіздерге иррационал дәрежеге алу, логарифмдеу, синусын, тангенсін табу және т. б. амалдар қолданса, ондай теңдеу транцендентті деп аталады.
Мысалы,
- - алгебралық теңдеу болады, себебі.
- - транцендентті теңдеу болады, себебі.
Алгебралық теңдеулердің жеке жағдайлары.
- Рационал теңдеулер, яғни айнымалысы бар өрнектен түбір алынбайтын теңдеулер.
Бөлшек - рационалтеңдеулер. Жеке жағдайы:
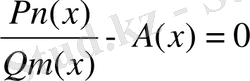
- Иррационал теңдеулер, яғни айнымалысы бар өрнектен түбір алу амалы орындалатын теңдеулер:.
Теңдеулерді шешу әдістері теңдеулердің мәндестігіне негізделеді.
Анықтама.
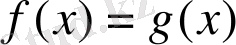 және
және
 екі теңдеу мәндес деп аталады, егер біреуінің шешімі екіншісінің шешімі болса, керісінше, егер екіншісінің шешімі біреуінің шешімі болса.
екі теңдеу мәндес деп аталады, егер біреуінің шешімі екіншісінің шешімі болса, керісінше, егер екіншісінің шешімі біреуінің шешімі болса.
Екі бірдей теңдеулердің мәндес болуы не болдмауы олардың қандай сандық жиында қарастырылуына байланысты анықталады.
Мысалы,
(1)
 және (2)
және (2)
 R
жиынында мәндес болады, нақты түбірі
R
жиынында мәндес болады, нақты түбірі
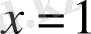 .
.
С
(комплекс сандар) жиынында мәндес болмайды, себебі (1) теңдеудің тағы
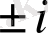 түбірлері бар.
түбірлері бар.
Түбірлері табылмайтын екі теңдеу мәндес болады.
Мысалы,
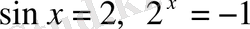 - мәндес теңдеулер, түбірлер жиыны Ø.
- мәндес теңдеулер, түбірлер жиыны Ø.
Сонымен қатар, берілген теңдеуді оған мәндес теңдеумен әрқашан ауыстыра беруге болмайды. Егер берілген теңдеуге қандайда бір түрлендіру жасайтын болсақ, түбірлерінің барлығы берілген теңдеудің түбірі болмайтын жаңа теңдеу алынуы мүмкін, яғни түрлендіру барысында артық түбірлер пайда болады.
Анықтама.
Кейбір (1. 1. 1)
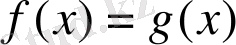 және (1. 1. 2)
және (1. 1. 2)
 теңдеулер берілсін. (1. 1. 2) теңдеуі (1. 1. 1) теңдеуінің салдары деп аталады, егер (1. 1. 1) теңдеуінен (1. 1. 2) теңдеуіне өту барысында оның түбірлері жоғалмаса, яғни (1) теңдеуінің барлық түбірлері (1. 1. 2) теңдеуінің түбірлері болса.
теңдеулер берілсін. (1. 1. 2) теңдеуі (1. 1. 1) теңдеуінің салдары деп аталады, егер (1. 1. 1) теңдеуінен (1. 1. 2) теңдеуіне өту барысында оның түбірлері жоғалмаса, яғни (1) теңдеуінің барлық түбірлері (1. 1. 2) теңдеуінің түбірлері болса.
Мысалы,
(1. 1. 1)
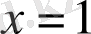 және (1. 1. 2)
және (1. 1. 2)
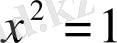 теңдеулері берілсін. Мұнда (1. 1. 2) теңдеуі (1. 1. 1) теңдеуінің салдары болады.
теңдеулері берілсін. Мұнда (1. 1. 2) теңдеуі (1. 1. 1) теңдеуінің салдары болады.
(1. 1. 1) және (1. 1. 2) теңдеулері мәндес болады, егер олардың әрқайсысы бір бірінің салдары болса.
Анықтама.
(1. 1. 1)
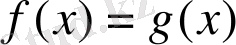 теңдеуі
теңдеуі
(1. 1. 3)

теңдеулер жиынына мәндес деп атаймыз, егер мына шарттар орындалса:
- (1. 1. 1) теңдеуінің әр түбірі (1. 1. 3) теңдеулерінің кем дегенде біреуінің түбірі болса;
- (1. 1. 3) жүйесіндегі теңдеулердің кез келген түбірі (1. 1. 1) теңдеуінің түбірі болса;
Яғни, егер
 - (1. 1. 1) теңдеуінің түбірлер жиыны болса, ал
- (1. 1. 1) теңдеуінің түбірлер жиыны болса, ал
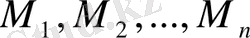 - сәйкесінше (1. 1. 3) теңдеулер жүйесіндегі теңдеулердің түбірлер жиындары болса, онда
- сәйкесінше (1. 1. 3) теңдеулер жүйесіндегі теңдеулердің түбірлер жиындары болса, онда
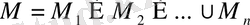 .
.
Олай болса, (1. 1. 1) теңдеудің түбірлерінің орнына (1. 1. 3) теңдеулер жүйесінің түбірлерін табуға болады.
Мысалы,
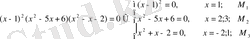
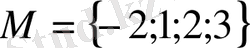 .
.
Теңдеуден теңдеулер жүйесіне өту барысында мынадай ережелерді сақтау керек:
- Жоғарыдағы әдіс өту кезінде түбірлердің жоғалуын болдырмайды, яғни егер(1) теңдеуінің түбірі болмаса, ондасанытеңдеулердің кем дегенде біреуінің түбірі болуы қажет.
- (1) теңдеуі үшінбарлық теңдеулерді шешіп, - түбірлер жиындарының бірігуін табу керек.
- Егер артық түбірлердің пайда болуында күмән туса, онда осы бірігуге кіретін әрбәр сан теңдеудің түбірі болатындығына тексерілуі керек.
1. 4 Түрлендіру әдістерімен теңдеулерді шешу әдістері
- Қосылғыштарды теңдеудің бір жағынан екінші жағына көшіру, яғнитеңдеудентеңдеуге көшкен кезде теңдеулердің мәндестігі сақталады.
- Ұқсас мүшелерін біріктіру, яғни(1. 1. 4)
- теңдеуден(1. 2. 1) теңдеуге көшкен кезде (1. 1. 4) теңдеуінің салдары болатын (*) теңдеуге келтіру.
Немесе
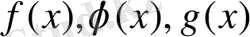 функциялары қандай болса да, (1. 2. 1) теңдеуі (1. 1. 4) теңдеуінің салдары болады, яғни теңдеудің артық түбірлері пайда болуы мүмкін, егер
функциялары қандай болса да, (1. 2. 1) теңдеуі (1. 1. 4) теңдеуінің салдары болады, яғни теңдеудің артық түбірлері пайда болуы мүмкін, егер
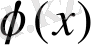 функциясы осы нүктелерде анықталмаса.
функциясы осы нүктелерде анықталмаса.
Немесе егер
 және
және
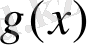 функцияларының анықталу облыстарының қиылысуы
функцияларының анықталу облыстарының қиылысуы
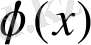 функциясының анықталу облысында жатса, яғни
функциясының анықталу облысында жатса, яғни
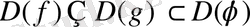 , онда (1. 1. 4) және (1. 2. 1) теңдеулері мәндес, яғни (1. 1. 4) ↔︎ (1. 2. 1) .
, онда (1. 1. 4) және (1. 2. 1) теңдеулері мәндес, яғни (1. 1. 4) ↔︎ (1. 2. 1) .
3. Теңдеудің екі жағын бір өрнекке көбейту, яғни
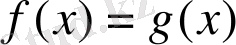 (1. 2. 1) теңдеуден
(1. 2. 1) теңдеуден
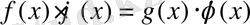 (1. 4. 1) теңдеуіне өту.
(1. 4. 1) теңдеуіне өту.
Сонымен, егер
 және
және
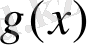 функциялары анықталатын әрбір нүктеде
функциялары анықталатын әрбір нүктеде
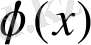 функциясы анықталса немесе
функциясы анықталса немесе
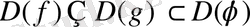 орындалса, онда (1. 4. 1) және (*) теңдеулері мәндес болады.
орындалса, онда (1. 4. 1) және (*) теңдеулері мәндес болады.
Ескеретін бір жағдай, (1. 2. 1) теңдеуінен (1. 4. 1) теңдеуіне келтіру кезінде, және керісінше, (1. 4. 1) теңдеуінен (1. 2. 1) теңдеуіне келтіру кезінде артық түбірлер пайда болуы мүмкін, сонымен бірге түбірлердің жоғалуы да мүмкін.
Мысалы,
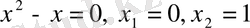 теңдеуін қарастырайық.
теңдеуін қарастырайық.
Екі жағын
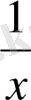 көбейтейік:
көбейтейік:
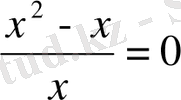 , ал бұл алғашқы теңдеудің салдары бола алмайды. Алғашқы теңдеудің түбірлері
, ал бұл алғашқы теңдеудің салдары бола алмайды. Алғашқы теңдеудің түбірлері
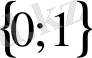 болса, түрлендіргеннен кейінгі теңдеудің түбірі
болса, түрлендіргеннен кейінгі теңдеудің түбірі
 .
.
Бұл жердегі түбірдің жоғалуы
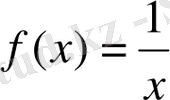 функциясының
функциясының
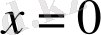 нүктесінде анықталмайтындығынан шығады.
нүктесінде анықталмайтындығынан шығады.
4.
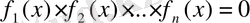 (1. 4. 2) теңдеуінен
(1. 4. 2) теңдеуінен
(1. 4. 3)

теңдеулер жүйесіне өтуге болады, егер өту кезінде олардың мәндестігі жоғалмайтын болса.
Теорема.
Егер
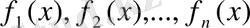 функциялары М жиынында анықталса (яғни М жиыны
функциялары М жиынында анықталса (яғни М жиыны
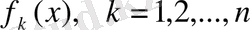 функцияларының әрқайсысының анықталу облысында жатса), онда осы жиында (1. 4. 2) теңдеуі мен (1. 4. 3) жүйесі мәндес болады.
функцияларының әрқайсысының анықталу облысында жатса), онда осы жиында (1. 4. 2) теңдеуі мен (1. 4. 3) жүйесі мәндес болады.
Шынымен, егер
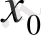 - (1. 4. 3) жүйесіндегі бір теңдеудің түбірі болса, онда
- (1. 4. 3) жүйесіндегі бір теңдеудің түбірі болса, онда
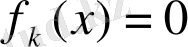 , ендеше
, ендеше
 және
және
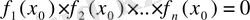 (себебі
(себебі
 ), бұдан
), бұдан
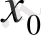 - (1. 4. 2) теңдеуінің түбірі. Керісінше, егер
- (1. 4. 2) теңдеуінің түбірі. Керісінше, егер
 (6) теңдеуінің түбірі болса, онда
(6) теңдеуінің түбірі болса, онда
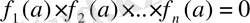 , себебі
, себебі
 нүктесінде барлық
нүктесінде барлық
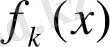 функциялары анықталған, сондықтан кем дегенде бір функция
функциялары анықталған, сондықтан кем дегенде бір функция
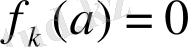 , ендеше
, ендеше
 саны (1. 4. 3) жүйедегі теңдеулердің кем дегенде біреуінің түбірі болады.
саны (1. 4. 3) жүйедегі теңдеулердің кем дегенде біреуінің түбірі болады.
Мысалы,
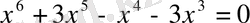 және
және
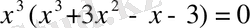 теңдеулері мәндес.
теңдеулері мәндес.
 теңдеуі
теңдеуі
 теңдеулер жүйесіне мәндес.
теңдеулер жүйесіне мәндес.
Ескерту.
Жалпы жағдайда
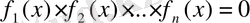 теңдеуі
теңдеуі
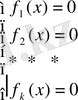 теңдеулер жүйесіне мәндес бола бермейді, себебі бұл функциялардың әрқайсысы
теңдеулер жүйесіне мәндес бола бермейді, себебі бұл функциялардың әрқайсысы
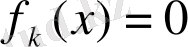 болатындай нүктеде анықталуыкерек.
болатындай нүктеде анықталуыкерек.
Мысалы,
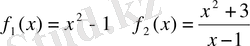
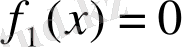 түбірлері
түбірлері
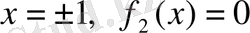 түбірлері жоқ. Ал
түбірлері жоқ. Ал
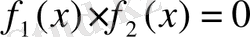 теңдеуінің бір ғана түбірі бар:
теңдеуінің бір ғана түбірі бар:
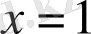 .
.
Теорема. (1. 4. 2) теңдеуінің әрбір түбірі (1. 4. 3) жүйесінің бір теңдеуінің түбірі боолады, яғни (1. 4. 3) теңдеулер жүйесі (1. 4. 2) теңдеуінің салдары болады.
5. Иррационал теңдеулерді шешу кезінде
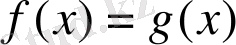 (1. 2. 1) теңдеуінен
(1. 2. 1) теңдеуінен
 теңдеуіне өту әдісі жиі қолданылады, және келесі түрде тұжырымдауға болады:
теңдеуіне өту әдісі жиі қолданылады, және келесі түрде тұжырымдауға болады:
- Кез келгенNүшінтеңдеуі (1. 2. 1) теңдеуінің салдары болады.
- Егер- тақ сан болса, онда теңдеулер М жиынында мәндес.
- Егер- жұп сан болса, ондатеңдеуі М жиынындатеңдеуіне мәндес, ал бұл теңдеу өз алдынатеңдеулер жүйесіне мәндес.
Мысалы,
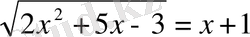
Екі жағынан квадраттаймыз:
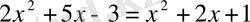 , бұл алғашқы теңдеудің салдары болып табылады.
, бұл алғашқы теңдеудің салдары болып табылады.
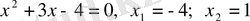
Тексеру барысында
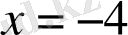 артық түбір екені анықталады, сонда жауабы
артық түбір екені анықталады, сонда жауабы

Берілген теңдеуді мына жүйемен ауыстыруға болады:
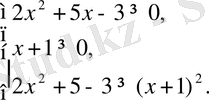
6. Айнымалыны ауыстыру әдісі - бұл әдіс
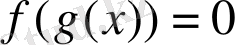 (1. 4. 4)
(1. 4. 4)
түріндегі теңдеулерді шешуде қолданылады.
Теорема.
(*)
 , мұнда
, мұнда
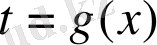 (
(
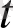 - көмекші белгісіз) теңдеуін қарастырайық және
- көмекші белгісіз) теңдеуін қарастырайық және
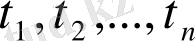 - (*) теңдеуінің түбірлері. Сонда (1. 4. 4) теңдеуін шешу үшін
- (*) теңдеуінің түбірлері. Сонда (1. 4. 4) теңдеуін шешу үшін
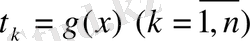 теңдеулердің әрқайсысның барлық түбірлерін тауып олардың шешімдер жиынын белгілесе жеткілікті, яғни:
теңдеулердің әрқайсысның барлық түбірлерін тауып олардың шешімдер жиынын белгілесе жеткілікті, яғни:
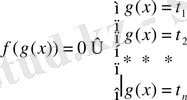
Мысалы,
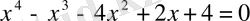 теңдеуін шешейік. Бұл қайтымды теңдеу.
теңдеуін шешейік. Бұл қайтымды теңдеу.
 (
(
 түбірі болмайды) бөлейік:
түбірі болмайды) бөлейік:
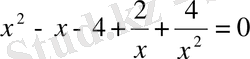 немесе
немесе
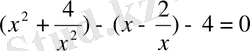 .
.
Белгісіз
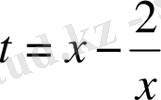 енгізейік, сонда
енгізейік, сонда
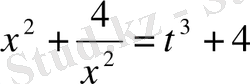 , яғни
, яғни
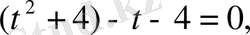
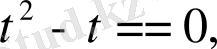
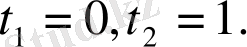 Сонда
Сонда
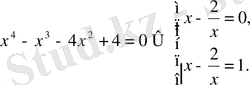
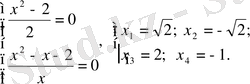
Жауабы:

1. 5 Бір айнымалылы бүтін рационал теңдеулер
Анықтама.
 және
және
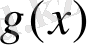 бүтін рационал өрнектердің
бүтін рационал өрнектердің
 теңдеуі бүтін рационал теңдеу деп аталады.
теңдеуі бүтін рационал теңдеу деп аталады.
Бұл теңдеудің мүмкін мәндер жиыны - R .
Мысалы,
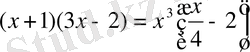 немесе
немесе
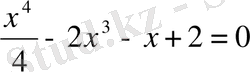 - төртінші дәрежелі бүтін рационал теңдеулер.
- төртінші дәрежелі бүтін рационал теңдеулер.
Анықтама.
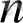 - дәрежелі бүтін рационал теңдеу деп
- дәрежелі бүтін рационал теңдеу деп
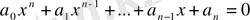 (1), мұндағы
(1), мұндағы
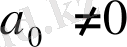 немесе
немесе
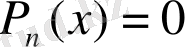 түріндегі теңдеу аталады.
түріндегі теңдеу аталады.
Егер
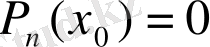 болса, онда
болса, онда
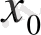 теңдеудің түбірі деп аталады.
теңдеудің түбірі деп аталады.
Алгебраның негізгі теоремасы. Сандар жиынында қарастырылған (1. 1. 1) түрдегі кез келген көпмүшеліктің кем дегенде бір түбірі табылады (алгебра курсынан)
Теорема. Комплекс сандар жиынында қарастырылған кез келген көпмүшеліктің түбірлер саны оның дәрежесіне тең.
Көпмүшеліктерді әрқашан сызықтық көбейткіштерге
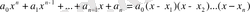 формуласымен жіктеуге болады, мұндағы
формуласымен жіктеуге болады, мұндағы
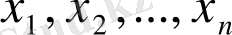 - көпмүшеліктің түбірлері, және олардың арасында тең болатындары да кездесуі мүмкін.
- көпмүшеліктің түбірлері, және олардың арасында тең болатындары да кездесуі мүмкін.
Шынымен де, алгебраның негізгі теоремасы бойынша
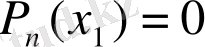 болатындай
болатындай
 , бірақ Безу теоремасы бойынша
, бірақ Безу теоремасы бойынша
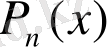 көпмүшелігі
көпмүшелігі
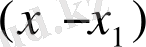 сызықтық көбейткішіне қалдықсыз бөлінуі керек, яғни
сызықтық көбейткішіне қалдықсыз бөлінуі керек, яғни
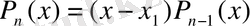 , сонымен бірге
, сонымен бірге
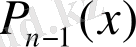 көпмүшелік болғандықтан:
көпмүшелік болғандықтан:
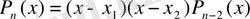 әне т. с. с. Сонымен
әне т. с. с. Сонымен
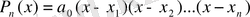 .
.
Виетт теоремасы. (көпмүшеліктің түбірлері мен коэффициентерінің арасындағы байланыс) .
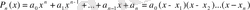 . (1. 5. 1)
. (1. 5. 1)
көпмүшелігі берілсін. Теңдеудің оң жағында екімүшелердің көбейтіндісін орындайық:

мұндағы:
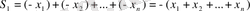 ,
,
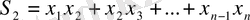 ,
,
* * *
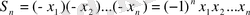 .
.
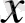 айнымалының бірдей дәрежедегі мүшелерінің коэффициенттерін салыстырайық:
айнымалының бірдей дәрежедегі мүшелерінің коэффициенттерін салыстырайық:

Егер
 екінші дәрежелі көпмүшелігі мен
екінші дәрежелі көпмүшелігі мен
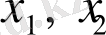 - оның түбірлері берілсе, онда:
- оның түбірлері берілсе, онда:

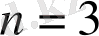 үшін көпмүшелік
үшін көпмүшелік
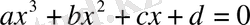 болады, және
болады, және
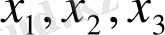 - көпмүшеліктің түбірлері болса, сонда:
- көпмүшеліктің түбірлері болса, сонда:
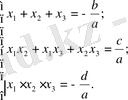
Теорема.
Егер
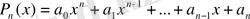 көпмүшеліктің барлық коэффициенттері бүтін сандар болса, онда
көпмүшеліктің барлық коэффициенттері бүтін сандар болса, онда
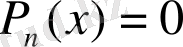 теңдеуінің кез келген бүтін түбірі
теңдеуінің кез келген бүтін түбірі
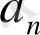 бос мүшенің бөлгіші болады.
бос мүшенің бөлгіші болады.
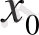 - көпмүшеліктің түбірі болсын, яғни
- көпмүшеліктің түбірі болсын, яғни
 , сонда
, сонда
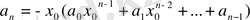 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz