Сызықтандырылған автоматты басқару жүйелерінің орнықтылығын Гурвиц, Михайлов және Найквист критерийлері арқылы зерттеу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. И. СӘТБАЕВ АТЫНДАҒЫ ҚАЗАҚ ҰЛТТЫҚ ТЕХНИКАЛЫҚ ЗЕРТТЕУ УНИВЕРСИТЕТІ
"Автоматтандыру және басқару" кафедрасы

МӨЖ №2
Тақырыбы: Автоматты басқару жүйелері. Орнықтылыққа зерттеу
Орындалған
%
Оқытушы: Орынбет М. М.
Магистрант: Аронова Ақбота Мамандығы: 6М072100
Алматы 2016
МАЗМҰНЫ
КІРІСПЕ
Жұмыс істеп тұрған автоматты жүйеге әртүрлі тұрақты сыртқы қозулар әсер етуі салдарынан реттелетін шығыстық шаманың мәні жиі өзгеріп отырады. Жүйенің автоматты реттеуіші осы реттелетін шаманы берілген мәнге келтіруге ұмтылады. Бірақ тұтастай алғанда жүйеде инерциялық массалар, реактивті элементтер (индуктивтік, сыйымдылық) болатындықтан, оның орнықты қалпына келуі, немесе қалыптасқан бір күйден келесісіне өтуі лезде емес, белгілі түрде кешігіп жүзеге асады. Жүйеде өтпелі процесс туындайды. Бұл жағдайда, егер жүйе қозу әрекеті тоқталғаннан кейін қалыптасқан күйге оралса, ол орнықты. Егер оралмаса, онда орнықсыз. Орнықсыз жұмыс кері байланыспен қамтылған АРЖ-ның барлығында туындауы ықтимал.
АРЖ-ның орнықтылығын анықтау мәселесі басты болып саналады, өйткені орнықсыз жүйелер іс жүзінде жарамсыз. Орнықтылықты зерттеудің жалпы әдісі АРЖ-ның g(t) жоспарлау (басқарушы) және f(t) қоздыру әсерлері тудыратын у(t) реттелетін шаманың өзгеруі үшін жазылған дифференциал теңдеуін талдаумен тұжырымдалады:
(а 0 р n + а 1 р n-1 + . . . +а n ) у(t) =(b 0 р m +b 1 р m-1 + . . . +b m ) g(t)
АРЖ-ның орнықтылығын әдетте орнықтылық критерийлерімен бағалайды. Орнықтылықтың негізгі Раус-Гурвиц, Михайлов және Найквист критерийлері секілді үш критерийі бар.
Бұл жұмыстың мақсаты - сызықтандырылған автоматты жүйелердің орнықтылығын талдау. Яғни, әртүрлі әдістер арқылы жүйені орнықталыққа зерттеу болып табылады.
1 Типтік сызықтық жүйелер
Әр түрлі реттеу жүйелерінің құрылымын бірлік математикалық аппарат көмегімен зерттеу үшін оларды құрылымдық сұлбалар түрінде көрсетеді. Мұндай жүйелер тармақтау түйіндерінен және динамикалық буындардан тұрады.
Тармақтау түйіндері. Мұндай түйіндерде кірістік сигнал өзінің мәнін өзгертпей бөлінеді де, бірнеше канал бойынша бағытталады.
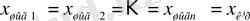
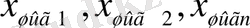 - тармақталу түйіндерінің шығыстық каналдарының сигналдары
- тармақталу түйіндерінің шығыстық каналдарының сигналдары
Қосу түйіндері. Мұндай түйіндерде кірістік сигнал
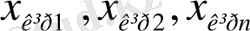 шығыста бір ғана сигнал тудырады.
шығыста бір ғана сигнал тудырады.
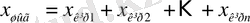
1. 1 Динамикалық буын
Мұндай буыннан өткен кірістік сигнал шығыста өзінің формасы мен шамасын өзгертеді.
Реттеу жүйелерінің физикалық сипаты жағынан әр түрлі өтпелі процестері динамикалық қасиеті жағынан ұқсас болып келеді. Сондықтан әрбір жүйе бір немесе бірнеше бірдей буындармен сипатталады. Көптеген буындардың әрекеті бір бағытты болып келеді (детектрлеушә қасиет) . Сигнал буыннан тек бір бағытта, яғни кірістен шығысқа өтеді, ал кері бағытта буын сигнал өткізбейді.
Жүйе буындары статикалық және астатикалық болады. Статикалық бында кірістік әсер тұрақты болғанда уақыттық шығыстық шама тұрақты мәнге қойылады, ал астатиалық буында қалыптасқан режимде шығыстық шама тұрақты жылдамдықпен немесе үдеумен үзіліссіз өзгереді.
Егер өтетін сигналдың өзгерісі алгебралық немесе 2-реттен жоғары емес дифференциалдық теңдеумен сипатталса ол типтік динамикалық бун деп аталады. Типтік буындарға: күшейтуші, интегралдаушы, дифференциалдаушы, апериодтық, тербелістік және кешігуші буындар жатады (1-кестені қараңыз) .
1-кесте - Типтік буындар түрлері
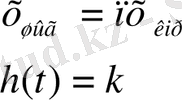
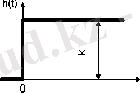
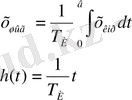

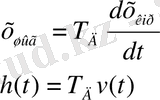
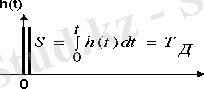
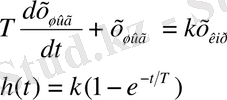
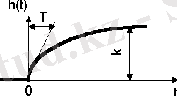
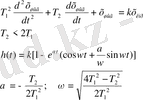
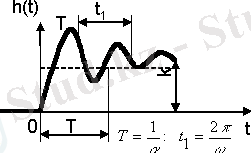
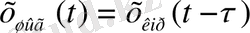
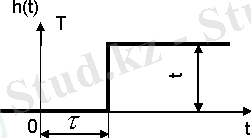
1. 2 Жиіліктік сипаттамалар
Жалпы жағдайда бір кірісті сызықты стационарлы жүйенің теңдеуін былай жазуға болады:
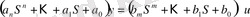 (1)
(1)
Анықтама бойынша оның беріліс функциясы:
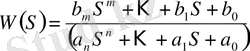 (2)
(2)
(2) теңдеудегі
 деп белгілейміз
деп белгілейміз
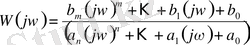
 - жиіліктік беріліс функция (ЖБФ)
- жиіліктік беріліс функция (ЖБФ)
ЖБФ жиіліктік деп аталатын нақты айнымалыға байланысты комплекстік - мәнді функция болып табылады.
 - функциясын келесі түрде көрсетуге болады:
- функциясын келесі түрде көрсетуге болады:
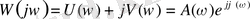 (3)
(3)
мұндағы:
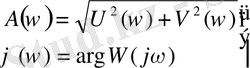 (4)
(4)
Егер
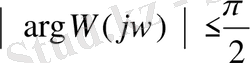 , онда
, онда
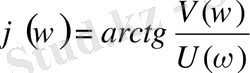 (5)
(5)
ЖБФ-ң нақты бөлігі
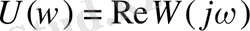 - нақты жиіліктік функция (НЖФ) .
- нақты жиіліктік функция (НЖФ) .
ЖБФ-ң жорамал бөлігі
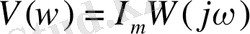 - жорамал жиілікті функция (ЖЖФ) .
- жорамал жиілікті функция (ЖЖФ) .
Жиілік
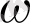 0-ден
0-ден
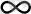 -ке дейін өзгергенде комплекстік жазықтықтағы жиіліктік беріліс функциясының векторының соңын білдіретін қисық амплитудалық-фазалық жиіліктік сипаттама (АФЖС) деп аталады.
-ке дейін өзгергенде комплекстік жазықтықтағы жиіліктік беріліс функциясының векторының соңын білдіретін қисық амплитудалық-фазалық жиіліктік сипаттама (АФЖС) деп аталады.
Нақты жиіліктік функцияның графигі
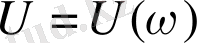 - бұл нақты жиіліктік сипаттама (НЖС) .
- бұл нақты жиіліктік сипаттама (НЖС) .
Жорамал жиіліктік фунцияның графигі
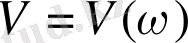 -бұл жорамал жиіліктік сипаттама(ЖЖС) .
-бұл жорамал жиіліктік сипаттама(ЖЖС) .
Жиіліктік беріліс функциясының модулі
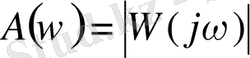 - бұл амплитудалық жиіліктік функция, ал оның графигі - фазалық жиіліктік сипаттама (ФЖС) .
- бұл амплитудалық жиіліктік функция, ал оның графигі - фазалық жиіліктік сипаттама (ФЖС) .
Тербеліс жиілігі
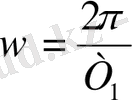 , фазалық жылжу
, фазалық жылжу
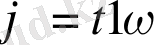 АЖС
АЖС
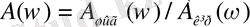
Жоғарыда айтылған жиіліктік сипаттамалаордан басқа логарифмдік жиіліктік сипаттамалар қолданылады (ЛЖС) .
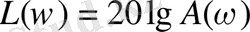 функциясы - логарифмдік амплитудалық жиіліктік функция (ЛАЖФ) . ЛАЖФ-ның жиілік логарифміне
функциясы - логарифмдік амплитудалық жиіліктік функция (ЛАЖФ) . ЛАЖФ-ның жиілік логарифміне
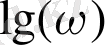 тәуелділік графигі логарифмдік фазалық жиіліктік сипаттама (ЛФЖС) деп аталады.
тәуелділік графигі логарифмдік фазалық жиіліктік сипаттама (ЛФЖС) деп аталады.
Фазалық жиіліктік функцияның
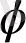 жиілік логарифміне
жиілік логарифміне
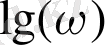 тәуелділік графигі логарифмдік фазалық жиіліктік сипаттама (ЛФЖС) деп аталады.
тәуелділік графигі логарифмдік фазалық жиіліктік сипаттама (ЛФЖС) деп аталады.
ЛАЖС және ЛФЖС-ны тұрғызғанда абцисса өсіне немесе
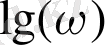 мәне, немесе жиіліктің өз мәні енгізіледі.
мәне, немесе жиіліктің өз мәні енгізіледі.
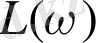 өлшем бірлігі -децибел (бел - сигнал қуатының күшейту коэффициентінің ондық логарифмінің өлшем бірлігі, яғни 1 бел қуатты 10 есе күшейтуді, 2 бел- 100 есені және т. с. с көрсетеді) .
өлшем бірлігі -децибел (бел - сигнал қуатының күшейту коэффициентінің ондық логарифмінің өлшем бірлігі, яғни 1 бел қуатты 10 есе күшейтуді, 2 бел- 100 есені және т. с. с көрсетеді) .
Ұзындық буындардың динамикалық қасиеттері және автоматты басқару жүйелерінің бүтінде дифференциалды теңдеулермен және қолдан-колға берілетын функциялармен суреттелген бола алады, сонымен қатар уақытша және жиі сипаттамалар арқасында . Уақыттардың функциясын, буын суреттеуші шығатын сигналы өзімен уақытша сипаттама ұсынады ( немесе жүйенің ) айқын буын кіруіне беру жанында сигнал тестіленген. Буын шығуында орналастырылған амалсыз тербелулерді бейнелеп түсіндіреді үндескен әсермен шақырылғандар кіруде.
Буын теңдеуімен тәжірибелік алынғана алады немесе салған болу . Болады және кері мүмкіншілік - тәжірибелік алынған сипаттамаларға буын теңдеуі біріктіру . Сонымен қатар, арқасында бұларды сипаттамаларды өз бетімен түр - ашу кернеуін буын реакциясын анықтауға болады . Өтетіндер
Және қолдан-колға берілетын функциямен буын дифференциалды теңдеуімен және оның бір мағыналы байлаулы және сонымен қатарға олардын буын динамикалық қасиеттерінің жеткілікті суреттеуімен келеді .
1. 3 Автоматты басқару жүйелерінің орнықтылығы
1. 3. 1 Сызықты АБЖ орнықтылық анализі
1. 3. 1. 1 Сызықты жүйелердің орнықтылық ұғымы
АБЖ-ң маңызды сипаттамаларының бірі - оның орнықтылығы. АБЖ орнықтылығы - бұл жүйені тұрақты жағдайдан шығарған әсер аяқталғаннан кейін қайтадан тұрақты, теңбе-тең жағдайға қайтадан оралуы. Тұрақты емес АБЖ тұрақты жағдайға қайтып келмей, одан алыстай береді.
АБЖ-ң орнықтылығынан оның жұмыс қабілеттілігі тәуелді болады. Әдеттте, орнықтылық ұғымы келесі мысалдармен түсіндіріледі. Жүйе ретінде, келесі үш жағдайда бола алатын шарды аламыз.
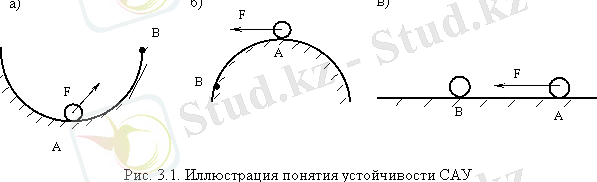
1) егер шар шұңғыл беттікте болса (а сурет), онда күштің әсерінен ол тыныштық жағдайдан шығады, бірақ сыртқы күш әсері таусылған соң қайтадан тұрақты жағдайға қайтып оралады. Бұл тұрақты жағдай.
2) егер шар дөңес беттікте болса, онда күштің әсерінен ол тыныштық жағдайдан шығады және сыртқы күш әсері таусылған соң да қайтадан тұрақты жағдайға қайтып орала алмайды. Бұл тұрақсыз жағдай.
3) егер шар тегіс беттікте болса, оған сыртқы күш әсер еткенде тұрақты жағдайдан шығып, сыртқы әсер таусылғаннан кейін қайтадан жаңа тұрақты жағдайға келеді. Мұндй жағдай нейтралды-тұрақты болып табылады.
1. 3. 1. 2 Орнықтылықтың алгебралық критерийі
(Гурвиц критериінің аналогы)
Зерттелетін тұйық импульстік жүйенің сипаттамалық теңдеуі:
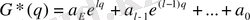
Сипатталық көпмүшеде G*(q) айнымалыларды ауыстырамыз:
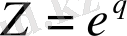
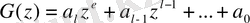
Осыған байланысты орнықтылықтың қажетті және жеткілікті шарты келесі түрде болады:
Егер G(z) = тің барлық түрірлері шеңбердің бірлік радиусының ішінде жатса, онда тұйық импульстік жүйе тұрақты, яғни G(z) барлық нөлдер модуль бойынша бірден аз болады.
Импульстік жүйенің орнықтылық шартын үзіліссіз жүйелер үшін Гурвицтің орнықтылық шартына келтіру үшін, көпмүшеге ауыстыру енгіземіз :
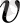 = ( z=1) /(z+1) немесе Z=(1+V) /(1-V)
= ( z=1) /(z+1) немесе Z=(1+V) /(1-V)
Онда
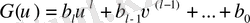
Онда импульстік жүйенің орнықтылық шарты келесі түрде: Егер түрлері сол жартылай жазықтықта жатса, онда тұйық импульстік жүйе тұрақты болады, яғни Гурвиц шарты орындалады:
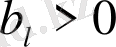 , Δ
, Δ
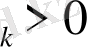 ,
,
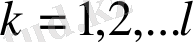
Δ
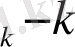 -ретті Гурвиц анықтауышы.
-ретті Гурвиц анықтауышы.
1. 3. 1. 3 Орнықтылықтың жиіліктік критериі
(Найквисттің критериінің анологы)
Егер ашық импульстік жүйе тұрақты болып, тұйық импульстік реттеу жүйесі тұрақты болады. Егер ашық жүйенің жиіліктік сипаттамасының годографы
 0-ден
0-ден
 -ге дейін өзгергенде (-1, j
-ге дейін өзгергенде (-1, j
 ) нүктесіне жетпесе.
) нүктесіне жетпесе.
Егер ашық импульстік жүйе тұрақты болмаса, яғни сызықты бөлімнің беріліс функциясы оң нақты бөлікті полюске ие болса және егер ашық жүйенің жиіліктік сипаттамасының годографы оң бағытта r/2 рет (-1; j0) нүктесіне жетсе тұйық импульстік ретсіз жүйесі тұрақты болады.
Егер ашық жүйе нейтралды болса, яғни беріліс функциясы нөлге тең r полюстерден тұрса және егер годограф - r
 /2 бұрышына сәйкес келетін доғамен толтырылса, онда импульстік жүйе тұрақты болады.
/2 бұрышына сәйкес келетін доғамен толтырылса, онда импульстік жүйе тұрақты болады.
1. 3. 2 Амплитудалық - импульстік модуляциялы жүйелердің сапасын зерттеу
АБЖ-рінің сапасын зерттегенде үш мәселе туады:
1) жүйенің қателік сигналының мәнін бағалау;
2) түсіру моментінің өтпелі процесінің қисығын тұрғызу;
3) өтпелі процесс параметрлерін жанама бағалау, біріншіден қайта реттеуді және реттеу уақытын бағалау.
Импульстік элементтің кірісіндегі сигнал:
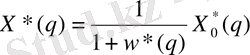
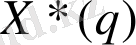 - жүйенің кірістік сигналы амплитудалық - импульстік модуляциялы жүйелерде реттеу процесінің сапа көрсеткіштерінің жанама бағалары : орнықтылық дәрежесі, тербеліс дәрежесі және интегралды қателіктер.
- жүйенің кірістік сигналы амплитудалық - импульстік модуляциялы жүйелерде реттеу процесінің сапа көрсеткіштерінің жанама бағалары : орнықтылық дәрежесі, тербеліс дәрежесі және интегралды қателіктер.
Орнықтылық дәрежесі - ξ тұйық жүйенің G*(q) =0 сипаттамалық теңдеуінің түбірінің минималды нақты бөлігі. ξ =min /
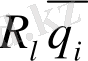 /. Орнықтылық дәрежесі - салыстырмалы шама. Орнықтылық дәрежесінің абсолютті шамасы ξ
/. Орнықтылық дәрежесі - салыстырмалы шама. Орнықтылық дәрежесінің абсолютті шамасы ξ
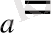 ξ /T.
ξ /T.
Тербеліс дәрежесі
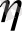 деп сипаттамалық теңдеудің түбірінің осьіне жақын, жорамал бөліктің нақты бөлікке қатынасының абсолютті шамасын айтады, яғни
деп сипаттамалық теңдеудің түбірінің осьіне жақын, жорамал бөліктің нақты бөлікке қатынасының абсолютті шамасын айтады, яғни
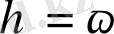 /ξ .
/ξ .
1. 4 Автоматты басқарудың сандық жүйелерінің динамикасын зерттеу
Сандық есептеу машиналары және әр түлі сандық есептегіш құралдар автоматты басқару жүйелерінде кең таралған. СЕМ-ры автоматты жүйелерде басқару процестерінің жоғары сапалық көрсеткіштерін алуға қолданылады. Сандық жүйелер динамикалық жағынан алғанда сигналды уақыт және деңгей бойынша кванттайды. Мұндай жүйелерге сигналды импульстік - кодтық модуляциялау тән.
Ү/Д - үзіліссіз сигналды дискреттіге түрлендіргіш;
Ү/Д түлендіргіш - деңгей бойынша квантталған көп сатылы элементтердің тізбекті қосылысы түрінде және амплитудалық - импульстік модуляциялы жүргізуші импульстік элемент ретінде болады.
Д/Ү - дикреттік сигналды үзіліссізге түрлендіргіш. Ол беріліс функциялы нөлдік қатарлы фиксатор болып табылтын қалыптастырғыш құрылғы түрінде болады. Сандық жүйелерді және амплитудалық - импульстік модуляциялы жүйелерді зерттегенде логарифмдік жиіліктік сипаттамаларды қолданамыз.
Логарифмдік жиіліктік сипаттамалар тәсілі
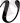 - түрлендіру негізіндежасалады.
- түрлендіру негізіндежасалады.
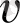 - түрлендіру келесі түрде:
- түрлендіру келесі түрде:
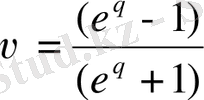 ;
;
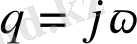 , деп белгілеп
, деп белгілеп
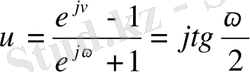
Теңдіктің оң бөлігі - жорамал шама болса, сол бөлігіде жорамал шама болады.
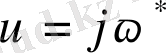 белгілеуін енгізіп
белгілеуін енгізіп
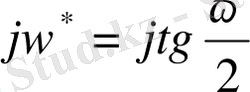 осыдан
осыдан
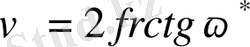
 шамасы 0- ден
шамасы 0- ден
 -ге өзгергенде
-ге өзгергенде
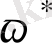 0-ден
0-ден
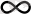 -ке өзгереді.
-ке өзгереді.
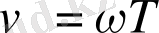 болған- дықтан :
болған- дықтан :
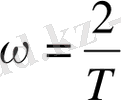 arctg
arctg
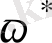
 шамасы 0-ден
шамасы 0-ден
 -ге өзгергенде
-ге өзгергенде
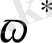 0-ден
0-ден
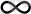 -ке өзгереді.
-ке өзгереді.
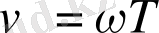 болған - дықтан :
болған - дықтан :
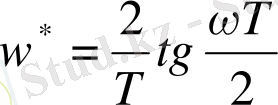
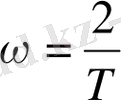 arctg
arctg
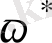
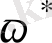 айнымалысы өлшемсіз жалған жиілік деп аталады.
айнымалысы өлшемсіз жалған жиілік деп аталады.
Ал өлшемді жалған жиілік
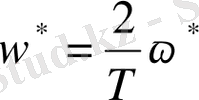 ,
,
яғни
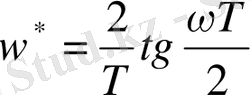 ;
;
Ашық сандық жүйенің динамика теңдеуі:
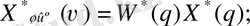
Егер бұл теңдеуге q айнымалысының орнына
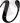 айнымалысын енгізсек,
айнымалысын енгізсек,
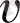 түрлендіру арқылы жағынан ашық сандық жүйенің динамика теңдеуді келесі түрге болады:
түрлендіру арқылы жағынан ашық сандық жүйенің динамика теңдеуді келесі түрге болады:
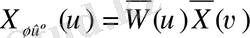 ;
;
Ашық сандық жүйенің жиіліктік сипаттамасына сәйкес келетін ЛЖС:
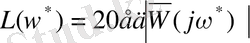 :
:
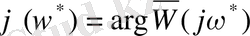 :
:
Уақыт және деңгей бойынша квантталған сандық автоматтық жүйелер сызықты емес импульстік жүйеге жатады. Абсолюттік орнықтылықты зерттеу үшін Цыпкин критериі қолданылады: Келтірілген үздіксіз бөлігі тұрақты және сызықты емес сипаттамасы (0, 1) секторында жатқан сызықты емес импульстік жүйенің тепе-теңдік жағдайы. Егер барлық жиіліктер диапазонында
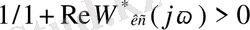 теңсіздігі орындалса, онда абсолютті тұрақты болады. Егер келтірілген сызықты бөлім тұрақты болмаса, абсолюттік орнықтылықтың жеткілікті критериі орындалмайды.
теңсіздігі орындалса, онда абсолютті тұрақты болады. Егер келтірілген сызықты бөлім тұрақты болмаса, абсолюттік орнықтылықтың жеткілікті критериі орындалмайды.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz