Сызықтық бағдарламалау: негізгі түсініктері, шешу әдістері және Крамер ережесін Excel-де қолдану


Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:
Мазмұны
Кіріспе3
1 Сызықтық бағдарламалау4
1. 1 Сызықтық бағдарламалау есебінің негізгі түсініктері4
1. 2 Сызықты бағдарламалау есебінің шешімін графикалық түрде табу6
1. 3 Крамер ережесі. Кері матрица әдісі. Гаусс әдісімен шығару8
2 Excel бағдарламасында Крамер ережесімен есеп шығару12
Қорытынды14
Пайдаланылған әдебиеттер15
КіріспеСоңғы жылдары халық шаруашылығын тиімді басқаруда математикалық әдістер мен есептеуіш техникалар жиі қолданылуда, Есептеуіш техникаларды дұрыс пайдалану үшін экономиканың әртүрлі саласында болатын заңдар мен құбылыстардың ағымын біліп қана қою жеткіліксіз. Ол үшін шаруашылықты басқаруға қажетті барлық ақпараттар мен мәліметтерді белгілі бір математикалық өрнектер түрінде бейнелеу қажет.
Зерттегелі отырған экономикалық процесті немесе құбылысты белгілі бір математикалық өрнектер түрінде бейнелеу дегеніміз - сол процестің немесе құбылыстың математикалық моделін құру деген сөз. Модель құру үшін экономикалық құбылыстар мен процестер белгілі бір дәрежеде абстракцияланады. Математикалық моделін құру барысында шаруашылықта болатын құбылыстар мен процестердің ең басты қасиеттері іріктелініп, математикалық өрнектер түрінде бейнеленеді.
1 Сызықтық бағдарламалау 1. 1 Сызықтық бағдарламалау есебінің негізгі түсініктеріСызықтық бағдарламалау есебі деп - бірнеше айнымалының сызықты функциясына, ол айнымалыларға қойылған сызықты шектеулер жағдайында функцияның экстремумын (max немесе min) іздеу есебі ұғылады. Мысалы: Берілген f ( x 1 , x 2 ) =2 x 1 +5 x 2 функциясының максимум мәнін, 1 с және 2 с айнымалыларына қойылған келесі шектеулерден табу керек:
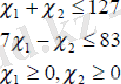
келтірілген сызықты бағдарламалау есебі екі айнымалының теңсіздік-шектеулермен берілген максимумдеу есебі. Теңсіздік шектеулер орнында теңдік-шектеулер де болуы мүмкін.
Сызықты f -функциясы мақсат функциясы, немесе мақсатты функция деп аталады.
Шектеулер x 1 ≥0, x 2 ≥0 теріс еместік шектеулері (немесе теріс еместік шарттары), ал сызықты теңсіздіктер және теңдеулер жүйесі сызықты бағдарламалау есебінің шектеулер жүйесі деп аталады.
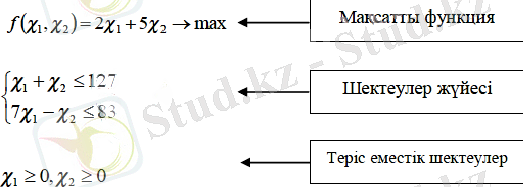
Сызықты бағдарламалау есебі көптен экономикалық есептер (өндірісті жоспарлау, ресурстарды пайдалану, көлікпен тасымалдау және т. б. ) үшін ыңғайлы математикалық үлгі болып табылады. Бірқатар экономикалық есептер үшін математикалық үлгілер құру процесін мысалдармен қарастырайық. Олар максимум мен минимумге берілген сызықты бағдарламалау есебі түрінде келтіріледі. Осы жерде өткен дәрісте келтірілген үлгі және математикалық үлгілеу (моделдеу) түсініктерін еске түсіруге болады. Үлгі - бұл түп нұсқаны ауыстыратын және оның зерттеуге қатысты маңызды сипаттары мен қасиеттерін бейнелейтін объект. Әрі қарай:
Математикалық қатынастардың жиынтығын көрсететін үлгі математикалық деп аталады. Біз оқитын пәнді математикалық экономиканың бір тармағы деп қарастыруға болады. Ал, математикалық экономика нақты экономикалық объектілердің математикалық үлгілерін зерттейді.
Келесі түсінік: Математикалық экономиканың әдісі - бұл экономиканы күрделі серпімді жүйе ретінде жүйелік талдау. Басқаша айтқанда өткен дәрісте қарастырылған талдау түсінігінің қажеттілігіне келеміз.
Жүйе - өзара байланыстағы белгілі бір мақсатты жүзеге асыратын элементтер бірлестігі. Олар экономикадан тыс болуы немесе ішкі жүйелер болуы мүмкін. Экономикада кездесетін есептерде әсіресе өндірісті жоспарлауға байланысты есептерде ең тиімді вариантты іздейтін экстремалды есептер қарастырылады. Мұндай есептерле параметрлер саны көп болуы нәтижесінде есептеулер жүргізу қиындыққа түседі. Сондықтанда әртүрлі математикалық әдістер ізделіп, есептеу машинасын пайдалану мүмкіндіктері қарастырылады.
Экономиканы математикалық модельдеудің үш негізгі этаптарын атап өтуге болады:
- Зерттеулердің мақсаты анықталып есептердің қойылымы анықталады және де объектіні сапа жағынан экономикалық модель ретінде сипаттау жүргізіледі.
- Зерттелетін объектінің математикалық моделі қалыптасады, алғашқы ақпараттар дайындалады.
- Математикалық модельге талдау жүргізіледі, алынған нәтижелер өңделіп талданады.
ЭЕМ қолдау көптеген жоспарлардың варианттарын салыстырып басқаруға қатысты шешімдер таңдауға мүмкіндік береді.
Экономикаға қатысты математикалық үлгілердің жай мысалдарына тоқталайық.
1. 2 Сызықты бағдарламалау есебінің шешімін графикалық түрде табуСызықты бағдарламалау есебінің шешімін графикалық түрде мынадай жағдайда іздеген қолайлы:
- Екі айнымалы пайдаланылған есептерде, егер шектеулер теңсіздік арқылы берілсе;
- Егер айнымалының саны көп болып, бірақ конондық жазылуында бос айнымалылар саны екіден аспаса.
Екі айнымалының сызықтық бағдарламалау есебінің қойылуы мынадай:
- Мақсатты функция Zmax=c1x1+x2x2(1)
- Шектеулер
 (2)
(2)
- - теріс еместік шарты x1≥0, x2≥0 -теріс (3)
(2) және (3) - ші теңсіздіктерінің әрқайсысы геометриялық тұрғыдан шеткі сызықтары
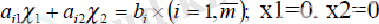
- болатын жартылай жазықтықтарды анықтайды.
Егер (2) - (3) теңсіздіктер жүйесі біріккен болса, оның шешімдерінің облысы барлық жартылай жазықтарға ортақ нүктелердің жиыны болады.
Аталған жартылай жазықтардың қиылысатын нүктелерінің жиыны дөңес болғандықтан, мүмкін шешімдер облысы дөңес жиын болады, оны шешімдер көпбұрышы деп атайды. Ол көпбұрыштың қабырғалары шектеулер жүйесіндегі теңсіздіктер орнына, теңдеулер алғаннан шыққан түзулер арқылы беріледі.
Сонымен (2) - (3) теңсіздіктердің мүмкін шешімдері облысы:
- Дөңес көпбұрыш;
- Шектеусіз дөңес көпбұрышты облыс;
- Құр облыс;
- Сәуле;
- Кесінді;
- Бірғана нүкте - болулары мүмкін.
(1) -ші мақсатты функция жазықтықта өзара параллель түзулердің бірлестігін анықтап олардың әр қайсысына z-тің белгілі бір мәні сәйкес болады.
C 1 , C 2 координаталарымен берілген C( C 1 , C 2 ) векторы z-тің ең жылдам өсу бағытын көрсетеді және жоғарыда аталған түзілерге перпендикуляр болады.
Егер белгілі бір координаттар жүйесінде (2) -(3) теңсіздіктер жүйесінің мүмкін шешімдері облысын және(1) параллель түзулер бірлестігін бір жерде кесіндесек, онда z функциясының максимумделуін анықтау есебі z-тің ең үлкен мәніне сәйкес болатын және ол арқылы z=const бірлестігінің түзуі өтетін мүмкін облысының нақты бір нүктесін табуға келеді. Мұндай шешімдердің облысы не шешімдердің көп бұрышы құр болмағанда және мақсатты функция жоғарыдан шенелген кезде бар болады. Ол шарттар орындалған кезде шешімдер көпбұрышының төбелерінің бірінде мақсатты функция ең үлкен мән қабылдайды. Бұл төбені анықтау үшін Z= C 1 * x 1 + C 2 * x 2 =0 бас нүкте арқылы өтетін және C=( C 1 ; C 2 ) векторына перпендикуляр болатын деңгейлер сызығын құрамызда, оны C=( C 1 ; C 2 ) векторынынң бағытында, шешімдер көпбұрышының ең шеткі нүктесімен құрылысқанша жылжыта береміз. Осы нүктенің координаторлары қойылған есепің тиімді жоспарын анықтайды.
Сызықтық бағдарламалау есебінің шешімдерін практикалық тұрғыда геометриялық жолмен былай ізедейді:
- (2) -(3) шектеулерде теңсіздіктер орнына теңдік белгілерін алып, олар анықталатын сызықтарды құру керек.
- Әрбір шектеулер анықтайтын жартылай жазықтықты табу керек.
- Шешімдер көпбұрышын табу керек.
- C=(C1; C2) векторын құру керек.
- C векторына перпендикуляр және бас нүкте арқылы Z=C1*x1+C2*x2=0 векторын құру керек.
- Z түзуін c векторы бағытымен жылжыту арқылы не мақсатты функция максимумделетін мән қабылдайтын нүктелер анықталады, не функцияның жоғарыдан шектелмегендігіне көз жеткізіледі.
- Функцияның максимум нүктелерінің координаталары анықталады да, не сол нүктедегі мақсатты функцияның мәні есептеледі. Минимум іздеу де осыған ұқсас жолмен жүргізіледі.
n белгісізі бар біртекті емес сызықты теңдеулер жүйесін қарастырайық:
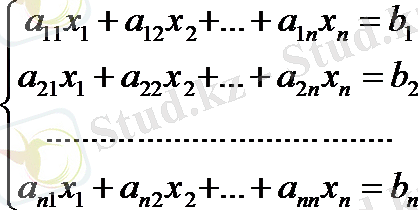 (1)
(1)
Бұл жүйенің белгісіздер саны теңдеулер санына тең, жүйенің негізгі матрицасы nжатық, nтік жолдардан тұрады. Сондықтан жүйенің негізгі матрицасы n-ретті квадрат матрица болады.

А матрицаның анықтауышы берілген сызықты теңдеулер жүйесінің бас анықтауышы деп аталады.
(1) жүйенің анықтауышы нөлге тең болмасын, яғни
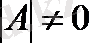
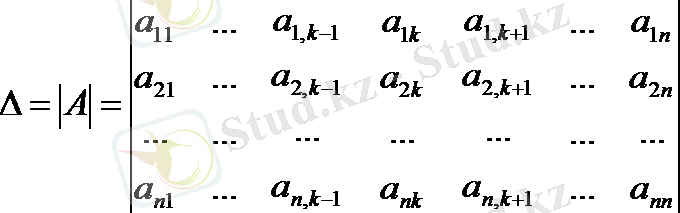
(1) жүйенің бас анықтауышы.
Берілген жүйенің бас анықтауышының бірінші тік жолының элементтері x1 белгісіздің коэффициенттері, ал екінші тік жолдың элементтері x2 белгісіздің коэффициенттері т. с. с. Осы анықтауыштың кез келген тік жолының, мысалы к-тік жолының элементтерін (xк белгісізінің коэффициенттерін) (1) жүйенің сәйкес бос мүшелерімен орын алмастырғанда алынған анықтауышты
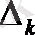 таңбасымен белгілейік:
таңбасымен белгілейік:

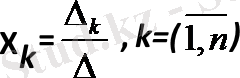
Крамер теоремасы. Егер (1) біртекті емес сызықты теңдеулер жүйесінің негізгі матрицасының анықтауышы нөлге тең болмаса, онда ол анықталған жүйе. Бұл жүйенің шешімі Крамер формуласымен анықталады:
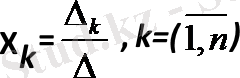 (3)
(3)
(3) - Крамер формулалары деп аталады.
Кері матрица әдісі.
Берілген (1) жүйені кері матрица әдісімен шешу үшін осы жүйенің төмендегі матрицаларын қарастырайық:
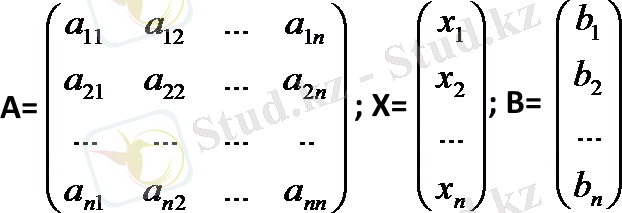
Мұндағы
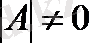 болсын, Х - белгісіз n
болсын, Х - белгісіз n
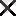 1 өлшемді матрица.
1 өлшемді матрица.
Матрицаларға қолданылатын амалдарға сүйене отырып, А мен Х матрицаларының көбейтіндісі (1) жүйенің сол жағындағы өрнектен анықталған матрицаға тең деп аламыз. Алдымен А мен Х матрицаларының көбейтіндісін анықтайық:
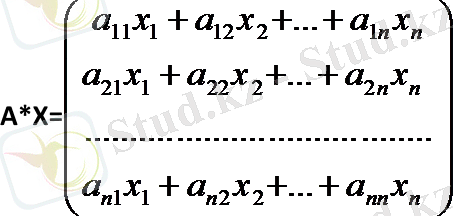
А*Х пен В матрицаларының теңдігінен мына теңдеуді аламыз:
А*Х = В; (4)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz