Математикалық анализ: шектер мен тамаша шектер


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Е. А. Букетов атындағы Қарағанды мемлекеттік университеті
Кафедра: Математиткалық талдау және дифференциалдық теңдеулер
КУРСТЫҚ ЖҰМЫС
Тақырыбы: Тамаша шектер
ЖОСПАРЫ
КІРІСПЕ . . .
I-тарау . Шектер туралы түсінік. Шектердің қолданылу негізі . . .
1. 1Шектер және шектердің қолданылуы . . .
1. 2 Нақты сандар тізбегі жəне оның шегі . . .
1. 3 Функцияның шегі. Функция шегінің анықтамсы
1. 4 Шексіз кішкене және шексіз үлкен сандар. .
II-тарау. Тамаша шектер . . .
2. 1 Тамаша шектер . . .
2. 2 Бірінші тамаша шек . . .
2. 3 Екінші тамаша шек . . .
Қорытынды . . .
пайдаланылған әдебиеттер тізімі . . .
3
5
5
8
14
13
14
14
17
19
22
25
КІРІСПЕ
Математика - нақты өмірдегі сандық қатынастар мен кеңістіктік формалар туралы ғылым.
Математикада математикалық модельдер зерттеледі. Ол нақты құбылыстардың тура математикалық модельдері болуымен қатар осы модельдерді зерттеуге арналған(структуралар) объект болуы мүмкін. Бір математикалық модель тура мазмұны жағынан бір-бірінен қашық жатқан нақты құбылыстардың қасиеттерін көрсетуі мүмкін. Мысалы, бір дифференциалдық теңдеу халықтың өсу процессін де жəне макроэкономикалық динамикасын да көрсетеді. Математика үшін қарастырылып отырған объектілердің табиғи мəні емес, олардың арасындағы қатынастардың маңызы зор.
Математика жаратылыс ғылымдарында, инженер-техникалық жəнегуманитарлық зерттеулерде маңызды роль атқарады. Ол көптеген білім бөлімдерінде тек қана сандық есептеу жасау үшін ғана емес, сонымен қатар дəлірек зерттеудің тəсілі жəне ұғымдар мен проблемалардың шекті тура тұжырымдарын беру құралы болады. Адам өміріндегі əртүрлі салалардағы прогресс жетілдірілген логикалық жəне есептеу аппараты бар қазіргі замандағы математикасыз мүмкін емес.
Математика қолданбалы есептерді шешуге арналған күшті құрал жəне ғылымның əмбебап тілі ғана емес, сонымен қатар ол негізгі мəдениеттің элементі де болып есептеледі. Сондықтанда математикалық білім осы заманға экономистерді фундаментальды дайындау жүйесіндегі маңызды бөлім болады.
Математиканың айтылмыш тараулары, әсіресе математикалық анализ 18ғасырда одан әрі дамыды.
Бұл салада ұлы математиктер Л. Эйлер мен Ж. Лагранж ерекше еңбек сіңірді. Осы ғалымдар мен француз математигі А. Лежандр еңбектерінде сандар теориясы алғаш рет жүйелі ғылым санатына қосылды.
Алгебрада швейцар математигі Г. Крамер (1750) сызықтық теңдеулер жүйесін шешу үшін анықтауыштарды енгізді. Ағылшын математигі А Муавр мен Л. Эйлердің көрсеткіштік және тригонометриялық функциялардың байланысын көрсететін формулалары комплекс сандарды математикадағы қолдану өрісін кеңейте түсті. И. Ньютон, шотланд математигі Дж. Стирлинг, Л. Эйлер және П. Лаплас шектеулі айырымдарды есептеудің негізін қалады. К. Гаусс 1799 жылы алгебраның негізгі теоремасының бірінші дәлелін жариялады.
Математикалық анализ әсіресе дифференциалдық теңдеулер әдістері механика мен физиканың, сондай-ақ техникалық процестердің заңдарын, математикалық өрнектеудің негізін қалады; жаратылыс тану мен техниканың ілгерілеуі осы әдістерге тікелей байланысты болды.
Ағылшын математигі Б. Тейлор (1715) кез келген функцияларды дәрежелік қатарға жіктеу жөніндегі өзінің формуласын ашты. 18 ғасыр математиктері үшін қатарлар анализдің ең бір қуатты, икемді құралына айналды. Л. Эйлер, Ж. Лагранж бірінші ретті, ал Л. Эйлер, Г. Монж, П. Лаплас екінші ретті дербес туындылы дифференциалдық теңдеулердің жалпы теориясының негізін қалады.
Математикалық анализдің ықпалымен аналитикалық механика, математикалық физика т. б. жаңа салалар қалыптаса бастады; математикалық анализдің айрықша бір бұтағы- вариациялық есептеу қалыптасып, маңызды қолданыс тапты. Ағылшын математигі А. Муавр, Я. Бернулли, П. Лаплас 17-18 ғасырлардағы жекелеген нәтижелерге сүйеніп ықтималдықтар теориясының негізін қалады. Геометрия саласында Л. Эйлер элементар аналитикалық геометрия жүйесін жасауды аяқтайды. Л. Эйлер, француз математигі А. Клеро, Г. Монж еңбектерінде кеңістіктегі қисық сызықтар мен беттердің дифференциалдық геометриясының негізі салынды. Неміс ғалымы Ламберт перспектива теориясын дамытты, ал Г. Монж сызба геометрияны аяқталған түрге келтірді.
Қазіргі математика дәуірі. 18 ғасырдың аяғы мен 19 ғасырдың бас кезінен бастап математиканың дамуында бірсыпыра жаңа белгілер мен сипаттар орын алды.
Математиканы негіздеудің көптеген мәселелеріне сын көзбен қайта қарау әрекетіне тоқтайық.
Ол ең әуелі математиканың жаңа тарауларын қамтиды. Шексіз аз шамалар жайлы бұрынғы анық емес бұлдыр түсініктің орнына шек ұғымын дәл анықтайтын тұжырымдар пайда болды (О. Коши, Б. Больцано, К. Вейерштрасс) .
Математикалық анализ бен математикалық физика дамуының геометрия мен алгебрадағы жаңа идеялармен түйіндесуі нәтижесінде математика мен оның қолдануында ерекше маңызды қызмет атқарып отырған математиканың үлкен бір жаңа саласы- функционалдық анализ жасалды. Статистикалық физика мен әр түрлі мәселелерді зерттеуге статистикалық әдістерді кең қолдану әрекеті ықтималдықтар теориясының алдына көптеген жаңа міндеттер қойды. Осы негізде бұл теория 19-20 ғасырларда күшті қарқынмен дамытылды.
I-тарау . Шектер туралы түсінік. Шектердің қолданылу негізі
1. 1 Шектер және шектердің қолданылуы
Тізбек шегі ұғымы, жалпы шек ұғымы, оқушылардың түсініп, меңгеруіне аса күрделі тақырыптардың бірі.
Тізбектің шегі бойынша функцияның шегін қалыптастыру ұзақ уақытты талап етеді, ал оқушылардың назарын аз уақытқа ғана шоғырландыруға болады. Тәуелсіз айнымалы мен тәуелді айнымалылардың ұмтылыстары екі процесс,
Айталық, мұғалім өзіне
Осыдан кейін дербес процестерді бағанға орналастырып функциялардың шектік мәндерін жалпылау керек.

Шек ұғымының келесі проблемасы тілшелерді теңдікке алмастыру. Қосу, алу, көбейту, бөлу сияқты шек те амал. Амалдар арнайы таңбалармен белгіленеді.
Әдетте екі процесті сөзбен тұжырымдап бірден математикалық өрнегін бере салады. Мысалы, былай « шексіздікке ұмтылғанда функцияның ұмтылатын А санын оның шегі дейді және оны былай жазады»:
Бұл анықтама арқылы мақсатқа тез жетуге болады, бірақ процестерден осы теңдікке ауысу кезінде ашылмай қалған ұғымдар бар және шек ұғымын қалыптастыруға көру органы қатыстырылмаудың нәтижесінде оқушылардың санасында күдік сезімі қалып қояды. Күдік болған жерде ұғым қалыптасты деп айту қиын. Күдікті туғызбас үшін төменде көрсетілгендей екі-үш суретті дайындап қою керек.

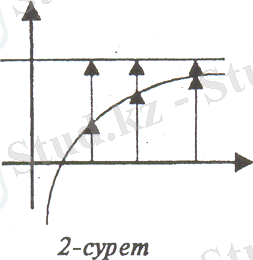
Осы суреттерде қисық сызықтардың ординаталары және функцияның шектік мәндерінің ординаталары көрсетілген. Солар арқылы мына теңдікті жазуға болады.
1-сурет бойынша:
\[\begin{array}{l}{{{\cal M}\bar{A}={\cal M}\bar{A}+{\cal A}\bar{A}\bar{\cal A}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\bar{\Gamma}}}\\ {{\bar{\cal M}\bar{A}-{\hat{\cal O}}\bar{I}+\bar{\cal M}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\mathrm{~}\bar{\cal P}={\cal A}+a\left(x\right)}}\\ {{\bar{\cal B}=\hat{\cal E}\bar{I}\,\,+\bar{\cal I}D\bar{\mathrm{~}\hat{\cal P}}}}\end{array}\mathrm{~}\quad{\cal P}(x)={\cal A}+a\left(x\right)\]( Ш)
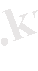 Мұндағы А тұрақты сан, ал
Мұндағы А тұрақты сан, ал
Шектік мән нөлден өзгеше сан болған жағдай үшін бірінші және екінші тамаша шектер деп аталатын формулалар енгізіледі.
Функцияның жуық мәндерінің құрылымдарына талдау жасап алдымен е-нің мәні 2<е<3
 болатындығы туралы туралы, содан кейін е саны иррационал екендігін оқушыларға хабарлайды. Е-нің иррационалдығына мына ақпараттар негіз бола алады: «10-ның көрсеткіші өскен сайын е-нің алдыңғы жуық (көп нүктеге дейінгі) мәндеріндегі цифрлар сақталып, тағы да дәлдігін арттыратын бір цифр қосылып отырады. Ал 10-ның көрсеткіші натурал сандармен өрнектелгіндіктен және олардың құрамында қайталанылатын цифрлар тобы болмағандықтан е-санының құрылымында да қайталанатын цифрлар тобы жоқ». Ендеше функцияның ұмтылатын саны иррационал сан. Оны «е»- мен белгілеп
Непер саны
деп атайды. Енді екі процесте біріктіріп теңдік арқылы былай жазады.
болатындығы туралы туралы, содан кейін е саны иррационал екендігін оқушыларға хабарлайды. Е-нің иррационалдығына мына ақпараттар негіз бола алады: «10-ның көрсеткіші өскен сайын е-нің алдыңғы жуық (көп нүктеге дейінгі) мәндеріндегі цифрлар сақталып, тағы да дәлдігін арттыратын бір цифр қосылып отырады. Ал 10-ның көрсеткіші натурал сандармен өрнектелгіндіктен және олардың құрамында қайталанылатын цифрлар тобы болмағандықтан е-санының құрылымында да қайталанатын цифрлар тобы жоқ». Ендеше функцияның ұмтылатын саны иррационал сан. Оны «е»- мен белгілеп
Непер саны
деп атайды. Енді екі процесте біріктіріп теңдік арқылы былай жазады.
\[\Big|{}_{x\oplus\infty}{\frac{\alpha}{\Theta}}\!\!\!\!\cdot\!\!\cdot\!\frac{1}{1x}{\frac{\alpha}{\phi}}\!\!\cdot\!\stackrel{x}{\phi}\]
Теңдіктері канондық түрде өрнектелген нақты құрылымдардың заңдылықтары (формасы) . Бұларды формулаға айналдырмай есептемеге пайдалануға болмайды. Форманың жалпы түрі формуланы береді.
Оқушылардың қоғамға қажетті шаруашылықтың қай саласында қызмет атқаратындығы бізге беймәлім. Базарларда тұрып сауда-саттықпен айналысуыда мүмкін. Бірақ қай салада қызмет етсе де еңбегінің нәтижелі болуын көздеп олар ой таразысына салып талдайтындығы айқын. Бұл процесс. Процестің элементтерін анықтап, олардағы ақпарларды бір-бірімен салыстырып, өзгеру тенденциясына назар аударып, тиісті қорытынды жасауға үйретуге пайдаланатын оқу құралы осы шек ұғымы. Математикалық ұғымды қалыптастыру тұрғысынан қарастырғанда шек ұғымының атқаратын қызметі ерекше. Өйткені шекті есептеу кезінде математикалық формулалар мен теоремалар жиі айналымға келеді.
1. 2 Нақты сандар тізбегі жəне оның шегі
Анықтама. Натурал сандар жиыны N анықталған f(n) функциясын тізбек деп атайды. Тізбекті былай жазады немесе қысқаша . Мұндағы n ші жалпы мүшесі дейді. Барлық элементтері тек бір ғана саннан тұратын тізбекті тұрақты тізбек деп атайды.
Екі тізбек берілсін және .
Анықтама. Екі тізбектіердің қосындысы, айырмасы, көбейтіндісі деп сәйкесінше, , тізбектердін айтады.
Егер болса, онда тізбекті тізбекке бөлгенде қатынас деп тізбегін айтады.
Анықтамалар:
- Егер үшін тенсіздігі орындалса, онда тізбегі өспелі (кемімелі ) делінеді.
- Егер орындалса, онда тізбегі жоғарғы жағынан шектелген делінеді.
- Егер орындалса, онда тізбегі төменгі жағынан шектелген делінеді.
- Егер тізбегі жоғарғы және төменгі жағынан шектелсе, онда оны шектелген дейді, яғни .
- Егер кез келген саны үшін тізбектің ең болмағанда бір элементі табылып теңсіздігі орындалса, онда тізбекті шектелмеген деп атайды.
Шексіз аз тізбек пен шегі бар тізбектің арасында тығыз байланыс бар: тізбегінің шегін а десек, онда саны үшін, теңсіздігі орындалса да тізбегі шексіз аз болады.
Анықтама Егер тізбегі мен а санының айырмасы шексіз аз болса, онда а санын тізбегінің шегі деп атайды.
Анықтама. Егер кез келген санына сәйкес N номері табылып барлық мәндерінде теңсіздігі орындалса, онда тізбегін шексіз үлкен тізбек дейді де деп жазады.
Шексіз үлкен және шексіз аз тізбектірдің арасындағы байланыс.
Теорема 1. Егер тізбегі шексіз үлкен болса, онда қандай да бір n нөмерінен бастап, екі тізбегінің қатынасы анықталады да ол шексіз аз тізбек болады.
Теорема 2. Егер тізбегі шексіз аз болса, онда қандай да бір n нөмерінен бастап, екі тізбегінің қатынасы анықталады да ол шексіз үлкен тізбек болады.
Теорема 3. Егер және тізбектері шексіз аз болса, онда олардың қосындысы (айырмасы) шексіз аз тізбек болады.
Салдар. Саны шекті шексіз аз тізбектердің алгебралық қосындысы шексіз аз тізбек болады.
Теорема 4. Шектелген тізбек пен шексіз аз тізбектің көбейтіндісі шексіз аз бллады.
Теорема 5. Кез келген аз тізбек шектелген.
Салдар. Саны шекті шексіз аз тізбектердің көбейтіндісі де шексіз аз тізбек болады.
Теорема 6. Егер шексіз аз тізбегінің барлық элементтері бір және тек бір ғана с санына тең болса, онда с=0.
Жинақты тізбектердің қасиеттері.
Теорема 1. Жинақты тізбектердің тек бір ғана шегі болады.
Теорема 2. Кез келген жинақты тізбек шектелген.
Ескерту. Кез келген шектелген тізбек жинақты болады деуге болмайды.
Теорема 3. Жинақты мен тізбектердің қосындысы (айырмасы) да жинақты тізбек және оның шегі мен тізбектер шектерінің қосындысына (айырмасына) тең
Салдар. 3 ші теорема косылғыштырдың саны шекті болған жағдайда да күшін сақтайды
Ескерту. 3 теореманың кері тұжырымы әр уақытта дұрыс бола бермейді, яғни қосындының шегінің бар болуынан әрбір қосылғыштың шегі бар деуге болмайды.
Теорема 4. Егер мен тізбері жинақты болса, онда тізбегі де жинақты және оның шегі мен тізбітер шектерінің көбейтіндісіне тең
Салдар. Егер бар болса, онда, мұндағы к кез келген тұрақты сан, шегі де бар және =.
Салдар. Саны шекті жинақты тізбектердің көбейтіндісі де жинақты болады.
Ескерту. 4 тоермаға кері теорема әрқашанда орынды деуге болмайды. Басқаша айтқанда тізбегінің шегі бар балғанымен мен тізбектерінің шектері болмауы мүмкін.
Теорема 5. Егер мен тізбектерінің шектері сәйкес а және в болса, онда тізбегінің де шегі бар және .
Салдар. Егер және, к - бүтін теріс сан болса, онда
Теорема 6. Егер, , к натеурал сан болса, онда
Анықтама. Егер тізбегінің әрбір келесі элементті оның алдындағы элементтен кем /артық/ болмаса, яғни егер барлық нөмерлері үшін // теңсіздігі орындалса, онда тізбегін кеміммейтің /өспейтің/ тізбек деп атайды.
Анықтама. Егер тізбегінің әрбір келесі элементті оның алдындағы элементтен кем /артық/ болмаса, яғни егер барлық нөмерлері үшін // теңсіздігі орындалса, онда өспелі /кемімелі/ тізбек деп атайды.
Тізбетердің барлық осы түрлерін біріктіріп жалпы атпен монотонды тізбектер деп атайды.
Кез келген монотонды тізбек не жоғары, не төменгі жағынан шектелген болады.
Егер өспейтін тізбек төменгі жағынан шектелсе, онда ол екі жағынан да шектелген болады.
Теорема. Егер кемімейтін /өспейтін/ тізбек жоғарғы /төменгі / жағынан шектелсе, онда ол жинақты.
Салдар. Монотонды тізбек жинақты болу үшін оның шектелуі қажетті және жеткілікті.
1 ескерту. Жинақты тізбек монотонды болмауы да мүмкін.
2 ескерту. Кемімйтін және жоғарғы жағынан шектелген тізбегінің барлық элементтері оның шегі а дан аспайды, яғни .
3 ескерту. Монотонды тізбектің шегі тұралы теоремада шектің бар болуы фактысы ғана тағайындалган, ал шекті табу әдісі көрсетілмеген.
Анықтама Егер кесінділердің шексіз тізбегі үшін
1/ Әрбір келесі кесінді оның алдындағы кесіндіде жатса
/1/
2/ кесіндісінің ұзындығы нөлге ұмтылса, яғни, онда /1/ тізбекті тартылатын кесінділер деп атайды.
Теорема. Егер /1/ тізбек тартылатын кесінділер тізбегі болса, онда осы кесінділірдің бәрінде жататын с нүктесі бар және ол жалғыз.
е саны. Мынадай тізбек алайық та, монотонды тізбектің шегі теореманы пайдаланып осы тізбектің жинықты екенін дәлелдейік.
Оны бинома ньютон формуласын пайдаланып жиктейміз.
x n+1 элементті сол сияқты жазамыз
Мунда x n < x n+1 , яғни { x n } тизбегі өспелі болады.
Енді бұл тизбектін жоғарыдан шектелетіндігінін көрсетеміз. Для доказательства ограниченности этой последовательности сверху заметим, что каждое выражение в круглых скобках в соотношении меньше единицы. Учитывая также, что <при ≥ 2, получим
<< 3
Сонымен { x n } тизбегі өспелі және шектелген жоғары жағынан. Онда { x n } тизбегінін шегі бар. Ол шекті және оны е арқылы белгілейді, яғни . Бұл санның анализдің өзі үшін де және онын қолданылуында да маңызы. (Эйлердің саны), е саны иррационал және сол себептен шексіз периодты емес бөлшек. Ол логарифмдер негізіне алынған, негізгіе е болатын логарифмдер натурал логарифмдер деп атайды. санының натурал логарифмін lnx деп белгіле»ді, яғни lnx=
1. 3 Функцияның шегі. Функция шегінің анықтамсы.
x саны x 0 санына ұмтыла берсін, бірақ оған тең болмасын. Бұны x→x 0 деп белгілейміз.
Мысалы мына сандар тізбегінің n -ші мүшесі, n өскен сайын нөлге ұмтылады (бірақ нөлге тең болмайды) :
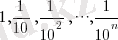 , …
, …
Аңықтама.
A саны y=f(x) функциясының x→x 0 ұмтылғандағы шегі деп аталады, егер x 0 санына ұмтылған кез келген x 1 , x 2 , x 3 , … сандар тізбегі үшін сәйкесінше f(x 1 ), f(x 2 ), f(x 3 ), … сандар тізбегі A санына ұмтылса.
Бұны
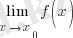 = A деп белгілейді.
= A деп белгілейді.
Мысал.
y = x
2
болса онда
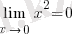 . Өйткені нөлге ұмтылған кез келген
x
1
, x
2
, x
3
, …
сандар тізбегі үшін
x
1
2
, x
2
2
, x
3
2
, …
сандар тізбегі де нөлге ұмтылады ғой.
. Өйткені нөлге ұмтылған кез келген
x
1
, x
2
, x
3
, …
сандар тізбегі үшін
x
1
2
, x
2
2
, x
3
2
, …
сандар тізбегі де нөлге ұмтылады ғой.
1) .
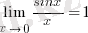 (
бірінші тамаша шек
) .
(
бірінші тамаша шек
) .
2) .
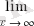 (1+
(1+
 )
x
=
e
, мұндағы
e
)
x
=
e
, мұндағы
e
 2, 718… (
екінші тамаша шек
) .
2, 718… (
екінші тамаша шек
) .
Аңықтама.
y=f(x) функциясы:
a) . x 0 нүктенің белгілі бір маңайында аңықталса.
b) .
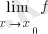 (x) =
(x) =
 (x
0
)
(x
0
)
Онда y=f(x) функциясы x 0 нүктеде үзіліссіз деп аталады.
Мысал.
y = x
2
функциясы
x=0
нүктеде үзіліссіз, өйткені бұл функция біріншіден осы нүктенің аймағында аңықталған, екіншіден
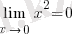 , y(0) = 0, яғни
, y(0) = 0, яғни
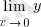 (
x
) = y (0)
(
x
) = y (0)
Аңықтама.
y=f(x) функциясы B сандар жиынының кез келген нүктесінде үзіліссіз болса, онда бұл y=f(x) функциясы B сандар жиынында үзіліссіз деп аталады.
Мысал.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz