Қос күш: анықтамасы, моменті және қасиеттері


КІРІСПЕ
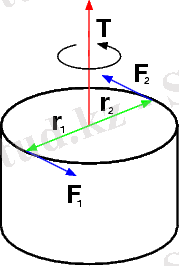
Абсолют қатты дененің А және В нүктелері шамалары тең, бағыттары параллель қарама-қарсы Р, Р күштері түсірілген дейік. Мұндай екі күштің системасы бір тең әсер етуші күшке келтірілмейді және тепе-теңдікте болмайды. Шынында да құраушы күштерге параллель тең әсер етуші күш R болса, онда оның әсер ету сызығы АВ түзуін А нүктесінен
АС =Р . АВ
R
қашықтықта қиып өтер еді. Ал
R = Р- Р = 0
болғандықта. Модулі нольге тең күштің тусу нүктесі шексіздікте жатуы мүмкін емес. Осымен қатар құраушы күштерге параллель емес тең әсер етушінің де болуы мүмкін. Өйткені мұндай тең әсер етуші күші бар десек, қос күш күшімен теңесумен керек. Тепе-теңдіктегі үш күштің
0 әсер ету сызықтары бір нүктеде қиылысу қажет. Р және Р антипараллель күштер болғандықтан бұл шарт орындалмайды. Сонымен, тең шамалы антипараллель екі күш ешбір жеке күшпен теңгерілмейді. Осындай екі күштен тұратын күш системасын қ о с к ү ш деп атайды.
Қос күш- жаңа статикалық элемент, денелердің механикалық өзара әсерінең жаңа өлшеуші. Күш ұғымымен қатар қос күш механикадағы негізгі ұғымдардың бірі болып табылады. Сондықтан қос күш қасиеттері өз алдына
жеке қарастырылуы қажет. Сонымен, шамалары өзара тең параллель қарамы-қарсы бағытталған екі күштің системасын қ о с к ү ш күш дейміз.
НЕГІЗГІ БӨЛІМ
2. 1. Қос күш моменті
Қос күш әсері қос күш моментімен анықталады. Моментті қос күш айналдырушы әсерінің үш түрлі сипаттамасын түгел қамтитыңдай етіп анықтауымыз керек. Сондықтан да қос күш моментіне векторлық анықтама беруге тйістіміз. Қос күш моментті деп - модулі күш пен иін көбейтіндісіне (Ph) тең, ал бағыты қос күш бағыты жазықтығына перпендикуляр болып келетің векторды айтамыз. Қос күш моменті Нм (ньютон метр) өлшемімен өлшенеді. Қос күш моменті векторының бағытын анықтауда оң бұрғы ережесі қолданылады. Қос күш моментінің вектарын m (P, P) деп белгілесек, онда оның модулін қос күш күші мен иінінің көбейтіндісіне теңестіреміз.
m(P, P) =Ph=P h
Бұл теңдіктен ол вектордың модулінің P, P күштерінен құрылған параллеограмм ауданына тең болатындығын көреміз.
m(P, P) =S abcd=Ph
m (P, P ) векторы - еркің вектор, оны қос күш әсер ететін дененің кез келген бір нүктесіне түсіруге болады. Бұл вектордың осы қасиетің алдағы жерде дәлелдеп көрсетеміз.
Әдетте келісім бойынша ол вектор қос күштерінің бас нүктелері қосатын АВкесіндісінің ортасына түсіріледі.
Енді жоғарыда берілген анықтама сәйкес қас күш моментінің векторлық өрнегін тағайындауымыз қажет. Сол мақсатпен мынадай векторлық көбейтінді аламыз.
ABхP, немесе BAхP
Бұл векторлық көбейтіндінің модулі мен бағытын анықтайық. Оның модулін
көрсетілген қос күштің иіні болып табылады Һарқылы өрнектейік. Сонда алатынымыз:
AB х P=AB P sin (AB, P ) =Ph
Бұл теңдігін қос күш моменті векторының модулін анықтайтын немесе теңдігімен салыстырып қарасақ, одан екі вектордың модульдерінің тен болатындығын көреміз:
AB х P = +m (P, P)
Осыдан кейін AB х P векторының бағытына көңіл бөлеміз. Бұл вектор АВСД параллеограмның жазықтығын (немесе Q жазықтығына ) тұрғызылған перпендикуляр мен оң бұрғы ережесіне сәйкес бағытталады. Демек AB х P ( немесе BA х P ) векторы мен қос күш моментінің векторы бірдей бағытталады. Осы салыстырудан AB х P ( BA х P ) векторының векторына тең болатының тағайындаймыз. Олай болса қос күш моментінің m (P, P ) векторың АВ және Р (немесе ВА және Р) векторларының векторлық көбейтіндісімен өрнектей аламыз.
2. 2. Қос күш моментінің қасиеттері
a) Қос күш моменті құраушы күштердің кез келген бір центрге қатысты алынған моменттерінің геометриялық қосындысына тең*2
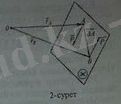
Қос күшті құраушы
 және
және
 күштерінің кез келген О центріне қатысты моментінің (2 сурет) қосындысын есептейік:
күштерінің кез келген О центріне қатысты моментінің (2 сурет) қосындысын есептейік:
.
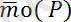 +
+
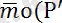 ) =
) =
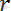 A
х
A
х
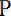 +
+
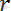 B
х
B
х
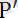 = (
= (
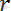 A
-
A
-
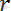 B
) х
B
) х
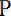 =
=
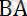 х
х
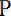 (5)
(5)
Мұнда біз
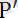 = -
= -
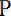 және
және
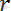 A
-
A
-
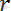 B
=
B
=
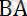 қатынастарын ескердік. (5) теңдігін қос күш моментінің анықтамасын сипаттайтын, (4) теңдігімен салыстырайык . Бұлардың оң жақтары тең. Осыдан
қатынастарын ескердік. (5) теңдігін қос күш моментінің анықтамасын сипаттайтын, (4) теңдігімен салыстырайык . Бұлардың оң жақтары тең. Осыдан
 (
(
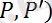 =
=
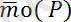 +
+
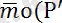 ) (6)
) (6)
(6) теңдігі қос күш моментінің құраушы күштердің кез келген центрге қатысты моменттерінің қосындысына тең екенін дәлелдейді. б) Қос күштің моменті оның бір күшінің әсер ету сызығының кез келген нүктесіне қатысты алынған моментіне тең. Осыны дәлелдеу үшін қос күштің бір күші
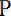 -ның екінші
-ның екінші
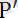 күшінің әсер ету сызығының бойында жатқан В нүктесіне қатысты моменті
күшінің әсер ету сызығының бойында жатқан В нүктесіне қатысты моменті
 B
(
B
(
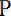 ) векторын табуымыз керек. Жоғарыдағы (6) формуланы В нүктесіне қатысты алайық
) векторын табуымыз керек. Жоғарыдағы (6) формуланы В нүктесіне қатысты алайық
 (
(
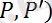 =
=
 B
(
B
(
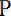 ) +
) +
 B
B
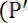 ) (7)
) (7)
B нүктесі
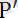 күшінің әсер ету сызығында жатқандықтан
күшінің әсер ету сызығында жатқандықтан
 B
B
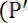 ) =0 болады да (7) теңдіктімына түрде келтіреміз.
) =0 болады да (7) теңдіктімына түрде келтіреміз.
 (
(
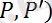 =
=
 B
(
B
(
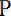 ) (8) сол сияқты
) (8) сол сияқты
 (
(
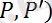 =
=
 A
(
A
(
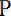 ) +
) +
 A
A
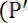 ) =
) =
 A
A
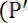 ) (9)
) (9)
Сонымен (8) (9) теңдіктерін өзара салыстырудан алатынымыз
 (
(
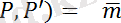 A
A
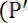 ) =
) =
 B
(
B
(
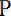 ) (10)
) (10)
(10) қатынасы қос күш моменті оның бір күшінің екінші күш бойында жатқан кез келген бір нүктеге қатысты алынған моментіне тең екенін көрсетеді.
2. 2. 1. Қос күштер эквивалеттілігі
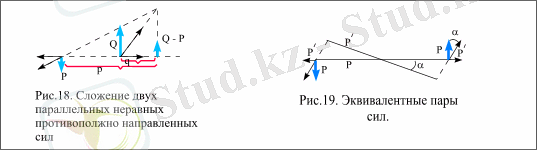
а) Қос күшті қатаң фигура тәрізді өз жазықтығында бір орыннан екінші орынға параллель тасымалдауғажәне кез келген бұрышқа бұруға болады. Бұдан қос күштің қатты денеге әсері өзгермейді
б) Қос күштің жазықтығын параллель көшіруге болады. Бұдан қос күштің қатты денеге әсері өзгермейді.
в) Қос күштің иінін және күшің, олардың көбейтіндісі өзгермейтіндей етіп, өзгерген түрде алуға болады. Бұдан қос күштің қатты денеге жасайтын мех-қ әсері өзгермейді.
2. 2. 1. Вариньон теоремасы
Күштердің жазық жүйесі
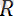 ≠0,
≠0,
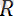 *
*
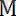 0
= 0 шарттары орындалған жағдайда теңәсерлі бір күшке келтіріледі. Бұл жағдайдағы күштердің жазық жүйесіне Вариньон теоремасын қолдануға болады.
0
= 0 шарттары орындалған жағдайда теңәсерлі бір күшке келтіріледі. Бұл жағдайдағы күштердің жазық жүйесіне Вариньон теоремасын қолдануға болады.
Теорема: Күштердің жазық жүйесінің теңәсерлі күшінің, осы күштер жатқан жазықтыққа алынған, кез келген бір центрге қатысты моменті жүйедегі барлық күштердің сол центрге қатысты моменттрінің қосындысына тең болады.
Қатты денеге әсер етіп тұрған (
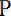 1
,
1
,
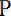 2
,
2
,
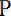 3
, . . . ,
3
, . . . ,
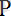 n
) күштердің жазық жүйесі О
*
келтіру центрінде бір теңәсерлі
n
) күштердің жазық жүйесі О
*
келтіру центрінде бір теңәсерлі
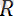 *
күшке келтірілген болсын. Бұл күш, жүйенің бас векторларынга тең
*
күшке келтірілген болсын. Бұл күш, жүйенің бас векторларынга тең
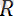 *
=
*
=
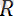 =
=
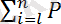 l
және оның әсер ету сызығы О
*
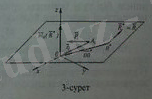
нүктесін басып өтеді(3-сурет) .
l
және оның әсер ету сызығы О
*
нүктесін басып өтеді(3-сурет) .
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz