Ауырлық центрі

Пән: Физика
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 13 бет
Таңдаулыға:

Жоспар

1. Ауырлық центрін табу әдістері. 3

2. Кейбір жиі кездесетін біртекті денелердің ауырлық центрі6

3. Параллель күштер центрі. Бір жаққа бағытталған екі параллель күшті қосу10

4. Қатты дененің ауырлық центрі. Бір текті денелер ауырлық центрінің координаттары. 11

Пайдаланылған әдебиеттер:14

Ауырлық центрін табу әдістері.

Ауырлық центрі [1] немесе Масса центрі - жүйені қозғалтқан кезде жүйенің барлық массасы жинақталған материалдық нүкте сияқты қозғалатын механикалық жүйедегімассаның таралуын сипаттайтын нүкте[2], қатты дененің кеңістіктегі кез келген қалпында оның бөлшектеріне тең әсерлі күшпен түсетін ауырлық күшінің геометриялық нүктесі; бұл нүкте кей жағдайда осы дененің ешбір нүктесімен сәйкес келмеуі мүмкін (мысалы, сақинада) . Біртекті ауырлық өрісіндегі қатты дененің ауырлық центрі оныңмассалар центріне сәйкес келеді. Денені салмақтары p ₁ , p ₂ , . . . , pn болатын бөліктерге бөліп, олардың ауырлық центрі лерінің (х ₁ , у ₁ , z ₁ ), (x ₂ , y ₂ , z ₂ ), . . . координаттары арқылы, сол дененің ауырлық центрінің координаттарын (х _с , у _с , z _c ) мына формуламен анықтауға болады:

X _c = (p ₁ x ₁ + p ₂ x ₂ + . . . pnxn) / (p ₁ + p ₂ + . . . pn)
Y _c = (p ₁ y ₁ + p ₂ y ₂ + . . . pnyn) / (p ₁ + p ₂ + . . . pn)
Z _c = (p ₁ z ₁ + p ₂ z ₂ + . . . pnzn) / (p ₁ + p ₂ + . . . pn)

Симметрия центрі бар біртекті дененің (тікбұрышты немесе дөңгелек пластина, шар, цилиндр, куб т. б. ) ауырлық центрі сол дененің симметрия центрінде жатады. [3]

Массалар центрі , ауырлық центрі - дене қимылын немесе бөлшектердiң жүйесін сипаттайтын геометриялық нүкте; қатты дененің кеңістіктегі кез келген жағдайында оның бөлшегіне әсер ететін барлық ауырлық күштерінің қорытқы күші өтетін қатты денемен өзгеріссіз байланысты нүкте. [1]

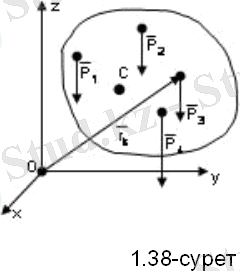
қатты дене n бөлшектерден тұрады дейік (1. 38-сурет) . Сонда, жердің центріне қарай бағытталған, бөлшектердің n ауырлық күштері 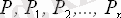аламыз. Егер дененің өлшемдері жердің радиусына қарағанда әлдеқайда кіші шама болса, онда 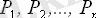күштерін өзара параллель бағытталған күштер деп алуға болады.

Дене бөлшектерінің ауырлық күштерінен тұратын 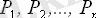параллель күштер жүйесінің центрін дененің ауырлық центрі деп атаймыз.

Демек, қатты дененің ауырлық центрінің орны мына формуламен табылады:

(1. 80)

Дененің ауырлық центрі С -ның координаттарын x _с , y _c , z _c , деп белгілесек, онда (1. 80) векторлық теңдеуден мына формулаларды табамыз:

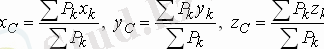(1. 81)

(1. 81) - формулалары дененің ауырлық центрінің координаттарын береді.

1) Симметрия әдісі. Егер біртекті дененің симметрия жазықтығы немесе өсі немесе центрі бар болса, онда бұл дененің ауырлық центрі оның симметрия жазықтығында немесе өсінде, немесе центріде жатады.

2) Топтау әдісі. Егер берілген дененің тұлғасы күрделі болса, онда оны ауырлық центрлері оңай табылатындай бірнеше бөлікке бөлеміз. Осы бөліктердің ауырлық центрлерін жеке-жеке тауып алған соң бүтіндей берілген дененің ауырлық центрін табамыз. Мысалы, берілген денені үш бөлікке бөлдік дейік. Олардың С ₁ , С ₂ және С ₃ ауырлық центрлерінің радиус-веторларын алдын-ала есептеп алу оңай болсын. әрбір бөлік үшін (1. 80) - ді қолдансақ:

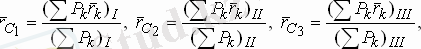(1. 82)

(1. 80) - ді енді берілген бүтіндей денеге қолдансақ

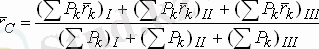(1. 83)

Егер әр бөліктің салмақтарын ескерсек, онда соңғы (1. 83) формуланы (1. 82) -нің негізінде былай жаза аламыз

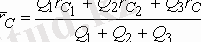(1. 84)

Осы (1. 84) теңдігінен дененің ауырлық центрінің координаттарын таба аламыз:

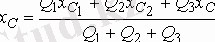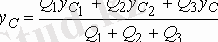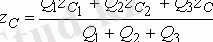Мұндағы 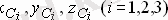денені құрайтын үш бөліктің әрқайсысының ауырлық центрлері С ₁ , С ₂ және С ₃ -тің координаттары. Ал 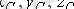бүтіндей алынған дене ауырлық центрінің координаттары.

3) Теріс массалар әдісі. Егер бірнеше бос қуыстары және тесіктері бар дене берілген болса, ол бос қуыстарды дене қандай заттардан тұрса, сондай заттармен ойша толтырамыз да, денені ешбір бос қуысы жоқ бүтін дене деп аламыз. қуыстары мен тесіктері массалармен ойша толтырылған дененің ауырлық центрінің радиус-векторын деп, ал ауырлығын Q деп белгілейік.

Берілген жағдайға келу үшін тесік және қуыстарды екінші ретте қайтадан теріс таңбалы массалармен толтырдық дейміз, бұл теріс массалы қуыстардың самақтарын 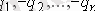, ал олардың радиус-векторларын 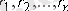деп белгілейік. Сонда бізге берілген дене n+1 бөліктен тұратын болады. Осы денеге топтау әдісін қолданайық. (3) формуласына сүйенсек:

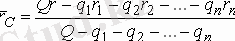Сонда берілген дененің ауырлық центрінің координаттары:

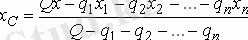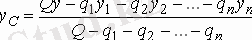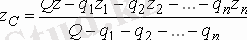Егер біртекті дененің ауырлық центрі қарастырылатын болса, онда қуыстарды теріс таңбалы көлемдер немесе теріс таңбалы аудандар деп есептейміз.

4. Интегралдау әдісі. Егер денені ауырлық центрлері оңай табылатын бөлшектерге бөлуге болмаса, онда оны өте кіші элементар 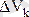көлемдерге бөледі. Олар үшін (1. 8. 8) өрнек мына түрге келеді:

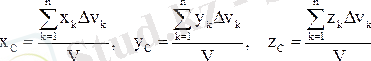(1. 8. 11)

мұндағы 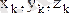- 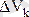элементар көлем ішіндегі нүкте координаталары.

Одан кейін (1. 8. 11) теңдіктеріндегі барлық 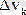элементар көлемдерді нөлге ұмтылдырып, шекке өтеді, яғни осы көлемдерді бір нүктеге жинайды. Сонда теңдіктердегі қосындылар бүкіл көлемге таралған интегралдарға айналады да (1. 8. 11) теңдіктері мынаны береді:

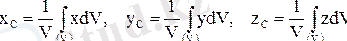. (1. 8. 12)

Осы сияқты, аудан мен сызықтың ауырлық центрлерінің координаталары үшін (1. 8. 9) және (1. 8. 10) өрнектерінен мына өрнектерді аламыз:

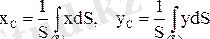. (1. 8. 13)

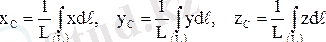. (1. 8. 14)

Осы өрнектерді ауырлық центрінің координаталарын анықтағанда қолдану мысалдары төменде қарастырылады.

5. Эксперименталдық әдіс. Күрделі формалы біртекті емес денелердің ауырлық центрін табу үшін, денені (самолет, паровоз және т. б. ) сым арқанмен оның әртүрлі нүктелерінен іліп қою әдісін пайдаланады. Дене ілінген жіп бағыты ауырлық күшінің бағытын береді. Осы сызықтардың қиылысқан нүктесі дененің ауырлық центрі болады.

Кейбір жиі кездесетін біртекті денелердің ауырлық центрі

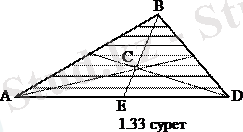
Үшбұрыш ауданының ауырлық центрі. 1. 33 суреттегі 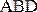үшбұрышы ауданын 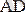қабырғасына параллель түзу сызықтармен жіңішке жолаққа бөлейік. Әр жолақтың ауырлық центрі оның ортасында болады. Олай болса үшбұрыш ауданының ауырлық центрі 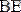медианасында жатады. Қалған екі медиана үшін де дәл осындай нәтиже аламыз. Демек, біртекті үшбұрыш ауданының ауырлық центрі (С нүктесі) оның медианаларының қиылысу нүктесінде жатады екен. Олай болса:

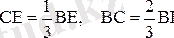. (1. 8. 15)

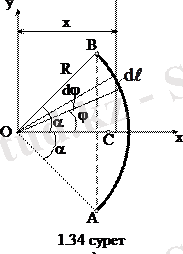
Шеңбер доғасының ауырлық центрі. Центрі О нүктесінде болатын, радиусы R, орталық бұрышы 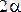-ғатеңАВ шеңбер доғасын қарастырайық. Симметрия өсі бар болғандықтан доғаның ауырлық центрі осы өсте жатады (1. 34 сурет) . Ауырлық центрінің 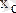координатасын (1. 8. 13) өрнектерді қолданып табамыз. Ол үшін АВ доғасының бойынан орны бұрышымен

анықталатын, ұзындығы 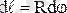элементті бөлеміз. Бұлэлементтің х координатасы: 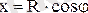. Енді хпен 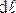-дің мәндерін (1. 8. 14) өрнектерінің біріншісіне қойып, доғаның ұзындығы бойынша интеграл аламыз. Сонда:

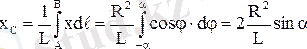
мұндағы 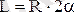- АВ доғасының ұзындығы.

Нәтижесінде, шеңбер доғасының ауырлық центрі оның симметрия өсінде, О центрінен мынандай қашықтықта жататынын табамыз:

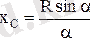. (1. 8. 16)

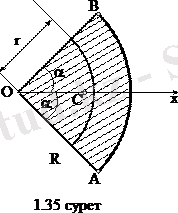
3. Дөңгелек сектор ауданының ауырлық центрі. Радиусы R, орталық бұрышы 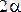-ғатеңОАВдөңгелек секторды қарастырайық (1. 35 сурет) . ОАВдөңгелек сектордың ауданын ойша О центрінен жүргізілген радиустармен секторға бөлейік. Секторлардың санын шексіз көбейткенде оларды ауырлық центрі радиусы 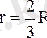доғаның бойында жататын жазық үшбұрыштар деп қарастыруға болады. Демек, (1. 8. 16) - шеңбер доғасының ауырлық центрініңөрнегін пайдаланып дөңгелек сектор ауданының ауырлық центрін анықтайтын өрнек аламыз:

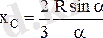. (1. 8. 17)

4. Конус көлемінің ауырлық центрі. Ыңғайлы болу үшін биіктігі симметрия өсі болатын дөңгелек конусты қарастырайық. Конустың шыңын координатаның бас нүктесі етіп, Oz өсін конустың симметрия өсімен бағыттаймыз (1. 36 сурет) . Конусты Oz өсіне перпендикуляр элементар жіңішке дискілерге бөліп, қалыңдығы dz және ауданы S _z бір дискіні қарастырайық.

Бұл диск басқа дискілер сияқты конустың табанына ұқсас. Конусты біртекті деп алып, оның z _C координатасын (1. 8. 12) өрнегі бойынша санаймыз:

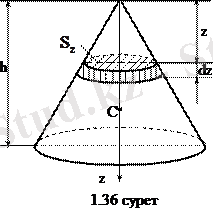
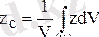. (1. 8. 18)

Қиманың сызықтық өлшемдерінің конус табанының сәйкес өлшемдеріне қатынасы олардың конус шыңына дейінгі ара қашықтықтарына пропорционал, аудандардың қатынасы ара қашықтықтар квадратына пропорционал, яғни

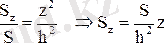
Егер 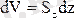, ал конустың көлемі 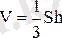екенін ескерсек мынаны аламыз:

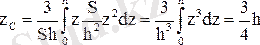немесе .

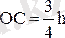Бұл өрнек кез келген конустың немесе пирамиданың көлемі үшін де орын алады. Демек, біртекті конус немесе пирамида көлемінің ауырлық центрі оның табанынан табан ауданының ауырлық центрін конус немесе пирамидашыңымен қосатын түзудің бөлігінде жатады.

Параллель күштер центрі. Бір жаққа бағытталған екі параллель күшті қосу .

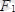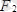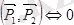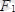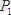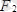Дененің А және В нүктелеріне сәйкес бір жаққа бағытталған және күштері қойылған болсын (7. 1 сурет) . А және В нүктелеріне әсер сызықтары АВ -да орналасқан жүйені қоямыз. Нәтижеде А нүктеде және , ал В нүктеде және 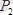күштері пайда болады. Оларды 4 аксиомаға сәйкес қосып, 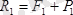және күштерді табамыз. және күштерінің әсер етуші сызықтарының қиылысу нүктесін О деп белгілеп, оларды 3 аксиомадағы теоремаға сәйкес О нүктеге көшіреміз.

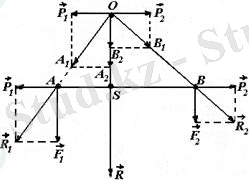Одан кейін 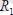-ді, 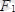, 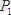; сондай-ақ 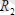-ні 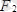, 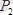күштерге жіктейміз. Бұл кезде О нүктеде бір түзу бойымен бағытталған 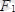және 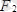күштер пайда болады. Оларды алгебралық қосып, тең әсерлі күшті анықтаймыз

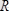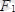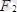= + (7. 1)

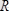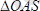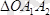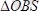Енді - ді әсер сызығы бойымен S нүктеге көшіреміз. 7. 1 суреттегі және , және 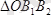ұқсас болғандықтан.

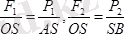(7. 2)

болады.

7. 1 сурет

(7. 2) ден: 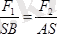, (7. 3)

(7. 3) тен пропорция құрсақ:

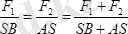
немесе

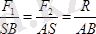(7. 4)

Демек, бір жаққа бағытталған екі параллель күштің тең әсерлісі олардың алгебралық қосындысына тең болып, бағыты осы күштер бағытында, ал әсер сызығы күштер қойылған нүктелер арасындағы қашықтықты ішкі түрде осы күштерге кері пропорционал бөліктерге бөледі.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.