Логикалық элементтер және Вейч-Карно картасы арқылы логикалық функцияларды минимизациялау


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:
МАЗМҰНЫ
КІРІСПЕ
НЕГІЗГІ БӨЛІМ
1 ЛОГИКАЛЫҚ ЭЛЕМЕНТТЕР ЖӘНЕ ОЛАРДЫҢ ТҮРЛЕНУІ . . . 4
2 ЛОГИКАЛЫҚ ФУНКЦИЯЛАРДЫ ВЕЙЧ-КАРНО ӘДІСІМЕН МИНИМАЛИЗАЦИЯЛАУ ПРИНЦИПІН ЗЕРТТЕУ . . . 8
2. 1 Логика функцияларын минимизациялау және оны қарастырғандағы шектеулер . . . 8
2. 2 Вейч-Карно картасы көмегімен минимизациялау әдісі . . . 10
ҚОРЫТЫНДЫ
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІКІРІСПЕ
Қазіргі кезде ЭЕМ-дерінде ақпаратты қабылдайтын, өңдейтін мыңдаған логикалық элементтер (электрондық схемалар) бар. Оларға информация электр сигналдары түрінде беріледі де, схемаларда жоғарғы деңгейлі кернеу (U) I-ге, төменгі деңгейлі кернеу 0-ге теңестіріледі. Логикалық элементтердің ең қарапайым түрлері: ЕМЕС, ЖӘНЕ, НЕМЕСЕ. Осы элементтердің әрқайсысының белгілері бар.
I - ші логикалық элемент-ЕМЕС (не, not) . ЕМЕС элементінің белгілері: ЕМЕС қарсы мән беретін элемент, оның бір кірісі және бір шығысы бар. Егер кіріске сигнал берілсе, онда шығыста сигнал мүлдем болмайды. Ал кірісте сигнал жоқ болса, онда шығысқа сигнал түседі.
II - ші логикалық функция - ЖӘНЕ (и, and) . ЖӘНЕ конъюкцияны беретін элемент: онда екі немесе бірнеше кірістер және бір шығысы бар. Егер кірістерге сигнал берілсе, онда шығысқа да сигнал түседі. ЖӘНЕ элементінің көмегімен бірігетін А және В пікірлері логикалық көбейту немесе осы пікірлердің конъюкциясы деп аталады.
Жұмыстың мақсаты: логикалық функцияларды Вейч-Карно әдісі арқылы минимализациялау принципін анықтау болып табылады.
Жұмыстың міндеті: логикалық функцияларды зерттеу, оларды минимализациялау әдістерін қарастыру. Вейч-Карно әдісі арқылы минимализация принципін зерттеу.
1 ЛОГИКАЛЫҚ ЭЛЕМЕНТТЕР ЖӘНЕ ОЛАРДЫҢ ТҮРЛЕНУІ
Логикалық элементтер - логика алгебрасы ережелеріне сәйкес кіріс сигналдарымен қарапайым логикалық операцияларды (функцияларды) жүзеге асыратын электрондық құрылғылар. Осындай операцияларға логикалық қосу - ''дизъюнкция'' (“немесе”), көбейту - ''конъюнкция''(“және”), терістеу - ''инвертирлеу''' (“емес”) жатады. Ақпараттық сигналдар ретінде электр кернеуі немесе тогының дискреттік мәндері (деңгейлері) қолданылады. Мысалы:
- 0 - төмен деңгейге, 1 - жоғары деңгейге сәйкес келеді. Логикалық элементтер функционалдық белгіленуі, ақпарат беру әдісі, сұлбатех. шешімі және пайдаланылатын электрондық құралдары бойынша ажыратылады. Күрделі Логикалық элементтер қарапайым операциялар орындайтын элементтерді біріктіру арқылы жасалады. Мысалы:
- “немесе” - “емес”, “және - емес”, “немесе - және - емес”, т. б. Құрылымдық түрде Логикалық элементтер жекеленген (дискретті) құраушылардан немесе интегралдық сұлба шала өткізгіш, [ (ИС) түрінде гибридті, үлдірлі орындалуы мүмкін. Қазіргі дербес компьютерлерде жоғары дәрежелі интеграциясы бар ИС-дағы Логикалық элементтер жүйелері қолданылады. Логикалық элементтер компьютерлердің, цифрлық автоматтардың элементтік негізін қалайды.
Сандық құрылғыны жобалайық, шығысында логикалық 1 болатын, егер үш кiрiс сигналының екеуi бiрлiк мәндi қабылдаса. Ақиқат таблицасында F шығыс функциясы үшiн, үш кiрiс айнымалы А, В және С кiрiс сигналының сегiз мүмкiн болатын терiмi нөлден жетiге дейiн нөмiрленген. Ол 1-суретте көрсетілген.

Сурет-1.
Әр бiр терiм үшразрядты екiлiк код терiм нөмiрiне сәйкес. Оң жақ бағанада әр бiр терiмге F логикалық функциясының мәндерi көрсетiлген. Ақиқат таблицасы бойынша логикалық функцияға ЖДҚФ (жетiлдiрiлген дизъюнктивтi қалыпты форма) түрiнде (1) теңдiк құруға болады, яғни функцияның бiрлiк терiмiне сай логикалық көбейтiндiлер қосындысы түрiнде:
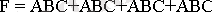 (1)
(1)
Теңдiгi қарапайым логикалық элементтер орындайтын логикалық қосу (дизъюнкция), көбейту (конъюнкция), (2) терiстеу (инверсия) операцияларының көмегiмен жазылған. Бұл 2-суретте көрсетілген.
“Ерекше НЕМЕСЕ” операциясы ЖДҚФ - да мына түрде жазылады
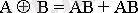 (2)
(2)
Терiм нөмерi

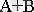
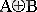
1
2
3
0
1
1
1
0
1
0
0
1
1
1
0
1
1
1
0
0
0
1
1
0

Белгiленуi

ЛИ
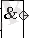
ЛА

ЛЛ

ЛЕ
НЕМЕСЕ
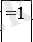
ЛП
Сурет-2.
Логикалық функцияны түрлендiру үшiн келесi Буль алгебрасының заңдары қолданылады:
1) Орын ауыстыру А+В=В+А, АВ=ВА;
2) Жиынтықты (А+В) +С=А+(В+С), (АВ) С=А(ВС) ;
3) Тарату А(В+С) =АВ+АС;
4) Екi жақты

5) Екi жақты терiстеу
ЖДҚФ-да бұрын жазылған үш айнымалының логикалық функциясы мына түрде берiлуi мүмкiн
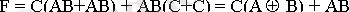 (3)
(3)
(3) теңдiгi бойынша құрылғының функционалдық сұлбасы құрылды. 3-суретте бұл сұлба көрсетілген.
Сурет-3.
Логикалық функцияны Венна диаграммасында кескiндеуге болады. Шеңбердiң iшiндегi аймақ айнымалының тура мәнiне сәйкес, сыртындағы - терiстеуге сәйкес. Венна диаграммасы екi және үш айнымалы бульдiк функцияны минимизациялау үшiн, логикалық теңдiк пен теңсiздiктi дәлелдеу үшiн. Ол 4-суретте көрсетілген.

Сурет-4.

Сурет-5.
Үш және төрт айнымалы логикалық функцияны минимизациялау үшiн Карно картасын қоолданған ыңғайлы. Карно картасы әр бiр тор көздерiнде ақиқат кестесiнiң белгiлi бiр терiмiне сәйкес тiкбұрышты кесте. Картада айнымалының тура мәнiнiң аймағы және әр бiр терiмге логикалық функцияның мәнi тiркейдi (0, 1 немесе Х, егер функция берiлген терiмде анықталмаса) . Бұл 5-суретте көрсетілген.
2 ЛОГИКАЛЫҚ ФУНКЦИЯЛАРДЫ ВЕЙЧ-КАРНО ӘДІСІМЕН МИНИМАЛИЗАЦИЯЛАУ ПРИНЦИПІН ЗЕРТТЕУ
2. 1 Логика функцияларын минимизациялау және оны қарастырғандағы шектеулер
Мүлтіксіз дизъюнктивті қалыпты форма (МДҚФ) жазудың тиімді формасы болмайтынын мысалда көрсетейік:
f(Х
1
, Х
2
) = Х
1
Х
2
 Х
1
Х
2
Х
1
Х
2
 Х
1
Х
2
=Х
1
Х
1
Х
2
=Х
1
 Х
2
Х
1
Х
2
бойынша толық жапсыру негізінде біз жазу қысқарғанын көреміз, өйткені онда байланыс пен әріптер саны аз. Физикалық мағынасы эквивалентті бірақ қарапайым функцияны іске асыратын құрылғыда жабдықтар саны аз болады деген сөз, яғни құрылғы сенімді жұмыс істейді.
Х
2
Х
1
Х
2
бойынша толық жапсыру негізінде біз жазу қысқарғанын көреміз, өйткені онда байланыс пен әріптер саны аз. Физикалық мағынасы эквивалентті бірақ қарапайым функцияны іске асыратын құрылғыда жабдықтар саны аз болады деген сөз, яғни құрылғы сенімді жұмыс істейді.
Сонымен құрылғыны синтездеу есебі ондағы жабдықтарды азайту есебімен толықтырылуы керек. Математикалық көзқарастан бұл есеп минималды ЛАФ-ын құру есебі.
Минималды ЛАФ-ы дегеніміз бастапқы формадағыдан аз әріптер санына тұратын форма.
Егер қандай да бір терімде f а
1
мінін қабылдаса, ал
 а
2
мәнін қабылдаса онда f өзінің а
1
мәнімен
а
2
мәнін қабылдаса онда f өзінің а
1
мәнімен
 функциясының а
2
мәнін жабады деп айтады.
функциясының а
2
мәнін жабады деп айтады.
ЛАФ-ын минимизацилаған кезде бастапқыға қарағанда аз әрпі бар форманы алуға тырысады.
Дизъюнктивті қалыпты формаға қатысты бұл форманы қысқартылған дизъюнктивті қалыпты форма (Қысқ. ДҚФ) деп атайды. ҚДҚФ құрудың мәні оның құрамына бастапқы функцияның бір емес бірнеше бірлігін жабатын бірліктері бар элементар көбейтулер кіреді.
ҚДҚФ - ға кіретін әрбір элементар көбейтінді функцияның тек бір бірлігін жабады.
ҚДҚФ-ны алу тәртібі төмендегідейболуы мүмкін.
1. Бастапқы МДҚФ-ның бірліктерінің конституенттеріне барлық толық емес жабыстыру операцияларын орындау. (n-1) -рангті көбейтінділер шығады. Қалған жапсырылмаған бірліктің конституенттері келешектегі жабыстыруларға қатыса алмайды.
2. Алынған барлық бірлік конституенттерімен көбейтінділерінің жабуын жүргізу. Кейбір бірлік конституенттерінің бөлігі шектеледі.
3. 1) және 2) операцияларын мүмкін болғанша жүргізу.
Мысал 1.
f(Х 1 , Х 2 ) = Х 1 Х 2
Х 1 Х 2
Х 1 Х 2
Егер толық жабыстыру операциясын қолдансақ онда:
f(Х 1 , Х 2 ) = Х 1
Х 1 Х 2
немесе
f(Х 1 , Х 2 ) = Х 1 Х 2
Х 2
яғни, операцияны ары қарай жүргізуге мүмкіндік жоқ.
Енді толық емес жапсыру операциясын қолданайық:
f(Х 1 , Х 2 ) = Х 1
Х 1 Х 2
Х 1 Х 2
Х 1 Х 2
Х 2 = Х 1
Х 2
Х 1 Х 2
Х 1 Х 2
Х 1 Х 2
Х 1 , Х 2 - қарапайым импликанттар
Х 1 Х 2 , Х 1 Х 2 , Х 1 Х 2 - бірліктің коституенттері
Енді жою операциясын жүргізе аламыз:
Х 1 Х 1 -ді жояды, Х 1 Х 2 , Х 1 Х 2
Х 2 Х 2 - ні жояды, Х 1 Х 2 , Х 1 Х 2
Яғни Қысқ. ДҚФ
f(Х
1
, Х
2
) = Х
1
 Х
2
біздің жағдайымызда бұл минималды форма
Х
2
біздің жағдайымызда бұл минималды форма
Толығымен анықталған функцияларды минимизациялау. Нақты құрылғының жұмысы көп жағдайда толығымен анықталмаған функция көмегімен сипатталады, өйткені кіру сигналдарының кейбір комдинациялары берілмейді немесе рұқсат етілмеген болып келеді.
Толық анықталмаған функция аргументтердің кейбір терімдерінде мәндері еркін болатын ауыстырып қосқыш функция болады (яғни, “0” немесе “1”-ге тең) .
f(x
1
, x
2
, . . . x
n
) функциясы аргументтердің “p” терімінде анықталмаған болсын. Онда толық анықталған
 (x
1
, x
2
, . . . x
n
) функциясын f(x
1
, x
2
, . . . x
n
) функциясына эквивалентті деп санаймыз, егер оның мәндері f(x
1
, x
2
, . . . x
n
) анықталған терімдердегі мәндермен сәйкес келсе.
(x
1
, x
2
, . . . x
n
) функциясын f(x
1
, x
2
, . . . x
n
) функциясына эквивалентті деп санаймыз, егер оның мәндері f(x
1
, x
2
, . . . x
n
) анықталған терімдердегі мәндермен сәйкес келсе.
f(x 1 , x 2 , . . . x n ) - ға эквивалентті әр түрлі 2 р функциялары бар екені анық.
f(x
1
, x
2
, . . . x
n
) - ді минимизациялау есебі дегеніміз формасы қарапайым эквивалентті
 (x
1
, x
2
, . . . x
n
) - ді таңдау.
(x
1
, x
2
, . . . x
n
) - ді таңдау.
Толығымен анықталмаған функцияларды Вейч диаграммаларының көмегімен минимизациялау көрнекті және ыңғайлы түрде минималды формаларды іздеп табуға көмектеседі.
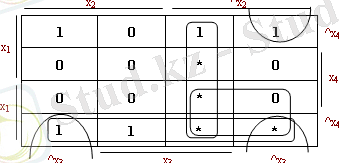
Мысал: f(x 1 x 2 x 3 x 4 ) функциясын қарастырайық та оның минималды формасын табайық. Вейч диаграммасын келесі ережелерге сәйкес толтырайық: бірліктің конституенттеріне сәйкес келетін ұяшықтарға бірлерді қоямыз, жоқ конституенттер үшін - нөлдерді, қалған ұяшықтарға «*» (жұлдызша) - анықталмағандық символын қоямыз.
x 1 ^x 2 x 3 x 4 , ^x 1 ^x 2 x 3 x 4 , ^x 1 ^x 2 x 3 ^x 4 конституенттері үшін ұяшықтарға анықталмағандық символы орнына бірліктерді қойған дұрыс, өйткені ол жағдайда ^x 2 x 3 көбейтіндісімен жабылатын 2 - ші рангті дұрыс конфигурация (Сурет-6) құрылады.
Сурет-6.
Дәл сол сияқты ^x 1 ^x 2 ^x 3 ^x 4 ұяшықтарына бірліктерді қою керек.
Сонымен, f
min
(x
1
x
2
x
3
x
4
) = ^x
2
x
3
 ^x
1
^x
4
^x
1
^x
4
 ^x
3
^x
4
^x
3
^x
4
 ^x
1
^x
2
.
^x
1
^x
2
.
2. 2 Вейч-Карно картасы көмегімен минимизациялау әдісі
Карно картасы бойынша логикалық функция үшiн минимизацияланған теңдеудiң жазылу ережесi:
1) Бiрлiкпен толтырылған блоктар бөлiнедi;
2) блок тiкбұрышты болу керек және 1, 2, 4, 8 тор көздерiнен тұру керек;
3) блоктар мүмкiндiгiнше үлкен болу керек, ал олардың сандары азболуы керек;
4) Сол және оң, сол сияқты үстiңгi және астыңғы карта жолдары көршiлес болып саналады;
5) Бiр тор көз бiрнеше блокқа кiруi мүмкiн;
6) Кесек блокты алу үшiн, функция кез-келген түрде анықталуы мүмкiн (Х тұрған терiмде) ;
7) Бөлiнiп алынған блокты көрсететiн функция логикалық көбейтiндiлер ЛК түрiнде жазылады;
8) Егер оның нақты мәндерiнiң облыстрының блогы теңбе - тең бөлiнбесе, айнымалы ЛК құрамына кiрмейдi;
9) Егер қарастырылып отырған блок оның инверстiк мән облысында жатса, айнымалы инверсиялы ЛК құрамына кiредi;
10) Блоктағы нөлмен толтырылған тор көздерiн топтау кезiнде, сол ереже бойынша логикалық функцияның инверсиялық мәнiн аламыз.
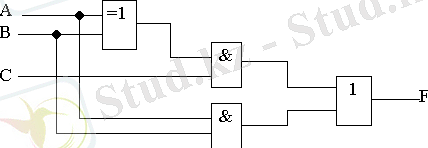
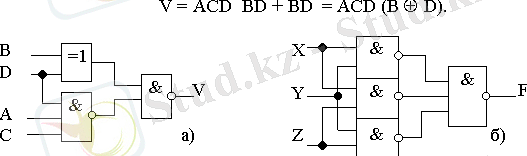
Карно картасы бойынша (Сур. 3. 5, а) V төрт айнымалы логикалық функциясы мына түрде жазылады:
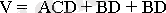
Құрылғыға сай тарату варианты (Сур. 3. 6, а) түрлендiрудi ескередi.
Сурет-7.
Карно картасына сәйкес келетiн (сур . 3. 5, в), үш айнымалы F логикалық функция (оның ақиқат таблицасы сур. 3. 1 бiрдей), жоғарыдағы ереже бойынша мына түрде жазылады:
F = XY + XZ + YZ .
Екi жақтылық формуласын қолданып, ЖӘНЕ -НЕ элементтерiне таратуға ыңғайлы, мына түрге түрлендiруге болады (сур. 3. 6, б) :

Логикалық элементтерде комбинационды сандық құрылғыны жобалау кезiнде, келесi тәртiптi ұсынуға болады:
1) Есеп шарты анықталады (жетiлдiрiлiп отырған құрылғы нақты не iстеу керек екендiгi анықталады, оның жұмыс алгоритмi нақтыланады) ;
2) Берiлген құрылғыға логикалық функция үшiн ақиқат кестесi құрылады;
3) Карно картсының көмегiмен логикалық функцияны минимизациялау жүргiзiледi;
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz