Теориялық механика: материалдық нүкте, санақ жүйелері, координата жүйелері және Лагранж принципі


Теориялық механика пәні, әдістері, бөлімдері.
Теориялық механика-бір макроскопиялық денелердің басқа макроскопиялық денелерге қатысты жеткілікті баяу орын ауыстыру теориясы болып табылады.
Бізге белгілі барлық материалдыы обьектілер жалпы жағдайда қозғалады, яғни өзгереді. Қозғалыстың ең қарапайым формасы ретінде олардың бір-біріне қатысты орын ауыстыруы болып табылады.
Механика-денелердің немесе олардың жеке бөліктерінің бір-біріне қатысты орын ауыстыруынан тұратын материя қозғалысының ең қарапайым формасы туралы ілім.
Қозғалысты сипаттау үшін басқа дегене қатысты берілген дененің ауыстыруын қалай есептейтіндігіміз жайлы анықтайық. Осы мақсатпен таңдап алынған денеміз санақ жүйесін құрайды.
Практикада қозғалысты сипаттау үшін санақ жүйесін құрайтын денелерге коор-та жүйесін байланыстыруға тура келеді. Денелердің кооринаторы оның кеңістіктегі орнын анықтауға мүмкіндік береді. Алайда қозғалыс уақыт бойынша өзгереді.
Кеңістік және уақыт-материяның өмір сүруінің формасы. Сондықтан қозғалысты сипаттау үшін уақытты да есептеу қажет.
Материяның бір сәтке де таластамайтын қозғалысы мен түрленуініғ көрінісі болатын табиғат құбылыстары кеңістікте және уақыт бойынша өтеді. Уақыттың ьелгілі бір сәті мен кеңістігінің белгілі бір нүктелерде болып өтетін кез келген құбылыстың бөлігін оқиға деп атайды. Мысалға: Материалды бөлшектің белгілі бір уақыт сәтінде кеңістіктің белгілі нүктесінде болуы.
Механикадағы негізгі ұғым-материалды нүкте қозғалысын қарастырған кезде өлшемін ескермеуге болатын материалды дене. Бірақ оның массасы дене массасына тең. Денелер және олардың бөліктері геометриялық нүктемен модельденеді. Ал, нүкте әсерлесу кезінде байқалатын массамен қамтамассызданады.
Материалды нүктенің маңызды қасиеті-әрбір уақыт сәтінде оның кеңістіктегі орнын және жылдамдығын анықтауға болады.
Осы жағдайда материалды нүкте қисық сызық бойымен қозғалыс траекториясымен қозғалады. Бірнеше денелерді немесе бір денелердің бөліктерін материалды нүктелермен ауыстыру арқылы, материалды нүктелер жүйесіне келеміз. Материалды нүктелер жүйесіне. Мысалы: нүктелердің ара-қашықтықтары өзгермейтін қатты денелер, тұтас орталар және т. б. жатуы мүмкін. Денелердің қозғалысы, оны құрайтын материалды нүктелер қозғалыстармен алмастырылады.
Механикада кеңістіктің және уақыттың белгілі моделі қолданылады, сонымен атар санақ жүйесі қолданылады. Қозғалыс белгілі бір денелерге қатысты қолданылады, ал денелер санақ жүйесімен алмастырылады. Санақ басы белгіленіп, онымен координаторлар жүйесі байланысады. Координата жүйелерінің ішіндегі ең қарапайым тік бұрышты декарт координаторлар жүйесі. Оны салу үшін бір нүктеде қиылысатын үш өзара перпендикуляр түзулер x, y, z координа өстерін жүргізу жеткілікті.
Санақ жүйесі-қозғалыстағы материалды нүктелерінің кез-келге уақыт сәтінде кеңістіктегі орнын анықтайды. Қатты масштаб және сағат арқылы әрбір уақыт+ сәтінде кейбір санақ жүйесінде материалды нүктенің орнын ч анықтауға болады. Нүкте қозғалыстың кинетикалық теңдеуі сонда.
Механикалық қозғалысты сипаттаудың келесі қадамы материалды нүктенің бір-бірімен әсерлесулерін қарастыру. Механика алыстан бір материалды бөлшек 2 ші материалды бөлшектен белгілі арақашықтықта орналассын, бірінші материалды бөлшек екінші материалды бөлшекке әсер етеді, сонның салдарынан екі бөлшек арасы толтырылған кеңістіктегі ортаның әсерінсіз оның жылдамдығын өзгертеді. әсер кеңістікте лезде беріледі. Бұл әсер күшпен сипатталады. Күш үдеуді туғызады.
Фундаменталды әсерлесулер
Фундаменталды әсерлесу деп-одан ары қарапайым түрге келмейтін әсерлесулерді айтады. Фундаменталды әсерлесулерді сипаттайтын күштерді фундаменталды күштер д. а. Фундаменталды күштер бағынатын заңдарды Фундаменталды заңдар деп атайды.
Бақылауларға қарағанда әсерлесулер өзінің табиғаты жағынан әртүрлі болады. Проавитациялық әсерлер, электр және магнитті әсерлер, көпжақты кезіндегі әсерлер және т. б. Қазіргі кезде 4 Фундаменталды әсерлер белгілі.
- Правитациялық
- Электромагниттік
- Ядролық
- Әлсіз әсерлесулер
Механикадағы белгілі серпімді күштер және үйкеліс күштер фундаменталды күштерге жатпайды. Себебі оларды электромагниттік күштерге жатқызуға болады.
1. Классикалық механикадағы негізгі ұғымдар және принциптер. Классикалық механикадағы моделдері, материалды нүкте.
Дене қозғалысын қарастырған кезде олардың өлшемін өлшеуге болады, берілген есептің шартында өлшемін өлшеуге болатын дене материалдық нүкте д. а. Мысалы: автомобильмен Алматыдан Астанаға қарай жүріп өткен жолды анық кезінде автомобильдің өлшемін бір жолы елемеуге болады. Бір жағдайда математикалық нүкте орнына саналған дене, 2-ші жағдайда аумақты дене ретінде қарастырылуы тиіс. Егер дене өлшемі L қарастырылып отырған Р нүктесіне дейінгі арақашықтықта ч қатысты L<<Ч болса, онда денені математикалық нүкте деп қарастырамыз.
2. Классикалық механикадағы кеңістік және уақыт.
Физикалық кеңістік нүктелердің геометриялық жиынмен модельденеді. Кеңістік үздіксіз, біртекті, изотропты, оның үш өлшемі бар және ол кеңістікте евклид геометриясы орындалады. Кеңістіктің үздіксіздігі жақын жатқан екі нүктенің арасында аз арақашықтықтар болуы мүмкін.
Біртекті-барлық нүктелер тең құқықты
Изотропты-барлық бағыттар тең құқықты
Евлидты-Евлид геометриясы орындалады.
Кеңістіктің масшатабы, күн жиесі 10-16, 10-17 см.
Жалпылама координаталар
Механикада бұны қолдану ыңғайлы. Жалпылама координаталар жүйесінің конфигурациясын толық анықтайтын параметрлер Мысалы: екі бір-бірімен әсерлесетін бөлшектер жүйесі олардың жалпы инерция центрінің 3 декарттық координаталарымен, бөлшектердің арақашықтығымен және бөлшектерді қосатын түзудің орнын анықтайтын 2 бұрышпен сипаттауы мүмкін. Таңдап алынған жалпылама координаталарды әр түрлі индекстері бар бір әріппен q белгілейді. q 1 , q 2 , q 3 кейбір жағдайларда осындай тәсілдің арақашықтығы жалпылама координаталар саны декарттық немесе полярлық координаталар санынан кем(аз) болуы мүмкін. Мысалы: біздің жүйеміз- арақашықтығы α өзгермейтін екі нүктелік массалар болса, онда бұл бөлшектердің аты декарттық координаталар арасында мынадай қатынас
(x 1 -x 2 ) 2 +(y 1 -y 2 ) 2 +(z 1 -z 2 ) 2 =d 2 m 2
(x 2, y 2, z 2)
m 1
(x 1, y 1, z 1)
орын алады. Осы теңдіктен бір координата басқа бес координаталар арқылы байланысады. Сонымен жүйенің конфигурация бес тәуелсіз параметрлерімен толығымен анықталады. Сол себепті бес жалпылама координаталар жеткілікті.
Механикалық күй. Ең аз әсер пирнципі.
(Гамельтон принципі)
1. Механикалаық күй.
Бізде N бөлшектен тұратын жүйе берілсін осы нүктеде кеңістікте орын ауытқу үшін 3N координаталар қажет болады. Осы жүйенің жалпы жағдайда орын ауытқу үшін қажетті тәуелсіз сан сол жүйенің еркіндік дәрежесі деп аталады.
Z Бұл шамалар міндетті түрде декартты коорди-
ната болуы қажет емес. Есептің шартына қарай ол координаталар басқа координаталар болуы
мүмкін. Мысалы: q 1 , q 2 , q 3 шамалары берілсін. Бұл шамалар жүйенің орынын сипаттайтын болса,
онда бұл шаманы жалпылама координаталар деп
атайды. Ал осы шаманы уақыт бойынша туынды-
лары, яғни q 1 , q 2 , q 3
- осы координаталардан уақыт бойынша туынды.


q i - шамалары жалпылама жылдамдықтар.

Жүйенің механикалық күйін толық сипаттау үшін жалпылама координаталар жеткіліксіз болады. Жүйенің күйін толық сипаттау үшін координаталардан басқа ол жүйені жылдамдық белгілі болуы қажет. Сонымен материалдық жағынан белгілі бір уақыт сәтінде жүйенің барлық жалпылама координаталары және жылдамдығы координаталардың және жылдамдығымен байланысты қозғалыс теңдеуі деп атайды. Координаталарға байланысты q(t) бұл теңдеулер екінші ретті диференциалдық теңдеулер. Ол теңдеуді интегралды осы q(t) функциясын анықтауға болады.
2. Ең аз әсер принципі (Гамельтон принципі) .
Механикалық жүйе қозғалыс заңының жалпы анықтамасы ең аз әсер принципі арқылы беріледі. Осы принціпке сәйкес әрбір механикалық жүйе мынадай функциямен L(q
1
q
2
…q
5
q
1
q
2
q
5
t) сипатталады. Бұл функцияның қысқаша түрі
 t=t
1
уақыт моментінде және t=t
2
уақыт моментінде жүйе q(1) және q(2) координаталармен сипаттайтын болсын. Сонда осы екі орындарында жүйе қозғалған кезде мына интеграл
t=t
1
уақыт моментінде және t=t
2
уақыт моментінде жүйе q(1) және q(2) координаталармен сипаттайтын болсын. Сонда осы екі орындарында жүйе қозғалған кезде мына интеграл

мүмкін болатын ең аз мән қабылдайды. Осы тұжырымды ең аз әсер О принципі немесе Гамельтон принципі деп атайды. Мына
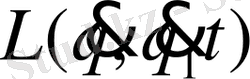 функциясын Лагранж функциясы деп атайды. Ал мына бірінші интегралды әсер деп атайды.
функциясын Лагранж функциясы деп атайды. Ал мына бірінші интегралды әсер деп атайды.
3. Жүйе қозғалысының дифференциялды теңдеуі.
Бізге жүйе берілсін және ол жүйенің еркіндік дәрежесі бірге тең болсын сонда қозғалыстың дифференциялдық теңдеуі
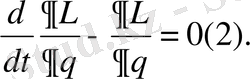
Егер жүйенің еркіндік дәрежесі бірнеше болса, онда қозғалыс теңдеуі мынадай болады.
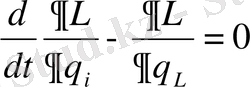 i= (1, 2, …5)
i= (1, 2, …5)
Осы үшінші теңдеу механикада Лагранж теңдеуі деп аталады.
Егер берілген механикалық жүйенің Лагранж функциясы белгілі болса онда (3) теңдеу үдеудің, жылдамдықтың және координаталардың байланысын көрсетеді. Яғни жүйенің қозғалыс теңдеуін береді. Бізге инерциялы санақ жүйесі берілсін осы жүйе бөлшек еркін қозғалысы болсын сол бөлшектің Лагранж функциясының түрін анықтайық. Кеңістік және уақыт біртекті болса онда бұл функция тек қана жылдамдықтың функциясы болып табылады.
Егер кеңістік изотропты болса, онды Лагранж функциясы жылдщамдықтың обсалют шамасының функциясы болып табылады.
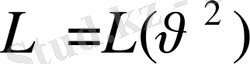 осы функцияның түрін анықтау үшін салыстырмалы принципын қолданайық. Егер К инерциялды жүйесі К’ инерциялды жүйеге қарағанда өте аз ε жылдамдығы қозғалса онда салыстырмалы принціпке сәйкес
осы функцияның түрін анықтау үшін салыстырмалы принципын қолданайық. Егер К инерциялды жүйесі К’ инерциялды жүйеге қарағанда өте аз ε жылдамдығы қозғалса онда салыстырмалы принціпке сәйкес
 қозғалыс теңдеуінің түрі барлық инерциялы жүйелері бірдей болғандықтан
қозғалыс теңдеуінің түрі барлық инерциялы жүйелері бірдей болғандықтан
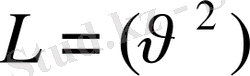 Лагранж функциясы мынадай түрге келуі қажет
Лагранж функциясы мынадай түрге келуі қажет
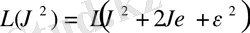 осы өрнекті ε дәрежелері бойынша қатарға жіктеп мынадай қатынасты аламыз.
осы өрнекті ε дәрежелері бойынша қатарға жіктеп мынадай қатынасты аламыз.
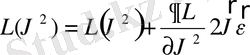 осы өрнектегі 2-ші мүше уақыт бойынша толық туынды бола алады егер ол мүше
осы өрнектегі 2-ші мүше уақыт бойынша толық туынды бола алады егер ол мүше
 сызықтары байланысты болады. Сондықтан мына шама
сызықтары байланысты болады. Сондықтан мына шама
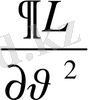 жылдамдыққа байланысты емес, яғни ол жылдамдықтың квадратына тура пропорционал болады.
жылдамдыққа байланысты емес, яғни ол жылдамдықтың квадратына тура пропорционал болады.
 бұл коэффициентін
бұл коэффициентін
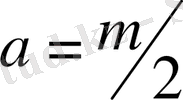 деп алып еркін қозғалысын бөлшектің Лагранж функциясы мынаған тең болады.
деп алып еркін қозғалысын бөлшектің Лагранж функциясы мынаған тең болады.
 .
.
3. Галилейдің салыстырмалы принципі
1. Галилейдің түрлендірулері
Қозғалынатын жүйеге қатысты дененің қозғалысын салыстырмалы деп атайды. Қозғалатын жүйенің қозғалмайтын жүйеге қатысты қозғалысын ауыстыру қозғалысы деп атайды. Бізге қозғалмайтын санақ жүйесі берілсін ол санақ жүйесі инерциялды болады. Ньютонның біріні заңы орындалатын санақ жүйесін инерциялды деп атайды.
1. Сфералық координата жүйесі - өрнектің декарттық координата жүйесімен байланысты x, y, z, φ, θ x=x(r, φ, θ), y=y(r, φ, θ), z=z(r, φ, θ), r=r(x, y, z), φ=φ(x, y, z), θ=θ(x, y, z) . Кез келген механикалық есепті шешу үшін көбінесе координаталар жүйесін таңдап алады.
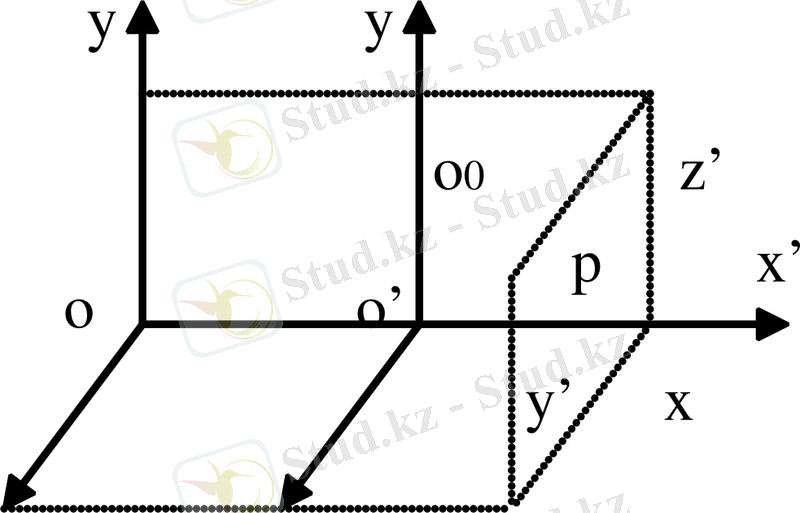 Негізінде есептің өзіне симметриялық болатын
Негізінде есептің өзіне симметриялық болатын
оординаталар жүйесін таңдап алғанда есеп оңай шешім табады. Сондықтан орталық алаңда қозғалыс үшін таңдамалысы полярлық координаталар жүйесі болып табылады. Біз атомның планета аралық модельін қарастырғанда, энергияның сақталу заңымен қозғалыс санының
моментінен пайдаланамыз. Бұл бақылайға дайындық ретінде біщ энергия жыне полярлық координат үшін теңдеу жазамыз. Жазықтықтағы нүктенің жағдайы екі полярлық координатамен r және φ мен анықталады, олар декарттық қозғалыспен қатынасады.
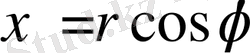
(1)
болады. Декарттық координаталар жүйесінде кинетикалық энергия былай өрнектеледі.
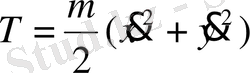 (2)
(2)
Бір-ақ (1) өрнектен шығу керек болғаны.
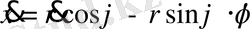 ,
,
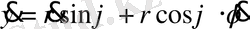
(3) -ші теңдеуді (2) ге қойып нәтижесінде алатынымыз
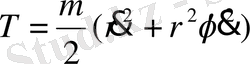
Бұл кинетик энергияның жазықтықтағы полярлы координаттары системасындағы теңдеуі болып табылады. (1) ші теңдеумен (3) ші теңдеуді қосып нәтижесінде алатынымыз
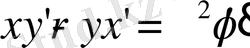
Кеңістіктегі Р нүктесінің сфералық, полярлық координатасы үшін қызмет ететін радиус вектор r полюстік арақашықтық υ алыстық (ұзындық φ) . Бұл қандайда бір алғашқы меридианды бастап саналады. Декарттық және полярлық координаттар жүйесінің сәйкестігі сүретте көрініп тұр x=rsinυcosφ, y=rsinυsinφ.
бұдан r = r cosφ
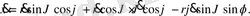
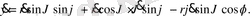
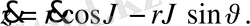
Бұл теңдеуді кеңістіктегі декарттық координаталар жүйесіндегі кинетикалық энергтяның теңдеуіне қатысып нәтижесінде
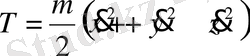
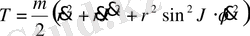
Сфералық, полярлық координаттар жүйесіндегі кинетикалық энергия.
Галилейдің салыстырмалы принципі
Бізге екі санақ жүйесі берілсін.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz