Матрицалар

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 11 бет
Таңдаулыға:

Жоспар

Анықтауыштар
Матрицалар теориясының элементтері

Сызықты теңдеулер жүйесі

Пайдаланылған әдебиеттер

1. Анықтауыштар

1. mхn-саннан жасалған мына түрдегi

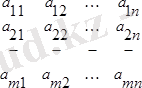
тiк бұрышты таблицаны mхn өлшемдi матрица дейдi. Таблицаның көлденең қатарларын матрицаның - жолдары, тiк қатарларын - бағандары дейдi. Матрица жасалған cандары матрицаның элементтерi делiнедi:

немесе

немесе қысқаша:
(1. 1)

Әр элементке тиiстi екi индекстiң бiрiншiсi ол элементтiң нешiншi жолда, екiншi индекс нешiншi бағанда тұрғанын бiлдiредi.
Жолының саны мен бағанының саны тең матрицалар квадрат матрица делiнедi. Квадрат матрицаның бiр ерекшелiгi оның анықтауышының болатындығы.
nхn өлшемдi квадрат матрицаны n-реттi анықтауыш деп, оның жолдары мен бағандарының әрқайсысынан бiр-бiрден алынған n элементтің көбейтiндiлерiнен тұратын n! (факториал) қосылғыштың (мүшенiң) алгебралық қосындысын айтады. Ол қосылғыштардың таңбасы оған енетiн элементтердiң бiрiншi индекстерi натурал тәртiпте орналасқан жағдайда, екiншi индекстерi жұп инверсия жасаса - оң, тақ инверсия жасаса - терiс болады.
Анықтауыш былайша белгiленедi:

(1. 2)

1-мысал. Алтыншы реттi анықтауыш берiлген. Ол анықтауыш неше қосылғыштың қосындысынан тұрады, әр қосылғышқа неше элементтен енедi, бас және көмекшi диагоналда индекстерi қандай элементтерден тұрады?
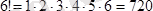
Шешуi. Алтыншы реттi анықтауыш 6 элементтен қанша алмастыру жасауға мүмкiн болса, сонша қосылғыштардың қосындысына тең болады, ал 6 элементтен 6 факториал, алмастыру жасауға болады. Бұл 720 қосылғыштың әрқайсысына анықтауыштың әр жолының (сондай-ақ бағанының) тек бiр элементi енетiндiктен, ол қосылғыштар 6 элементтiң көбейтiндiсінен тұрады.
Бас диагонал a ₁₁ , a ₂₂ , a ₃₃ , a ₄₄ , a ₅₅ , a ₆₆ элементтерден, екiншi диагонал a ₆₁ , a ₅₂ , a ₄₃ , a ₃₄ , a ₂₅ , a ₁₆ элементтерден тұрады.
2- мысал . Бесiншi реттi анықтауыштың a ₃₄ , a ₂₁ , a ₁₃ , a ₅₅ , a ₄ ₂ , элементтерiнiң көбейтiндiсiнен тұратын мүшенiң (қосылғыштың) таңбасы қандай болады?
Шешу i. Таңбасын анықтау үшiн бұл мүшеге енетiн элементтердiң бірінші индекстерi нормаль түрге (яғни натурал тәртiпке) келетiндей етiп оларды орналастырамыз:

a ₁₃ a ₂₁ a ₃₄ a ₄₂ a ₅₅

Сонда екінші индекстер 3 1 4 2 3 алмастыруын жасайды Бұл алмастыруда натурал орналасу тәртiбiн 3 екi рет бұзған (өзiнен кiшi 1 мен 2-нiң алдына шығып кеткен), яғни 2 инверсия жасайды, 1 саны 0 инверсия жасайды, 4 саны 1 инверсия жасайды, 2 мен 5 сандары 0 инверсиядан жасайды. Сонда барлығы 3 инверсия жасалған, яғни инверсия саны тақ болып шықты. Сондықтан бұл элементтерден тұратын мүшенiң таңбасы терiс болады.
3-мысал.

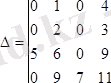
анықтауышының мәнiн анықтауыштың анықтамасына сүйенiп табыңдар.
Шешуi. Бұл анықтауыш төртiншi реттi, сондықтан ол 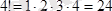қосылғыштың (мүшенiң) алгебралық қосындысынан тұрады және ол қосылғыштардың әрқайсысы 4 элементтiң (санның) көбейтiндiсiне тең болады.
Бiрiншi жолдағы 4 элементтiң екеуi 0, сондықтан олар енетiн мүшелер нөлге тең болады. Демек, нөл енбейтiн қосылғыштардың қосындысын тапсақ жеткiлiктi.
Бiрiншi жолдан 1-дi аламыз, ол екiншi бағанда тұр: a ₁₂ =1. Сондықтан бұл мүшеге ендi бірінші жол мен екінші бағаннан элемент алуға болмайды. Демек екінші жолдан тек 3-тi (a ₂₄ =3) аламыз, үшiншi жолдан a ₃₁ =5, төртінші жолдан a ₄₃ =7-нi аламыз.
Сонымен iздеген 24 қосылғыштың бiрi болады.
Егер бірінші жолдан a ₁₄ =4 алсақ, онда екінші жолдан тек a ₂₂ =2-нi, үшінші жолдан a ₃₁ =5, төртінші жолдан a ₄₃ =7-нi алуымыз керек, демек 24 қосылғыштың екiншiсi болады. Қалған қосылғыштың барлығы нөл болып кетедi. Ендi табылған нөлге тең емес екi мүшенiң таңбасын анықтайық.
1-жағдайда a ₁₂ , a ₂₄ , a ₃₁ , a ₄₃ элементтердi алдық, екiншi жағдайда a ₁₄ , a ₂₂ , a ₃₁ , a ₄₃ элементтерi алынады. Бұлардың элементтерiнен бiрiншi индекстерiн натурал тәртiпте орналастырсақ a ₁₂ , a ₂₄ , a ₃₁ , a ₄₃ және a ₁₄ , a ₂₂ , a ₃₁ , a ₄₃ болады да, екiншi индекстерi 2 4 1 3 және 4 2 1 3 алмыстыруларын жасар едi. Мұның бiрiншiсiнiң инверсиясы 1+2+0+0=3, екiншiсiнiң инверсиясы 3+1+0+0=4 болады. Демек 105-ке тең мүше таңбасы минус, 280-ге тең мүшенiң таңбасы оң болады.
Сонымен берiлген анықтауыштың мәнi

D=-105+280=175

болады.
Үшiншi реттi анықтауыш деп мына санды:

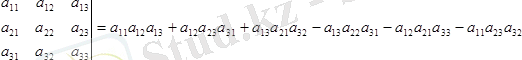, (1. 3)

екiншi реттi анықтауыш деп мына санды:

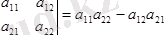(1. 4)
айтамыз.
Үшінші реттi анықтауышты есептеуге арналған (1. 3) формуланы Саррюс әдісі деп атаймыз. Ол 3!=1×2×3=6 мүшенiң қосындысына тең және әр мүшеге әр жолдан, әр бағанадан тек бiр элементтен енедi.
4-мысал .

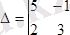
екiншi реттi және

үшiншi реттi анықтауыштың мәндерiн табайық.
Шешуi.

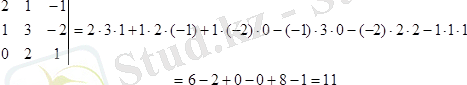
2. n-реттi анықтауыштың a _ij элементi тұрған i-жол мен j-бағанды сызып тастағаннан қалған (n-1) реттi анықтауышты ол элементтiң миноры, ал (-1) ^i+j таңбамeн алынған минорды алгебралық толықтауышы дейдi.
Элемент a _ij -дың минорын M _ij , алгебралық толықтауышын A _ij - мен белгiлесек:

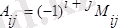(1. 5)

болып шығады.
Мысалы, үшінші реттi (1. 3) анықтауыштың a ₂₁ , a ₃₃ элементтерiнiң минорлары M ₂₁ , M ₃₃ мен алгебралық толықтауыштары A ₂₁ , A ₃₃ мынадай болады:

.

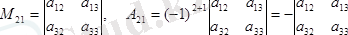
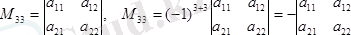5-мысал.

үшiншi реттi анықтауыштың бiрiншi бағанында тұрған элементтердiң миноры мен алгебралық толықтауыштарын табыңдар.
Шешуi. a ₁₁ =2 тұрған бірінші жол мен бірінші бағанды сызып тастасақ, қалғандары оның миноры болады:

;

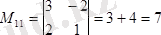Ал, алгебралық толықтауыш:

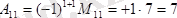
болады. A ₂₁ =1 тұрған екінші жол мен бірінші бағанды сызып тастаса:

,

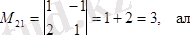
M ₃₁ = 0 тұрған үшінші жол мен бірінші бағанды сызып тастасақ:

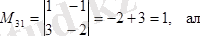
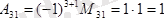
3. Анықтауыштың негiзгi қасиеттерi мыналар:
1 ⁰ . Анықтауыштың мәнi оның жолдары мен сәйкес бағандарының орнын ауыстырғаннан өзгермейдi. Сондықтан анықтауыштың жолы туралы қандай да бiр тұжырым дұрыс болса, ол тұжырым баған үшiн де дұрыс болады.
2 ⁰ . Анықтауыштың кез келген екi жолының орнын ауыстырғаннан анықтауыштын мәнi өзгермейдi, таңбасы керi ауысады.
3 ⁰ . Анықтауыштың бiр жолының барлық элементтерi тең болса, онда анықтауыштың мәнi нөлге тең болады.
4 ⁰ . Анықтауыштың бiр жолының немесе бір бағанының барлық элементтерiнiң ортық көбейткiшi болса, онда оны көбейткіш етіп анықтауыштың таңбасының сыртына шығаруға болады.
5 ⁰ . Анықтауыштың екi жолының сәйкес элементтерi пропорционал болса, онда анықтауыштың мәнi нөлге тең болады.
6 ⁰ . Анықтауыштың бiр жолының элементтерiнiң әрқайсысы екi санның қосындысынан тұрса, онда оны екi анықтауыштың қосындысы ретiнде жазуға болады.
Мысалы:

= + .

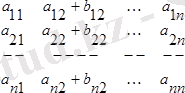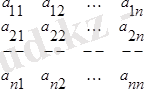7 ⁰ . Анықтауыштың бiр жолының барлық элементтерiн нөлден өзге бiр санға көбейтiп, басқа жолының сәйкес элементтерiне қосса, одан анықтауыш мәнi өзгермейдi.
8 ⁰ . Анықтауыштың бiр жолының барлық элементтерi нөлге тең болса, онда анықтауыштың мәнi де нөлге тең болады.
9 ⁰ . Анықтауыштың бiр жолының элементтерi мен ол элементтердiң алгебралық толықтауыштарының көбейтiндiсiнiң қосындысы анықтауыштың мәнiне тең болады.
10 ⁰ . Анықтауыштың бiр жолының бiр элементiнен басқа элементтерiнiң барлығы нөл болса, онда ол анықтауыштың реттiлiгiн бiрге кемiтуге болады және сол элементтерi оның алгебралық толықтауышының көбейтiндiсiне тең болады.
11 ⁰ . Анықтауыштың бiр жолының элементтерi мен басқа жолының сәйкес элементтерiнiң алгебралық толықтауыштарының көбейтiндiсiнiң қосындысы нөлге тең болады.
6-мысал.

анықтауыштың мәнiн анықтауыш қасиеттерiне сүйенiп табыңдар.
Шешуi. Бұл анықтауыштың мәнiн 4-мысалда Саррюс әдiсiмен тапқанбыз. Ендi оның мәнiн анықтауыш қасиеттерiне сүйенiп табайық.
а) 9 ⁰ қасиетке сүйенiп, анықтауышты бірінші бағанның элементтерi бойынша жiктейiк:

б) 10 ⁰ қасиетке сүйенiп, анықтауыштың реттiлiгiн бiрге кемiту жолымен табу үшiн, 7 ⁰ қасиет бойынша екінші жолдың элементтерiн 2-ге көбейтiп, бірінші жолдың сәйкес элементтерiнен алып тастайық:

= .

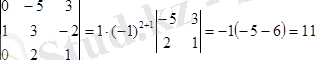7-мысал.

төртiншi реттi анықтауыштың мәнiн табыңдар.
Шешуi. 7 ⁰ қасиетке сүйенiп, бірінші жолдың элементтерiн 3-ке көбейтiп, үшінші жолдың сәйкес элементтерiнен шегерсек:

.

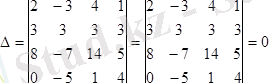Соңғы анықтауыш нөлге тең. Себебi оның екi жолының сәйкес элементтерi пропорционал, ондай анықтауыштар 5 ⁰ қасиет бойынша нөлге тең болады. Демек, берiлген анықтауыш та нөлге тең.
8-мысал.

бесiншi реттi анықтауыштың мәнiн табыңдар.
Шешу i. Анықтауыштың 6 ⁰ қасиетiне сүйенiп, берiлген анықтауышты екi анықтауыштың қосындысы ретiнде жазайық. (1-баған элементтерiн 2=1+1, 1=1+0, 1=1+0, 1=1+0, 1=1+0 деп жазуға болады) :

http://www.yki.kz/images/stories/lecture/algebralec2.files/image038.png

Бұл анықтауыштардың бірінші жолының элементтерiн қалған жолдардың сәйкес элементтерiнен шегеремiз, ал екiншiсiн 10 ⁰ қасиет бойынша жазамыз:

Бiрiншi анықтауышта диагоналдың бiр жағында жатқан элементтерiнiң барлығы нөлге тең. Сондықтан ол анықтауыштың мәнi диагоналда тұрған элементтерiнiң көбейтiндiсiне тең болады. Ал, екiншi анықтауышты тағы да екi анықтауыштың қосындысына жiктеп жазамыз:

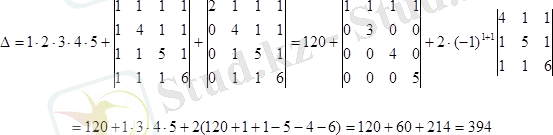
http://www.yki.kz/images/stories/lecture/algebralec2.files/image039.png

9-мысал.

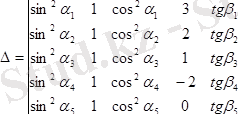
анықтауышының мәнiн табыңдар.
Шешуi. Анықтауыштың екінші баған элементтерiн 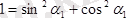түрiнде жазып, одан соң 6 ⁰ қасиет бойынша жiктесек:

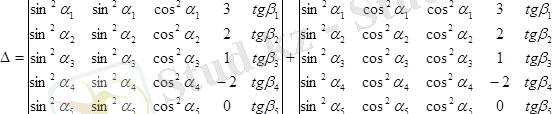
болар едi. Бұл анықтауыштың екеуiнде де элементтерi өзара тең бағандар бар, сондықтан екi анықтауыш та 3 ⁰ қасиет бойынша нөлге тең болады. Демек, берiлген анықтауыштың мәнi нөлге тең болады екен.
4. Реттiлiгi бiрдей екi анықтауышты өзара көбейтуге болады, нәтижеде реттiлiгi соларға тең болатын анықтауыш шығады.
n-реттi D ₁ және D ₂ екi анықтауыш берiлсiн, олардың көбейтiндiсi D ₁ -D ₂ =D десек:

, ,

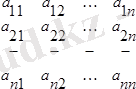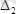
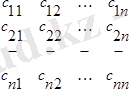
Анықтауыштарды өзара көбейту былайша орындалады: D ₁ - дің бірінші жолының элементтерiн D ₂ -нiң бірінші бағанының сәйкес элементтерiне көбейтiп қосып, бірінші жолдың элементi етiп жазады, ол С ₁₁ болады:

C ₁₁ = a ₁₁ b ₁₁ + a ₁₂ b ₂₁ +…+ a _n ₁ b _n ₁

Одан сан D ₁ деп сол бірінші жолының элементтерiнiң D ₂ -нiң екінші бағанының сәйкес элементтерiне көбейтiп қосып, бірінші жолдың екінші элементi етiп жазады, ол С ₁₂ болады:

C ₁₂ =a ₁₁ b ₁₂ +a ₁₂ b ₂₂ +…+a _1n b _1n

Осы бiр жолдың элементтерiн 3-, 4, -, … ең соңында n бағанға көбейтiп қосып, С ₁₃ , С ₁₄ , …, С _1n -дi табады.
Содан соң D ₁ -дегi екінші жолының элементтерiн D ₂ -нiң 1-, 2-, …, n бағандарының элементтерiне көбейтiп С ₂₁ , С ₃₃ , …, С _2n -дi табады. Осы процестi соза отырып, D ₁ -дегi n-жолының элементтерiн D ₂ - нiң бағандарына көбейтiп қосу арқылы С _n1 , C _n2 , …, C _nn элементтерi табылады.
Сонда D- ның С _ij элементi мына формуламен табылады:

C _ij = a _i ₁ b ₁ _j + a _i ₂ b ₂ _j +…+ a _in b _nj

10-мысал. Төмендегi 2-реттi анықтауыштарды көбейтiңдер:

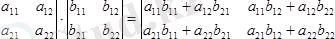
11-мысал. Төмендегi 3-реттi анықтауыштарды көбейтiңдер:

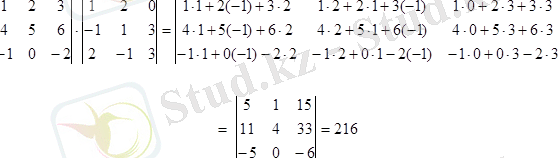
12-мысал. Төмендегi екi 2-реттi анықтауышты төрт жолмен көбейтiңдер.
Шешуi:

а)

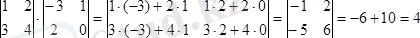
б)

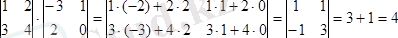
в)

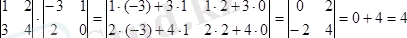
г)

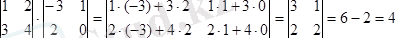
Кейде анықтауыштың мәнiн табу үшiн оны басқа анықтауышқа көбейту пайдалы болады.
13-мысал. Мына анықтауыштың

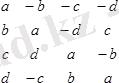
мәнiн табу үшiн оны өзiне-өзiн көбейткен жөн:

14-мысал.

n-реттi анықтауышты есептеңдер.
Шешуi. Бұл анықтауыштың бас диагоналында a элементi, қалған орындарда b элемент тұр.
Мұндай анықтауышты есептеу үшiн 1-жол элементтерiн қалған жолдардың сәйкес элементтерiнен шегередi:

Ендi барлық бағанды 1-баған элементтерiне қосады:

;

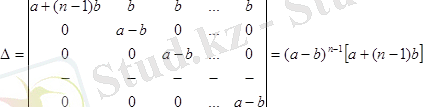2. Матрица

Матрица (нем. Matrіse , лат. matrіx - аналық) -

математикада кез келген жиынның элементтерінен құрылған және m жол мен n бағаннан тұратын тік төртбұрышты А кестесі. Матрицаны түзетін нысандар оның элементтері деп аталады. Матрицаның элементтері оның жолдары немесе бағаналарының бойымен орналасады. Матрицаның элементтері аіj түрінде қос индекспен өрнектеледі, мұндағы бірінші индекс і - Матрицаның аіj элементі орналасқан жолының нөмірін , екінші индекс j - оның аіj элементі орналасқан бағананың нөмірін көрсетеді. Матрица символдық түрде не дөңгелек жақша , не қос тік сызық арқылы өрнектеледі. Мұндай матрицаны (m n) өлшемді тікбұрышты матрица деп, ал егер m=n болса, квадрат матрица деп, n санын оның реті деп атайды.

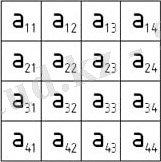
Матрицаны қысқаша былай белгілейді: (аіj) .
Жолдарының саны мен бағаналары санының бірі немесе екеуі де шексіз болатын матрицаны шексіз матрица деп түсінеміз. Бір ғана жолдан немесе бір ғана бағанадан тұратын матрицалар да болады.
аіі диагональ элементтері ғана нөлден өзгеше болатын квадрат матрицаны диагональ М. деп аталып, dіag(а1 … аn) таңбасымен белгіленеді. Диагональ матрицаның барлық элементтері (аі=1) болса, бірлік матрица деп аталады. Егер барлық (аі=а) болса, онда скаляр матрица шығады. Барлық элементтері нөлге тең М. нөлдік М. деп аталады.
Жолдары мен бағаналарын ауыстыру арқылы алынған матрица транспозицияланған матрица деп аталып, А немесе АТ арқылы белгіленеді. Егер матрицаның элементтерін комплекс түйіндеске ауыстырсақ, онда комплекс түйіндес матрицасы шығады. Егер А транспозицияланған матрица элементтерін комплекс түйіндеске ауыстырсақ, онда А матрицамен түйіндес болатын А* матрицасы шығады.
Квадрат матрицаның анықтауышы A немесе det A деп белгіленеді.

Үшбұрыштығы матрица

Матрицаларға амалдар қолдану. Матрицаға қосу, көбейту алгебралық амалдар қолданылады. А тікбұрышты (m n) матрицасының санына көбейтіндісі деп барлық аіj элементтерін санына көбейткенде шығатын матрицаны айтады: . Бұл амалдар: А+В=В+А, А+(В+С) =(А+В) +С, ( + ) А= = А+ А, (А+В) = А+ В, ( А) =( ) А қасиеттерін қанағаттандырады. Матрицаның қосындысы оның құрау-шыларының қосындысына тең. Матрицаны көбейту амалы 1-көбейткіш бағаналарының саны 2-көбейткіш жолдарының санына тең тік бұрышты матрицалар үшін ғана орындалады. (m p) өлшемді А матрицаның (p n) өлшемді В матрицасына көбейтіндісі элементтері сіj=аі1b1j+аі2b2j+ +…+аіpbpj, і=1, …, m, j=1, …, n болатын (m n) өлшемді C матрицасы болып табылады. Матрицаларға енгізілген үш амал сандарға қолданылатын амалға жақын. АВ және ВА матрицаларының көбейтіндісі бірінші ретті квадрат М. үшін ғана анықталады және көбейткіштердің ретіне де байланысты, яғни АВ=ВА орындалмай қалуы да мүмкін. Егер АВ=ВА болса, онда А және В матрицалары ауыспалы деп аталады. Әрбір көбейткіші нөлден өзгеше болса да, екі матрицаның көбейтіндісі нөлдік матрицаға тең болуы мүмкін. Сонда М. үшін (АВ) =А В, , (AB) *= =В*А* ережелері орындалады.
Екі квадрат матрицаның көбейтіндісінің анықтауышы көбейтілетін матрицалар анықтауышының көбейтіндісіне тең. Егер анықтауышы нөлге тең болмаса , онда А=(аіj) квадрат матрицасы өзгеше емес деп, ал кері жағдайда ерекше матрица деп аталады. Кез келген өзгеше емес матрицаның АА-1=Е теңдеуімен анықталатын бір ғана кері А-1 матрицасы болады. Бірдей n ретті А және В квадрат матрицалары ұқсас матрицалар деп аталады.
К өрісіндегі коэффициенттері а0, а1, …, an болатын n дәрежелі кез келген Pn(t) =а0tn+ +а1tn-1+…+аn-1t+аn көпмүшесі Х квадрат М-нан Pn(Х) = а0Хn+а1Хn-1+…+аn-1 Х+аnЕ функциясын анықтайды. Егер f(t) аналит. функциясы барлық комплекс жазықтықта жинақталатын қатары арқылы анықталатын болса, онда функция М-нан қарастырылады. Бұл қатар кез келген квадрат М. үшін жинақты болады. М. сызықтық алгебрада, векторлық кеңістікте сызықтық бейнелеуді зерттегенде, сызықтық және квадраттық тұлғаларда, сызықтық теңдеулер системасында қолданылады. М-ны матем. анализде дифференц. жүйесіне, ықтималдықтар теориясында, кванттық механикада, т. б. пайдаланады. [1]