Санау жүйелері және негіздер арасындағы түрлендіру әдістері


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:
САНАУ ЖҮЙЕСІ
Санау жүйесі. Код
Санау жүйесі дегеніміз - сандарды цифрлар, арнайы символдар арқылы жазу және оларды оқу ережелері мен тәсілдерінің келісілген жиынтығы. Санау жүйелерінің позициялық және позициялық емес болып бөлінетін екі түрі бар.
Компьютер үшін пайдаланылатын код - 0 мен 1-ден тұратын тізбек. 0 мен 1 - екілік санау жүйесінің цифрлары. Информатикада код түзетін мұндай цифрлар бит деп аталады (binary digit-екілік сан) Екілік санау жүйесінің сандары ондық сандар сияқты бір разрядты, екі разрядты не көп разрядты болып келуі мүмкін. ‡шінші және одан жоғарғы компьютерлерде бір символды кодтау үшін 8 разрядты екілік код пайдаланылады. Мысалы, 11000101.
Код - ақпаратты ұсыну үшін пайдаланылатын шартты белгілеулер жинағы, символдардың және оларды түсіндірудің бірмәнді ережелерінің жүйесі.
Жадтың көлемі байтпен өлшенеді. Бір байт сегіз биттен тұрады. Бит деп 0 мен 1 мәндерінің біреуін ғана қабылдай алатын ақпарат өлшемінің ең кіші бірлігін айтады. Сонымен, бір байт көлемдегі жадқа бір символ сақтауға болады. Қазіргі кезде компьютердің жадының көлемі миллиондаған байтқа жетеді, сондықтан оны килобайт, мегобайт, гигобайт арқылы қысқаша өрнектеген ыңғайлы:
1 Гбайт = 1024 Мбайт
1Мбайт = 1024 Кбайт
1Кбайт = 1024 байт
Қазіргі күнде, бүкіл жер шарында жасап жатқан барлық халықтардың қолданатын сандары 0-ден 9-ға дейінгі болған цифрлар, яғни ондық санақ жүйесіндегі сандар және олардың комбинациялары. Бірақ мұндай жағдай бірнеше мыңдаған жылдар өткен соң ғана қалыптасқан. Математикалық тұрғыдан қарағанда ондық санақ жүйесінің басқа санақ жүйелерінен әлеуметтік басымдылығы (ерекшелігі) жоқ. Адамдардың екі қолында 10 саусақтары барлығы, олардың ежелден бірден онға дейін санақтарды жүргізуіне мүмккіндік туғызған. Он ондық үшінші разряд бірлігін құрайды және т. с. с. Сөйтіп, қол саусақтарымен санау қазіргі күндегі ондық жүйесімен санаудың және есептеудің негізі болған.
Адамзат өз тарихында әртүрлі есептеу және санау жұмыстарын ондық санау жүйесінен басқа да санақ жүйелерін пайдаланған. Мысалы, он екілік санақ жүйесі көп жерлерде кең түрде қолданылған. Оның келіп шығуына да адам қолындағы бес саусақтағы бақай (башпай) сүйектерінің саны 12 болуы себепші болған соң 12 саны кейінгі разряд бірлігі ретінде қабылданған. Қазіргі уақытта сервистегі ыдыстар санының 12 немесе 6 дана, 1фут = 12 дюйм 1 шиллинг = 12 пенс болуы, сол 12 санақ жүйесінің қолданылғандығынан келіп шыққан және осы күнге дейін жетіп келген.
Ертедегі дамыған және гүлденген Вавилонда алпыстық санақ жүйесі қолданылған. Неліктен осы санақ жүйесі қолданылғандығы жөнінде пікірлер бір-біріне қайшы келеді. Солардың ішіндегі шындыққа жақын келетін гипотеза мынадай: Екі тайпа болып, олардың бірі алтылық санақ жүйесін, ал екіншісі ондық санақ жүйесін пайдаланған. Сол екі тайпаның бірігуінің нәтижесінде, олардың екеуін де қанағаттандырған алпыстық санақ жүйесі пайда болған. Басқа гипотеза бойынша, Вавилондықтар бір жылда 360 тәулік бар деп есептеген және ол 60 санымен байланыстырылған. Алпыстық санақ жүйесі де онекілік санақ жүйесі сияқты осы күндері де қолданылады. Оған мысал ретінде 1 сағат = 60 минут, 1минут = 60 секунд және т. б. келтіруге болады.
Сандардың аталу және жазылу тәсілдерінің жиынтығы-санау жүйесі деп аталады. Сандарды жазғанда қолданылатын шартты белгілер-цифрлар деп аталады. Ал санның жазылуын әріп-цифрлардан тұратын цифрлық алфавитпен жазылған сөз деп қарастыруға болады. Санау жүйесіндегі сандар цифрлар тізбегінен тұрады.
Санау жүйесі негізінен позициялы және позициясыз болып екіге бөлінеді. Егер цифрдың мағынасы оның тұрған орнына (яғни позициясына) тәуелсіз болса, ондай санау жүйесін позициясыз санау жүйесі деп аталады. Бұл жүйеге, мысал ретінде Рим санау жүйесін алуға болады. Рим санау жүйесінде ІХ (9), ХІІ (12) сандары тізбектің қай жерінде орналасса да, мағынасын (мәнін) өзгертпейді.
Егер цифрдың (яғни символдың) мағынасы оның тізбектегі орнына тәуелді болса, ондай санау жүйесі - позициялы санау жүйесі деп аталады. Мысалы, 222 санындағы цифрлардың түрлері ұқсас болғанымен, әрбіреуінің мағынасы әртүрлі, мұндағы оң жақта бірінші тұрған 2-бірлікті, оның алдындағы 2-жиырманы, ал үшінші орындағы 2 цифры - 200-ді білдіреді. Сондықтан олар бірліктер, ондықтар, жүздіктер деп аталады.

жүздік ондық бірлік
Санау жүйесінің алфавиті сол жүйесінің базисі деп аталады. Базис-жүйеге енетін цифрлардан (символдардан) құралады. Санау жүйесіне енетін базистер саны-жүйенің негізі деп аталады. Санау жүйесінің негізі ретінде үлкен оң натурал сан алынады да, ол көбінесе q әрпімен белгіленеді. q бірден үлкен кез келген сан болуы мүмкін, мысалы q=2, q=3, . . . , q=8, q=10, q=16. Мәселен, ондық санау жүйесіндегі 0, 1, 2, . . . , 9 цифрлары жүйенің базисі болып табылады, олардың саны 10, сондықтан бұл жүйенің негізі q=10. Екілік санау жүйесінде екі цифр 0 және 1 ғана бар, бұлар жүйенің базисі, мұнда q=2.
Кез келген санды былай жазуға болады:
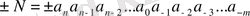 (1)
(1)
мұндағы,
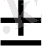 -санның таңбасы а-базиске енетін цифрлардың бірі, яғни q=10 болса, онда
-санның таңбасы а-базиске енетін цифрлардың бірі, яғни q=10 болса, онда
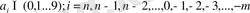
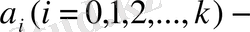 санның бүтін бөлшегі;
санның бүтін бөлшегі;
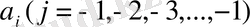 санның бөлшек бөлігі
санның бөлшек бөлігі
Мысалы, N=1989, 12 санын салайық, мұнда
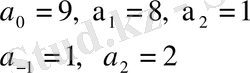
Кез келген позициялы санды жалпы түрде жазуға болады:
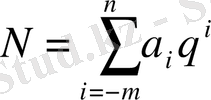 (2)
(2)
Мәселен

Сандар әр түрлі негізде жазылатын болғандықтан, олардың қандай жүйеге тиісті екендігін көрсету үшін оның негізін санның индексіне жазамыз: N(q)
Мысалы,
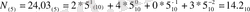
Күнделікті тұрмыста пайдаланып жүрген ондық санау жүйесі осы күнгі электрондық есептеуіш машиналар үшін жарамсыз.
Себебі, мұнда 10 цифр болғандықтан, ЭЕМ-нің зердесінде санның әрбір цифрын өрнектеу үшін оның ең болмағанда 10 тұрақты жағдайы болуы талап етіледі. Ондай машина жасау қиын және оның қажеті жоқ. Сондықтан компьютер үшін екілік негіздегі сандардан пайдалану ыңғайлы. Өйткені нөл санын физикалық мағынада желіде «импульс» жоқ, ал 1 санын «импульс» бар деп қарастыруға болады. ЭЕМ-де екілік жүйені пайдаланған кездің өзінде де схема 4 түрлі жағдайда беріледі.
Сандарды бір санау жүйесінен екінші санау жүйесіне көшіру жолдары бүтін сандар мен дұрыс бөлшектер үшін түрліше болады.
Бүтін сандарды көшіру
Берілген p санау жүйесінде Np санын q жүйесіне көшіру керек болсын. Ол үшін, егер p<q болса, онда q санының р жүйесіндегі мәнін табу керек, ал p>q болса онда q саны р жүйесіне енеді, сондықтан оны р жүйесіне көшірудің қажеті болмайды. Бұдан кейін берілген есепті шешуге кірісу керек.
 Ол үшін берілген Np санын q-ге бөліп, қалдықты анықтайды., бұл қалдық Np санын q жүйесінде көшіргенде шығатын санның ең кіші разрядындағы цифрды береді. Содан соң бөліндіні q санына тағы да бөліп, екінші қалдықты табады, бұл q негіздегі санның келесі қіші разрядындағы цифрды береді, т. с. с. Процесті осы тәртіппен соңғы бөлінді q-ден кіші болғанша жалғастырып, табылған қалдықтарды кері бағытта тізіп жазылса, q негізіндегі саны
Ол үшін берілген Np санын q-ге бөліп, қалдықты анықтайды., бұл қалдық Np санын q жүйесінде көшіргенде шығатын санның ең кіші разрядындағы цифрды береді. Содан соң бөліндіні q санына тағы да бөліп, екінші қалдықты табады, бұл q негіздегі санның келесі қіші разрядындағы цифрды береді, т. с. с. Процесті осы тәртіппен соңғы бөлінді q-ден кіші болғанша жалғастырып, табылған қалдықтарды кері бағытта тізіп жазылса, q негізіндегі саны
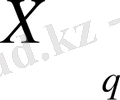 табылады. Np саны мен q саны p жүйесінде қарастырылатындықтан, бөлу де p жүйесінде жүргізіледі.
табылады. Np саны мен q саны p жүйесінде қарастырылатындықтан, бөлу де p жүйесінде жүргізіледі.
Мысалдар:
1. Ондық санау жүйесінде (p=10) берілген Np=857 санды сегіздік (q=8) жүйеде жазыңдар. 857 10 = x 8
Ереже бойынша бөлу былай орындалады:
857 8 Сонымен, х q =1531 8 болып шықты.
856 107 8
8 13 8
27 8
24
2. Сегіздік санау жүйесінде берілген N 8 =1726 8 санды ондық санау жүйесіне көшіріңдер. 1726 8 =x 10
Бұл есепті шығару үшін төмендегі екі жолдың бірін пайдалану керек:
1-жолы:
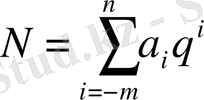 формуласы бойынша есептеу.
формуласы бойынша есептеу.
 яғни, 1726
8
=982
10
яғни, 1726
8
=982
10
2-жолы: Бүтін сандарды бір негізден екінші негізге көшіру әдісін көрейік. Бұл есепте p<q, яғни 8<10, олай болса ең алдымен q-ді р санау негізінде көшіру үшін жоғарыдағы ережені пайдалану керек, есептеулер р негізінде (яғни 8-дік жүйеде) жүргізілуі тиіс.
Яғни р=8, q=10.
- 8
- 8
ендеше 10 10 =12 8 10 10 =12 8
Ереже бойынша:
1726 12
-12 142 12
52 -12
- 50 22
26 - 12
- 24
11 8 , 10 8 , 2 8 - цифрлары 8-дік негіздегі цифрлар, олардың ондық жүйедегі мәндері мынадай:
11 8 =9 10 , 10 8 =8 10 ,
2 8 =2 10 , ендеше 1726 8 =982 10
Біздің негізгі мақсатымыз 10-дық негіздегі санды екілік негізге көшіру еді. Берілген мысалдарда 8-дік жүйеге көшкен себебіміз, егер берілген сан өте үлкен болса, оны 2-ге бөліп отыру көп уақыт алады және тиімсіз. Ал 8 саны 2 3 екені белгілі. Олай болса, әрбір 8- дік негіздегі цифрды оның жоғарыда көрсетілген үш орынды баламасымен алмастыру жеткілікті.
Мысалы,
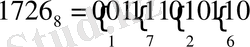 (2)
Демек 1726
8
= 010110
8
(2)
Демек 1726
8
= 010110
8
Бұл жағдайда санды бір негізден екінші негізге көшіруге қажетті операция саны үш есе азаяды.
3. 12 санын 2-лік санға айналдыру үшін:
- 2
12 6 2
0 6 3 2
0 2 1
1
Нәтижесі 1100 2 деген екілік сан болып шығады.
3. 12 санын 8-дік санға айналдыру үшін:
12 8
8 1
4
Нәтижесі 12
10
⇒ 14
8
саны шығады, ал 14
8
⇒ 1*8
 + 4*8
+ 4*8
 = 8+4=12
10
= 8+4=12
10
4. 65 санын 16-лық санға айналдыру үшін:
65 16
64 4
1
Нәтижесі 65
10
⇒ 41
16
саны шығады, ал 41
16
⇒ 4*16
 + 1*16
+ 1*16
 = 64+1=65
10
= 64+1=65
10
Санды сегіздік жүйеден бірденнен екілік жүйеге көшірудің мынадай қарапайым тәсілі қолдануға болады: әрбір сегіздік цифрды әрқайсысы үш екілік цифрдан тұратындай етіп екілік жүйеде өрнектейміз. Кері жағдайда, екілік санды оң жақтан бастап, әрқайсысын үш разрядтан топтарға ажыратып және бұл үштіктерді (триод) сегіздік түрінде жазамыз. Бұл топтардың әрқайсысында үш разряд толық болмаған жағдайда бос орындар нөлмен толықтырылады.
Мысалдар:
1 6 5
1. 165 8 ⇒ 001 111 101 ⇒ 1110101 2 (сол жақтағы нөлдер жазылмайды)
2 4
2. 10100 2 ⇒ 010 100 ⇒ 24 8
Екілік санды он алтылыққа көшіру үшін де ол санды оң жағынан бастап төрт разрядтан топтарға ажыратып және бұл төрттізбектерді (тетрады) он алтылық цифр түрінде жазуға болады. Керісінше, сегіздік санды екілікке көшіргендей, он алтылық санды да екілік санға көшіруге болады.
Мысалдар: G E F
- 11011102⇒ 0110 1110 ⇒ GEF16
2 7 4
2. 274 16 ⇒ 0010 0111 0100 ⇒ 1001110100 2
4. 12510 санын екілік негізге көшіріңдер 125 10 х 2
1-жол бойынша: 2-жол бойынша:
125 2
12 62 2 125 8
5 - 62 31 2 -8 15 8
-4 30 15 2 45 8 1
14 7 2 40 7
6 3 2 5
2
125 10 =175 8
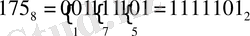
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz