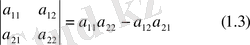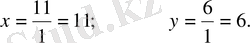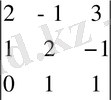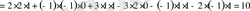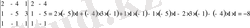Екінші және үшінші ретті анықтауыштар: Крамер формуласы, есептеу әдістері және қасиеттері


Екінші және үшінші ретті анықтауыштар.
 Екі белгісізі бар сызықтық екі теңдеу жүйесін қарастырайық
Екі белгісізі бар сызықтық екі теңдеу жүйесін қарастырайық
(1. 1)
Белгісіздерді анықтау үшін бірінші теңдеуді а
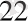 көбейтіп, ал екінші теңдеуді
көбейтіп, ал екінші теңдеуді
-
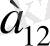 көбейтіп екі теңдеуді қосып белгісіз х-ті табамыз.
көбейтіп екі теңдеуді қосып белгісіз х-ті табамыз.
(
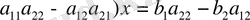
Осындай операцияны жасап белгісіз у-ті анықтаймыз:
(
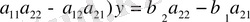
Соңғы екі теңдеулерден х және у айнымалыларды анықтаймыз:
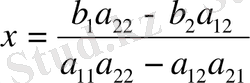
(1. 2)
(1. 2) формулаларда пайда болған
 ,
,
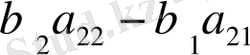 ,
,
 өрнектерді 2-ші ретті анықтауыштар деп атайды. Екінші ретті анықтауышты келесі символ (белгі) мен белгілейді:
өрнектерді 2-ші ретті анықтауыштар деп атайды. Екінші ретті анықтауышты келесі символ (белгі) мен белгілейді:
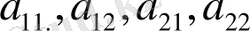 анықтауыштың элементтері.
анықтауыштың элементтері.
а
11
және а
22
бас диагональді құрайды, а
12
және
а
21
- қосымша диагональдың элементтері.
Егер анықтауыштарды :
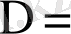
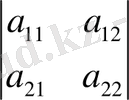
=
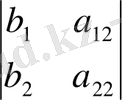
=
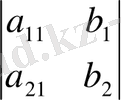
белгілесек онда (1. 2) формулалары келесі түрге келтіріледі:
х=
у=
(1. 4)
Айнымалылардың алдында тұрған коэффициентерінен құрылған
 анықтауышын жүйенің бас анықтауышы деп атайды. Ал
анықтауышын жүйенің бас анықтауышы деп атайды. Ал
 анықтауышы бас анықтауыштың бірінші бағандағы элементтерін жүйенің бос мүшелерімен алмастырылып құралады, ал
анықтауышы бас анықтауыштың бірінші бағандағы элементтерін жүйенің бос мүшелерімен алмастырылып құралады, ал
 - екінші бағанның элементтерін бос мүшелерден құралған бағанмен алмастырады.
- екінші бағанның элементтерін бос мүшелерден құралған бағанмен алмастырады.
(1. 4) формуларын Крамер формуласы деп атайды.
Мысал. Жүйені есептеңіз:
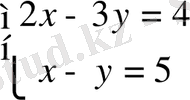
Шешімі: Бас анықтауышын есептейміз
 =
=
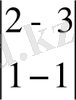 =2(-1) -(-3) 1= -2+3=1
=2(-1) -(-3) 1= -2+3=1
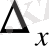 және
және
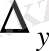 анықтауыштарын есептейміз:
анықтауыштарын есептейміз:
=
=4(-1) -5(-3) =11,
=
=10-4=6
(1. 4) формуласын қолданып, белгісіз х және у анықтаймыз:
Үшінші ретті анықтауыш келесі түрде жазылады:
a 11 , a 22 , a 33 элементтер бас диагоналін құрайды, ал а 13 а 22 а 32 элементтері қосымша диагоналін құрайды.
Үшінші ретті анықтауыштың і-ші жолындағы және j-ші бағанындағы элементтерін ойша сызғаннан қалған екінші ретті анықтауышты а ij элементінің миноры деп атайды. Осы элементтің минорын М ij арқылы белгілейді.
Мысалы: М
23
=
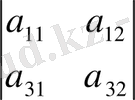 а
23
- элементтің миноры.
а
23
- элементтің миноры.
Алгебралық толықтауыш келесі формула арқылы анықталады:
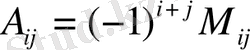
Мысалы: а 21 , а 33 элементтерінің алгебралық толықтауыштары
А
21
=(-1)
2+1
M
21
=(-1)
3
 = -
= -

A
33
=(-1)
3+3
M
33
=(-1)
6
 =
=
Үшінші ретті анықтауышты есептеу тәсілдері.
1) Үшбұрыш әдісі.

формуласымен анықталған санды үшінші ретті анықтауыш деп атайды.
Осы анықтауыштың мүшелерін табу үшін схемалық суретін келтірейік.
Осы схема бойынша есептелген анықтауыштың бірінші үш мүшесі өз таңбасымен алынады, ал келесі үш мүшесі теріс таңбалы болады.
Мысал. Анықтауышты есептеңдер:
Мүнда а 11 =2, а 12 =-1, а 13 =3, а 21 =1, а 22 =2, а 23 =-1, а 31 =0, а 32 =1, а 33 =1. Сонда (1. 5) формула бойынша
2) Сарриус әдісі. Үшінші ретті анықтауышқа оң жағына әуелі бірінші бағанды, содан екінші бағанды тіркеп жазамыз

- - + + +
Содан кейін тұтас сызықпен көрсетілген элементтерін көбейтіп өз ара қосамыз және өз таңбаларымен аламыз, ал үзік сызықтармен көрсетілген элементтерін көбейтіп өзара қосып теріс таңбамен аламыз. Содан кейін осыдан шыққан екі санды сәйкес таңбаларымен өзара қосып анықтауышты есептейміз.
Бүл ереже Сарриус ережесі деп аталады.
Мысал:
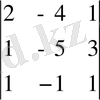 анықтауышты есептеңдер.
анықтауышты есептеңдер.
Сарриус әдісін қолданамыз:
3) . Анықтауышты жолы немесе баған элементтері арқылы жіктеп есептеу әдісі.
Анықтауыштың қандай болса да жолының (бағанның) элементтерін сәйкес алгебралық толықтауыштарына көбейтіп, қосқаннан шыққан қосынды анықтауыштың шамасына тең болады. Немесе
(бірінші жолы бойынша жіктеу) .
(бірінші баған бойынша жіктеу) .
Мысал: Бірінші жолдың элементтері арқылы жіктеп анықтауышты есептеңдер.
Анықтауыштың негізгі қасиеттері:
- Анықтауыштың жолдарын оның сәйкес бағандарымен орын алмастырғаннан ол анықтауыштың сан мәні өзгермейді.
- Егер анықтауыштың екі жолын (бағанын) бірімен-бірінің орындарын алмастырса онда анықтауыш таңбасы қарама-қарсы таңбаға ауысады.
- Егер анықтауыштың кез-келген екі жолы өзара тең болса, онда ол нөлге тең болады.
- Егер анықтауыштың қандай да болса бір жолының барлық элементтері нөлге тең болса, онда анықтауыш нөлге тең болады.
- Анықтауыштың жолының немесе бағанының элементтерінің ортақ көбейткішін анықтауыш алдына шығаруға болады.
- Егер анықтауыштың екі жолының элементтері өзара пропорционал болса онда анықтауыш нөлге тең.
- Анықтауыштың қандай да болса бір жолының элементтерін олардың сәйкес алгебралық толықтауыштарына көбейтіп қосқаннан шыққан қосынды анықтауыш шамасына тең болады.
- Егер анықтауыштың бір жолының элементтері екі қосылғыш арқылы берілген болса, онда анықтауыш екі анықтауыштың қосындысына тең болады. Бірінші анықтауыштың сәйкес жолында бірінші қосылғыш, екінші анықтауышта екінші қосылғыш.
- Егер анықтауыштың қандай болса да бір жолының элементтерін бір ғанасанына көбейтіп басқа бір жолының сәйкес элементтеріне қосса, онда бұдан анықтауыш шамасы өзгермейді.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz