Дискретті кездейсоқ шамалар: анықтамасы, бөлу заңдары және сандық сипаттамалары


Тақырыбы: Кездейсоқ шамалар
Мақсаты: кездейсоқ шама түсінігін, кездейсоқ шамаларды бөлу заңын енгізу, сонымен қатар, дискретті кездейсоқ шамалардың сандық сипаттамаларын қарастыру.
Жоспар:
- Кездейсоқ шаманың анықтамасы мен оның негізгі қасиеттері.
- Дискретті және үзіліссіз кездейсоқ шамалар.
- Дискретті кездейсоқ шаманы бөлу.
- Дискретті кездейсоқ шамалардың санық сипаттамалары:
- Математикалық күтім,
- мода,
- дисперсия,
- орташа квадраттық ауытқу.
- Дискретті кездейсоқ шамаларды үйлестірудің кейбір заңдары:
- Биноминальді үйлестіру,
- Пуассон үйлестіруі.
§ 1. Кездейсоқ шаманың анықтамасы мен оның қасиеттері.
Анықтама. Сынау нәтижесінде мүмкін мәндердің біреуін ғана қабылдайтын шамалар кездейсоқ шамалар деп аталады.
Анықтама. Шама кездейсоқ деп аталады, егер ол өз мәндерін сынау жағдайларына қаьтысты қабылдаса, сонымен қатар әр бір элементар оқиға үшін ол мән жалғыз болса.
§ 2. Дискретті және үзіліссіз кездейсоқ шамалар.
Кездейсоқ шамаларды дискретті және үзіліссіз деп бөлуге болады.
Анықтама. Кездейсоқ шама дискретті деп аталады, егер оның барлық мүмкін болатын мәндер жиыны ақырлы болса.
Анықтама. Дискреттік кездейсоқ шамалардың барлық мүмкін мәндері мен олардың ықтималдықтарының арасындағы сәйкестік кездейсоқ шаманың бөлу заңы деп аталады.
§ 3. Дискреттік кездейсоқ шамаларды бөлу заңы.
Дискреттік кездейсоқ шама Х берілді деп есептеледі, егер оның барлық мүмкін болатын мәндері мен ықтималдықтары берілсе.
Х - дискретті кездейсоқ шама болсын, оның мүмкін болатын мәндері: х 1 , х 2 , …, х n сандары болсын.
Р i = P(x = x i ) (i = 1, 2, …, n) арқылы асы мәндердің ықтималдығын белгілейік.
Слайд 1.
Анықтама: Дискреттік кездейсоқ шаманың барлық мүмкін болатын мәндері мен олардың ықтималдықтарының арасындағы сәйкестік берілген кездейсоқ шаманы бөлу заңы деп аталады.
Қарапайым жағдайда дискретті кездейсоқ шаманың мәндерінің бөлінуін кесте түрінде көрсеткен ыңғайлы:
х = х i (i = 1, …, n) оқиғалары оқиғалардың толық тобын құрайды, сондықтан да
p1 + p2+…+pn = 1.
Анықтама: Кездейсоқ шамалардың мәні мен олардың ықтималдықтары көрсетілген кестені сонымен қатар бөлу қатары деп атайды.
Слайд 2, 3.
Бөлу қатарын көрнекі түрде көрсету үшін оның графикалық бейнесі қолданылады: Ох осіне кездейсоқ шаманың мүмкін болатын мәндері, ал Оу осіне осы мәндердің ықтималдықтары бейнеленеді. Осындай фигураны бөлу көпбұрышы деп атайды.
§ 4. Дискретті кездейсоқ шамалардың сандық сипаттамалары.
Бөлу заңы дискреттік кездейсоқ шаманы толығымен сипаттайды. Алайда, кей жағдайларда ол белгісіз болады немесе оны сандар арқылы көрсету тиімдірек болады. Осы сандарды дискреттік кездейсоқ шаманың сандық сипаттамалары деп атаймыз. Олардың қатарына математикалық күтімді, дисперция мен орташа квадраттық ауытқуды жатқызуға болады.
Математикалық күтім.
Анықтама. Дискретті кездейсоқ шаманың математикалық күтімі деп оның барлық мүмкін болатын мәндері мен олардың ықтималдықтарының қосындысын айтамыз.
Слайд 4.
Кездейсоқ шаманың математикалық күтімі тұрақты шама, сондықтан да кездейсоқ шаманың сандық сипаттамасы болып табылады.
Математикалық күтім шамамен кездейсоқ шаманың орташа арифметикалық мәніне тең болады.
Слайд 5.
Математикалық күтімнің қасиеттері:
I. Тұрақты шаманың математикалық күтімі осы тұрақтының өзіне тең.
II . Екі немесе одан да көп кездейсоқ шаманың қосындысының математикалық күтімі осы шамалардың математикалық күтімінің қосындысына тең.
III . Екі немесе одан да көп кездейсоқ шамалардың көбейтіндісінің математикалық кұтімі осы шамалардың математикалық күтімінің көбейтіндісіне тең болады.
IV . Тұрақты көбейткішті математикалық күтім белгісінің сыртына шығаруға болады.
Мода
Математикалық күтімнен басқа кездейсоқ шаманың жағдайының сипаттамасы мода болып табылады.
Слайд 6.
Анықтама. Дискреттік бөлудің М 0 модасы деп кездейсоқ шаманың оның алдындағы және одан кейінгі мәндерінің ықтималдығы P(x m ) аспайтын қандай да бір х m санын айтамыз
Бір, екі немесе одан да көп модалары бар бөлулерді бірмодальді, екімодальді және көпмодальді деп атаймыз.
Дисперсия.
Анықтама. Дискретті кездейсоқ шаманың дисперциясы деп осы шаманың математикалық күтімінен ауытқуының квадратының математикалық күтімін айтамыз.
D(Х) = М{[X - М(Х) ]
 },
},
D(Х) =
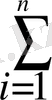 (Хi - М)
(Хi - М)
 ∙ Рi.
∙ Рi.
Слайд 7.
Дисперцияның қасиеттері:
I. Тұрақты санның дисперциясы 0-ге тең.
II. Тұрақты көбейткішті квадраттап дисперция белгісінің сыртына шығаруға болады .
III. Екі тәуелсіз кездейсоқ шамалардың дисперциясы осы екі шаманың дисперцияларының қосындысына тең.
Орташа квадраттық ауытқу.
Анықтама. Дисперциядан алынған квадрат түбір орташа квадраттық ауытқу деп аталады.
σ(Х) =

Слайд 8.
§ 5. Дискретті кездейсоқ шамаларды үйлестіруінің кейбір заңдары. Биноминальді үйлестіру
Слайд 9.
Анықтама. Мәндерінің ықтималдығы (p+q) n сәйкес мүшесіне тең дискреттік шаманың үйлестірілуі биномальді үйлестіру деп атаймыз. Р және n параметрлері толығымен биномарль үйлестіруді анықтайды.
P n (X) = C X n p X q n-X
Биномарлі үйлестіруге бағынатын кездейсоқ шаманың математикалық күтімі M(X) = np тең.
Биномарлі үйлестіруге бағынатын кездейсоқ шаманың дисперциясы D(X) = npq тең.
Биномарлы үйлестіруге бағынатын кездейсоқ шаманың орташа квадраттық ауытқуы σ = √npq тең.
Слайд 10.
Пуассона үйлестіруі.
Слайд 11.
Анықтама. Пуассон үйлестіруі деп келесі үйлестіруді айтамыз:
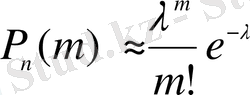 .
.
Көрнекілік материалдар (слайдтар) :
Слайд 1. Үйлестіру заңдары
Слайд 2. Үйлестіру көпбұрышы.
Слайд 3. Үйлестіру қатарын құру.
Слайд 4. Математикалық күтімді анықтау.
Слайд 5. Математикалық күтімнің анықтамасы.
Слайд 6. Мода.
Слайд 7. Дисперсия.
Слайд 8. Орташа квадраттық ауытқу.
Слайд 9. Биномарлі үйлестіру.
Слайд 10. Биномарлі үйлестіру мысалы.
Слайд 11. Пуассон үйлестіруі.
Слайд 1.
Үйлестіру заңдары
Кездейсоқ шаманың барлық мүмкін болатын мәндері.
Олардың ықтималдықтары.
Слайд 2.
Үйлестіру көпбұрышы.
Р i
P 3
P 4
P 2 P 5
0 P 1 P 6
x 1 x 2 x 3 x 4 x 5 x 6 X i
Слайд 3.
Үйлестіру қатарын құру.
Мысал:
Х үшін мүмкін болатын мәндер
Х1 = 1000 Х2 = 100 Х3 = 10 Х4 = 0
Олардың сәйкес ықтималдықтары
Р1 = 0, 0001; Р2 = 0, 001; Р3 = 0, 01; Р4 = 1- (Р1+Р2+Р3) = 0, 9889
Х үшін үйлестіру заңы:
Слайд 4.
Математикалық күтімді анықтау.
Егер x 1 , x 2 , …., x n дискретті кездейсоқ шаманың барлық мәндерінің жиыны, ал p 1 , p 2 , …, p n - оларға сәйкес ықтималдықтары болса, онда оның математикалық күтімі:
М(Х) = x
1
∙ p
1
+ x
2
∙ p
2
+…. + x
n
∙ p
n
=
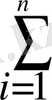 x
i
p
i
, где
x
i
p
i
, где
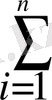 Рi = 1
Рi = 1
Мысал:
М(Х) = 1000 ∙ 0, 0001+100 ∙ 0, 001+10 ∙ 0, 01+ 0 ∙ 0, 9889=0, 3 тенге = 30 тиын.
Слайд 5.
Математикалық күтімнің қасиеттері.
I. М(С) = С.
II . М(Х ±Y) = М(Х) ± М(Y)
III . М(Х ∙ Y) = М(Х) ∙ М(Y),
IV . М(СХ) =СМ(Х)
Слайд 6.
Мода.
Слайд 7.
Дисперсия.
Анықтама.
D(Х) = М{[X - М(Х) ]
 },
},
D(Х) =
 (Хi - М)
(Хi - М)
 ∙ Рi.
∙ Рi.
Дисперция қасиеттері:
I. D(С) = 0
II.
D(СХ) = С
 D(Х) .
D(Х) .
III. D(Х ±Y) = D(Х) ± D(Y)
Слайд 8.
Орташа квадраттық ауытқу.
Есеп. Кездейсоқ шамалардың үйлестіру заңы келесі кесте арқылы берілсін:
М(Х) математикалық күтімін, D(Х) дисперциясы мен σ(Х) орташа квадраттық ауытқуын анықтау керек.
Шешуі :
М(Х) = 4 ∙ ¼ + 10 ∙ ½ + 20 ∙ ¼ = 11
D(Х) = (4 - 11)
 ∙ ¼ + (10 - 11)
∙ ¼ + (10 - 11)
 ∙ ½ + (20 - 11)
∙ ½ + (20 - 11)
 ∙ ¼ = 33
∙ ¼ = 33
σ(Х) =
 =
=
 ≈ 5, 75
≈ 5, 75
Слайд 9.
Биноминальді үйлестіру.
Анықтама.
P n (X) = C X n p X q n-X
P n (x)
0 1 2 3 4 . . . n x
M(X) = np. D(X) = npq. σ = √npq.
Слайд 10.
Биномальді үйлестірудің мысалдары.
Шешуі. p = 0. 7 q = 0. 3.
Кездейсоқ шама келесі мәндерді қабылдауы мүмкін 0, 1, 2, 3, 4, 5, 6.
Мүмкін болатын мәндердің ықтиалдығын Бернулли формуласы арқылы табамыз:
P 6 (0) = 0. 0007 P 6 (1) = 0. 01 P 6 (2) = 0. 057 P 6 (3) = 0. 18
P 6 (4) = 0. 32 P 6 (5) = 0. 3 P 6 (6) = 0. 11
Сәйкесінше биномарлы үйлестірудің ықтималдықтары келесі кесте арқылы беріледі:
Слайд 11.
Пуассон үйлестіруі.
Анықтама.

Шешуі: Бактериялар нүкте болып есептелетін суды араластыру жағдайында параметрі
μ = np = 10 000∙0. 001 = 10.
болатын Пуассон үйлестіруін қолдануға болады.
Бір тамшы суда бір де бір бактерия болмау ықтималдығын Пуассон заңы арқылы есептейміз:
P n (0) ≈ 0. 5∙10 -4 .
Бір тамшыда бір, екі немесе одан да көп бактериялардың болу ықтималдығы сәйкесінше:
P n (1) ≈ 5∙10 -4 ; P n (2) ≈ 25∙10 -4 ; P n (3) ≈ 83∙10 -4 ; …
Сәйкесінше үйлестіру заңы келесі кесте арқылы беріледі:
Әдебиеттер:
Негізгі:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz