Натурал сандар: жай және құрама сандар, кемелдік пен достастық қасиеттері және ЭЕМ көмегімен есептеу


Жамбыл атындағы облыстық №7 дарынды балаларға арналған мамандандырылған мектеп-интернаты
Натурал сандар жиыны
(мектепішілік ғылыми-практикалық конференцияға ұсынылады. )
Орындаған: 5-сынып оқушысы Айкеев Б
Жетекші: Мұстахаева В. М.
Қарағанды қаласы-2010ж.
«Кемел сан», «достас сан», «жай сан», «құрама сан», «жұп сан», «тақ сан» т. с. с. сан аталымдары ғылымға Пифагордың зерттеулері мен сабақтары арқылы біздің заманымыздан бұрынғы 6-5 ғасырлардан бері қарай кеңінен ене бастаған.
Ғылыми жұмыстың мақсаты: осы ұғымдарды жалпы зерттеу, бұл ұғымдармен қандай кемеңгер математиктер айналысты, қандай ерекше қасиеттері бар, қайда қолданылады, бір-бірімен қандай байланыста деген сұрақтарға жауап алу.
Ғылыми жұмыстың өзектілігі: 5-сыныптан біз жұп сан, тақ сан, жай және құрама сандармен таныспыз. Бірақ бұл сандардың арасындағы байланысты, достас сандарды, кемел сандарды біле бермейміз. Жұмыста осы мәселе қарастырылған. Ал қазіргі уақытта ЭЕМ қызметінде достас сандар, кемел сандар қолданылады.
Нәрселерді санауда қолданылатын сандар натурал сандар деп аталады. Біз мектеп математикасы курсынан натурал сандардың жұп және тақ, жай және құрама болып бөлінетіндігін білеміз. Ал «кемел сан», «достас сан» деген қандай сандар? Жай және құрама сандармен қандай байланыста? Бұл сұрақтарға жауап беру үшін санның бөлгіштері ұғымын, жай және құрама сандарды жақсы білу шарт. Санның бөлгіштері, 2-ге, 3-ке, 9-ға, 5-ке, 10-ға бөлінгіштік белгілері, құрама сандарды жай көбейткіштерге жіктеу, жұп және тақ сан ұғымдары бізге таныс болғанымен жұмыста қарастырдым.
Мектеп математикасы курсынан білетініміздей, жай сан дегеніміз тек 1 мен өзіне ғана бөлінетін натурал сан. Ал құрама сан деп бөлгіштерінің саны екеуден артық болатын натурал санды айтамыз.
Жай сандар жиынындағы есептерді шешу мәселелерімен Евклид, Эратосфен (1821-1894) ; академик Х. Гольдбах (1690-1764) ; академик И. М. Виноградов (1891-1983) сияқты кемеңгер математиктер кеңінен айналысып, ғылыми жемісті табыстарға жеткен.
Жұп және тақ сандар жай сандармен қандай байланыста? Бұл сұраққа жауапты келесі есептерден табамыз.
Гольдбах проблемасы . 5-тен үлкен кез-келген n натурал сан үш жай санның қосындысынан тұрады. Мысалы, 9= 2+2+5; 28=11+13+3; 85=79+3+3; т. с. с.
Эйлер проблемасы. 1) 2-ден артық кез-келген жұп сан екі жай санның қосындысынан тұрады. Мысалы, 4=2+2; 16=13+3; 84=79+5; т. с. с.
2) 5-тен артық кез-келген тақ сан үш жай санның қосындысынан тұрады. Мысалы, 7=2+2+3; 17=11+3+3; 85=79+3+3; т. с. с.
Пифагордың анықтамасы бойынша: кемел сан деп өзінің барлық мүмкін бөлгіштерінің қосындысына тең болатын санды айтады. Мысалы, 6, 28 сандарын кемел сандар деп айтуға болады. Өйткені 6 саны өзінің барлық бөлгіштерінің қосындысына тең 6=1+2+3. Сол сияқты 28= 1+2+4+7+14.
6 және 28 сандарының осындай ерекшелік қасиеттеріне әу бастан кемелдік немесе кереметтік мағына беріп қараушылар, көбінесе дүние жаратылымын діни оқу тұрғысынан түсіндірушілер болған. Олардың ойынша: «Бір алла бүкіл әлемді 6 күнде жаратқан», «Аспандағы Ай Жерді 28 тәулікте шарлап шығады». Сондықтан, 6 мен 28 сандары, көне де қасиеттері соларға ұқсас сандардың барлығы кемел сандар қатарына жатуы тиіс.
Математикалық тұрғыдан алғанда, кемел сандардың басты кереметі одардың жай сандармен тығыз байланыста болып келуінде. Ғылыми математиканың атасы Евклид (б. з. б. 330-275 жж. ) кемел сандарды есептеп табудың ережесін тапты.
Евклид теоремасы.
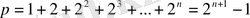 жай сан болса, онда
жай сан болса, онда
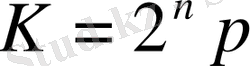 кемел сан болады.
кемел сан болады.
Евклид ережесі.
Егер де
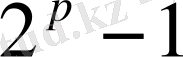 және
және
 - жай сан болса, онда мына қалыптама
- жай сан болса, онда мына қалыптама
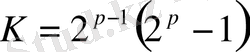 бүкіл жұп кемел сандар жиынын түгелдей өрнектейді.
бүкіл жұп кемел сандар жиынын түгелдей өрнектейді.
Осы Евклид ережесіне сүйене отырып,
 жай сандарға сәйкес келетін
жай сандарға сәйкес келетін
 кемел сандар тізбесін тауып көрейік.
кемел сандар тізбесін тауып көрейік.

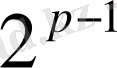
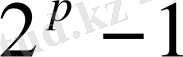
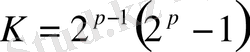
Евклид ережесіндегі
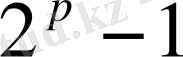 формуласы арқылы табылатын натурал сандар Марсенн сандары деп аталады. Бұл сандарды алғаш француз математигі Марен Марсенн (1588-1648) ашқан. Марсенн сандарына қатысты мынадай есеп қарастырдым:
формуласы арқылы табылатын натурал сандар Марсенн сандары деп аталады. Бұл сандарды алғаш француз математигі Марен Марсенн (1588-1648) ашқан. Марсенн сандарына қатысты мынадай есеп қарастырдым:
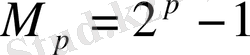 санының
санының
 құрмалас болғанда құрмалас, ал
құрмалас болғанда құрмалас, ал
 жай сан болғанда жай болатынын 1 мен 20 сандары арасында тексердім.
жай сан болғанда жай болатынын 1 мен 20 сандары арасында тексердім.
Қазіргі уақытта кемел сандарды электронды есептеуіш машиналардың көмегімен есептеп табуға болады.
Кемел сандар ұғымымен қатар Пифагор достас сандар ұғымын енгізіп, оны шәкірттері мен ізбасарларына кеңінен уағыздаған.
Егер А санының барлық бөлгіштерінің (өзінен басқа) қосындысы екінші В санына, ал В санының барлық мүмкін бөлгіштерінің (өзінен басқа) қосындысы А санына тең болса, онда А және В қос санды достас сандар деп атайды.
Мысалы, А= 284 саны үшін 1, 2, 4, 71, 142 сандары, ал В= 220 санына 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110 сандары бөлгіштер болады. Сонымен қатар мынадай теңдіктердің тура болатынына көз жеткізе аламыз 284=1+2+4+5+10+11+20+22+44+55+110; 220=1+2+4+71+142. Демек, (284, 220) қос сандары Пифагор анықтамасы бойынша достас сандар болып табылады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz