Жойылмалы эллиптік түрдегі теңдеулер үшін Дирихле есебінің спектрінің дискреттілігі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 53 бет
Таңдаулыға:
Мазмұны
Кіріспе . . . 5
1 Эллиптік түрдегі теңдеулер
1. 1 Лаплас теңдеуіне әкелетін есептер . . . 11
1. 2 Лаплас теңдеуін түрлендіру . . . 14
1. 3 Лаплас теңдеуінің кейбір дербес шешімдері . . . 17
1. 4 Гармоникалық функциялардың маңызды қасиеттері . . . 18
1. 5 Шеттік есептердің шешімін анықтау . . . 25
2 Функционалдық анализдің негізгі түсініктері мен кейбір фактілері
2. 1 Метрикалық кеңістік түсінігі . . . 32
2. 2 Сызықты және нормаланған кеңістіктер . . . 38
2. 3 Гильберт кеңістігі, ортогональдық . . . 40
2. 4 Сызықты операторлар теориясының элементтері . . . 42
2. 5 Кері операторлар . . . 44
3 Жойылмалы эллиптік түрдегі теңдеулер үшін Дирихле есебі спектрінің дискреттілігі
3. 1 Жойылмалы эллиптік түрдегі теңдеулер үшін Дирихле есебі спектрінің дискреттілігі . . . 46
Қорытынды . . . 53
Пайдаланылған әдебиеттер тізімі . . . 55
КІРІСПЕ
Тақырыптың өзектілігі. Эллиптiк түрдегі теңдеулер стационарлық (тұрақты) процестердi, мысалы, денеде тұрақты температураның таралуы, өткiзгiштiң бетiндегi электр зарядтарының тепе-теңдiк күйi, сұйықтың потенциалды ағысы т. с. с. процестердi сипаттайды.
Эллиптiк түрдегі теңдеулер үшiн қойылған шеттiк есептердiң шешiмiн табу үшiн әртүрлi әдiстер қолданылады. Олардың iшiнде жиi қолданылатыны Фурье әдiсi, Грин функциясы әдiсi, интегралдық теңдеулер әдiсi т. б.
Дифференциалды теңдеулерді зерттеуде қойылатын негізгі сұрақтарды үш топқа біріктіруге болады: шешімнің бар болуы, жалғыздығы және сапалық өзгерістері. Бұл сұрақтардың алғашқы екеуі теңдеудің математикалық моделі ретінде белгілі бір процесті сипаттайтынына жауап берсе, ал үшіншісі процестің өзгеруін сипаттайды. Сондықтан сызықты және сызықты емес дифференциалды теңдеулер теориясында үшінші мәселе, яғни теңдеу шешімнің сапалық өзгерістерін зерттеу үлкен орын алады. Соның ішінде бізді төмендегідей сұрақтар қызықтырады: 1) шешімнің тегістігі 2) шешімнің әр түрлі салмақты нормалардағы бағасы 3) шешімнің аппроксимативті қасиеттері.
Эллиптік түрдегі операторларға қарағанда, жойылмалы эллиптік түрдегі операторлардың спектральды сұрақтары аз зерттелген. Бұл бағыттағы немесе осыған жақын жұмыстар М. М. Смирновтың, Х. Трибелдің, М. В. Келдыштың, П. Боллей және Т. Камюдің, О. А. Олейниктің, М. Отелбаевтың, Т. Ш. Кальменовтың, М. Б. Муратбековтың, Л. К. Кусаинова мен М. С. Айтенованың және басқа да ғалымдардың еңбектерінде кездеседі.
Бірақта, бұл еңбектерде асимптотикалық бағыты және меншікті мәндері сияқты дәстүрлі сұрақтар зерттелмеген.
Жұмыс мақсаты. Жұмыстың негізгі мақсаты жойылмалы эллиптік түрдегі теңдеулер үшін Дирихле есебі спектрінің дискреттілігі.
Зерттеу әдістемесі. жойылмалы эллиптік түрдегі теңдеулер үшін Дирихле есебі спектрінің дискреттілігін зерттеу барысында төмендегідей әдістер пайдаланылды: априорлы бағалау әдісі және М. Б. Мұратбеков пен М. Өтелбаевтың жұмыстарында ұсынылған әдістер қолданылды.
Ғылыми жаңашылдығы. Жұмыста төмендегідей жаңа нәтижелер алынды:
- сызықты екінші ретті жойылмалы эллиптік түрдегі теңдеулер үшін Дирихле есебі спектрінің дискреттілігі алынды.
- Қарастырылған оператордың өз-өзіне түйіндес емес болған жағдайдағы синулярлы сандары (s-сандары) .
Практикалық және теориялық құндылығы. Кванттық механикада, беттердің ақырсыз аз иілу теориясында дифференциялды операторлардың спектральді теориясында сондай-ақ, жоғары курс студенттеріне арнайы курс оқу барысында қолданылатын теориялық қызығушылық тудыратын нәтижелер алынды.
Жұмыстың апробациясы . Қарастырылып отырған диссертациялық жұмыс нәтижелері Тараз мемлекеттік педагогикалық институты хабаршысы, ғылыми педагогикалық журналында (2011, №6) «О существовани периодических решений нелинейных вырождающихся уравнений» тақырыбында және 2011 жылы желтоқсанда Таразда болған «ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ ИНТЕГРАЦИЯСЫ: ПРОБЛЕМАЛАРЫ МЕН БОЛАШАҒЫ» атты Республикалық ғылыми-практикалық конференциясында «Жойылмалы эллиптік түрдегі теңдеулердің бір класы үшін шешімнің бар болуы» тақырыптарында жарық көрді.
Диссертация құрылымы. Жұмыс кіріспе, үш бөлім, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспеде тақырыптың өзектілігі негізделген, негізгі мақсаттары келтірілген, жұмыстың жаңалығы мен теориялық және практикалық маңыздылығы анықталған.
Бірінші бөлімде әдебиетке шолу жасалып, эллиптік түрдегі теңдеулердің кластарға бөлінуі, айнымалыны ажырату әдістері көрсетіліп мысалдармен ұштастырылған.
Екінші бөлімде функционалдық анализдің кейбір фактілері мен тұжырымдары және көмекші нәтижелер келтірілген.
Үшінші бөлімде жойылмалы эллиптік түрдегі теңдеулер үшін Дирихле есебі спектрінің дискреттілігі шарттары көрсетілген.
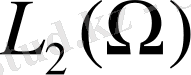 кеңістігінде төмендегі дифференциалдық операторды қарастырайық,
кеңістігінде төмендегі дифференциалдық операторды қарастырайық,
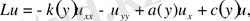 (1)
(1)
мұндағы Ω={(x, y) : -π< x<π, 0<y<1} тіктөртбұрыш.
(1) операторы
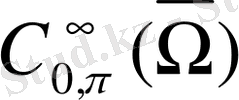 -
-
 облысындағы
у
айнымалысы бойынша барлық ретті дифференциалдары анықталған функциялар жиынында берілсін және
облысындағы
у
айнымалысы бойынша барлық ретті дифференциалдары анықталған функциялар жиынында берілсін және
 (2)
(2)
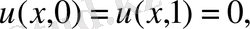 (3)
(3)
шарттарын қанағтаттандырсын.
L операторының коэффициенттері төмендегі шарттарды қанағаттандырсын деп ұйғарайық:
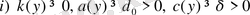 - функциялары [0, 1] кесіндісінде бөлікті үзіліссіз;
- функциялары [0, 1] кесіндісінде бөлікті үзіліссіз;
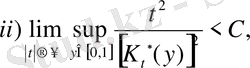 мұндағы С>0 - кейбір бағаланған сан және
мұндағы С>0 - кейбір бағаланған сан және
 теңдеуімен анықталған функция:
теңдеуімен анықталған функция:
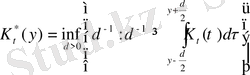 ,
,
мұндағы
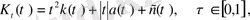 -∞<t<∞.
-∞<t<∞.
Теорема 1.
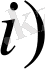 шарты орындалсын деп ұйғарайық. Онда L операторының
шарты орындалсын деп ұйғарайық. Онда L операторының
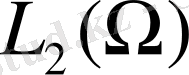 кеңістігінде үзіліссіз кері операторы бар.
кеңістігінде үзіліссіз кері операторы бар.
Теорема 2.
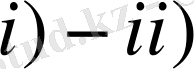 шарттары орындалсын. Онда
шарттары орындалсын. Онда
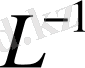 кері операторының
кері операторының
 сандары үшін төмендегі теңсіздік орынды
сандары үшін төмендегі теңсіздік орынды
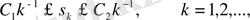
мұндағы С 1 және С 2 сандары тұрақты сандар, яғни 0< С 1 ≤ С 2 .
Анықтама 1.
Егер
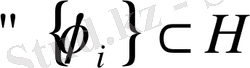 үшін
үшін
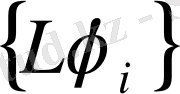 тізбегінің құрамында жинақты ішкі тізбек бар болса онда
тізбегінің құрамында жинақты ішкі тізбек бар болса онда
 операторы жете үзіліссіз деп аталады.
операторы жете үзіліссіз деп аталады.
Анықтама 2.
Егер
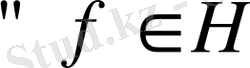 функциясы үшін
функциясы үшін
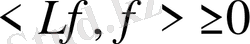 шарты орындалса, онда сызықты шенелген
шарты орындалса, онда сызықты шенелген
 операторы теріс емес деп аталады, және
операторы теріс емес деп аталады, және
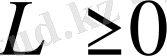 белгіленеді.
белгіленеді.
Айталық
 кез келген шенелген оператор болсын, онда
кез келген шенелген оператор болсын, онда
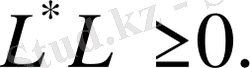 Себебі:
Себебі:
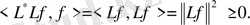
Жете үзіліссіз сызықты кез келген
 операторы үшін
операторы үшін
 операторын төмендегідей анықтаймыз:
операторын төмендегідей анықтаймыз:
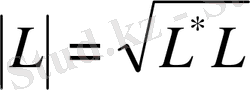 .
.
Анықтама 3.
 операторының меншікті мәндері
операторының меншікті мәндері
 операторының
операторының
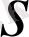 -сандары (Шмид бойынша меншікті мәндері) деп аталады.
-сандары (Шмид бойынша меншікті мәндері) деп аталады.
Нөлден өзгеше
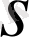 -сандарының еселіктерін ескеріп кему ретімен нөмірлейміз, яғни
-сандарының еселіктерін ескеріп кему ретімен нөмірлейміз, яғни
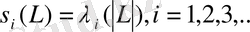 .
.
Мұндағы
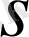 -сандары оң және нақты сандар.
-сандары оң және нақты сандар.
Анықтама 4.
Егер
 компактілі операторы
компактілі операторы
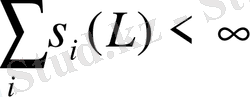
шартты қанағаттандырса, онда
 операторы ядролы оператор деп аталады.
операторы ядролы оператор деп аталады.
Айталық
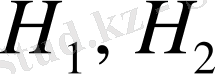 -банах кеңістіктері
-банах кеңістіктері
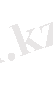
 кеңістігі
кеңістігі
 кеңістігіне енгізілген және
кеңістігіне енгізілген және
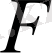 жиыны
жиыны
 кеңістігіндегі бірлік шар болсын.
кеңістігіндегі бірлік шар болсын.
Анықтама 5.
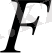 жиыны
жиыны
 кеңістігінің метрикасында мүмкін болатын өлшемі
кеңістігінің метрикасында мүмкін болатын өлшемі
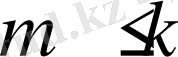
 сызықты көпбейнелерінен ауытқуларының төменгі шені
сызықты көпбейнелерінен ауытқуларының төменгі шені
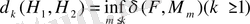
 -дің
-дің
 -ге енуінің Колмогоров көлденеңдері деп аталады, яғни анықтама бойынша
-ге енуінің Колмогоров көлденеңдері деп аталады, яғни анықтама бойынша
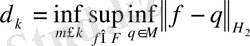
мұндағы
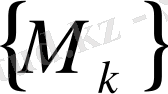 мүмкін болатын сызықты көпбейнелер жиынтығы.
мүмкін болатын сызықты көпбейнелер жиынтығы.
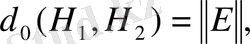 мұндағы
мұндағы
 енгізу оераторы.
енгізу оераторы.
Тікелей анықтамадан шығатын көлденеңдердің мынандай қасиеттері бар:
1.
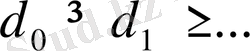
2.
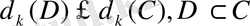
3.
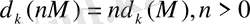 мұндағы
мұндағы
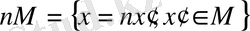
Колмогоров көлденеңдерінің екінші анықтамасы іспеттес келесі теорема орынды болады.
Теорема.
Айталық
 қандай да бір жете үзіліссіз оператор, онда
қандай да бір жете үзіліссіз оператор, онда
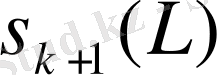 саны
саны
 жиынының
жиынының
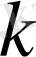 -шы Колмогоров көлденеңімен сәйкес келеді, яғни
-шы Колмогоров көлденеңімен сәйкес келеді, яғни
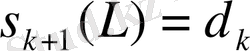 .
.
Мұндағы
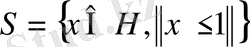 бірлік шар.
бірлік шар.
Колмогоров көлденеңдерінің бұл келтірілген анықтамасы көптеген жағдайларда біріншіге қарағанда ұтымды болады.
Келесі функцияны енгізейік:
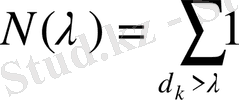
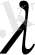 -дан үлкен көлденеңдердің саны.
-дан үлкен көлденеңдердің саны.
Бұл функция көлденеңдерді тарату функциясы немесе санаушы функция деп аталады.
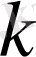 -шы көлденеңдермен оларды тарату функциясының арасында мынандай байланыс бар
-шы көлденеңдермен оларды тарату функциясының арасында мынандай байланыс бар
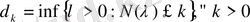 .
.
Соңғы теңдік көлденеңдерді бағалау үшін олардың тарату функцияларын бағалауға болатынын білдіреді.
Лемма 1.
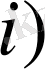 шарты орындалсын. Онда:
шарты орындалсын. Онда:
а) барлық
 үшін төмендегі теңсіздік орынды
үшін төмендегі теңсіздік орынды
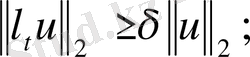
б)
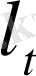 операторының үзіліссіз кері операторы бар.
операторының үзіліссіз кері операторы бар.
Лемма 2.
.
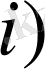 шарты орындалсын. Онда барлық
шарты орындалсын. Онда барлық
 үшін төмендегі баға орынды
үшін төмендегі баға орынды
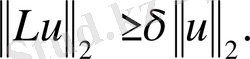
Лемма 3.
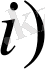 шарты орындалсын. Онда барлық
шарты орындалсын. Онда барлық
 төмендегі баға орынды:
төмендегі баға орынды:
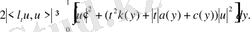
Лемма 4.
 шарттары орындалсын. Онда кез келген
шарттары орындалсын. Онда кез келген
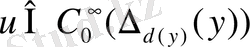 үшін
үшін
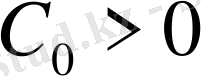 тұрақтысы табылып, мұндағы
тұрақтысы табылып, мұндағы
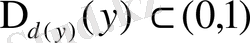 төмендегі теңсіздік орынды
төмендегі теңсіздік орынды
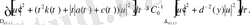
Лемма 5.
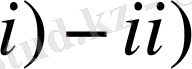 шарттары орындалсын. Онда төмендегі
шарттары орындалсын. Онда төмендегі
баға орынды
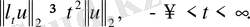
Лемма 6.
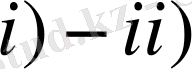 шарттары орындалсын. Онда барлық
шарттары орындалсын. Онда барлық
 үшін төмендегі баға орынды:
үшін төмендегі баға орынды:
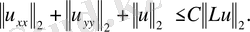
мұндағы С>0-тұрақты сан.
1 Эллиптiк түрдегі теңдеулер
1. 1 Лаплас теңдеуіне келтірілетін есептер
Эллиптiк түрдегі теңдеулер стационарлық (тұрақты) процестердi, мысалы, денеде тұрақты температураның таралуы, өткiзгiштiң бетiндегi электр зарядтарының тепе-теңдiк күйi, сұйықтың потенциалды ағысы т. с. с. процестердi сипаттайды. Осы сияқты процестердi зерттеулер Лаплас теңдеуiнiң шешiмiн табу амалына әкеледi. Лаплас теңдеуi
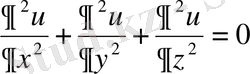 (1. 1. 1)
(1. 1. 1)
түрiнде жазылады.
Теңдеудiң сол жағына
 Лаплас операторын қолданып былай жазуға болады.
Лаплас операторын қолданып былай жазуға болады.
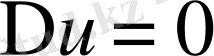
Екi тәуелсiз айнымалылар үшiн Лаплас теңдеуi
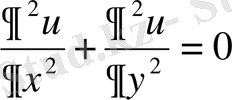
түрiнде, жазылады. Ал
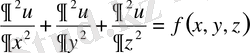
түрiндегi теңдеу Пуассон теңдеуi деп аталады.
Лаплас теңдеуiн қанағаттандыратын u функциялары гармоникалық функциялар деп аталады.
Бiртектi денеде температураның тұрақталып таралуы
Бiртектi
Т
денесi
 бетiмен шектелген болсын дейiк. Дененiң әртүрлi нүктелерiндегi температура
бетiмен шектелген болсын дейiк. Дененiң әртүрлi нүктелерiндегi температура
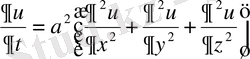
теңдеуiн қанағаттандырады. Егер температура уақыттан тәуелсiз болса, яғни
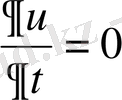 , онда дененiң температурасы Лаплас теңдеуiн қанағаттандырады.
, онда дененiң температурасы Лаплас теңдеуiн қанағаттандырады.
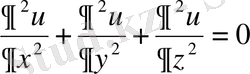
Осы теңдеуден дененiң температурасы бiр мәндi анықталуы үшiн
 бетiндегi температураны бiлу керек. Сондықтан (1. 1. 1) теңдеу үшiн шеттiк есеп былай қойылады:
бетiндегi температураны бiлу керек. Сондықтан (1. 1. 1) теңдеу үшiн шеттiк есеп былай қойылады:
1 0 Дирихле есебi (бiрiншi шеттiк есеп)
Берiлген
Т
облысында гармоникалық функция болатын, тұйық
 облысында үзiлiссiз және облыстың
облысында үзiлiссiз және облыстың
 шекарасында берiлген үзiлiссiз
шекарасында берiлген үзiлiссiз
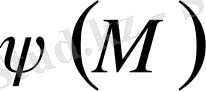 функциясына тең, яғни
функциясына тең, яғни
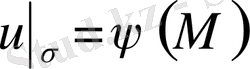 (1. 1. 2)
(1. 1. 2)
шартын қанағаттандыратын
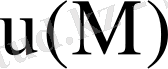 функциясын табу керек. Егер температураның таралуы жазықтықтағы
С
контуры мен
D
облысында қарастырылатын болса, онда
функциясын табу керек. Егер температураның таралуы жазықтықтағы
С
контуры мен
D
облысында қарастырылатын болса, онда
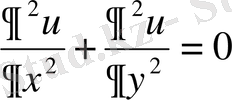
теңдеуiн қанағаттандыратын және
С
контурында
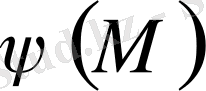 функциясына тең
u(x, y)
функциясын табу керек.
функциясына тең
u(x, y)
функциясын табу керек.
2 0 Нейман есебi (екiншi шеттiк есеп)
Берiлген
Т
облысында гармоникалық функция болатын, тұйық
 облысында үздiксiз дифференциалданатын, ал
облысында үздiксiз дифференциалданатын, ал
 тегiс бетiнен сыртқа қарай бағытталған нормаль бойынша алынған
тегiс бетiнен сыртқа қарай бағытталған нормаль бойынша алынған
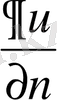 туындысы осы беттiң нүктелерiнде берiлген
туындысы осы беттiң нүктелерiнде берiлген
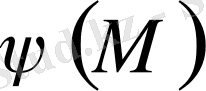 үздiксiз функциясына тең болатын, яғни
үздiксiз функциясына тең болатын, яғни
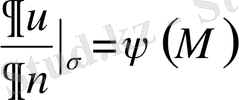 (1. 1. 3)
(1. 1. 3)
шартын қанағаттандыратын u(M) функциясын табу керек.
3 0 Аралас есеп (үшiншi шеттiк есеп)
Берiлген
Т
облысында гармоникалық болатын,
 тұйық облысында үздiксiз дифференциалданатын, ал сол
u(M)
функциясының және оның нормальдiк бағыт бойынша алынған
тұйық облысында үздiксiз дифференциалданатын, ал сол
u(M)
функциясының және оның нормальдiк бағыт бойынша алынған
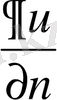 туындысының сызықтық комбинациясы
туындысының сызықтық комбинациясы
 тегiс бетiнде берiлген үздiксiз функциясына тең болатын, яғни
тегiс бетiнде берiлген үздiксiз функциясына тең болатын, яғни
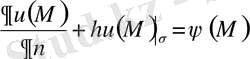 (1. 1. 4)
(1. 1. 4)
шартын қанағаттандыратын u(M) функциясын табу керек.
Егер есептiң шешiмiн
 бетiмен қоршалған iшкi облыста немесе одан сырт облыста табу керек болса, онда есеп тиiсiнше iшкi немесе сыртқы шеттiк есеп деп аталады.
бетiмен қоршалған iшкi облыста немесе одан сырт облыста табу керек болса, онда есеп тиiсiнше iшкi немесе сыртқы шеттiк есеп деп аталады.
Сұйықтың потенциалды ағыны
Екiншi мысал ретiнде сұйық ағынының көзi жоқ, яғни сығымдалмайтын сұйықтың потенциалды ағынын қарастырайық. Шекарасы
 болатын қандай да бiр
Т
облысының iшiнде
v(x, y, z)
жылдамдықпен сипатталатын сығымдалмайтын сұйықтың (тығыздығы
болатын қандай да бiр
Т
облысының iшiнде
v(x, y, z)
жылдамдықпен сипатталатын сығымдалмайтын сұйықтың (тығыздығы
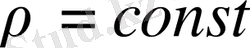 ) стационар ағыны бар болсын дейiк. Егер сұйық ағыны құйынсыз болса, онда
) стационар ағыны бар болсын дейiк. Егер сұйық ағыны құйынсыз болса, онда
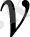 жылдамдығы потенциалдық вектор болады, яғни
жылдамдығы потенциалдық вектор болады, яғни
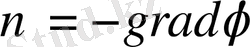 (1. 1. 5)
(1. 1. 5)
Мұндағы
 - жылдамдық потенциалы деп аталатын скалярлық функция. Егер ағын көздерi жоқ болса, онда
- жылдамдық потенциалы деп аталатын скалярлық функция. Егер ағын көздерi жоқ болса, онда
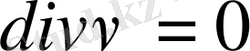
Осыны (1. 1. 5) теңдеуге қойып,

немесе
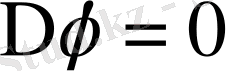
теңдеуiн аламыз. Осыдан потенциалдық жылдамдық Лаплас теңдеуiн қанағаттандыратынын көремiз.
1. 2 Лаплас теңдеуiн түрлендiру
Алдымен екi өлшемдi және үш өлшемдi кеңiстiктердегi негiзгi координаталар жүйелерiн еске салайық:
Екi өлшемдi кеңiстiктегi тiк бұрышты декарт координаталар жүйесi;
Үш өлшемдi кеңiстiктегi тiк бұрышты декарт координаталар жүйесi;
Екi өлшемдi кеңiстiктегi полярлық координаталар;
Үш өлшемдi кеңiстiктегi цилиндрлiк координаталар;
Үш өлшемдi кеңiстiктегi сфералық координаталар;
Полярлық координаталар мынадай арақатынастармен анықталады.
а)
y
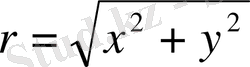 ,
,
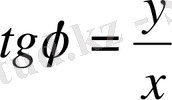 ,
,
немесе,
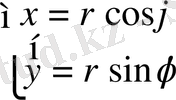
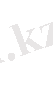
Цилиндрлік координаталаp
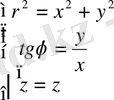 немесе
немесе
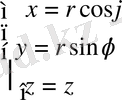
Сфералық координаталар
в)
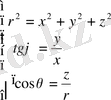 немесе
немесе
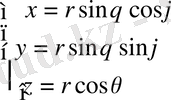
1-сурет
Лаплас теңдеуiнде полярлық координаталарға көшейiк:
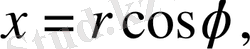
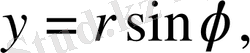
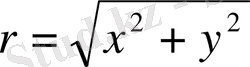 ,
,
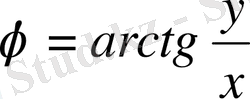 егер
x>0
болса,
егер
x>0
болса,
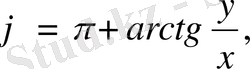 егер x<0,
егер x<0,
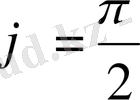 , егер x=0, y>0,
, егер x=0, y>0,
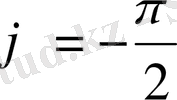 егер
x=0, y<0
егер
x=0, y<0
болғандықтан, мынадай түрлендiрулер жүргiземiз:
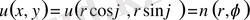
және
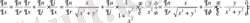
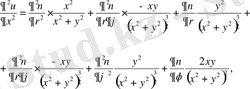
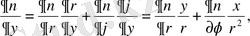

Осыларды теңдеуге қоямыз
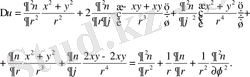
Сонымен
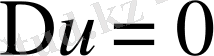 Лаплас теңдеуi полярлық координаталармен былай жазылады
Лаплас теңдеуi полярлық координаталармен былай жазылады
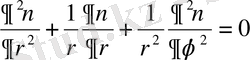 (1. 2. 1)
(1. 2. 1)
Лаплас теңдеуiнiң цилиндрлiк координаталармен берiлген түрi.
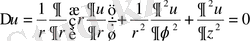 (1. 2. 2)
(1. 2. 2)
Лаплас теңдеуiнiң сфералық координаталармен берiлген түрi
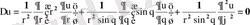 (1. 2. 3)
(1. 2. 3)
1. 3 Лаплас теңдеуiнiң кейбiр дербес шешiмдерi
Сфералық симметриялы
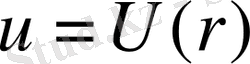 Лаплас теңдеуiнiң шешiмi
Лаплас теңдеуiнiң шешiмi
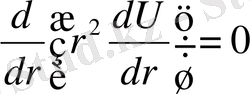
жай дифференциалдық теңдеуiнен анықталады. Бұл теңдеудi интегралдап,
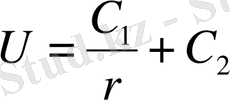
шешiмiн аламыз. Мұндағы С 1 және С 2 - кез-келген тұрақтылар. Егер С 1 =1, С 2 =0 деп алатын болсақ, онда Лаплас теңдеуiнiң кеңiстiктегi
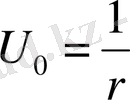 (1. 3. 1)
(1. 3. 1)
фундаменталды шешiмiн аламыз.
Осы сияқты
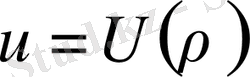 деп алып және (1. 2. 1) не (1. 2. 2) теңдеулердi пайдаланып, цилиндрлiк немесе дөңгелектi симметриялы болатын шешiм аламыз:
деп алып және (1. 2. 1) не (1. 2. 2) теңдеулердi пайдаланып, цилиндрлiк немесе дөңгелектi симметриялы болатын шешiм аламыз:
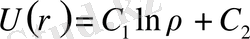
Егер С 1 =-1, С 2 =0 деп алатын болсақ, онда
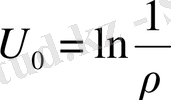 (1. 3. 2)
(1. 3. 2)
теңдiгiн аламыз. Бұл функцияны жазықтықтағы Лаплас теңдеуiнiң фундаменталды шешiмi деп атайды.
1. 4 Гармоникалық функциялардың маңызды қасиеттерi
Гармоникалық функциялардың қасиеттерiн қарастырғанда Гриннiң формулалары жиi қолданылады.
Гриннiң бiрiншi формуласы
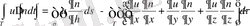 (1. 4. 1)
(1. 4. 1)
Гриннiң екiншi формуласы
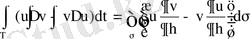 (1. 4. 2)
(1. 4. 2)
Осы формулаларды дәлелдейiк.
Остроградский - Гаусс формуласын жазайық
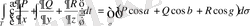 (1. 4. 3)
(1. 4. 3)
мұндағы - көлем элементтерi
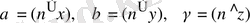 -
-
 бетiнен жүргiзiлген сыртқы нормальдардың координата осьтерiмен жасайтын бұрыштары.
бетiнен жүргiзiлген сыртқы нормальдардың координата осьтерiмен жасайтын бұрыштары.
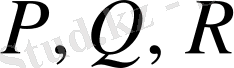 - кез-келген дифференциалданатын функциялар. Егер
- кез-келген дифференциалданатын функциялар. Егер
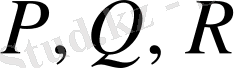 функцияларын
функцияларын
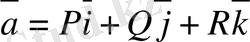 векторының компоненттерi ретiнде қарастыратын болсақ, онда (1. 4. 3) формулаларын былай жазуға болады.
векторының компоненттерi ретiнде қарастыратын болсақ, онда (1. 4. 3) формулаларын былай жазуға болады.
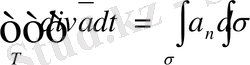 (1. 4. 3
/
)
(1. 4. 3
/
)
Мұнда -
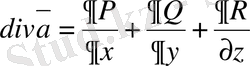 және
және
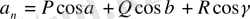 . Ендi
. Ендi
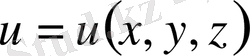 және
және
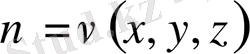 - өздерiнiң бiрiншi туындыларымен бiрге
- өздерiнiң бiрiншi туындыларымен бiрге
 облысының iшкi жағында үзiлiссiз функция ал
Т
облысының iшкi жағында үзiлiссiз екiншi туындылары бар болсын. Әрi қарай
облысының iшкi жағында үзiлiссiз функция ал
Т
облысының iшкi жағында үзiлiссiз екiншi туындылары бар болсын. Әрi қарай
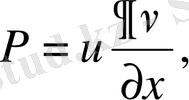
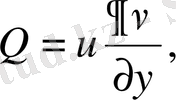
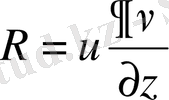
деп алып, (1. 4. 3 / ) Остроградский - Гаусс формуласын пайдаланып Гриннiң бiрiншi формуласын (1. 4. 1) аламыз.
Мұндағы
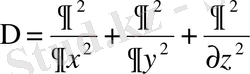 - Лаплас операторы,
- Лаплас операторы,
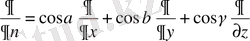 - сыртқы нормаль бағыты бойынша алынған туынды.
- сыртқы нормаль бағыты бойынша алынған туынды.
Егер
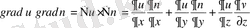 . 3
. 3
арақатынасын ескерсек, онда Грин формуласын былай жазуға болады:
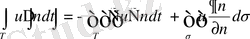 (1. 4. 1
/
)
(1. 4. 1
/
)
Осындағы
 мен
мен
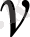 - лардың орнын ауыстырып жазайық:
- лардың орнын ауыстырып жазайық:
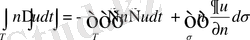
Осы теңдiктi (1. 4. 1 / ) теңдiктен алып тастап, Гриннiң екiншi формуласын аламыз:
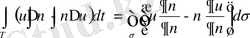 (1. 4. 2
/
)
(1. 4. 2
/
)
Ендi гармоникалық функциялардың қасиеттерiне тоқталайық.
1 0 Тегiс тұйық S бетi D ашық облысында жататын болсын және f осы D облысындағы гармоникалық функция. Онда
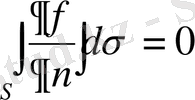 (1. 4. 4)
(1. 4. 4)
Мұндағы
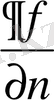 -
тегiс
S
бетiне нормаль бағыты бойынша алынған
f
функциясының туындысы. Ал
-
тегiс
S
бетiне нормаль бағыты бойынша алынған
f
функциясының туындысы. Ал
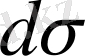 -
бет ауданының элементi.
-
бет ауданының элементi.
2 0 Ашық D облысында f гармоникалық функция болсын. Онда
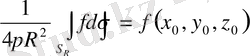 (1. 4. 5)
(1. 4. 5)
Мұндағы
S
R
- D
облысындағы центрi
(x
0
, y
0
, z
0
)
нүктесiнде жататын және радиусы R-ға тең сфера, ал
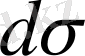 - сфера бетiнiң аудан элементi.
Бұл
2
0
қасиет D облысындағы кез-келген сфераның бетiндегi f функциясының орта мәнi сфераның центрiндегi функцияның мәнiне тең екендiгiн көрсетедi.
- сфера бетiнiң аудан элементi.
Бұл
2
0
қасиет D облысындағы кез-келген сфераның бетiндегi f функциясының орта мәнi сфераның центрiндегi функцияның мәнiне тең екендiгiн көрсетедi.
3 0 Максимум принципi. Шекарасы S болатын D тұйық облысында f гармоникалық функция болса, онда f функциясының кез-келген жекеленген экстремумы шекаралық нүктелерде қабылданады.
4
0
Шекарасы S болатын
D
тұйық облысында
u
және
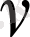 гармоникалық функциялар болып және
S
бетiнде
u
>
гармоникалық функциялар болып және
S
бетiнде
u
>
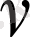 теңсiздiгi орындалса, онда D - ның барлық нүктелерiнде u
теңсiздiгi орындалса, онда D - ның барлық нүктелерiнде u
 шарты орындалады.
шарты орындалады.
5
0
Комплекс айнымалысының
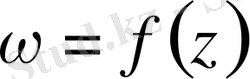 функциясы z=x+yi нүктесiнде аналитикалық функция болсын. Онда
функциясы z=x+yi нүктесiнде аналитикалық функция болсын. Онда
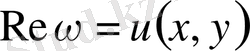 және
және
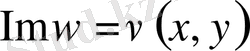 функциялары
(x, y)
нүктесiнiң маңайында гармоникалық функциялар болады.
функциялары
(x, y)
нүктесiнiң маңайында гармоникалық функциялар болады.
Дәлелдеу.
1
0
S
бетiмен шектелген
D
облысындағы тегiс
 векторлық өрiсi үшiн Остроградский формуласы орындалады:
векторлық өрiсi үшiн Остроградский формуласы орындалады:
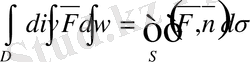
Мұндағы
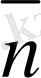 - S бетiне сыртқы нормаль,
- S бетiне сыртқы нормаль,
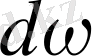 ,
,
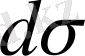 -
D
облысының көлем және
S
бетiнiң аудан элементтерi.
-
D
облысының көлем және
S
бетiнiң аудан элементтерi.
Остроградский формуласын
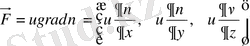
үшiн қолданайық.
Мұндағы
u
,
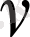 функциялары
D
облысындағы тегiс функциялар. Бiрнеше түрлендiрулерден кейiн мынадай теңдiк аламыз:
функциялары
D
облысындағы тегiс функциялар. Бiрнеше түрлендiрулерден кейiн мынадай теңдiк аламыз:
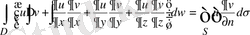 (1. 4. 6)
(1. 4. 6)
Шынында да,
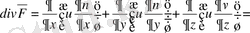
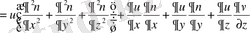
Ал
S
бетi арқылы өтетiн
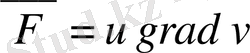 . 3 вектор ағыны, яғни
. 3 вектор ағыны, яғни
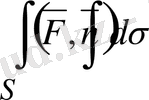 . 3
. 3
болса, ол былай өрнектеледi
өйткенi бағыт бойынша туындының қасиетi бойынша

Осындағы (1. 4. 6) формула Грин формуласы деп аталады. (Жоғарыда дәлелденген (1. 4. 1) Гриннiң бiріншi формуласы)
Бұл формулада
 және
және
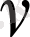 функциясы гармоникалық функция болатын етiп алса, онда
функциясы гармоникалық функция болатын етiп алса, онда
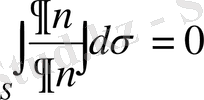 (1. 4. 7)
(1. 4. 7)
теңдiгi алынады. 1 0 қасиет дәлелдендi.
2 0 Гриннiң екiншi формуласы (1. 4. 2) -ні алайық
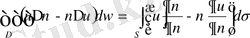
Бұл теңдiкте
 гармоникалық функция болсын да, ал
гармоникалық функция болсын да, ал
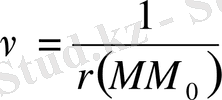 деп алайық.
деп алайық.
Мұндағы
D
облысының
 және
және
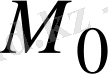 нүктелерiнiң координаталары
нүктелерiнiң координаталары
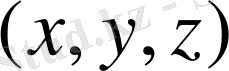 және
және
 ,
яғни
,
яғни
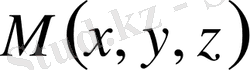 және
және
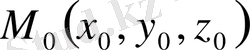 .
.
Сонда
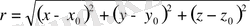
ара қашықтық формуласын жазуға болады.
Бұл
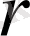 функциясы
функциясы
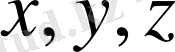 айнымалыларының гармоникалық функциясы болатындығын тексеру қиын емес. Дәлiрек айтқанда,
айнымалыларының гармоникалық функциясы болатындығын тексеру қиын емес. Дәлiрек айтқанда,
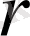 функциясы
функциясы
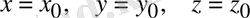 нүктелерiнде, яғни
нүктелерiнде, яғни
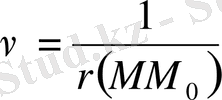 функциясы анықталмаған нүктелерден басқа нүктелердiң бәрiнде гармоникалық функция болады.
функциясы анықталмаған нүктелерден басқа нүктелердiң бәрiнде гармоникалық функция болады.
Ендi
 облысынан радиусы
облысынан радиусы
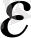 және центрi
және центрi
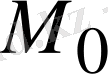 нүктесiнде болатын
нүктесiнде болатын
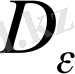 шарды шығарып тастағаннан қалған
шарды шығарып тастағаннан қалған
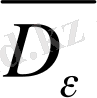 облысын қарастырайық. Бұл облыстың шекарасы
облысын қарастырайық. Бұл облыстың шекарасы
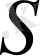 бетi мен
бетi мен
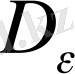 шарын қоршаған
шарын қоршаған
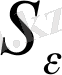 сферасының бiрiгуiнен құралған.
сферасының бiрiгуiнен құралған.
Осы
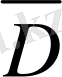 облысына (1. 4. 2) формуланы қолданайық. Сонда оның сол жағы нөлге айналады, өйткенi
облысына (1. 4. 2) формуланы қолданайық. Сонда оның сол жағы нөлге айналады, өйткенi
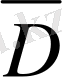 облысында
u
және
облысында
u
және
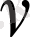 гармоникалық функциялар болады.
гармоникалық функциялар болады.
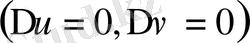 . Оң жағы екi қосылғышқа жiктеледi. Олар
. Оң жағы екi қосылғышқа жiктеледi. Олар
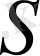 және
және
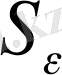 шекаралық бөлiктерiнiң интегралдауларына сәйкес келедi. Бұл жағдайда
шекаралық бөлiктерiнiң интегралдауларына сәйкес келедi. Бұл жағдайда
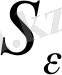 сферасының нүктелерiне
сферасының нүктелерiне
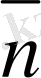 нормаль векторы сфераның iшкi жағына қарай бағытталған және
нормаль векторы сфераның iшкi жағына қарай бағытталған және
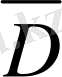 облысына сыртқы нормаль болып есептеледi. Осы талдаулар нәтижесiнде мынадай теңдiк алынады:
облысына сыртқы нормаль болып есептеледi. Осы талдаулар нәтижесiнде мынадай теңдiк алынады:
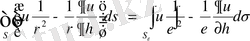 (1. 4. 8)
(1. 4. 8)
мұнда (1. 4. 7) теңдiгi бойынша
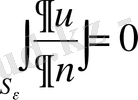 болады. Сондықтан (1. 4. 8) формула
болады. Сондықтан (1. 4. 8) формула
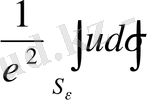 түрiнде болады да, ол орта мән туралы теорема бойынша
түрiнде болады да, ол орта мән туралы теорема бойынша
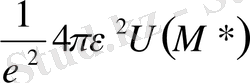 -ға тең.
-ға тең.
Мұндағы
 -
-
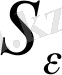 сферасының нүктесi. Егер
сферасының нүктесi. Егер
 да соңғы өрнек
да соңғы өрнек
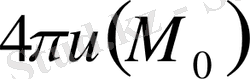 -ге ұмтылады.
-ге ұмтылады.
2-сурет
Сонымен (1. 4. 8) формуланы былай жазуға болады.
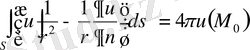 (1. 4. 9)
(1. 4. 9)
Мұндағы
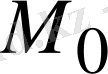 нүктесi
нүктесi
 облысының iшкi нүктесi болып табылады. Егер
облысының iшкi нүктесi болып табылады. Егер
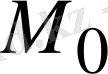 нүктесi
нүктесi
 облысының тұйықтауында жатпаса, онда (1. 4. 2) формула бойынша және
облысының тұйықтауында жатпаса, онда (1. 4. 2) формула бойынша және
 мен
мен
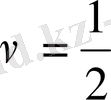 функциялары
функциялары
 облысында гармоникалық функциялар болғандықтан мына теңдiк орындалады.
облысында гармоникалық функциялар болғандықтан мына теңдiк орындалады.
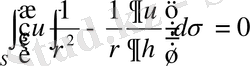
Егер
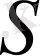 центрi
центрi
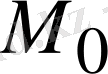 нүктесiнде, ал радиусы
нүктесiнде, ал радиусы
 сфера болса, онда (1. 4. 9) теңдiктiң сол жағындағы интегралды былай түрлендiремiз.
сфера болса, онда (1. 4. 9) теңдiктiң сол жағындағы интегралды былай түрлендiремiз.
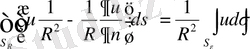
өйткенi
 гармоникалық функция болғандықтан (1. 4. 7) теңдiк орындалады. Сонымен
гармоникалық функция болғандықтан (1. 4. 7) теңдiк орындалады. Сонымен
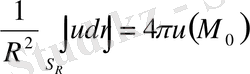
болады да, осыдан
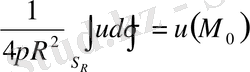 (1. 4. 10)
(1. 4. 10)
формуласы алынады.
3
0
Қарсы жориық.
 облысында
облысында
 гармоникалық функциясының мысалы максимумы
гармоникалық функциясының мысалы максимумы
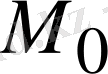 iшкi нүктесiнде қабылдансын. Онда
iшкi нүктесiнде қабылдансын. Онда
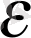 жеткiлiктi аз шамасы үшiн
жеткiлiктi аз шамасы үшiн
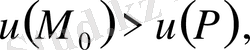
 (1. 4. 11)
(1. 4. 11)
теңсiздiгi орындалады. Мұндағы
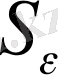 центрi
центрi
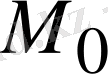 нүктесiнде болатын және радиусы
нүктесiнде болатын және радиусы
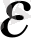 -ға тең сфера.
-ға тең сфера.
Ендi (1. 4. 10) формула және орта мән туралы теореманы пайдаланып, былай жазуға болады.
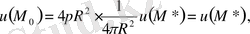

Бұл теңдiк (1. 4. 11) теңсiздiкке қайшы келедi, яғни бұл түрдегі теңсiздiк орындалмайды.
4
0
 облысында
облысында
 және
және
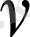 функциялары гармоникалық функциялар болсын және облыстың шекарасында
функциялары гармоникалық функциялар болсын және облыстың шекарасында

 . Онда
. Онда
 функциясы
функциясы
 облысында гармоникалық және оның
облысында гармоникалық және оның
 шекарасында тек терiс мәндер қабылдайды. Егер қандай да бiр
шекарасында тек терiс мәндер қабылдайды. Егер қандай да бiр
 iшкi нүктесiнде
iшкi нүктесiнде
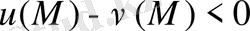 теңсiздiгi орындалатын болса, онда функцияның минимумы шекаралық нүкте болмас едi. Ол
3
0
қасиетке қайшы келедi. Бұл қайшылық
4
0
қасиеттi дәлелдейдi.
теңсiздiгi орындалатын болса, онда функцияның минимумы шекаралық нүкте болмас едi. Ол
3
0
қасиетке қайшы келедi. Бұл қайшылық
4
0
қасиеттi дәлелдейдi.
5
0
Комплекс айнымалының
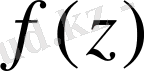 функциясы
функциясы
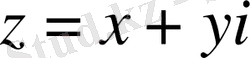 нүктесiнде аналитикалық функция болса, онда Коши-Риман шарты орындалады.
нүктесiнде аналитикалық функция болса, онда Коши-Риман шарты орындалады.
Егер
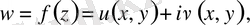
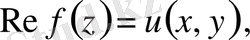
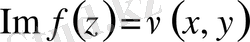
болса, онда
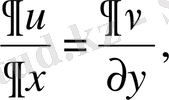
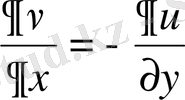 ; (Коши-Риман шарты) (1. 4. 12)
; (Коши-Риман шарты) (1. 4. 12)
Осыдан
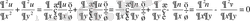
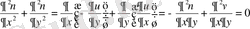
(1. 4. 12) шарттарын қанағаттандыратын екi айнымалының
 және
және
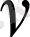 функциялары түйiндес деп аталады.
функциялары түйiндес деп аталады.
1. 5 Шеттiк есептердің шешімін анықтау
Эллиптiк типтi теңдеулер үшiн қойылған шеттiк есептердiң шешiмiн табу үшiн әртүрлi әдiстер қолданылады. Олардың iшiнде жиi қолданылатыны Фурье әдiсi, Грин функциясы әдiсi, интегралдық теңдеулер әдiсi т. б.
Кейбiр қарапайым облыстар үшiн қойылған шеттiк есептердi шешудiң Фурье әдiсiн қарастырайық.
Дөңгелек үшiн Дирихле есебiнiң шешiмiн табу.
Жазықтықта радиусы
 , центрi координаталар бас нүктесiнде болатын дөңгелек берiлсiн. Оның шеңберiнде қандай да бiр
, центрi координаталар бас нүктесiнде болатын дөңгелек берiлсiн. Оның шеңберiнде қандай да бiр
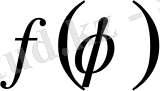 функциясы берiлсiн. Мұндағы
функциясы берiлсiн. Мұндағы
 - полярлық бұрыш. Шекарасымен қоса дөңгелектiң iшiнде үзiлiссiз және
- полярлық бұрыш. Шекарасымен қоса дөңгелектiң iшiнде үзiлiссiз және
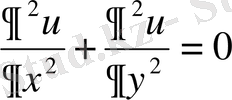 (1. 5. 1)
(1. 5. 1)
Лаплас теңдеуiн қанағаттандыратын, ал дөңгелектiң шеңберiнде берiлген мәндердi қабылдайтын, яғни
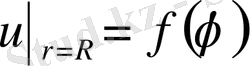 (1. 5. 2)
(1. 5. 2)
шартын қанағаттандыратын
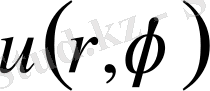 функциясын табу керек. Есептi полярлық координаталарда қарастырамыз. Полярлық координаталарында (1. 5. 1) теңдеу былай жазылады.
функциясын табу керек. Есептi полярлық координаталарда қарастырамыз. Полярлық координаталарында (1. 5. 1) теңдеу былай жазылады.
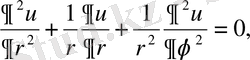
немесе,
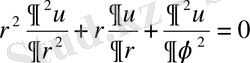 (1. 5. 1
/
)
(1. 5. 1
/
)
Шешiмдi айнымалыларды бөлу әдiсiн қолданып, мына түрде iздеймiз:
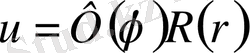 (1. 5. 3)
(1. 5. 3)
Осыны (1. 5. 1 / ) теңдеуге қоямыз
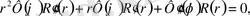
немесе
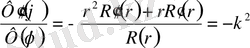 (1. 5. 4)
(1. 5. 4)
Бұл теңдiктiң сол жағы
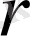 -ден тәуелсiз, ал оң жағы
-ден тәуелсiз, ал оң жағы
 тәуелсiз болғандықтан оларды тұрақты
тәуелсiз болғандықтан оларды тұрақты
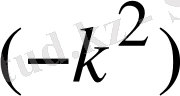 санымен белгiлеймiз. Сонда (1. 5. 4) тең қатынастардан екi теңдеу аламыз.
санымен белгiлеймiз. Сонда (1. 5. 4) тең қатынастардан екi теңдеу аламыз.
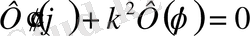 (1. 5. 5)
(1. 5. 5)
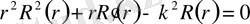 (1. 5. 6)
(1. 5. 6)
Бiрiншi (1. 5. 5) теңдеудiң жалпы шешiмi:
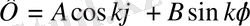 (1. 5. 7)
(1. 5. 7)
Ал (1. 5. 6) теңдеудiң жалпы шешiмiн
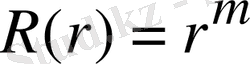 түрiнде iздеймiз. Оны (1. 5. 6) теңдеуге қойып,
түрiнде iздеймiз. Оны (1. 5. 6) теңдеуге қойып,
немесе
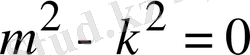
теңдеуiн аламыз. Сонда екi сызықты тәуелсiз
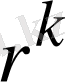 және
және
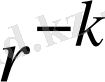 дербес шешiмдерi алынады. Олай болса, жалпы шешiм мына түрде жазылады.
дербес шешiмдерi алынады. Олай болса, жалпы шешiм мына түрде жазылады.
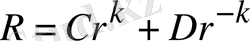 (1. 5. 8)
(1. 5. 8)
Ендi (1. 5. 7) және (1. 5. 8) өрнектердi (1. 5. 3) -ке қоямыз
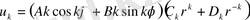 (1. 5. 9)
(1. 5. 9)
Осы (1. 5. 9) функциялар
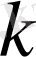 - ның нөлден өзгеше барлық мәндерiнде (1. 5. 1
/
) теңдеудiң шешiмi болады. Егер
- ның нөлден өзгеше барлық мәндерiнде (1. 5. 1
/
) теңдеудiң шешiмi болады. Егер
 болса, онда (1. 5. 5) теңдеу мына түрде жазылады:
болса, онда (1. 5. 5) теңдеу мына түрде жазылады:
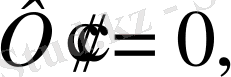
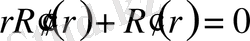
Сондықтан
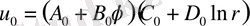 (1. 5. 9
/
)
(1. 5. 9
/
)
теңдiгiмен анықталады.
Есептiң шешiмi
 бойынша периодты функция болуы керек, яғни
бойынша периодты функция болуы керек, яғни
 бұрышы
бұрышы
 дейiн өзгергенде бiр мәндi
дейiн өзгергенде бiр мәндi
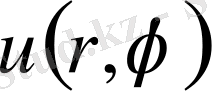 функциясы өзiнiң алғашқы мәнiне қайта келуi керек.
функциясы өзiнiң алғашқы мәнiне қайта келуi керек.
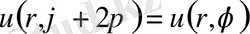
Осыдан
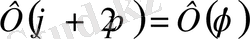 , яғни
, яғни
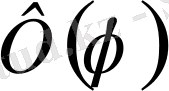 периоды
периоды
 -ге тең периодты функция болады. Олай болса (1. 5. 9
/
) теңдiгiнде
-ге тең периодты функция болады. Олай болса (1. 5. 9
/
) теңдiгiнде
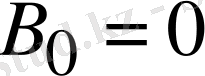 ге тең.
ге тең.
Сол сияқты шешiмнiң үзiлiссiз және шексiздiкке тең болмау шарты бойынша дөңгелектiң центрiнде
 мәнiнде шексiз шешiм алынбауы үшiн (1. 5. 9
/
) теңдiкте
мәнiнде шексiз шешiм алынбауы үшiн (1. 5. 9
/
) теңдiкте
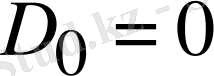 , ал (1. 5. 9) теңдiкте
, ал (1. 5. 9) теңдiкте
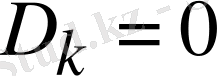 болуы талап етiледi. Сонымен (1. 5. 9
/
) теңдеудiң оң жағы
болуы талап етiледi. Сонымен (1. 5. 9
/
) теңдеудiң оң жағы
 көбейтiндiсiне тең болады да, оны
көбейтiндiсiне тең болады да, оны
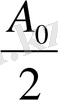 деп белгiлеймiз:
деп белгiлеймiз:
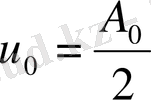
Есептiң шешiмiн (1. 5. 9) түрiндегi қосынды ретiнде құрамыз. Қосынды периодты функция болғандықтан
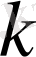 - ның бүтiн оң мәндерiмен шектелемiз. ¤йткенi терiс мәндерде жаңа дербес шешiмдер алынбайды. Осыларды ескере отырып, шешiмдi мынадай қосынды түрiнде жазамыз.
- ның бүтiн оң мәндерiмен шектелемiз. ¤йткенi терiс мәндерде жаңа дербес шешiмдер алынбайды. Осыларды ескере отырып, шешiмдi мынадай қосынды түрiнде жазамыз.
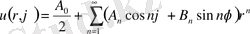 (1. 5. 10)
(1. 5. 10)
(
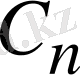 тұрақтысы
тұрақтысы
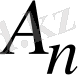 және
және
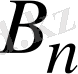 тұрақтыларының құрамына енеді. )
тұрақтыларының құрамына енеді. )
Бұл формуладағы
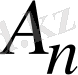 мен
мен
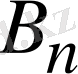 тұрақтыларын (1. 5. 2) шекаралық шартты қанағаттандыратындай етiп таңдаймыз:
тұрақтыларын (1. 5. 2) шекаралық шартты қанағаттандыратындай етiп таңдаймыз:
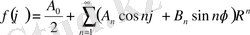 (1. 5. 11)
(1. 5. 11)
Мұндай теңдiк орындалуы үшiн
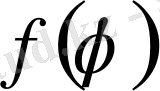 функциясы
функциясы
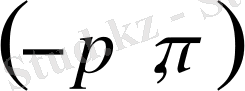 аралығында Фурье қатарына жiктелетiндей болуы керек және
аралығында Фурье қатарына жiктелетiндей болуы керек және
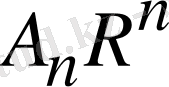 мен
мен
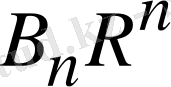 Фурье коэффициенттерi болады. Сонда
Фурье коэффициенттерi болады. Сонда
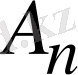 мен
мен
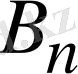 коэффициенттерi мына формулалармен анықталатын болады.
коэффициенттерi мына формулалармен анықталатын болады.
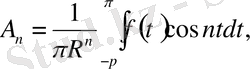
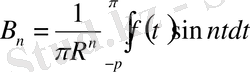 (1. 5. 12)
(1. 5. 12)
Бұл жағдайда коэффициенттерi (1. 5. 12) формулалармен анықталған (1. 5. 10) қатар қойылған есептiң шешiмi болады. Ол
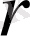 мен
мен
 бойынша екi рет дифференциалданатын функция болуы керек.
бойынша екi рет дифференциалданатын функция болуы керек.
Ендi (1. 5. 12) коэффициенттердi орнына қойып, қажеттi тригонометриялық түрлендiрулер орындағаннан кейiн мынадай өрнек аламыз:
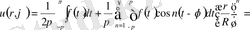
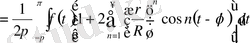 (1. 5. 13)
(1. 5. 13)
Тiк жақшаның iшiндегi өрнектi түрлендiрейiк
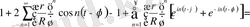

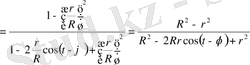
Осы өрнектi (1. 5. 13) формуладағы орнына қойып, мынадай формула аламыз
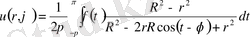 (1. 5. 14)
(1. 5. 14)
Бұл (1. 5. 14) формула Пуассон интегралы деп аталады. Анықталған
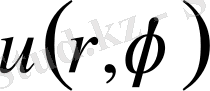 функциясы дөңгелек үшiн қойылған Дирихле есебiнiң шешiмi болып табылады.
функциясы дөңгелек үшiн қойылған Дирихле есебiнiң шешiмi болып табылады.
1-мысал:
Егер
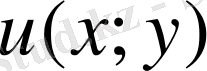 гармоникалық функциясының
гармоникалық функциясының
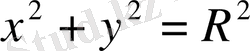 дөңгелегінің шекарасындағы мәні
дөңгелегінің шекарасындағы мәні
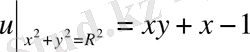
болса, онда дөңгелектiң центрiндегi мәнiн табу керек.
Шешуі: Гармоникалық функцияның мдөңгелектің центріндегі мәні осы дөңгелектiң шекарасындағы мәндерiнiң арифетикалық ортасына тең болғандықтан
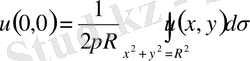
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz