Сандар теориясының элементтері және шапшаң есептеу әдістері


МАЗМҰНЫ
Кіріспе . . . 1
Негізгі бөлім
2. 1. Лезде көбейту әдістері . . .
2. 2. Кейбір бүтін сандарының бөлінгіштігі.
2. 3. Құрама және жай сан арифметиканың негізгі теоремасы. 2. 4. Ескілікті халық есептері .
Қорытынды
Қолданылған әдебиеттер
«Сандар теориясының элементтерін зерттеу. »
Кіріспе.
Қазақстан өз дамуындағы жаңа серпіліс жасау қарсаңында - деп Елбасы Нұрсұлтан Әбішұлы Назарбаев Қазақстан халқына жолдауында айтқан болатын.
Президент Қазақстанның әлемдегі бәсекеге барынша қабілетті 50 елдің қатарына кіру стратегиясын жеті басымдықтан тұратын жолдау-ында нақтылап көрсетіп берді.
Біздің заманымыз ғылым мен техниканың қарқынды дамуымен ерекшеленеді. Қазіргі көптеген мектеп оқушыларына болашақта есептеу техникасы мен автоматтық құралдармен жабдықталған цехтарда, кәсіпорындарда еңбек етуге тура келетіні сөзсіз. Жастарда жаңа техниканы басқару үшін қажетті әзірлік бар ма? Олай болса, орта мектепті оқып жүргеннің өзінде-ақ оқушылар азды-көпті шығармашыл, іздемпаз болуы шарт.
Бұл мәселелер қазір аса маңызды мәселеге айналып отыр. Мектеп оқушысының алдында тұрған міндеті-қазіргі заманғы математикалық формальды логика -кибернитикалық теорияның негізі екенін түсініп, білуі тиіс. Кибернитиканың негізін салушы әйгілі математик Н. Винер киберни-тиканың шығуының өзі математикалық логикасыз ақылға қонбас еді деп атап көрсетеді. Математикалық логика техникадағы, тірі организмдер дүниесі қоғамдық құбылыстағы аса күрделі процесстер мен құбылыстарды басқару заңдылықтары жайындағы ғылым кибернитикамен тығыз бай-ланысты. Математикалық логика ақыл-ой еңбегін техникаландырудың құралы болып табылады және ойлау процесін арнаулы математикалық әдістер, символдық аппараттар арқылы зерттейді.
Бірақ дәстүрлі математикалық логика пәнін білмейінше, оны ойда-ғыдай меңгеру қиын, өйткені бүгінгі күні ғылыми - технологияның дамуына байланысты адамзат баласы ой және дене еңбегін жеңілдететін техникалық құрылғылардың түр-түрін ойлап табуда. Мысалы, қазіргі кезде электронды есептеу машинасын қолдана отырып, кез-келген күрделі есептің шешімін аз ғана уақыт аралығында табуға болады. Тіпті, қарапайым есептеу құралы - калькуляторлардың өзі бүгінгідей нарық заманында қарапайым халық үшін аса тиімді. Әрине, мұның бәрі адамның ойлау қабілетінің ең ірі жетістіктері болып табылады.
Алайда, қалыптасқан жағдайдың пайдасымен қатар зияны да жоқ емес. Атап айтқанда, бүгінде кез-келген оқушының қарапайым көбейту кестесін біле бермеуі мүмкін. Сол себепті де, баланың логикалық ойлау қабілетін дамыту бүгінгі күннің өзекті мәселелерінің бірі деуге болады.
Сондықтан, мен, өз баяндамамның тақырыбын осы мәселерді шешудің қандай математикалық жолдары бар екендігіне, оларды орындау үшін қандай мәселелерді шешуге тура келетіндігіне, ол үшін қандай математикалық құбылыстар болытындығына арнап отырмын.
Ғылыми жұмыстың мақсаты: Аталған мәселелер туралы оқушыларға түсінікті болатындай ақпараттық мағлұматтар беру және математика-лық есептеудің кейбір әдістерін зерттеуді жүзеге асыруда әр түрлі есептердің арасында үнемі байланыс болатындығын зерттеу. Ендеше, олай болса, бұл жұмыста логикалық ойлау қабілетін дамытатын, шапшаң есептеудің кейбір әдістерін қарастырдым.
Сол себептен, бұл ғылыми жұмыстың тақырыбын былай деп атадым: «Сандар теориясының элементтерін зерттеу».
Ендеше, мен секілді математиканың ғылымилығын жаңа бастаған оқушы үшін бұл маңызды тақырып.
- Лезде көбейту әдістері.

Ғылымның дамуы шығармашылық өнермен тығыз байланысты. Шығармашылық өнер дегеніміз - күтпеген сенсациялық жаналық ойлап табу ғана емес, сонымен қатар, бұрыннан белгілі жағдайдың бұрын көңіл бөлінбеген қалтарыстарына үңілу.
Арифметика көп жағдайда өз құралдары арқылы бірқатар пайымдауларының дұрыстығын
дәлме-дәл дәлелдей алмайды.
Мұндай жағдайларда оған алгебраның
жалпылама әдістеріне сүйенуге тура келеді.
Алгебралық түрде негізделетін мұндай
арифметикалық қағидаларға, мысалы, амалдарды қысқаша орындаудың көптеген ережелері, кейбір сандардың қызықты ерекшеліктері, бөлінгіштік белгілері және басқалар жатады.
Бұл тарау осы тектес мәселелерді қарастыруға арналған.
Асқан шебер-есептеушілер көптеген жағдайларда онша күрделі емес алгебралық түрлендірулерге сүйене отырып, ездерінің есептеу жұмыс-тарын оңайлатады.
Мысалы, 988 2 санын есептеу былайша іске асырылады.
988•988= (988+12) • (988- 12) +12 2 = 1000 • 976+ 144 = = 976 144.
Есептеушінің бұл жағдайда мына алгебралық түрлендіруді пайдала-натынын аңғару оңай:
а 2 = а 2 -b 2 + b 2 =(а + b) (а-b) +b 2 .
Біз іс жүзінде бұл формуланы ауызша есептеулер үшін ойдағыдай пайдалана аламыз.
Мысалы: 27 2 =(27 + 3) (27-3) +3 2 = 729,
63 2 = 66•60 + 3 2 = 3969,
18 2 = 20•16 + 2 2 = 324,
37 2 = 40•34 + 3 2 =1369,
48 2 = 50•46+2 2 = 2304,
54 2 = 58•50+4 2 = 2916.
Бұдан кейін 986 • 997 көбейту былайша орындалады:
986 • 997= (986-3) • 1000 + 3 • 14= 983042.
Бұл тәсіл неге негізделген?
Көбейткіштерді мына түрде жазалық, (1000-14) • (1000-3)
және осы екімүшелерді алгебра ережесі бойынiа көбейтелік:
1000 • 1000-1000 • 14-1000 • 3+14-3.
Мұны түрлендірейік:
1000(1000-14) -1000•3 + 14•3 = 1000•986-1000•3 +14•3= −1000(986-3) +14•3.
Соңғы жол есептеушінің қолданған тәсілін кескіндейді.
Ондықтарының саны бірдей, ал бірақ цифрларының қосындысы 10 бола-тын үш таңбалы екі санды өзара көбейту тәсілі қызықты.
Мысалы, 783•787 көбейту былайша орындалады:
78•79 = 6162; 3•7 = 21; нәтижесі: 616 221.
Бұл тәсілді негіздеу мына түрлендірулерден айқын көрінеді:
(780 + 3) (780 + 7) =780 • 780 + 780 • 3 + 780 • 7+3 • 7 =
= 780 • 780 + 780 • 10 + 3 • 7 = 780(780+ 10) +3 • 7 =
= 780 • 790 + 21 = 616 200 + 21.
Осыған ұқсас көбейтуді орындауға арналған мына бір әдіс бұдан да оңай:
783 • 787= (785-2) (785 + 2) = 785 2 -4 = 616 225-4 = 616221.
Бұл мысалда біздің 785 санын квадрат дәрежеге шығаруымызға тура келеді.
5-пен аяқталатын сандардың квадрат дәрежесін тез табу үшін, мына тәсіл өте ыңғайлы: 35 2 ; 3•4=12. Жауабы 1225.
5 2 ; 6•7 = 42. Жауабы 4225.
75 2 ; 7•8 = 56. Жауабы 5625.
Бұл ереже бойынша ондықтар саны өзінен бір бірлікке артық санға көбейтіліп, осы кебейтіндіге 25 саны тіркеліп жазылады.
Бұл әдіс мынаған негізделген:
Егер ондықтар саны а болса, онда барлық санды былай жазьш көрсетуге болады: 10 a +5.
Бұл санның квадраты екімүшенің квадраты болғандықтан мынаған тең: 100а 2 +100а+25= 100 а ( а +1) +25.
а(а+1) өрнегі - ондықтар санының ең жақын жоғары санға көбейтіндісі. Санды 100-ге көбейтіп, оған 25-ті қосу - санға 25-ті тірrеп жазумен бірдей.
Осы әдістен бүтіннен және
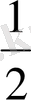 -ден құралған санды квадрат дәрежеге шығарудың қарапайым тәсілі шығады. Мысалы:
-ден құралған санды квадрат дәрежеге шығарудың қарапайым тәсілі шығады. Мысалы:
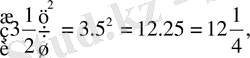
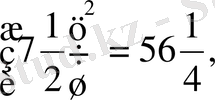
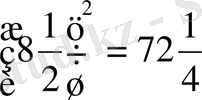 т. с. с.
т. с. с.
1, 5 және 6 цифрлары
Бірмен не беспен аяқталатын бірқатар сандарды көбейткенде, сол цифрлармен аяқталатын сандардың шығатынын барлығын байқаған боларсыңдар. Осы айтылған жайттың 6 санына да қатысы болатыны онша белгілі емес. Сондықтан, былайша айтқанда, алтымен аяқталатын санның кез келген дәрежееі де алтымен аяқталады.
Мысалы, 46 2 = 2116; 46 3 = 97 336.
1, 5 және 6 цифрларының осы қызғылықты ерекшелігін алгебралық жолмен негіздеуге болады. Мұны 6 цифры үшін қарастырайық.
Соңы алтымен аяқталатын сан былай өрнектеледі:
10а+6, 10 b + 6 т. с. с,
мұндағы а және b - бүтін сандар.
Мұндай екі санның көбейтіндісі мынаған тең:
100а b + 60 b + 60 a + 36=10(10 аb +66 + 6 a ) +30 + 6=10(10 ab + 6 b + 6 a + 3) +6.
Көбейтіндінің кез келген ондықтар санынан және санның соңында тұруға тиісті 6 цифрынан құралатынын байқаймыз.
Дәлелдеудің осы тәсілін 1 және 5 сандарына да қолдануға болады.
Осы айтылған жайт біздің былайша пайымдауымызға мүмкіндік береді, мысалы,
386 2567 -сі 6-мен аяқталады,
815 723 -сі 5-пен -»-
491 1732 -сі 1-мен -»- т. с. с.
25 және 76 сандары
1, 5 және 6 сандарының қасиеттері сияқты қасиеттерге ие болатын екі таңбалы сандарда бар. Бұлар - 25 саны мен, сірә, қөбіңді таң қалдыратын, 76 саны. 76 санымен аяқталатын кез келген екі санның көбейтіндісінен 76 санымен аяқталатын сан шығады. Мұны дәлелдейік. . Бұған ұқсас сандардың өрнегі мынадай болады:
100 a + 76, 100 b + 76 т. с. с.
Осы түрдегі екі санды өзара көбейтеміз, сонда мынау шығады:
1 ab + 7600 b + 7600 а + 5776= 10 000 аb + 7600 b + 7600 а + 5700 + 76=
=100 (100 ab + 76 b + 76 а + 57) +76.
Көбейтіндінің 76 санымен аяқталатыны дәлелденді. Бұдан 76-мен аяқталатын санның кез келген дәрежесі сондай санмен аяқталатыны шығады: 376 2 =141376, 576 3 = 191 102 976 т. с. с.
Шексіз «сандар»
Сандардың соңында тұрып, олардың көбейтіндісінде де сақталатын тым ұзақ цифрлар тобы да бар. Біз мұндай цифрлар тобының шексіз көп екенін көрсетеміз.
Біз мұндай қасиеті бар екі таңбалы цифрлар тобын білеміз: олар 25 пен 76. Үш таңбалы цифрлар тобын табу үшін 25 немесе 76 санының алдына, шығатын үш таңбалы цифрлар тобы да қажетті қасиетке ие болатындай, бір санды тіркеп жазу керек.
76 санына қандай цифрды тіркеп жазу керек. Ол санды k арқылы белгілейік. Cонда ізделінді үш таңбалы сан былай кескінделеді:
100 k + 76.
Осындай цифрлар тобымен аяқталатын сандардың жалпы өрнегінің түрі мынадай болады:
1000 а +100 k + 76, 1000 b +100 k +76 т. с. с.
Осы түрдегі екі санды өзара көбейтеміз; сонда мынау шығады:
1 000 000 аb +100 000 аk +100 000 bk + 76 000 а +
+76 000 b +10 000 k 2 +15200 k + 5776.
Соңғы екі қосылғыштан өзге қосылғыштардың бәрінің соңында кемінде үш нөлден бар. Сондықтан егер мына айырма
15 200 k + 5776 -(100 k +76) = 15 100 k + 5700 =
= 15 000 k -5000+100( k + 7)
1000-ға бөлінсе, онда көбейтінді 100 k +76 санымен аяқталады. k = 3 болғанда ғана, сірә, солай болар. Сонымен, ізделінді цифрлар тобының түрі мынадай болады: 376. Сондықтан 376 санының кез келген дәрежесі де 376 санымен аяқталады. Мысалы:
376 2 =141376.
Егер де енді біз сондай қасиеті бар төрт таңбалы цифрлар тобын тапқымыз келсе, онда 376 санының алдына тағы бір цифрды тіркеп жазамыз. Осы цифрды l арқылы белгілесек, мынадай есепті шығарамыз:
(10 000 а +1000 l +376) (10 000 b + 1000 l + 376)
көбейтіндісі l -дің қаyдай мәнінде 1 l +376 санымен аяқталады? Егер осы көбейтіндінің жақшаларын ашып, 4 және одан да көбірек нөлдермен аяқталатын қосындылардың барлығын шығарып тастасақ, онда мынадай мүшелер қалады: 752 000 l +141376.
Егер 752 000 l +141 376−(1000 l +376) =751000 l + +141 000=
=(750 000 l +140 000) + 1000( l +1)
айырма 10 000-ға бөлінсе, онда көбейтінді 1000 l +376 санымен аяқталады. l = 9 болғанда ғана, сірә солай болap.
Ізделген төрт таңбалы цифрлар тобы - 9376. Осы шыққан төрт таңбалы цифрлар тобын тағы да бір цифрмен толықтыруға болады, бұл үшін дәл жоғарыдағыдай пайымдау жасау керек. Сонда 09 376 шығады. Тағы да бір қадам жасап, 109 376 цифрлар тобын табамыз, сонан соң
7 109 376 т. с. с.
Цифрларды сол жаққа осылайша шексіз сан есе тіркеп жазуға болады. Осының нәтижесінде шексіз көп цифрлары бар мынадай «сан» шығады:
. . . 7 109 376.
Осы тәрізді «сандарды» әдеттегі ереже бойынша қосуға және көбейтуге болады: себебі Олар оңнан солға қарай жазылады, ал қосу мен көбейту («баған түрінде») де оңнан солға қарай орындалады, осындай екі санды қосу мен көбейту кезінде бір цифрдан соң екіншісін неше цифр болса да қажетінше есептеп таба беруге болады.
Жоғарыда жазылған шексіз «санның» таң қаларлық болып көрінген-мен мына х 2 = х теңдеуін қанағаттандыратыны қызықты жайт.
Шынында осы «санның» квадраты (яғни мұның өз-өзіне көбейтіндісі)
76-мен аяқталады, себебі көбейткіштердің әрбіреуі 76 санымен аяқталады; жазылған «санның» квадраты 376-мен аяқталатыны сол себепті т. с. с. Басқаша айтқанда, х 2 (мұндағы х = . . . 7 109 376) «санының» цифрларын бірінен кейін бірін есептей отырып, біз х санында бар цифрларды шығарып аламыз, сол себептен х 2 =х
Біз 76-мен аяқталатын цифрлар тобын қарастырдық .
Егер 5-пен аяқталатын цифрлар тобы үшін осындай пайымдаулар жасала-тын болса, онда біз мынадай цифрлар тобын шығарып аламыз:
5, 25, 625, 0625, 90 625, 890 625, 2 890 625 т. с. с
Осының нәтижесінде біз тағы бір шексіз «санды» жаза аламыз:
. . . 2 890 625,
бұлда х 2 =х теңдеуін қанағаттандырады. Осы шексіз «санның» мынаған «тең» екенін дәлелдеуге болады: ( ( (5 2 ) 2 ) 2 ) 2 ···
Осы шыққан қызықты нәтиже шексіз «сандар» тілінде былайша тұжырымдалады: х 2 =х теңдеуінің «шектеусіз» екі шешімі бар .
(әдеттегі х=0 және х =1-ден басқа) : х = . . . 7109376 және х= . . . 2890625,
ал басқа шешімі (ондық санау жүйесінде) жоқ .
2. 2. Кейбір бүтін сандарының бөлінгіштігі.
11-ге бөлінгіштік
Алгебра бөлу амалын орындамай-ақ, берілген санның қай бөлгішке бөлінетінін, қайсысына бөлінбейтінін • алдын ала анықтауға болатын белгілерді табуды едәуір жеңілдетеді. 2-ге, 3-ке, 4-ке, 5-ке, 6-ға, 8-ге, 9-ға және 10-ға бөлінгіштік белгілері баршамызға мәлім. 11-ге бөлінгіштік белгісін қорытып шығарайық; ол едәуір қарапайьш әрі қолайлы.
Көп таңбалы N санының бірлік цифры а, ондық цифры b, жүздік цифры с, мыңдық цифры d болсын т. с. с, яғни
N=a+10b+100c+1000d+…=a+10(b+10c+100d+…),
Мұндағы көп нүкте келесі разрядтардың қосындыларын білдіреді. N санынан 11-ге еселік болатын 11(b+10c+100d+…) санын шегереміз. Сонда шыққан айырма мынаған тең болады:
a−b−10(c+10d+…),
бұл санды 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болатынын байқау оңай. Осы айырмаға 11-ге еселік болатын
11(с+10d + . . . ), санын қосып, мынадай сан шығарып аламыз:
a−b+c+10(d+…),
мұны да 11-ге бөлгенде қалатын қалдық N санынан қалатын қалдықтай болады. Бүдан 11-ге еселік болатын 11( d + . . . ) санын шегереміз, т. с. с. Осының нәтижесінде мынадай сан шығады:
a-b+c-d+…=(a+c+…) -(b+d+…),
мұны да 11-ге бөлгенде қалатын қалдық бастапқы N санынан қалатын қалдықтай болады.
Осыдан 11 -ге бөлінгіштіктің мынадай белгісі шығады: барлық тақ орындардағы цифрлардың қосындысынан барлық жұп орындардағы цифрлардың қосындысын шегеру керек: егер осы айырмадан 0 немесе
11-ге еселік болатын сан (оң немесе теріс) шықса, онда сыналатын санымыз 11-ге еселік болады; олай болмаған жағдайда әлгі сан 11-ге қалдықсыз бөлінбейтін болады. Мысалы, 87 635 064 санын сынайық:
84-6 + 5 + 6 = 25,
7 + 3+0 + 4= 14,
25-14=11.
Олай болса, бұл сан 11-ге бөлінеді.
11-ге бөлінгіштіктің басқа да бір белгісі бар, бұл өте ұзақ созылып жазылмаған сандар үшін қолайлы. Бұл белгі бойынша саналатын сан оңнан солға қарай екі-екі цифрдан топталып, ажыратылады да, бұл топтарды өзара қосады. Егер осы шыққан қосынды 11-ге қалдықсыз бөлінетін болса, онда саналушы сан 11 -ге еселік болады, олай болмаған жағдайда - ол 11-ге есе-лік болмайды. Мысалы, 528 санын сынау керек болсын дейік. Санды топ-топқа ажыратамыз да (5/28), екі топты өзара қосамыз:
5+28 = 33.
33 саны 11-ге қалдықсыз бөлінетін болғандықтан, 528 саны да 11-ге еселік болады:
528:11=48.
Осы бөлінгіштік қасиетін дәлелдейік. Көп таңбалы N санын топтарға ажыратайық. Сонда екі таңбалы (немесе бір таңбалы') сандар шығады, оларды а, b, с т. с. с. арқылы (оңнан солға қарай) белгілейміз, сонда N санын мына түрде жазуға болады:
N=a+100b+1c+…=a+b+100(c+…)
N -нен он бірге еселік болатын 99( b + 100с+- . . . ) санын шегереміз. Бұдан шыққан а+(b +100 c+ . . . ) = а + b + 100(с+ . . . )
санын 11-ге бөлгенде шығатын қалдық N санынан қалатын қалдықтай болады. Осы соңғы саннан 11-ге еселік болатын 99(с+ . . . ) санын шегереміз т. с. с. Осының нәтижесінде біз N санын 11-ге бөлгенде қалатын қалдық а+b + с+ . . . санынан қалатын қалдықтай болатынын табамыз.
19-ға бөлінгіштік
19-ға бөлінгіштіктің мына белгісін негіздеңдер. Санның ондықтарының саны мен оның екі еселенген бірліктерінің қосындысы 19-ға еселік болғанда, тек сонда ғана ол сан 19-ға қалдықсыз бөлінеді.
ШЕШУІ
Кез келген N санын мына түрде өрнектеп көрсетуге болады:
N=10х+у,
мұнда х - ондықтардың саны (ондық разрядтағы ц и ф р емес, сандағы барлық бүтін ондықтардың жалпы саны), у - бірліктер цифры.
N'=х + 2у
саны 19-ға еселік болғанда, тек сонда ғана N санының 19-ға еселік болатынын көрсетуіміз керек. Бұл үшін N'- ты 10-ға көбейтеміз де, осы көбейтіндіден N -ді шегереміз; сонда шығатыны
10 N '- N = 10(х + 2у) - (10х + у) =19у.
Бұдан, егер N' саны 19-ға еселік болса, онда
N= 10 N '- 19у
саны 19-ға қалдықсыз бөлінеді: және, керісінше, егер N саны 19-ға қалдықсыз бөлінетін болса, онда
N ' = N+19у
саны 19-ға еселік болады, сонда N ' саны да 19-ға қалдықсыз бөлінеді.
Мысалы, 47 045 881 саны 19-ға бөліне ме, жоқ па соны анықтау керек болсын. Өзімізге мәлім бөлінгіштік белгісін ретімен қолданайық:

19 саны 19-ға қалдықсыз бөлінетіндіктен, 57, 475, 4712, 47 063, 470 459, 4 704 590, 47 045 881 сандары да 19-ға еселік болады.
Сонымен, біздің санымыз 19-ға бөлінеді.
2. 3. Құрама және жай сан арифметиканың негізгі теоремасы.
Жай сандардың саны.
Тізбектес құрама сандардың мейлінше ұзақ тізбектерінің болатындығы жай сандар қатарының шексіз екені Шынымен рас па деген күмән тудырады. Сондықтан да жай сандар қатарының шексіз екендігінің дәлелдемееін келтіргеніміз бұл жерде артық болмас.
Бұл дәлелдеме ежелгі грек математигі Евклидке тән және оның әйгілі «Бастамалар» деген кітабына енген. Ол дәлелдеу «қарама-қарсы жорулар» қатарына жатады. Жай сандар қатары шектеулі деп ұйғарайық та, бұл қатардағы ең соңғы жай санды N әрпімен белгілеп көбейтінді құрайық:
1 •2 •3•4•5•6•7• . . . • N = N !
және оған 1-ді қосайық, сонда мынау шығады:
N! + 1.
Бұл сан - бүтін сан болғандықтан, оның ең болмағанда бір жай көбейткіш болуы, яғни ең болмағанда бір жай санға бөлінуі тиіс. Ұйғаруымыз бойынша, барлық жай сандар N -нен артық емес, N! +1 саны болса, N -нен кіші немесе оған тең бірде-бір санға қалдықсыз бөлінбейді, әр жолы 1 қалдық қалады.
Сонымен, жай сандар қатарын шектеулі деп ұйғаруға болмайды екен, мұндай жорамал қарама-қайшылыққа әкеп соқтырады. Сондықтан біз натурал сандар қатарынан тізбектес құрама сандардың қандай тізбегін кездестірсек те, одан кейін тағы да шексіз көп жай сандар жиыны табылатынына көзіміз жетуі керек.
Бізге белгілі ең үлкен жай сан
Жай сандардың мейлінше көп болатынына көзіміз жеткені бір мәселе болса, ал қандай сандардың жай сандар болып табылатынын білу екінші мәселе. Натурал сан қаншалықты үлкен болған сайын, оның жай сан болатын-болмайтынын анықтау үшін соншалықты көп есептеулер орындауға тура келеді. Қазіргі кезде белгілі ең үлкен жай сан мынау: 2 2281 −1
Бұл санда жеті жүзге жуық ондық таңба бар. Осы санның жай сан бола-тындығын анықтаған есептеулер осы заманғы есептеуіш машиналармен жүргізілді (I, II тарауларды қара) .
Құрама сандар
Жай сандар деп аталатын сандар, яғни бір мен өзінен басқа ешбір бүтін сандарға қалдықсыз бөлінбейтін, бірден үлкен бүтін сандар шексіз көп.
Бұл сандардың қатары 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . . . сандарымен басталып, олардың қатары шексіз жалғаса береді. Бұлар құрама сандардың арасына сыналанып кіріп, натурал сандар қатарын құрама сандар тізбектеріне бөледі. Бұл тізбектердің ұзындығы қандай болады?
Мысалы мыңдаған құрама сандар бірде-бір жай санмен жігін ажырат-пай, қатарынан тізіліп кездесе ме?
Шындыққа жанаспайтындай болып көрінгенмен жай сандар ара-сындағы құрама сандар тізбектері түрліше бола береді. Олар мыңдаған, миллиондаған, триллиондаған т. с. с. құрама сандардан түзілуі мүмкін.
Қолайлы болу үшін шартты п ! символын пайдаланамыз, бұл символ, 1-ден бастап п -ге дейін ( п -ді қоса алғанға дейінгі) барлық сандардың кебейтінділерін білдіреді. Мысалы 5!=1 • 2 • 3•4 • 5.
Біз енді мына қатардың
[(п+1) ! + 2], [(п+1) ! + 3], [(п+1) ! + 4], . . . [(п+1) ! + п+1]
өрнегіне дейін тізбектелген п құрама саннан тұратынын дәлелдейік.
Бұл сандар натурал қатарда бірінен соң бірі тікелей келіп отырады, себебі әрбір санның өзінің алдындағы саннан 1-уі артық. Бұлардың барлығының құрама сан екенін дәлелдеу ғана қалды.
Бірінші сан (п+1) !+ 2=1•2•3•4•5•6•7• . . . • (п+1) +2 жұп, себебі оның екі қосылғышында да 2 көбейткіші бар.
2-ден үлкен кез келген жұп сан -құрама сан.
(п +1) !+3=1•2•3•4•5 • . . . • (п+1) +3
әрқайсысы 3-ке еселік болатын екі қосылғыштан тұрады.
Олай болса, бұл да қүрама сан. Үшінші сан
(п +1) !+4=1•2•3•4•5 • . . . • (п+1) +4
4-ке қалдықсыз белінеді, себебі ол 4-ке еселік болатын қосылғыш-тардан тұрады.
Осыларға ұқсас мына санның
(п+1) !+5
5-ке еселік болатынын анықтаймыз т. с. с. Басқаша айтқанда, біз мысал-ға алған қатардың әрбір санында 1-ден және оның өзінен басқа көбейткіш бар; олай болса, құрама сан болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz