Кез келген күштер жүйесін келтіру: Пуансо леммасы, бас вектор пен бас момент және тепе-теңдік шарттары


V ТАРАУ
хочу наверх
§ 5. 1 Күшті берілген центрге келтіру
Әсер сызықтары кеңістікте (жазықтықта) кез-келген түрде орналасқан күштерден құралған жүйе кеңістіктегі (жазықтықтағы) кез-келген күштер жүйесі делінеді. Кез-келген күштер жүйесі әсеріндегі дене жағдайын немесе тепе-теңдігін зерттеу үшін осы күштер қарапайым түрге келтіріледі.
Пуансо леммасы. Күшті бір нүктеден берілген центрге келтіру нәтижесінде келтіру центрінде осы күшке тең болатын күш және оның қосылған жұбы алынады.
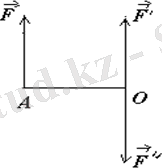
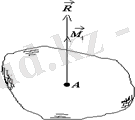
Дәлелі. Айталық, дененің А нүктесіне
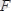 күш қойылған болсын (5. 1 сурет) . Бұл күшті кезкелген О нүктеге параллель көшіру үшін 3 аксиомаға сәйкес осы нүктеге
күш қойылған болсын (5. 1 сурет) . Бұл күшті кезкелген О нүктеге параллель көшіру үшін 3 аксиомаға сәйкес осы нүктеге
 күшті қоямыз (5. 1 сурет) .
күшті қоямыз (5. 1 сурет) .
 Мұнда
Мұнда
 .
.
Нәтижеде:
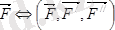 ,
,
немесе
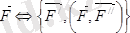 .
.
5. 1 сурет Мұндағы
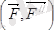 қосылған жұп делінеді. Осы күштің моменті (4. 2) -ге сәйкес төмендегідей болады:
қосылған жұп делінеді. Осы күштің моменті (4. 2) -ге сәйкес төмендегідей болады:
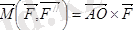 немесе
немесе
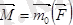 .
.
Демек:
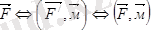 .
.
Осымен лемма дәлелденеді.
§ 5. 2 Кез-келген күштер жүйесін берілген центрге келтіру
Айталық, денеге
 күштер қойылған болсын. Жоғарыдағы тақырыпқа негізделіп, Пуансо леммасын қолданамыз (5. 2 сурет) .
күштер қойылған болсын. Жоғарыдағы тақырыпқа негізделіп, Пуансо леммасын қолданамыз (5. 2 сурет) .
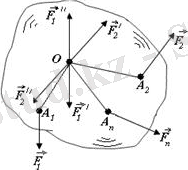
5. 2 сурет. 5. 3 сурет
Нәтижеде О нүктеде
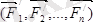 күштер және
күштер және
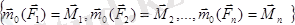 қосылған жұптар пайда болады. Егерде
қосылған жұптар пайда болады. Егерде
 күштердің әсер сызықтары кеңістікте болса,
күштердің әсер сызықтары кеңістікте болса,
 жұп моменттерінің векторлары геометриялық; жазықтықта болса, алгебралық қосылады.
жұп моменттерінің векторлары геометриялық; жазықтықта болса, алгебралық қосылады.
 күштер қиылысатын күштер жүйесі болғандықтан олар геометриялық қосылады.
күштер қиылысатын күштер жүйесі болғандықтан олар геометриялық қосылады.
Нәтижеде:
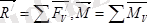 (5. 1)
(5. 1)
Мұнда
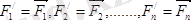 болғандықтан (5. 1) -ді төмендегідей жазу мүмкін:
болғандықтан (5. 1) -ді төмендегідей жазу мүмкін:
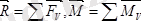 (5. 2)
(5. 2)
Кезкелген күштер жүйесі жазықтықта орналасқан болса, (5. 2) -ні былай жазамыз:
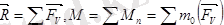 (5. 3)
(5. 3)
(5. 2) және (5. 3) өрнектердегі
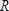 күштер жүйесінің бас векторы, ал
күштер жүйесінің бас векторы, ал
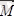 бас моменті делінеді.
бас моменті делінеді.
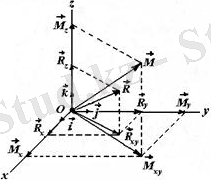
Демек, кезкелген күштерді берілген центрге келтіру нәтижесінде бір бас вектор және бір бас момент алынады (5. 3 сурет) .
Бас вектор және бас моментті аналитикалық тәсілде төмендегідей есептеу мүмкін.
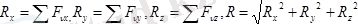 (5. 4)
(5. 4)
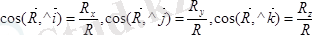 (5. 5)
(5. 5)
Бас вектор мен бас момент арасындағы бұрышты анықтау үшін бұл векторларды скаляр көбейтеміз:
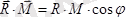 .
.
Немесе
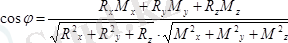 (5. 6)
(5. 6)
келіп шығады.
§ 5. 3 Кез-келген күштер жүйесін қарапайым түрге келтіру
Кезкелген күштерді қарапайым түрге келтіру үшін төмендегі жағдайларды қарастырамыз:
1. Бас вектор
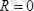 , бас момент
, бас момент
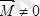 болса, кезкелген күштер жүйесі бір бас моментке келтіріледі.
болса, кезкелген күштер жүйесі бір бас моментке келтіріледі.
2. Егер бас момент
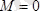 , бас вектор
, бас вектор
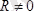 болса, күштер жүйесі бас векторға келтіріледі.
болса, күштер жүйесі бас векторға келтіріледі.
3. Бас вектор
 және бас момент
және бас момент
 болып, олар өзара
болып, олар өзара
 перпендикуляр болғанда, кезкелген күштер жүйесі бір бас векторға келтіріледі.
перпендикуляр болғанда, кезкелген күштер жүйесі бір бас векторға келтіріледі.
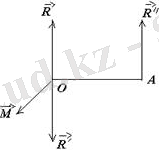 Шынында да, бұл жағдайдың дұрыстығын көрсету үшін бас момент құраушыларын сондай өзгертеміз, нәтижеде
Шынында да, бұл жағдайдың дұрыстығын көрсету үшін бас момент құраушыларын сондай өзгертеміз, нәтижеде
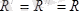 болып, ал
болып, ал
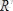 бас вектор
бас вектор
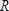 бағытталған сызық бойымен қарама-қарсы бағытталсын (5. 4 сурет) .
бағытталған сызық бойымен қарама-қарсы бағытталсын (5. 4 сурет) .
Бұл жағдайда
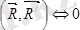 болып, О нүктеде АО=М/R қашықтықта
болып, О нүктеде АО=М/R қашықтықта
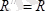 орналасады. Демек, А нүктеде бір бас вектор алынады.
орналасады. Демек, А нүктеде бір бас вектор алынады.
5. 4 сурет
1. Бас вектормен бас момент бір түзу бойында орналасса, бұл жағдай динамо (динамикалық винт) делінеді.
Бас вектор және бас момент нөлге тең болмаса және олар бір-біріне перпендикуляр болмаса, онда мұндай күштер жүйесі динамоға келтіріледі.
Бұның дұрыстығын көрсету үшін бас моментті құраушыларға жіктейміз. Бұл құраушылардын бірі бас вектор бойымен, екіншісі бас векторға перпендикуляр болсын (5. 5 сурет) .
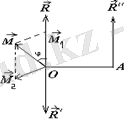 5. 5 сурет 5. 6 сурет
5. 5 сурет 5. 6 сурет
Енді
 мен
мен
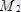 - ге 3 жағдайды қолдансақ,
О
нүктеден
- ге 3 жағдайды қолдансақ,
О
нүктеден
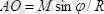 қашықтықта бас вектор
қашықтықта бас вектор
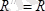 алынады. Сонымен, кезкелген күштер жүйесі
О
нүктедегі моменті
алынады. Сонымен, кезкелген күштер жүйесі
О
нүктедегі моменті
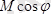 болатын
болатын
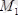 жұп моменті векторына және
А
нүктедегі бас векторға келтіреді. Жұп моментінің векторы еркін болғаны үшін
жұп моменті векторына және
А
нүктедегі бас векторға келтіреді. Жұп моментінің векторы еркін болғаны үшін
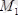 -ді А нүктеге көшіру мүмкін. Демек, күштер жүйесі динамоға келтірілді (5. 6 сурет) .
-ді А нүктеге көшіру мүмкін. Демек, күштер жүйесі динамоға келтірілді (5. 6 сурет) .
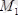 және
және
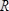 векторлар бағытталған ось центрлік винт өсі делінеді.
векторлар бағытталған ось центрлік винт өсі делінеді.
Бас вектор және бас момент нөлге тең болса, кезкелген күштер жүйесі тепе-теңдікте болады.
Есеп 5. 1
Қырының ұзындығы а= 10 см кубке, 5. 7 суретте көрсетілгендей, шамалары F= 10 н . бірнеше күш қойылған. Осы күштер жүйесі қарапайым түрге келтірілсін.
Шешуі. Координата басы ретінде А нүктесін қабылдап, Ax, Ay, Az өстерін өткізейік. Күштердің денеге қойылған нүктелерінің координаталарын анықтайық, яғни
 ;
;
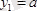 ;
;
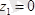 ;
;
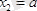 ;
;
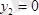 ;
;
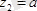 ;
;
 ;
;
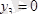 ;
;
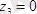 ;
;
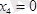 ;
;
 ;
;
 ;
;
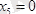 ;
;
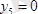 ;
;
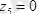 .
.
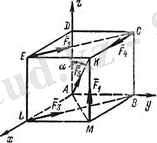
5. 7 сурет
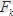 күштерінің координат өстеріне болған проекцияларын табайық
күштерінің координат өстеріне болған проекцияларын табайық
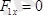 ;
;
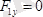 ;
;
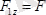 ;
;
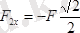 ;
;
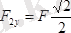 ;
;
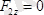 ;
;
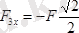 ;
;
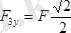 ;
;
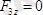 ;
;
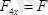 ;
;
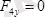 ;
;
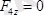 ;
;
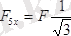 ;
;
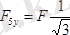 ;
;
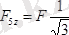 .
.
 күшінің өстерге болған проекцияларын анықтау үшін оны алдын-ала
AD
және
АМ
бағыттарына жіктеп алдық. Егер
күшінің өстерге болған проекцияларын анықтау үшін оны алдын-ала
AD
және
АМ
бағыттарына жіктеп алдық. Егер
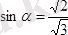 ;
;
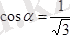 .
.
екендігін еске алсақ, онда бас вектордың координат өстеріне болған проекциялары
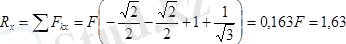 н;
н;
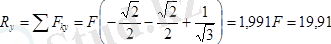 н;
н;
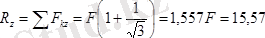 н.
н.
болады.
Денеге әсер ететін күштер жүйесінің бас моментінің өстерге болған проекциялары
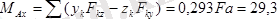
 ;
;
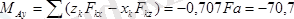
 ;
;
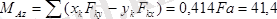
 .
.
тең.
Демек денеге қойылған күштер жүйесінің бас векторы мен оның бас моменті нөлге тең емес. Олай болса бас вектор мен бас моменттің (екінші инвариант) скаляр көбейтіндісі
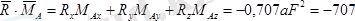
 .
.
болады.
Бұдан
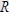 және
және
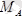 векторлары бір біріне перпендикуляр еместігі көрінеді. Бұл жағдайда күштер жүйесі динамикалық винтке келтіріледі. Динамикалық винт өсінің теңдеуі төмендегідей көрініске ие
векторлары бір біріне перпендикуляр еместігі көрінеді. Бұл жағдайда күштер жүйесі динамикалық винтке келтіріледі. Динамикалық винт өсінің теңдеуі төмендегідей көрініске ие
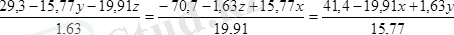 .
.
Динаманың параметрі
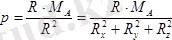 .
.
формуламен анықталады.
Мұның сан мәні
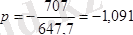 см.
см.
болады.
§ 5. 4 Кез-келген күштер жүйесінің тепе-теңдік шарттары
Кеңістікте орналасқан кезкелген күштер жүйесі әсеріндегі дене тепе-теңдікте болуы үшін күштердің бас векторы және бас моменті нөлге тең болуы қажетті және жеткілікті:
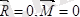 (5. 7)
(5. 7)
(5. 7) ні Декарт координат өстеріне проекциялаймыз:
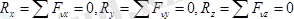 ; (5. 8)
; (5. 8)
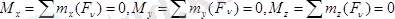 .
.
Кезкелген күштер жазықтықта орналасқан болса, олардың тепе-теңдік шарты төмендегідей болады:
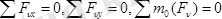 (5. 9)
(5. 9)
Егерде күштер жүйесі кеңістікте (жазықтықта) қиылысатын күштерден құралған болса, олардың тепе-теңдік шарттары сәйкес түрде былай жазылады:
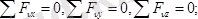 (5. 10)
(5. 10)
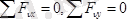 (5. 11)
(5. 11)
Кезкелген күштер жүйесі Oz өсіне параллель болса, (5. 10) -ның алғашқы екеуі және соңғысы тікелей нөлге тең болады. Нәтижеде кеңістіктегі параллель тепе-теңдігінің шарты төмендегідей болады:
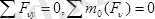 (5. 12)
(5. 12)
Мұндағы күштер Оу осіне параллель.
§ 5. 5 Әртүрлі күштер әсеріндегі дененің тепе-теңдік шарттарының кестесі
Бақылау сұрақтары.
1. Пуансо леммасы қалай баяндалады?
2. Кезкелген күштерді бір центрге келтіруді түсіндіріңіз.
3. Бас вектор және бас момент не?
4. Қай жағдайда кезкелген күштер жүйесі бас векторға келтіріледі?
5. Қай жағдайда кезкелген күштер жүйесі бас моментке келтіріледі?
6. Динамо не ?
7. Тең әсерлі күштің бағыттаушы косинустары қалай анықталады?
8. Бас моменттің бағыттаушы косинустары қалай табылады?
9. Бас момент пен бас вектор арасындағы бұрышты табу формуласын жазыңыз.
10. Кеңістікте кезкелген күштер жүйесінің тепе-теңдік шарттары қалай баяндалады?
11. Жазықтықтағы кезкелген күштер тепе-теңдігінің шарттарын айтыңыз және жазыңыз.
§ 5. 6 Жазықтықта кез-келген бағытта бағытталған күштер жүйесіне есептер
Есеп 5. 2
Ауырлығы
Р
1, 8
кн
,
С
нүктесіне түсетін
АВ
уықтың
А
ұшынан өтетін
AD
тросқа
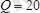 кн.
жүк байланған. Бұл жердегі
кн.
жүк байланған. Бұл жердегі
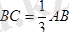 (5. 8 сурет
а
) . Егер
(5. 8 сурет
а
) . Егер
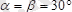 болса, онда
В
топсадағы және
ВА
стержендегі реакция күштері анықталсын.
болса, онда
В
топсадағы және
ВА
стержендегі реакция күштері анықталсын.
Шешуі.
АВ
уықтың тепе-теңдігін қарастырайық.
АВ
уыққа
 және
және
 күштері әсер етеді. . Топса
В
мен
AD
трос байланыстар. Тростың реакция күші
күштері әсер етеді. . Топса
В
мен
AD
трос байланыстар. Тростың реакция күші
 ,
AD
бойлап бағытталған. Топсадағы реакция
,
AD
бойлап бағытталған. Топсадағы реакция
 күшінің шамасы түгілі, қалай бағытталғаны да белгісіз (5. 8 сурет
б
) .
күшінің шамасы түгілі, қалай бағытталғаны да белгісіз (5. 8 сурет
б
) .
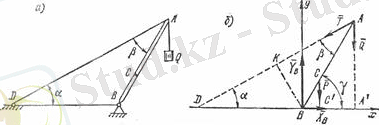
5. 8сурет
 реакция күшін өзара перпендикуляр болған горизонталь
реакция күшін өзара перпендикуляр болған горизонталь
 және вертикаль
және вертикаль
 күштерге жаямыз. Олардың бағыттары
Вх
және
Ву
өстерімен бағыттас болсын. Сонымен,
ВА
уығы
күштерге жаямыз. Олардың бағыттары
Вх
және
Ву
өстерімен бағыттас болсын. Сонымен,
ВА
уығы
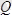 ,
,
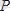 ,
,
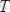 ,
,
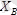 ,
,
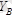 жазық күштер жүйесінің әсерінен өзінің тепе-теңдік күйін сақтайды. Бұлар үшін үш тепе-теңдік теңдеулерін түземіз. Бұл есептегі белгісіздер саны үшеу, яғни:
жазық күштер жүйесінің әсерінен өзінің тепе-теңдік күйін сақтайды. Бұлар үшін үш тепе-теңдік теңдеулерін түземіз. Бұл есептегі белгісіздер саны үшеу, яғни:
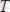 ,
,
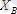 ,
,
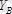 . Демек есеп статикалық анықталатын есептер қатарына жатады. Бұл теңдеулер
. Демек есеп статикалық анықталатын есептер қатарына жатады. Бұл теңдеулер
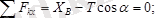
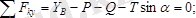
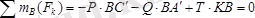
болады.
Суреттен
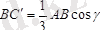 ,
,
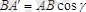 ;
;
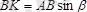 ,
,
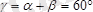 .
.
Бұл шамаларды табылған теңдеулерге апарып қойсақ, онда
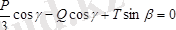 .
.
Демек
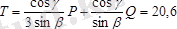 кн.
кн.
Басқа теңдеулерден
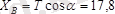 кн.
кн.
және
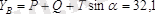 кн.
кн.
анықтаймыз.
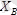 және
және
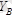 күштердің шамасын анықтай отырып, белгісіз реакция күшін
күштердің шамасын анықтай отырып, белгісіз реакция күшін
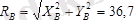 кн.
кн.
табамыз. Бұл күш
Вх
өсімен
 бұрышын құрайды. Олай болса оның косинусы
бұрышын құрайды. Олай болса оның косинусы
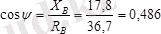 .
.
Демек
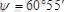 .
.
Уықтың басым күші
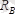 ,
В
топсаның өзіне әсер етіп, оған қарама-қарсы жаққа бағытталады.
,
В
топсаның өзіне әсер етіп, оған қарама-қарсы жаққа бағытталады.
Есеп 5. 3
Салмағы
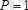 кн,
ұзындығы
2а=2м
біртекті
АВ
сырық, горизонтпен
кн,
ұзындығы
2а=2м
біртекті
АВ
сырық, горизонтпен
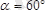 (5. 9 сурет
а
) бұрыш құрап жерге қатты бекітілген. Оған қарқындылығы
(5. 9 сурет
а
) бұрыш құрап жерге қатты бекітілген. Оған қарқындылығы
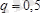 кн/м.
болған тең жайылған күштер әсер етеді. Сырық өз тепе-теңдігін сақтаған кездегі оның жермен бекітілген нүктесіндегі реакция күші анықталсын.
кн/м.
болған тең жайылған күштер әсер етеді. Сырық өз тепе-теңдігін сақтаған кездегі оның жермен бекітілген нүктесіндегі реакция күші анықталсын.
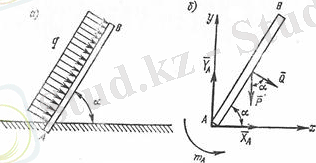
5. 9 сурет
Шешуі.
АВ
сырықтың тепе - теңдігін қарастырайық. Сырыққа, оның салмағы
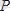 және жайылған күштердің тең әсерлі күші
және жайылған күштердің тең әсерлі күші
 қойылған (5. 9 сурет
б
) .
А
нүктедегі байланыстың сырыққа көрсететін әсерін
қойылған (5. 9 сурет
б
) .
А
нүктедегі байланыстың сырыққа көрсететін әсерін
 және белгісіз жұп күшпен алмастырамыз.
және белгісіз жұп күшпен алмастырамыз.
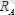 реакция күшін
реакция күшін
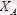 және
және
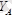 күштерге жаямыз (5. 9 сурет
б
) . Моменті
күштерге жаямыз (5. 9 сурет
б
) . Моменті
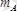 болған жұп күшті сағат тіліне қарама-қарсы бағыттаймыз. Сонымен тепе-теңдікте тұрған сырыққа
болған жұп күшті сағат тіліне қарама-қарсы бағыттаймыз. Сонымен тепе-теңдікте тұрған сырыққа
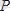 ,
,
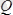 ,
,
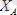 ,
,
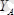 және моменті
және моменті
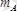 болған жұп күш әсер етеді. Демек сырыққа әсер ететін күштер жүйесі жазық күштер жүйесін құрап, ондағы белгісіздер
болған жұп күш әсер етеді. Демек сырыққа әсер ететін күштер жүйесі жазық күштер жүйесін құрап, ондағы белгісіздер
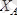 ,
,
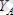 ,
,
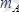 болады, яғни есеп статикалық анықталатын есептер құрамына жатады.
болады, яғни есеп статикалық анықталатын есептер құрамына жатады.
Сырықтың тепе-теңдік теңдеулерін түзейік, яғни
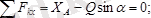
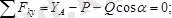
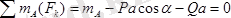
Бұл теңдеулерден
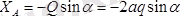 ;
;
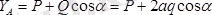 ;
;
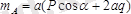 ,
,
келіп шығады. Олардың сан мәндері:
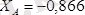 кн;
кн;
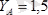 кн;
кн;
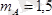
 .
.
Белгісіз
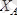 күшіндегі «минус», оның
Ах
өсінің оң бағытына қарама-қарсы бағытталғаны.
күшіндегі «минус», оның
Ах
өсінің оң бағытына қарама-қарсы бағытталғаны.
Сонымен А нүктесіндегі толық реакция күші
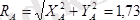 кн,
кн,
ал бағыттаушы косинустар
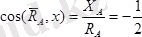 ,
,
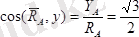 .
.
тең. Демек
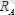 векторы
Ах
пен
векторы
Ах
пен
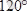 ,
Ау
өсімен
,
Ау
өсімен
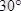 бұрыш құрайды.
бұрыш құрайды.
Есеп 5. 4
Ұзындықтары
2а
екі
АВ
және
ВС
сырықтары (5. 10 сурет
а
) өзара
В
топсасы арқылы бекітілген. Бұл сырықтардың
А
ұшы горизонталь жазықтықпен қатты бекітілген болса,
С
ұшы жылжымалы топсалы тіректе. Сырықтардың горизонталь жазықтықпен құраған бұрыштары
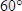 .
ВС
сырықтың ортасына оған перпендикуляр болған
.
ВС
сырықтың ортасына оған перпендикуляр болған
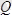 күші әсер етеді. Егер әр-бір сырықтың салмағы
Р
болса, онда
А
және
С
тіректеріндегі және
В
топсадағы реакция күштері неге тең?
күші әсер етеді. Егер әр-бір сырықтың салмағы
Р
болса, онда
А
және
С
тіректеріндегі және
В
топсадағы реакция күштері неге тең?
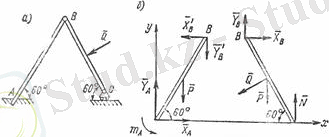
5. 10 сурет
Шешуі.
АВ
және
ВС
сырықтар құрамы өздерінің тепе-теңдігін сақтағаны үшін, олардың әрқайсысы да осындай жағдайда болулары керек. Олай болса
ВС
(5. 10 сурет
б
) . сырығын жеке қарастырсақ, онда оған
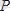 және
және
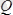 күштері әсер етеді. Бұл жерде
В
топсасы байланыстың қызметін атқара отырып
АВ
сырықтың әсерін
ВС
сырыққа өткізеді. Жылжымалы топсалы тіректің реакция күшін
күштері әсер етеді. Бұл жерде
В
топсасы байланыстың қызметін атқара отырып
АВ
сырықтың әсерін
ВС
сырыққа өткізеді. Жылжымалы топсалы тіректің реакция күшін
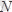 деп белгілейік. Бірақ
В
топсаның шамасы да, бағыты да белгісіз. Оны суретте көрсетілгендей
деп белгілейік. Бірақ
В
топсаның шамасы да, бағыты да белгісіз. Оны суретте көрсетілгендей
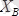 ,
,
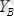 күштерге жіктейміз. Олай болса
ВС
сырығы
күштерге жіктейміз. Олай болса
ВС
сырығы
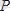 ,
,
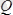 ,
,
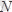 ,
,
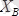 ,
,
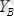 жазық күштер жүйесінің әсерінен өзінің тепе-теңдігін сақтайды. Оның теңдеулері төмендегідей жазылады
жазық күштер жүйесінің әсерінен өзінің тепе-теңдігін сақтайды. Оның теңдеулері төмендегідей жазылады
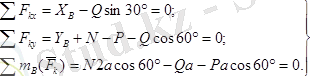
Бұл теңдеулерден
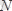 ,
,
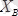 ,
,
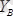 анықталады.
анықталады.
Енді
АВ
сырығының тепе-теңдігін қарастырайық. Оған
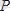 күші әсер етеді. В топсаның
АВ
сырығына көрсететін реакциясын
күші әсер етеді. В топсаның
АВ
сырығына көрсететін реакциясын
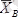 ,
,
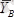 күштеріне жіктейік. Онда Ньютонның үшінші заңы бойынша
күштеріне жіктейік. Онда Ньютонның үшінші заңы бойынша
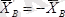 ;
;
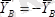 .
.
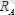 реакция күшін суретте көрсетілгендей
реакция күшін суретте көрсетілгендей
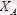 және
және
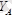 күштерге жіктеп, ал А нүктеде пайда болатын сағат тіліне қарама-қарсы бағытта бағытталған белгісіз жұп күштің моментін
күштерге жіктеп, ал А нүктеде пайда болатын сағат тіліне қарама-қарсы бағытта бағытталған белгісіз жұп күштің моментін
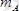 деп белгілейік.
деп белгілейік.
Ол кезде
АВ
сырығы
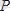 ,
,
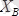 ,
,
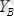 ,
,
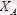 ,
,
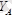 жазық күштер және моменті
жазық күштер және моменті
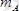 болған жұп күштің әсерінен өзінің тепе-теңдігін сақтап тұр. Оның теңдеулері
болған жұп күштің әсерінен өзінің тепе-теңдігін сақтап тұр. Оның теңдеулері
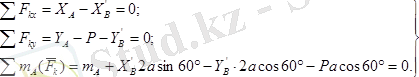
болады.
Бұл теңдеулерді шешсек
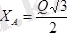 ;
;
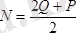 ;
;
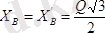 ;
;
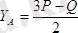 ;
;
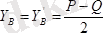 ;
;
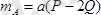 .
.
келіп шығады.
Сонымен
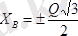 ;
;
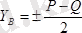 .
.
Есеп 5. 5
Топсалы төрт түйіннен тұратын механизмнің
ОА
бөлігіне моменті
 болған жұп күш әсер етеді. Егер
болған жұп күш әсер етеді. Егер
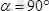 ,
,
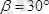 , және
ОА=а,
О
1
В=b
болған кезде, бұл механизм өінің тепе-теңдігін сақтап тұру үшін
О
1
В
стерженге моменті
, және
ОА=а,
О
1
В=b
болған кезде, бұл механизм өінің тепе-теңдігін сақтап тұру үшін
О
1
В
стерженге моменті
 болған қандай жұп күш қойылған болар еді. Стержендердің салмағы және үйкеліс күші есепке алынбасын.
болған қандай жұп күш қойылған болар еді. Стержендердің салмағы және үйкеліс күші есепке алынбасын.
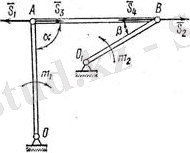
5. 11 сурет.
Шешуі
.
5. 11 суретте көрсетілген механизм өзінің тепе-теңдік күйін сақтағаны үшін, оның әрбір түйіні де осындай қалпын сақтайды.
АВ
стерженнің тепе-теңдік күйін қарастырайық (5. 11 сурет) . Оған
А
және
В
топсалар арқылы
ОА
мен
О
1
В
стержендердің
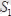 және
және
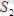 күштері әсер етеді.
АВ
салмақсыз деп алынғандыктан
күштері әсер етеді.
АВ
салмақсыз деп алынғандыктан
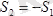 және бұлар
АВ
стержені бойлап бір-біріне қарама-қарсы бағытталған.
және бұлар
АВ
стержені бойлап бір-біріне қарама-қарсы бағытталған.
ОА
және
О
1
В
стержендердің тепе-теңдігін қарастырайық.
ОА
стерженге
АВ
тарапынан
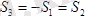 күштер,
О
топсаның реакция күші және моменті
күштер,
О
топсаның реакция күші және моменті
 болған жұп күш әсер етеді. Ал
О
1
В
стерженге
болған жұп күш әсер етеді. Ал
О
1
В
стерженге
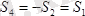 мен
О
1
реакция күштері және моменті
мен
О
1
реакция күштері және моменті
 болған жұп күш әсер етеді.
болған жұп күш әсер етеді.
Біздерді
О
және
О
1
нүктелердегі реакция күштері қызықтырмағаны үшін
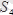 және
және
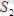 күштерді
О
және
О
1
нүктелерге қатысты алынған моменттердің теңдеулерін түземіз.
күштерді
О
және
О
1
нүктелерге қатысты алынған моменттердің теңдеулерін түземіз.
ОА
үшін
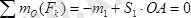 ,
,
О
1
В
үшін
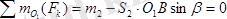
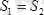 , онда
, онда
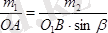 .
.
Немесе
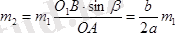 .
.
Есеп 5. 6
Ұзындығы
l
болған
АВ
трубаның
А
нүктесі горизонталь жазықтықта жатып, ал
С
нүктесі вертикаль жазықтыққа тірелген. Бұл жерде
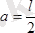 (сурет
а
) . Суреттегі дене өзінің тыныштық күйін сақтағанда,
(сурет
а
) . Суреттегі дене өзінің тыныштық күйін сақтағанда,
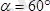 болған кездегі трубамен горизонталь жазықтық арасындағы үйкеліс коэффициентінің ең кіші мәні анықталсын.
болған кездегі трубамен горизонталь жазықтық арасындағы үйкеліс коэффициентінің ең кіші мәні анықталсын.
5. 12 сурет
Шешуі.
Трубаның тепе - теңдігін қарастырайық. Оған оның салмағы
 күші әсер етеді.
А
және
С
(5. 12 сурет
б
) нүктелері байланыстар.
С
нүктедегі реакция күші
күші әсер етеді.
А
және
С
(5. 12 сурет
б
) нүктелері байланыстар.
С
нүктедегі реакция күші
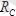 АВ
трубаға, перпендикуляр.
А
нүктедегі реакция күші нормаль
АВ
трубаға, перпендикуляр.
А
нүктедегі реакция күші нормаль
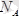 мен горизональ
мен горизональ
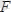 күштерінің құрамынан тұрады. Суретте көрсетілгендей координаталар өстерін қабылдап алып, трубаның тепе-теңдік теңдеулерін түземіз, яғни
күштерінің құрамынан тұрады. Суретте көрсетілгендей координаталар өстерін қабылдап алып, трубаның тепе-теңдік теңдеулерін түземіз, яғни
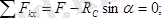
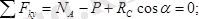
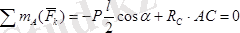
Бұл теңдеулерден
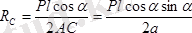 ;
;
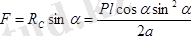 ;
;
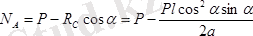
табамыз.
Үйкеліс күші есепке алынған кездегі тепе-теңдік шарты
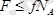
түрде жазылады. Демек
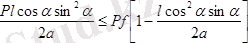 ,
,
немесе
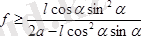 .
.
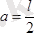 болғаны үшін
болғаны үшін
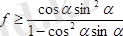 .
.
Бұл өрнектің сан мәндерін еске алсақ, онда
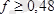 .
.
Есеп 5. 7
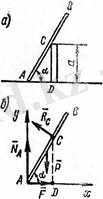
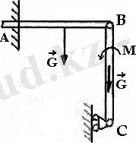
Салмағы G болатын А ұшы қабырғаға кіргізіп бекітілген, В ұшына ВС балка шарнир көмегінде біріктірілген. ВС балканың С ұшы қозғалатын таянышқа бекітілген. ВС балканың салмағы АВ балканың салмағымен бірдей. А, В, С таяныштардағы реакциялар табылсын . ВС балкаға моменті М болатын жұп күш қойылған (5. 13 сурет а) .
АВ=ВС=а
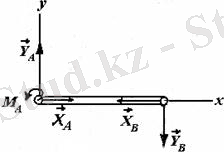
Шешуі. Санау жүйесін (5. 13 сурет, ә, б) дағыдай таңдаймыз. АВ және ВС балкалардың тепе-теңдігін жеке-жеке қарастырамыз. Оларға әсер ететін күштер суретте көрсетілген.
АВ балканың тепе-теңдігінің шарттары төмендегідей болады (5. 13 сурет, ә) :
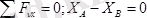 ,
,
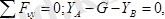 (5. 13)
(5. 13)
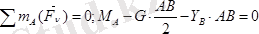
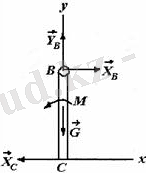
а ә б
5. 13 сурет
ВС балканың тепе-теңдігінің шарттары төмендегідей жазылады (5. 13 сурет, б) :
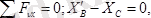
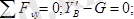 (5. 14)
(5. 14)
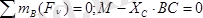
(11. 10), (22. 11) теңдеулерін шешсек:
х А =х В =х С =М/а, у А =2G, у В =G, М А = G а /2.
Есеп 5. 8
Бiр басы қатаң бекiтпедегi қатты денеге екi күш түсiп тұр (1. 14-сурет) . Егер
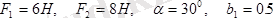
 ,
,
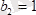
 , болса қатаң бекiтпенiң реакциялары қандай болады?
, болса қатаң бекiтпенiң реакциялары қандай болады?
1. 14-сурет
Шешуi.
Есепте қатаң бекiтпеден дененi босатқаннан соң, денеге әсер етiп тұрған күштер
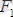 ,
,
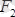 және байланыстың реакциялары
және байланыстың реакциялары
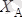 ,
,
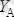 ,
,
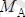
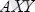 жазықтығында кез келген бағыттағы күштер жүйесiн құрады. (1. 8. 2) өрнек бойынша бұл күштер жүйесiнiң тепе-теңдiк теңдеулерi мына түрде жазылады:
жазықтығында кез келген бағыттағы күштер жүйесiн құрады. (1. 8. 2) өрнек бойынша бұл күштер жүйесiнiң тепе-теңдiк теңдеулерi мына түрде жазылады:
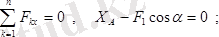
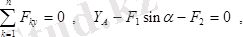
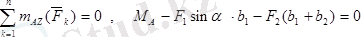
Бұл теңдеулерден:
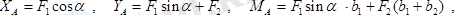
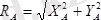
немесе
X
A
=5. 196H, Y
A
=11. 00H, M
A
=13. 5H, R
A
=12. 16H.
Есеп 5. 9
Екi ұшы екi тiректен бiрдей ұзындыққа асып тұрған балкаға моментi
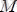 -ге тең қос күш,
-ге тең қос күш,
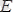 нүктесiне
нүктесiне
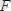 күшi, ұшбұрыш заңдылығымен және бiр қалыпты жайылып түскен күштер әсер етiп тұр (1. 15, а-сурет) .
күшi, ұшбұрыш заңдылығымен және бiр қалыпты жайылып түскен күштер әсер етiп тұр (1. 15, а-сурет) .
1. 15 - сурет
Үшбұрыш заңдылығымен жайылып түскен күштердiң қарқындылығы 0-ден q
max
=6H/м дейiн өзгергенде, қос күштiң моментi М=3Нм, күштiң шамасы F=11Hбiр қалыпты жайылып түскен күштердiң қарқындылығы q
0
=2H/м, a=30
0
,
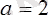 м болған жағдайда байланыстардың реакциялары қандай болады?
м болған жағдайда байланыстардың реакциялары қандай болады?
Шешуi.
Алдыменен жайылып түскен күштердiң тең әсер етушi күштерiн анықтайық. Әр ұзындығы DX
k
учаскесiне
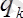 DX
k
кѕшi түседi, сондықтан бұл күштердiң тең әсер етушi күшi
DX
k
кѕшi түседi, сондықтан бұл күштердiң тең әсер етушi күшi
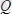 мына интегралдан табылады
мына интегралдан табылады
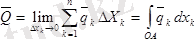
Табандары Х
к
және
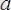 ѕшбЅрыштардан (1. 15, а-сурет) :
ѕшбЅрыштардан (1. 15, а-сурет) :
 өйткенi ол үшбұрыштар ұқсас үшбұрыштар. Табылған
өйткенi ол үшбұрыштар ұқсас үшбұрыштар. Табылған
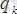 мәнiн жоғарыдағы интегралға енгiзсек, онда
мәнiн жоғарыдағы интегралға енгiзсек, онда
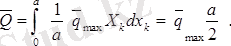
ендi
 нѕктесiнен
нѕктесiнен
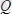 қандай аралықта өтетiнiн бiлу үшiн Вариньон теоремасын (лекциядан қара) қолданайық, сонда
қандай аралықта өтетiнiн бiлу үшiн Вариньон теоремасын (лекциядан қара) қолданайық, сонда
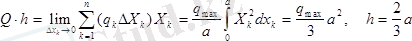
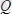 -дың медианалар қиылысқан нүктесiнен, яғни үшбұрыштың ауырлық центрiнен өтетiнiн анықтадық.
-дың медианалар қиылысқан нүктесiнен, яғни үшбұрыштың ауырлық центрiнен өтетiнiн анықтадық.
Бiр қалыпты жайылған күштердiң тең әсер етушi күшi
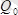 жайылу учаскесiнiң қақ ортасынан төмен қарай бағытталады.
жайылу учаскесiнiң қақ ортасынан төмен қарай бағытталады.
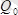 -дың шамасы жайылу учаскесiнiң ұзындығымен қарқындылықтың көбейтiндiсiне тең:
-дың шамасы жайылу учаскесiнiң ұзындығымен қарқындылықтың көбейтiндiсiне тең:
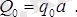
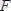 күшiнен момент алғанда иiндерi жеңiл анықталу үшiн күштi былай жiктейiк
күшiнен момент алғанда иiндерi жеңiл анықталу үшiн күштi былай жiктейiк

Ендi балкаға әсер етiп тұрған күштердiң барлығын ескере отырып ол күштердiң аналитикалық тепе-теңдiк теңдеулерiн жазайық. 1. 15,
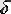 - суретiндегi күштер жазықтықта кез келген бағыттағы күштер жүйесiн құрап тұр, сондықтан
- суретiндегi күштер жазықтықта кез келген бағыттағы күштер жүйесiн құрап тұр, сондықтан
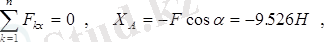
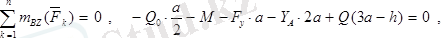
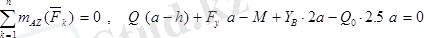
Бұл теңдеулерден:
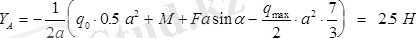 .
.
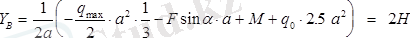
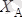 мен
мен
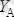 бiр-бiрiне перпендикуляр екенiн пайдалансақ, онда:
бiр-бiрiне перпендикуляр екенiн пайдалансақ, онда:
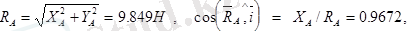
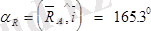
Есеп 5. 9
Екi денеден құрасқан денелер жүйесiне
 ,
,
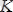 нүктелерiне F
1
=5H, F
2
=6H күштерi, ЕВ учаскесiне қарқындылығы q=1. 75 H/м тең бiр қалыпты жайылып түскен күштер түсiп тұр (1. 16,
нүктелерiне F
1
=5H, F
2
=6H күштерi, ЕВ учаскесiне қарқындылығы q=1. 75 H/м тең бiр қалыпты жайылып түскен күштер түсiп тұр (1. 16,
 -сурет) . Жайылу учаскесiнiң ұзындығы
-сурет) . Жайылу учаскесiнiң ұзындығы
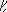 =4 м, күштердiң көкжиекпен жасаған бұрыштары a
1
=1. 0472, a
2
=0. 7854
рад
болған жағдайда сыртқы және iшкi байланыстардың реакцияларын анықтаңыздар.
=4 м, күштердiң көкжиекпен жасаған бұрыштары a
1
=1. 0472, a
2
=0. 7854
рад
болған жағдайда сыртқы және iшкi байланыстардың реакцияларын анықтаңыздар.
Шешуi.
 топсасынан денелер жѕйесiн екi денеге бөлiп алайық.
топсасынан денелер жѕйесiн екi денеге бөлiп алайық.
 топсасының реакциясын әр денеде
топсасының реакциясын әр денеде
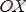 ,
,
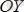 өстерiне жiктеп шамалары мен бағыттарын былай етiп аламыз
өстерiне жiктеп шамалары мен бағыттарын былай етiп аламыз
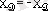 ,
,
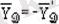 . Бұл есепте
. Бұл есепте
 iшкi, ал
iшкi, ал
 сыртқы байланыстарға жатады.
сыртқы байланыстарға жатады.
 топсасының реакцияларынан басқа әр денеге тиiстi күш-тердi бағыттағаннан соң әр денеге жазық тықта кез келген бағыттағы күштер жүйесi әсер етедi (1. 16,
топсасының реакцияларынан басқа әр денеге тиiстi күш-тердi бағыттағаннан соң әр денеге жазық тықта кез келген бағыттағы күштер жүйесi әсер етедi (1. 16,
 ,
,
 -суреттер) .
-суреттер) .
1. 16-сурет
 денесiне түсiп тұрған күштердiң тепе-теңдiк теңдеулерiн жазайық:
денесiне түсiп тұрған күштердiң тепе-теңдiк теңдеулерiн жазайық:
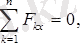 X
Д
+ F
2
cos a
2
=0,
X
Д
+ F
2
cos a
2
=0,
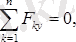 Y
Д
+Y
C
-F
2
sin a
2
=0,
Y
Д
+Y
C
-F
2
sin a
2
=0,
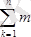 ДZ
ДZ
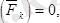 Y
C
l
-F
2
sin a
2
.
2
l
=0.
Y
C
l
-F
2
sin a
2
.
2
l
=0.
Бұл теңдеулерден:
X Д = - F 2 cos a 2 = - 4. 2426H, Y C =2 F 2 sin a 2 = 8. 4853H, Y Д = - 4. 2426H.
Ендi Ад денесiне түсiп тұрған күштердiң тепе-теңдiк теңдеулерiн жазайық (1. 16,
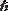 -сурет) :
-сурет) :
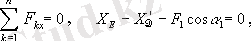
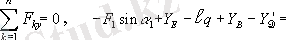
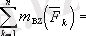
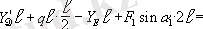
Бұл теңдеулерде штрих қойылған мүшелердiң мәнiн ескерсек, қалған белгiсiздердi анықтауға болады
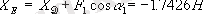
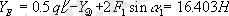
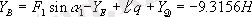
Денелер жүйесiне сыртқы байланыстардың реакциялары мен барлық күштердi түсiрiп жоғарыда анықталған реакцияларды тексерейiк(1. 16,
 -сурет) :
-сурет) :
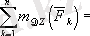
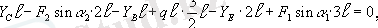
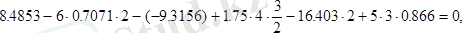
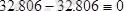
Анықталған реакцияларды
 нѕктесiне қатысты барлық күштер мен реакциялардың моменттерiнiң қосындысына енгiзгенде, ол теңдеу қанағаттанды, сондықтан табылған реакциялардың мәндерi дұрыс екенiне сенуге болады.
нѕктесiне қатысты барлық күштер мен реакциялардың моменттерiнiң қосындысына енгiзгенде, ол теңдеу қанағаттанды, сондықтан табылған реакциялардың мәндерi дұрыс екенiне сенуге болады.
 мәндерiнiң алдындағы керi таңба бұл реакциялардың бағыттары 1. 15,
мәндерiнiң алдындағы керi таңба бұл реакциялардың бағыттары 1. 15,
 -суреттердегi бағыттарға қарама-қарсы екенiн бiлдiредi.
-суреттердегi бағыттарға қарама-қарсы екенiн бiлдiредi.
§ 5. 7 Кеңістіктегі кез-келген бағытта бағытталған күштер жүйесіне арналған есептер
Есеп 5. 10
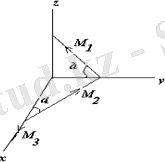
5. 17 суретте көрсетілген жұп моменттерінің тең әсерлі моментінің модулі табылсын.
М
1
=М
2
=1Нм, М
3
=0, 707Нм,
 =45
0
.
=45
0
.
 Шешуі.
5. 17 суретте көрсетілген жұп моменттері кеңістікте орналасқан. Кеңістіктегі жұп моменттерінің геометриялық қосындысы олардың бас моментінен тұратыны бізге белгілі.
Шешуі.
5. 17 суретте көрсетілген жұп моменттері кеңістікте орналасқан. Кеңістіктегі жұп моменттерінің геометриялық қосындысы олардың бас моментінен тұратыны бізге белгілі.
Жұп моменттерін Ох, Оу, Оz өстеріне проекциялаймыз:
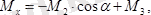
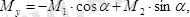
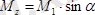
5. 17 сурет
Сан мәндерін қойсақ :
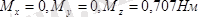
Нәтижеде
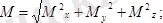 M = 0, 707Нм
M = 0, 707Нм
келіп шығады.
Есеп 5. 11
Салмағы
G
=1, 6
кН
болатын барабан өсіне шынжыр оралған, оның керілуі
Т
=20
см
(5. 18 сурет, а) . барабан
S
шестерняға қойылған
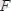 күш әсерінде тепе-теңдікте тұрады.
күш әсерінде тепе-теңдікте тұрады.
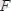 және
және
 Оу осіне параллель
, r
2
=40
см
. Шестерня центрі
А
подпятниктен
AS
=10
см
қашықтықта орналасқан.
АВ
=120
см
,
SD
=40
см
.
А
подпятник,
В
подшипник реакциялары және
Оу осіне параллель
, r
2
=40
см
. Шестерня центрі
А
подпятниктен
AS
=10
см
қашықтықта орналасқан.
АВ
=120
см
,
SD
=40
см
.
А
подпятник,
В
подшипник реакциялары және
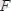 күш мөлшері табылсын.
күш мөлшері табылсын.
Шешуі. (5. 18 сурет, а) дегі барабан тепе-теңдігін тексереміз. А подпятник, В подшипник әсерлесін сәйкес түрде
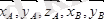 реакция күштерімен ауыстырамыз. Онда барабан
реакция күштерімен ауыстырамыз. Онда барабан
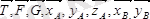 күштер әсерінде тепе-теңдікте болады. Бұл күштер кеңістіктегі кезкелген күштер жүйесінен тұрады.
күштер әсерінде тепе-теңдікте болады. Бұл күштер кеңістіктегі кезкелген күштер жүйесінен тұрады.
Демек, тепе-теңдік теңдеулері төмендегідей болады:
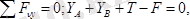
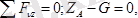
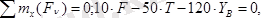
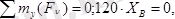
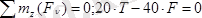
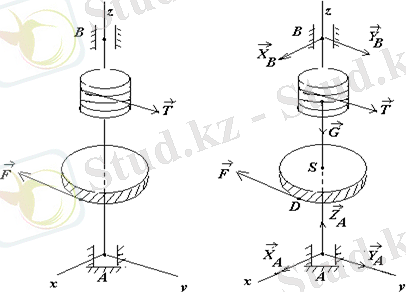
а ә
5. 18 сурет
Сан мәндерін қойсақ:
х А =0, , у А =-2, 5кН, z A =1, 6кН, х В =0, у В =-7, 5кН, F=10кН.
Мұндағы (-) таңба у А , у В -лардың ақиқат бағыты (5. 18 сурет, а) - дағыға кері болады.
Есеп 5. 12
Салмағы
Р
болған тікбұрышты
ABCD
плита
А
топсасы,
CN
,
CK
стержендер және
BS
тросы (5. 19 сурет
а
) арқылы горизонталь бекітілген. Стержендердің салмағы есепке алынбаған кездегі, барлық байланыстар топсадан тұрады деп және
В
нүктесіне салмағы
Q
болған
М
жүгі ілінген болса
А
нүктесіндегі реакция күші, стержендердегі және тростағы белгісіз ішкі күштер анықталсын.
A, B, C, D, L, E, F, K
тікбұрыштарының ұштарына орналасқан. Олардың қабырғалары
CD
=3
а
;
CB
=4
а
;
CE
=5
а
тең. Тростың бекітілген
S
нүктесі
FD
сызығының жалғасында жатыр және
 SBD
=45
0
.
SBD
=45
0
.
Шешуі.
Плитаның тепе-теңдігін қарастырайық. Оған белгілі
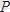 және
және
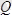 күштері әсер етеді.
А
нүктесі,
CN
,
CK
стержендер және
BS
күштері әсер етеді.
А
нүктесі,
CN
,
CK
стержендер және
BS
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz