Stud.kz

Сызықтық программалаудың негізгі есебі


Пән: Информатика, Программалау, Мәліметтер қоры
Жұмыс түрі:  Материал
Тегін:  Антиплагиат
Көлемі: 57 бет
Таңдаулыға:   

КІРІСПЕ

Қазіргі заманғы қоғамның дамуын мынадай деңгейлермен сипаттауға болады: техникалық білімдерінің жоғарылауымен, өндіріс орындары талаптарының өсуімен, қоғамдық еңбек дамуымен, жоспарлау әдістеріне, шаруашылық басқаруға деген жоғарғы талап қоюумен. Бұл жағдайларда басшыларға қоғамның экономикалық өміріне ғылыми тәсілдер қолдану халық шаруашылығының қарқынды дамуына ықпал етеді.

Экономиканың әріқарай дамуының қажетті шарттарының бірі және бірегейлері сандық анализдің нақты әдістерінің қолданылуы және де математиканың кеңінен қолданылуы ықпал етеді.

Қазіргі таңда математиканың ең жоғарғы жетістіктерімен, заманауи есептік техниканың жетістіктері, экономикалық зерттеулермен жоспарлауларда кеңінен қолданылуда. Бұл мақсатта қолданылып жұрген математикалық жетістіктер: математикалық программалау, ойын теориясы, жалпыға қызмет ету теориясы секілді көптеген математикалық әдістер. Қазіргі таңда көптеген экономикалық есептер және экономикалық шешімдерді математикалық әдістерді қолдануда. Айтарлықтай табысқа жеткен әдістерінің бірі оптималды жоспарлау. Ал ол өз кезегінде математикалық программалаудың негізі болуда. Болашақ бағдарламашылар үшін қолданылған математиканың ең маңызды саласының бірі - математикалық бағдарламалау; Ол экстремальді есептерді зерттеуге және оларды шешу әдістеріне арналған. Бұл пәнді оқу студентке қарапайым экономикалық есептердің математикалық модельдерін құрастыруда алғашқы қадам жасауға, математикалық қойылыммен шешу әдістерін үйренуге мүмкіншілік береді.

Экстремальды экономикалық есеп шешімдерін үш кезеңге бөлуге болады:

  1. Экономикалық математиканың моделін құру.
  2. Оптималды шешімдердің біреуін математикалық әдіспен табу.
  3. Практикалық көзқарас және халық шаруашылық.

Экономиканың математикалық моделін құру үшін алдымен экономикалық процестің математикалық моделін солай құру керек, онда оның шынайылығы көрініп тұратындай болуы керек.

Математикалық программалаудың құрамдас бөліктері үшке бөлінеді. Олар: Сызықтық, сызықтық емес және динамикалық программалау.

Алғашқы рет сызықтық программалаудың есебін совет экономисті А. Н. Толстой 1930 жылы қойды. Ал 1931 жылы венгерлік математик Б. Эгервари сызықтық программалаудың математикалық түрде қойылуын қарастырып, оған «таңдау кедергісі» деп аталып, венгерлік шешім деген атқа ие болды. Жүйелі түрде зерттеулер нәтижесінде сызықтық программалаудың есебін, жалпы әдісін және шешімін табуды совет ғалымы Л. В. Канторовичтің (1932) жұмыстарында берілген жалпы шешімдерін табу әдісін ұсынды. Ол М. К. Гавуринмен бірлесе отырып потенциал әдісін ойлап табуды және оны транпорттық есептерді шешуде қолданды.

Сызықтық программалаудың әдістерін жақын шет елдегі ғалымдар да зерттеді. Дәлірек айтар болсақ, американдық ғалым 1941 жылы Хичкок транспорттық есепті қойды. Сызықтық программалауды шешудің негізгі әдісі ретінде - симплекс әдісі болып жарияланды. Ол 1949 жылы Данциг жариялады. Одан әрі қарай да көптеген ғалымдар өз еңбектерін сызықтық және сызықтық емес программалау әдістерін дамытты.

1 СЫЗЫҚТЫҚ ПРОГРАММАЛАУДЫҢ НЕГІЗГІ ЕСЕБІ

1. 1 ЖӘЙ ЭКОНОМИКАЛЫҚ ЕСЕПТЕР

Шикізатты қолдану есебі

Екі түрлі П 1 П_{1} және П 2 П_{2} өнімдерін дайындау үшін төрт түрлі шикізат қажет деп болжайық: S 1 , S 2 , S 3 , S 4 S_{1\ }, \ \ S_{2}, \ \ S_{3}{, \ \ S}_{4} . Әр шикізат қоры шектеулі, яғни b 1 , b 2 , b 3 , b 4 b_{1}, \ b_{2}, b_{3}, b_{4} шартты бірліктері. Шикізат қорлары, өнімнің әр данасы үшін жұмсалатын шикізат көлемі белгілі болсын. (1-кесте)

Кесте 1

Шикізат түрлері
Шикізат қоры
Өнім түрлері
П 1 П_{1}
П 2 П_{2}
Шикізат түрлері:

S 1 S_{1}

S 2 S_{2}

S 3 S_{3}

S 4 S_{4}

Шикізат қоры:

b 1 b_{1}

b 2 b_{2}

b 3 b_{3}

b 4 b_{4}

Өнім түрлері:

a 11 a_{11}

a 21 a_{21}

a 31 a_{31}

a 41 a_{41}

a 12 a_{12}

a 22 a_{22}

a 32 a_{32}

a 42 a_{42}

Шикізат түрлері: Кіріс
Шикізат қоры: C 1 C_{1}
Өнім түрлері: C 2 C_{2}

мұнда a i j ( i = 1 , . . , 4 ; j = 1 , 2 ) a_{ij}(i = 1, . ., 4; j = 1, 2) П j П_{j} түріндегі өнімді өндіру үшін S i S_{i} түріндегі шикізат көлемі кестедегі соңғы қатарда әрбір өнімнен түскен өндірістің пайдасы.

П 1 ж ә н е П 2 П_{1}\ және\ П_{2} өнім шығару үшін максимальды пайда түсім беретін өнім өндіру жобасын құру керек болсын. Математикалық түрде берілуін келесі сандық мысалда көреміз (2 - кесте) .

Кесте 2

Шикізат түрлері
Шикізат қоры
Өнім түрлері
П 1 П_{1}
П 2 П_{2}
Шикізат түрлері:

S 1 S_{1}

S 2 S_{2}

S 3 S_{3}

S 4 S_{4}

Шикізат қоры:

19

13

15

18

Өнім түрлері:

2

2

0

3

3

1

3

0

Шикізат түрлері: Кіріс
Шикізат қоры: 7
Өнім түрлері: 5

Айталық П 1 П_{1} -деп x 1 x_{1} , П 2 П_{2} -деп x 2 x_{2} өнімдер дайындалсын. Ол үшін S 1 S_{1} -деп 2 x 1 x_{1} + 3 x 2 x_{2} бірлік шикізат алу талап етілсін (2-кесте) . Сонымен S 1 S_{1\ \ } - де барлығы 19 бірлік шикізат мөлшері болса, онда ол

2 x 1 x_{1} + 3 x 2 x_{2} ≤ 19 \leq 19

теңсіздігін орындау керек.

Теңсіздік S 1 S_{1\ \ } - дегі шикізат қорлары толықтай пайдаланбай өндіріс максимальды табысқа жетуі қарастырылған.

Ал қалған шикізаттың түрлері келесі теңсіздікпен берілген

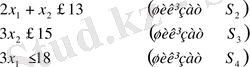
Осындай шарттармен өндіріске түскен табыс

F = 7 x 1 + 5 x 2 F = {7x}_{1} + {5x}_{2\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }

құрайды.

Сонымен математикалық есеп былай тұжырымдалады

(1. 1. 1)

жүйесі берілген, төрт сызықтық теңсіздіктен сызықтық форма

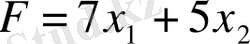(1. 1. 2)

түрінде болады.

Теріс емес шешімдерден (1. 1. 1) теңсіздіктер жүйесінен шешімді F формасы ең үлкен мән қабылдайтындай етіп таңдауға болады.

Құрылғылардың қуаттылығын пайдалану есебі.

Өнеркәсіп өндірісте уақыт және наменклатура бойынша жоспар құрған. П 1 П_{1} -түрдегі N 1 N_{1} - өнімді және П 2 П_{2} - дегі N 2 N_{2} - өнімді T уақытта шығаруы керек болсын. Әрбір түрлі өнімді әртүрліқуаттылығына қарай А және В екі машинамен өндіруі мүмкін. Бұл қуаттылықтар 3- кестеде көрсетілген. Мұнда a 1 a_{1} - А машинамен бірлік уақытта өндірілген П 1 П_{1} түрдегі өнім мөлшері. Ал қалғандарының да берілгендері кестеде көрсетілген.

Кесте 3 Кесте 4 Кесте 5

П 1 П_{1}
П 2 П_{2}
П 1 П_{1}
П 2 П_{2}
П 1 П_{1}
П 2 П_{2}
А
a 1 a_{1}
a 2 a_{2}
A
α 1 \alpha_{1}
α 2 \alpha_{2}
A
x 1 x_{1}
x 2 x_{2}
В
b 1 b_{1}
b 2 b_{2}
B
β 1 \beta_{1}
β 2 \beta_{2}
B
x 3 x_{3}
x 4 x_{4}

Берілген машинада өнімдердің түрлеріне қарай шығындарда әр түрлі болып табылады және 4 - кестеде көрсетілген.

Бұл кестеде α 1 \alpha_{1} мен- П 1 П_{1} түрдегі дайындалған өнімнің А машинасындағы жұмыс уақытының бірлік бағасын өрнектейді. Ал қалған α 2 , β 1 , β 2 \alpha_{2}, \beta_{1}, \beta_{2} шамаларыда өзгелерге ұқсас.

Машинаның жұмыс жасауының оптимальды жоспарын, атап айтсақ әрбір А және В машиналары П 1 П_{1} және П 2 П_{2} түрдегі өнімдерді қанша уақытта дайындағанда, өндірістегі өнімдердің құны минималь болатындай етіп құру керек.

Қойылған есептің математикалық тұжырымдамасын жасайық. Өнімдерді өндіру үшін машинаның жұмыс уақытына (5 кестеде) көрсетілгендей белгілеулер енгіземіз. Мұнда, мысалыға x 1 x_{1} - П 1 П_{1\ } түрдегі өнімді А машинасында дайындау уақытын көрсетеді. Сондай-aқ x 2 , x 3 , x 4 x_{2}, x_{3}, x_{4} осындай болады.

Қаншалықты А А және В В машиналары бір уақытта жұмыс жасаса, уақыт бойынша жоспарды орындау келесі теңсіздіктермен қамтамасыз етеді.

x 1 + x 2 ≤ T , x_{1} + x_{2} \leq T,

x 3 + x 4 ≤ T . x_{3} + x_{4} \leq T.

Бұл теңсіздіктің сол жағы А А және В В машиналарына сәйкес жалпы жұмыс уақытын білдіреді.

x 1 x_{1} уақыт бірлігінде П П өнімін А А машинасында дайындайды. Сонымен А А машинасында П 1 П_{1\ } өнімді В В машинасында b 1 x 3 b_{1}x_{3} бірлікте дайындайды. Сондықтан жоспарды нөмір бойынша қамтамасыз ету үшін келесі теңдік орындалуы тиіс.

a 1 x 1 + b 1 x 3 = N 1 . a_{1}x_{1} + b_{1}x_{3} = N_{1}.

Дәл осылай П 2 П_{2} өнімді шығару жоспарын қамтамасыз ету үшін келесі теңдікті қанағаттандыруы тиіс.

a 2 x 2 + b 2 x 4 = N 2 . a_{2}x_{2} + b_{2}x_{4} = N_{2}.

Бұдан әрі осы шарттардан барлық өнімдердің жалпы бағасы

F = a 1 x 1 + a 2 x 2 + β 1 x 3 + β 2 x 4 . F = a_{1}x_{1} + a_{2}x_{2} + \beta_{1}x_{3} + \beta_{2}x_{4}.

құрайды.

Қорытындысында келесі математикалық есепке келеміз.

x 1 + x 2 ≤ T , x 3 + x 4 ≤ T , a 1 x 1 + b 1 x 3 ≥ N 1 , a 2 x 2 + b 2 x 4 ≥ N 2 . } \left. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array}{r} x_{1} + x_{2} \leq T, \\ x_{3} + x_{4} \leq T, \\ a_{1}x_{1} + b_{1}x_{3} \geq N_{1}, \\ a_{2}x_{2} + b_{2}x_{4}{\geq N}_{2}. \end{array} \right\} (1. 1. 3)

екі сызықтық теңдеумен екі сызықтық теңсіздіктерден сызықтық форма беріледі

F = α 1 x 1 + α 2 x 2 + β 1 x 3 + β 2 x 4 . \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ F = \alpha_{1}x_{1} + \alpha_{2}x_{2} + \beta_{1}x_{3} + \beta_{2}x_{4}. (1. 1. 4)

(1. 1. 3) жүйеден барлық теріс емес шешімдердің арасынан F F форма қай кезде ең

аз мәнді қабылдайтындығын табу керек.

Қойылған есептен бір ең маңызды нұсқасын белгілейміз.

А А және В В машиналары барлық T T уақытта жоспар бойынша жүргізуін талап етеміз. Сонда

x 1 + x 2 ≤ T , x_{1} + x_{2} \leq T,

x 3 + x 4 ≤ T x_{3} + x_{4} \leq T

Теңсіздігі теңдікке өтеді. Сол кезде соңғы (1. 1. 3) жүйедегі екі теңдік теңсіздікке өтеді.

a 1 x 1 + b 1 x 3 ≥ N 1 , a_{1}x_{1} + b_{1}x_{3} \geq N_{1},

a 2 x 2 + b 2 x 4 ≥ N 2 . a_{2}x_{2} + b_{2}x_{4}{\geq N}_{2}.

Сонда T T уақыттағы машиналар жұмыс тек қана жоспар бойынша асыра орындайды. Сондықтан минимизациялау талабы бойынша нөмір бойынша артық орындауды теріске шығара алмайды.

Транспорт есебі

A 1 ж ә н е A 2 A_{1\ \ }және\ A_{2\ \ } екі станциядан a 1 ж ә н е a 2 a_{1\ \ }және\ a_{2\ \ } сәйкес біртекті бірлік жүкті жіберу керек. Бұл жүктерді b 1 , b 2 , b 3 b_{1}, b_{2}, \ b_{3} мөлшерінде B 1 , B 2 , B 3 B_{1}, B_{2}, \ B_{3} пунктіне тасымалдау керек. A i A_{i\ } пунктінен B j B_{j\ } пунктіне жүкті тасымалдау құны C i j \ \ C_{ij} белгілі. Берілген мәліметтер 6-шы кестеде көрсетілген.

Кесте 6

Қабылдау

пункті

Жіберу

пункті

Тағайындау пункті
Жүк қорлары
B 1 B_{1}
B 2 B_{2}
B 3 B_{3}
ҚабылдаупунктіЖіберупункті:

A 1 A_{1}

A 2 A_{2}

Тағайындау пункті:

C 11 C_{11}

C 21 C_{21}

Жүк қорлары:

C 12 C_{12}

C 22 C_{22}

C 13 C_{13}

C 23 C_{23}

a 1 a_{1}

a 2 a_{2}

ҚабылдаупунктіЖіберупункті:

Жүкке

қажеттілік

Тағайындау пункті: b 1 b_{1}
Жүк қорлары: b 2 b_{2}
b 3 b_{3}
∑ a i = ∑ b j \sum_{}^{}{a_{i} = \sum_{}^{}b_{j}}

Станциялардағы жүкті тасымалдаудың жалпы қоры осы жүкті жеткізудегі сұраныстың қосындысына тең болады. Шындығында

a 1 + a 3 = b 1 + b 2 + b 3 . a_{1} + a_{3} = b_{1} + b_{2} + b_{3}. (1. 1. 5)

Тасымалдау бағасы ең аз болатын жоспарда құруымыз керек.

A i A_{i\ } пунктінен B i B_{i\ }\ пунктіне жіберілетін жүктің санын x i j x_{ij} деп белгілейміз. Сонда жүктің саны A 1 ж ә н е A 2 A_{1\ \ }және\ A_{2\ \ } пункттерінен B 1 B_{1} пунктеріне жеткізу жоспарланған,

x 11 + x 21 . x_{11} + x_{21}.

деп қорылады.

Ал бірақ B 1 B_{1} пункттегі жүктің қажеттілігі b 1 b_{1} -ге тең болса, онда

x 11 + x 21 = b 1 . x_{11} + x_{21} = b_{1}.

орындалады.

Дәл осындай талқылаулардан келесі теңдік бере келеміз.

x 12 + x 22 = b 2 , x_{12} + x_{22} = b_{2},

x 13 + x 23 = b 3 . x_{13} + x_{23} = b_{3}.

Басқаша айтқанда А станциясынан жіберілген жүктің жалпы мөлшері

x 11 + x 12 + x 13 , x_{11} + x_{12} + x_{13},

қосындысымен өрнектеледі, бұдан байқағанымыз A 1 A_{1\ \ } пунктінен пайдалану пункттеріне жіберілген жүктердің қосындысы

x 11 + x 12 + x 13 = a 1 . x_{11} + x_{12} + x_{13} = a_{1}.

сондай-ақ

x 21 + x 22 + x 23 = a 2 . x_{21} + x_{22} + x_{23} = a_{2}.

Алынған қатынастарды есте сақтап, барлық шамаларды кестеге енгіземіз. Сонда i-нші қатарда орналасқан барлық x i j x_{ij} қосындысын оңай тексеруге болады. A i A_{i\ } пунктіндегі тасымалдау a i a_{i} қорына тең. j-ші қатарларға x i j x_{ij} қосындысы b j b_{j} -ге тасымалдау B j {\ B}_{j} -тең. Есептің шарттарынан тасымалдаудың барлық F бағасы

F = c 11 x 11 + c 12 x 12 + c 13 x 13 + c 21 x 21 + c 22 x 22 + c 23 x 23 = = ∑ i = 1 2 ∑ j = 1 3 c i j x i j = ∑ i , j c i j x i j . F = c_{11}x_{11} + c_{12}x_{12} + c_{13}x_{13} + c_{21}x_{21} + c_{22}x_{22} + c_{23}x_{23} = = \sum_{i = 1}^{2}{\sum_{j = 1}^{3}{c_{ij}x_{ij} = \sum_{i, j}^{}{c_{ij}x_{ij}. }}}

тең.

Кесте 7

Белгіленген

орны

Жіберу

Орны

B 1 B_{1}
B 2 B_{2}
B 3 B_{3}

Қосымша

Қорлар

7 кесте жалғасы

A 1 A_{1}

A 2 A_{2}

x 11 x_{11}

x 21 x_{21}

x 12 x_{12}

x 22 x_{22}

x 13 x_{13}

x 23 x_{23}

a 1 a_{1}

a 2 a_{2}

A1A_{1}A2A_{2}: Қажеттілер
x11x_{11}x21x_{21}: b 1 b_{1}
x12x_{12}x22x_{22}: b 2 b_{2}
x13x_{13}x23x_{23}: b 3 b_{3}
a1a_{1}a2a_{2}:

Сонымен транспорт есебінің математикалық тұжырымдамасы мынадай

x 11 + x 21 = b 1 , x 12 + x 22 = b 2 , x 13 + x 23 = b 3 , x 11 + x 12 + x 13 = a 1 , x 21 + x 22 + x 23 = a 2 . } \left. \ \ \begin{array}{r} x_{11}{+ x}_{21} = b_{1}, \\ x_{12}{+ x}_{22} = b_{2}, \\ x_{13}{+ x}_{23} = b_{3}, \\ x_{11}{+ x}_{12}{+ x}_{13} = a_{1}, \\ x_{21}{+ x}_{22}{+ x}_{23} = a_{2}. \end{array} \right\} (1. 1. 6)

Алты айнымалылар арқылы бес сызықтың алгебралық теңдеулерден сызықтық форма

F = ∑ i , j c i j x i j . ( 1. 1 . 7 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ F = \sum_{i, j}^{}{c_{ij}x_{ij}. }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1. 1. 7)

(1. 1. 6) теңдеулер жүйесінен x i j x_{ij} шешімінің барлық теріс емес шешімдерінін F F формасы минимал, яғни ең кіші мәнге ие болатын шешімін таңдап аламыз.

Сонымен, транспорт есебін шешу барысында ең маңызды қатынасты ескерсек, осы шарттардан

∑ i a i = ∑ j b j ( 1. 1 . 5 ′ ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum_{i}^{}{a_{i} = \sum_{j}^{}b_{j}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1. 1. 5')

шығады.

Алайда кей жағдайда ( 1. 1 . 5 ′ ) {(1. 1. 5}') шарты орындалмайтын да есептердің қойылуы мүмкін.

Азықтандыру есебі

Адам өз өмірінде денсаулығын сақтау және жұмысқа деген құлшынысын арттыру үшін бір күнде кейбір құнарлы заттарды пайдалануы тиіс, мысалға белоктар, майлар, көмірқышқылдар, су және дәрумендер. Бұл қоспалардың қорлары әртүрлі түрдегі π i ( i = 1 , 2 , … ) \pi_{i}(i = 1, 2, \ldots) тағамдарда әртүрлі. Қарапайым түрде екі түрлі тағамның түрін алып 8 кестедегі түрде берейік, мысалыға a 11 a_{11} саны π i \pi_{i} түрдегі тағамдағы майлардың қорын береді, ал қалған a i j a_{ij} сандары осы тектес алынады.

Кесте 8

Құнарлы өнімдер
Қалыпты
Тағам түрлері
π 1 \pi_{1}
π 2 \pi_{2}
Құнарлы өнімдер:

B 1 − м а й л а р {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ B}_{1} - майлар

B 2 − н ә р у ы з д а р {\ B}_{2} - нәруыздар

B 3 − к ө м і р л е р {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ B}_{3} - көмірлер

B 4 − с у л а р {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ B}_{4} - сулар

B 5 − д ә р у м е н д е р {\ \ B}_{5} - дәрумендер

Қалыпты:

b 1 b_{1}

b 2 b_{2}

b 3 b_{3}

b 4 b_{4}

b 5 b_{5}

Тағам түрлері:

a 11 a_{11}

a 21 a_{21}

a 31 a_{31}

a 41 a_{41}

a 51 a_{51}

a 12 a_{12}

a 22 a_{22}

a 32 a_{32}

a 42 a_{42}

a 52 a_{52}

Құнарлы өнімдер: Құны
Қалыпты:
Тағам түрлері: с 1 с_{1}
с 2 с_{2}

Әрі қарай π i \pi_{i} түріндегі тағамдардың жалпы құны c i c_{i} -ді құрайды. Адам ағзасын күндік нормасы құнарлы заттардың барлық түрін алатындай жалпы ең кіші болатын жоспарды ұһқұруымыз керек. B i ( i = 1 , 2 , … 5 ) B_{i}(i = 1, 2, \ldots 5) .

x 1 ж ә н е x 2 x_{1}{және\ x}_{2} - π 1 ж ә н е π 2 {\ \ \pi}_{1}{\ және\ \pi}_{2} -дегі тағам түрлерінің мөлшері болсын. Бұл жағдайда екі түрлі тағамдағы майлардың қоры

a 11 x 1 + a 12 x 2 a_{11}x_{1} + a_{12}x_{2}

және b 1 b_{1} минималь нормасынан аз болуы тиіс. Бұл талап

a 11 x 1 + a 12 x 2 ≥ b 1 . a_{11}x_{1} + a_{12}x_{2} \geq b_{1}.

теңсіздігіне алып келеді.

Теңсіздектегі таңбалар тамақтану жүйесіндегі қолданылатын майлар ең кіші нормасынан көбірек болғандығын көрсетеді. Сонымен осы жағдайлардан

a 21 x 1 + a 22 x 2 ≥ b 2 , a_{21}x_{1} + a_{22}x_{2} \geq b_{2},

a 31 x 1 + a 32 x 2 ≥ b 3 , a_{31}x_{1} + a_{32}x_{2} \geq b_{3},

a 41 x 1 + a 42 x 2 ≥ b 4 , a_{41}x_{1} + a_{42}x_{2} \geq b_{4},

a 51 x 1 + a 52 x 2 ≥ b 5 . a_{51}x_{1} + a_{52}x_{2} \geq b_{5}.

төрт теңсіздіктер жүйесіне келеді.

Сонымен F F тамақтанудың жалпы құны

F = c 1 x 1 + c 2 x 2 . F = c_{1}x_{1} + c_{2}x_{2}.

тең. Демек біз келесі математикалық есепке орлайық.

a i 1 x 1 + a i 2 x 2 ≥ b i a_{i1}x_{1} + a_{i2}x_{2} \geq b_{i}\ \ ( i = 1 , … , 5 ) (i = 1, \ \ldots, 5) (1. 1. 8)

x 1 , x 2 x_{1}, x_{2} айнымалы бес сызықтық теңсіздік және

F = c 1 x 1 + c 2 x 2 F = c_{1}x_{1} + c_{2}x_{2} (1. 1. 9)

сызықтық форма жүйесімен берілген.

8-жүйеден барлық теріс емес шешімдердің арасынан F- формасы ең кіші мәнге ие болатындығын табу керек.

1. 2 НЕГІЗГІ ЕСЕП ЖӘНЕ НЕГІЗГІ ТҮСІНІКТЕР.

Сызықтық программалаудың негізгі есептері келесі түрде болады

a 11 x 1 + … + a 1 n x n = b 1 , a 21 x 1 + … + a 2 n x n = b 2 , . . . . . . . . . . . . . . . . a m 1 x 1 + … + a m n x n = b m . } \left. \ \begin{array}{r} a_{11}x_{1} + \ldots + a_{1n}x_{n} = b_{1}, \\ a_{21}x_{1} + \ldots + a_{2n}x_{n} = b_{2}, \\ . \ \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \ \ . \\ a_{m1}x_{1} + \ldots + a_{mn}x_{n} = b_{m}. \ \end{array} \right\} (1. 2. 1)

m- сызықтық алгебралық теңдеулер n белгісіз x 1 … x n x_{1}\ldots x_{n} айнымалылардан туратын жүйе берілген және осы белгісіздерге қатысты сызықтыө форма

F = c 1 x 1 + … + c n x n + c 0 F = c_{1}x_{1} + \ldots + c_{n}x_{n} + c_{0} (1. 2. 2)

түрде жазылады.

(1. 2. 1) берілген жүйеден барлық теріс емес шешімдердің арасынан F F сызықтық форма ең кіші мәнге ие болатын шешімді таңдау керектігін талап етеді.

Анықтама 1. 1 (1. 2. 1) жүйені берілген есептің шектеулер жүйесі деп атаймыз.

Ескерту 1. 1 Есепте x 1 , x 2 , … , x n x_{1}, x_{2}, \ldots, x_{n} белгісіздері тек қана теңдікті емес, сонымен қатар теңсіздікті де қанағаттандыруы тиіс.

Ескерту 1. 2 Ең маңызды жайт (1. 2. 1) теңсіздктегі шектеулер шындыңында негізгі есептегі барлық шектеулерді қамтымайды, себебі x 1 , x 2 , … , x n x_{1}, x_{2}, \ldots, x_{n} айнымалылар теріс шартты қанағаттандырмауы міндетті

x 1 ≥ 0 … x n ≥ 0 x_{1} \geq 0\ldots x_{n} \geq 0

Анықтама 1. 2 (1. 2. 1) жүйенің барлық теріс емес x 1 ( 0 ) , … , x n 0 ( x i ( 0 ) ≥ 0 ; i = 1 , … , n ) x_{1}^{(0) }, \ldots, x_{n}^{0}\ (x_{i}^{(0) } \geq 0; i = 1, \ldots, n) шешімдерін мүмкін шешімдер деп атаймыз.

Анықтама 1. 3 (1. 2. 1) жүйенің F F формасын минималдаушы теріс емес шешімдерін минималдаушы оптималды деп атаймыз.

... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Сызықтық программалаудың есептері
Сызықты және математикалық программалау
Сызықтық программалау есептері. Көп айнымалы үшін оңтайландыру шарты
Сызықты программалау есептері және оларды шешу әдістері
СЫЗЫҚТЫҚ ПРОГРАММАЛАУ ЕСЕПТЕРІ
Сызықтық программалау есептері және оларды шешу әдістері
Компьютерлік технология көмегімен оптимизациялау әдістері
Екі жақтылық есебі
«Транспорттық тапсырма»
Программалауға кіріспе. Алгоритмдеу есептерінің негіздері. Алгоритмдер. Практикалық сабақтарға арналған әдістемелік нұсқаулар
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz