Дифференциалдық геометрия және топология

«ДИФФЕРЕНЦИАЛДЫҚ ГЕОМЕТРИЯ ЖӘНЕ ТОПОЛОГИЯ»

пәні бойынша оқу-әдістемелік кешені

050109 - Математикаа

мамандығы үшін

Семей

2013

Құрастырған доцент Нақышбекова Ғ. М.

Кафедра мәжілісінде мақұлданды

« 31 » 08 2013ж. Хаттама № 1

Кафедра меңгерушесі доцент Жолымбаев О. М.

Факультеттің оқу -әдістемелік кеңесінде мақұлданды

« » 2013 ж. Хаттама №

Оқу әдістемелік кенесінің төрайымы проф. Токабаева Г. К.

Факультеттің ғылыми кеңесінде мақұлданды

« » 2013ж. Хаттама №

Факультет деканы проф. Берікханова Г. Е.

1. ПӘННІҢ ОҚУ БАҒДАРЛАМАСЫ - SYLLABUSОқытушылар туралы мәлімет:

Нақышбекова Ғафиза Молдабекқызы - доцент

Оқытушымен байланыс: СМПИ, корпус 3, аудитория 226

Тел. 64-62-09

2. Пән туралы мәліметтер:

«Дифференциальдық геометрия және топология»

Кредит саны - 2

Жүргізілетін орны № 3 корпус

Оқу жоспарынан көшірме:

3. Курстық пререквизиттері (пәнге қажет білім) ; Бұл пәнді толық меңгеру үшін, аналитикалық геометрияның негізгі бөлімдерін, математикалық талдаудағы бір және көп айнымалы функциялардың дифференциальдық есептеулерін және интеграл теориясын білу қажет.
4. Курстың постреквизиттері. Бұл курстың материалы математикалық анализде, дифференциялдық теңдеулерде және математикалық физиканың теңдеулерінде қолданылады.
5. Курстың қысқаша сипаттамасы; Бұл курс «математика» мамандығының студенттеріне арналған.

Курстың мақсаты: Дифференциалдық геометрия курсының негізгі теориялық бөлімдерін оқып үйрену.

Геометрия оқыту келесі бағыттарды

• логикалық және алгоритмдік ойлауды дамытуды;
• геометриялық есептерді шешу мен зерттеу әдістерін игеруді;
• математикадағы сандық әдістерді игеруді;
• өздігінен білімін кеңейту және қолданбалы (инженерлік) есептерді талдай білуді;
• Топология элементтері және метрикалық, топологиялық кеңістіктер туралы мәлімет;
• Топологиялық бейнелеу, гомеоморфизм, қарапайым беттерді

оқытуды мақсат етеді.

Курстың міндеті:

Пәнді оқытудың негізі - ақпараттық жүйелер мамандығы бойынша мамандар дайындаудағы жоғарғы кәсіби білім мемлекеттік стандарты орнатқан талаптарды орындау (жүзеге асыру) .

Пәнді оқытуда келесі міндеттер қойылады:

а) Студенттерді өздерінің практикалық ж±мыстарында есептеу єдістерін қолдана білуге үйрету;

б) Студенттердің жалпы математикалық білім деңгейін жетілдіру, пєн бойынша жүйелі білімді қалыптастыру;

в) Математикалық есептерді зерттеуде, талдауда болашақ мамандардың шығармашылық ойлау деңгейін дамыту;

г) Студенттерді оқу және ғылыми әдебиеттермен өздігімен жұмыс істеуге үйрету.

Пәнді оқып, үйрену нәтижесінде студенттер мыналарды білуге міндетті :

• вектор-функциялар ұғымы және оларға амалдар қолдану;
• қисықтар ұғымы және оның негізгі теңдеулері;
• беттер ұғымы және оның негізгі теңдеулері.
• Топология элементтері және метрикалық, топологиялық кеңістіктер туралы мәлімет;
• Топологиялық бейнелеу, гомеоморфизм, қарапайым беттер.

6. Пән бойынша тапсырмалардың орындалу және тапсырылу графигі

Әдебиеттер тізімі: Негізгі әдебиеттер

1. Базылев В. Т. Геометрия. 2-б. Алматы - 1981.
2. Атанасян А. В. , Гуревич Г. Б. Геометрия. Ч. 2. М. 1977.
3. Рашевский П. К. Курс дифференциальной геометрии. М. 1956.
4. Васильев А. М., Соловьев Ю. П. Дифференциальная геометрия. М., МГУ, 1981.
5. Бляшке В. Введение в дифференциальную геометрию. М. 1957.
6. Моденов Л. С. Сборник задач по дифференциальной геометрии. М. 1953.
7. Атанасян Л. С. Сборник задач по геометрии. М. 1975.
8. Қожашева Г. О. Дифференциалдық геометрия есептері мен жаттығулары. Талдықорған - 2007.
9. Погорелов А. В. Дифференциальная геометрия. - М., Наука, 1969.
10. Мищенко А. С., Соловьев Ю. П., Фоменко А. Т. Сборник задач по дифференциальной геометрии и топологии. - МГУ, 1981.
11. Норден А. П. Краткий курс дифференциальной геометрии. - М. 1958.

Рейтинг-шкала

8. Курстың саясаты және процедуралары

Студент оқытылатын лекция курсын қысқаша мазмұнын жазып отыруы тиіс, практикалық және үй тапсырмаларын орындауы, сабаққа кешікпей келуі керек, сабақ уақытында сөйлеспеуі, газет-журнал оқымауы, ұялы телефонды ағытып қоюы және оқу процесіне белсенді қатысуы тиіс. Бақылау жұмыстарын, коллоквиумдарды, емтихандарды уақытылы тапсыруы тиіс. Студент сабаққа міндетті түрде қатысуы қажет. Себепсіз босатылған сабақты студент оқу-әдістемелік кешенінде көрсетілген сабақ көлеміне сәйкес қайта тапсырылады. Курстың үштен бір бөлігін себепсіз босату оқудан шығарып жіберуге әкеледі.

2. ПӘН БОЙЫНША ОҚУ-ӘДІСТЕМЕЛІК МӘЛІМЕТТЕРКурстың тақырыптық жоспары

Барлығы 2 кредит

2. 1. Лекция сабағының тақырыптары

Лекция тақырыбы. Вектор - функциялар ұғымы.

Векторлық есептеулер екі бөлімнен тұрады: векторлық алгебра және векторлық анализ.

Векторлық алгебраның элементтері вевлитикалық геометрия курсында қаралады. Мұнда вектор ұғымы және оларға қолданылатын амалдар: векторларды қосу, азайту, векторды скалярға көбейту, векторлардың скаляр көбейтіндісі, векторлардың векторлық көбейтіндісі, векторлардың аралас көбейтіндісі қарастырылады. Бұл амалдардың барлығы тұрақты векторлар үшін енгізілген.

Векторлық анализ айымалы векторларды қарастырып, шектер мен дифференциалды есептеу теорияларын құра отырып, векторлық функцияларды оқиды. Скаляр аргументті функция ұғымы векторлық анализдің негізгі туынды ( алғашқы) ұғымы болып табылады.

∀t∈L, 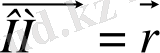векторының басы О нүктеде, t=1 t=2

ұшы М(t) нүктеде жатады. Сондықтан. M(t)

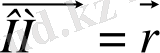вектор t уақыттағы функция болады.

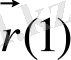
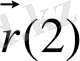
Көптеген қолданбаларда векторлар үстіндегі сызықтық амалдардың жеткіліксіз екендігі байқалады. Күш жұмысы ұғымы, сол сияқты сызықтық жылдамдық пен айналатын қатты дене нүктесінің радиус-векторы арасындағы байланысты тек (векторларға қолданылатын) бинар операциясы көмегімен өрнектеуге болады. Мұндай операциялардын қасиеттері сандар көбейтіндісі операциясының қасиеттеріне ұқсас.

Келтірілген жағдайдың бірінде операция нєтижесі сан болса, екіншісінің нєтижесі вектор. Осы операциялардың жақсы танымалы анықтамаларын келтірейік.

Анықтама. 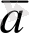жєне 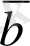векторларының скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыш косинусының көбейтіндісіне тең санды айтады.

Скаляр көбейтіндісін ( 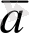, 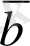) арқылы белгілеп, бұл анықтаманы

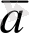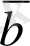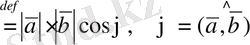( , ) (11) түрінде жазуымызға болады.

Нөлдік көбейткіштері үшін ( 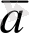, ) 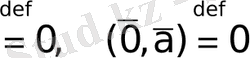(12)

Қасиеттері:

1. (, ) =(, ) (13)

скаляр көбейтіндісінің ауыстырымдылығы және скалярға көбейтуге қатысты

2. ( 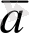, 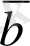) = 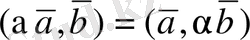(14)

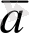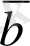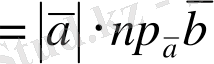3. ( , ) (15)

4. 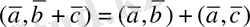(16) - үлестірімділік қасиеті

5. 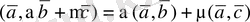(17)

Скаляр көбейтінді өзінің әрбір көбейткішіне қатысты сызықты.

Сонымен бірге нольден өзгеше векторлардың скаляр көбейтіндісінің нольге айналуы сол векторлардың перпендикулярлығының айғағы. Бұдан

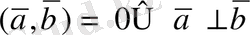(18) шығады.

Шынында, ( 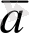, 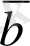) 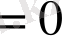теңдігінен (11) формула бойынша 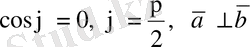екендігі шығады.

Керісінше,

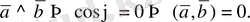
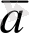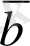Анықтама. Нольден өзгеше және векторларының векторлық көбейтіндісі деп төмендегі үш қасиетпен анықталатын 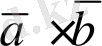векторын айтады:

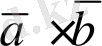
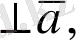
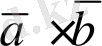
1) 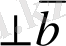атап айтқанда көбейтінді көбейткіштерге перпендикуляр;

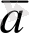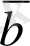
2) , 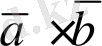векторлар үштігі декарт базисінің үштігімен бірдей ориентацияланған

3-сурет

3) (19)

Бұл анықтамадан векторлық көбейтіндінің нольге тең болуы олардың коллинеарлығын білдіретіні шығады.

Векторлық көбейтіндінің қасиеттері:

1. (20) - антикомутативті
2. () =(21)
3. (22) - үлестірімділік заңы

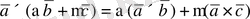(23) - біріктіру заңы

(17), (20), (23) формулаларына сүйене отырып скаляр және векторлық көбейтінділерінің, көбейткіштердің координаталары арқылы өрнектелуін шығарып алу қиын емес.

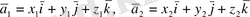
векторларына қолданып

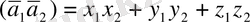(24)

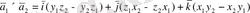(25)

формулаларына келеміз. Соңғы формуланы

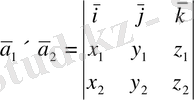(26)

түрінде жазуға болады.

Енді үш

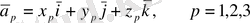(27)

векторын қарастырайық. 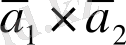векторын 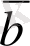арқылы белгілеп

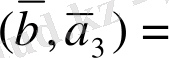
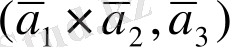
көбейтіндісін есептейік. (26) және (24) формулаларын пайдаланып мынаны аламыз:

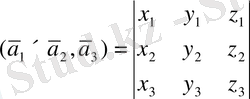(28)

Мұнан 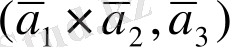= 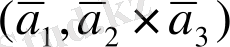шығады, сондықтан

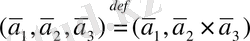(28 ₁ )

анықтамысын енгізген орынды.

Әдетте үш вектордың мұндай көбейтіндісін аралас немесе векторлы-скаляр көбейтінді дейді.

Үш вектордың сызықтық тәуелділігі олардың компланарлығын білдіретіндіктен, сонымен бірге (28) анықтауышы жолдарының сызықтық тәуелділігін білдіретіндіктен, үш вектордың аралас көбейтіндісінің нольге айналуы олардың компланарлығымен мәндес деп айтуымызға болады.

Сонымен 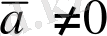жағдайында:

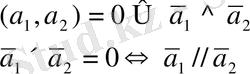
компланар - .

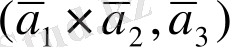
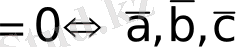Соңында аралас көбейтіндінің геометриялық мағынасын ашайық.

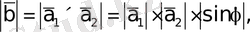саны

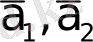
векторларында салынған параллелограммның S ауданы болғандықтан, ал 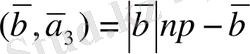және 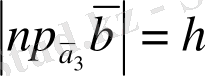(мұндағы һ-қырлары 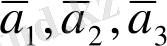параллелепипедінің биіктігі), онда

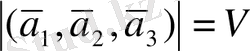
мұнда V -сөз етіліп отырған параллелепипедтің көлемі.

Негізгі әдебиеттер:[1-5]

Қосымша әдебиеттер:[6-7]

Лекция тақырыбы Скаляр аргументті вектор-функциялар.

Бір және екі скаляр аргументті вектор-функциялар. Келбет.

Векторлық анализде сандар жиыны мен бірге векторлар жиыны елеулі орын алады.

Бұл векторлар жиыны аргументтер жиыны болуы да мүмкін, мәндер жиыны болуы да мүмкін. Сондықтан функциялардың жаңа 3 түрі пайда болады.

1. 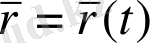- скаляр аргументті вектор-функциялар.

2. 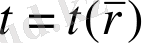- вектор аргументті скаляр функциялар.

3. 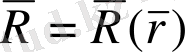- вектор аргументті вектор-функциялар.

Бұл жағдайлардың әрқайсысында аргумент ретінде бір сан (бір вектор) емес, сандардың (немесе векторлардың) реттелген бумасы болуы мүмкін.

2-ші және 3-ші типтес функциялар келесі тарауда зерттеледі. Әзірше скаляр аргументті вектор-функцияларға назар аударайық. Бұл функцияларды геометриялық тұрғыдан зерттеу келбет ұғымына сүйенеді.

Бір немесе екі аргументті вектор-функциясының барлық мәндері болып келетін радиус-векторлар ұштарының геометриялық орны осы функцияның келбеті деп аталады.

M(x, y, z) нүктесінің радиус-векторы оның координаталары және 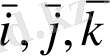(тұрақты) базистік векторлары арқылы

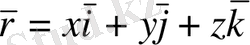(1)

түрінде өрнектелсе, онда

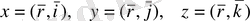(2)

Демек бір вектор фукцияның берілуі үш скаляр x, y, z функцияларының берілуіне мәндес. Бір скаляр аргумент жағдайында

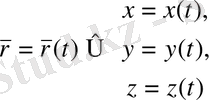(3)

t параметрінен құтылып (ол тек 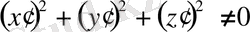болуында мүмкін)

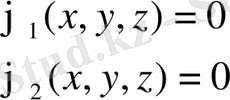(4)

қатынастарын аламыз.

Мұнан бір аргументті вектор-функция годографы қисық (екі беттің қиылысу сызығы) болатыны шығады.

Екі аргумент үшін

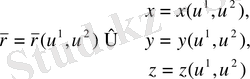(5)

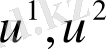айнымалыларынан құтылу.

(Ол 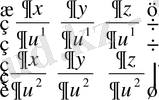(6) матрицасының рангі екіге тең болуында ғана мүмкін), екі аргументті вектор-функция келбетінің бет екенін көрсетеді, өйткені (5)

z=z(x, y) (7)

түрінде келеді.

Негізгі єдебиеттер:[1-5]

Қосымша єдебиеттер:[6-7]

Лекция тақырыбы

Үзіліссіздік пен дифференциалдану.

Туындылардың геометриялық мағынасы.

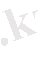
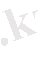Анализдің негізгі ұғымдарын скаляр аргументті вектор-функцияларға тарату қиын емес.

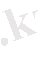Ең алдымен айнымалы 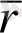векторларының шегі деп

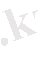
(8)

теңдігін қанағаттандыратын тұрақты 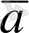векторын айтамыз. Осымен бірге вектордың шек ұғымы 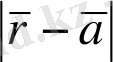скаляр айнымалының шек ұғымына келтіріледі.

Сонымен

(9)

Шек теориясының негізгі теоремалары оп-оңай дәлелденеді. Олар қысқаша былай тұжырымдалады.

Теорема . Егер 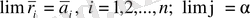болса онда келесі шектер бар болып мына түрде есептелінеді.

(10)

мұнан «қанатты» ережеге келеміз: қосынды (немесе көбейтінді) шегі шектер қосындысына. (немесе көбейтіндісіне) тең.

Енді функциясының мәніндегі үзіліссіздігін анықтаған оп-оңай. Ол

(11)

теңдігінің орындалғанын білдіреді.

Егер (11) барлық a<t<b үшін орындалса, 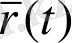функциясы (a, b) аралығында үзіліссіз делінеді.

(1), (2), (10) және (11) -ден 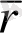функциясының үзіліссіздігінің x, y, z функцияларының үзіліссіздігімен эквиваленттілігі шығады.

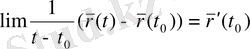(12)

шегіне ие болатын 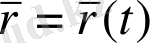функциясын 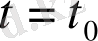мәнінде дифференциалданатын функция ал осы шектің мәнін 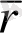функциясының 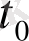нүктесіндегі туындысы дейді. a<t<b аралығының барлық нүктелерінде дифференциалданатын функциясын осы интервалда дифференциалданатын функция делініп, ал 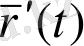функциясы осы интервалдың барлық нүктелерінде анықталған болып келеді.

Векторлардың қосындысы және көбейтіндісі шегінің теоремаларына сүйенсе қосындыны және көбейтіндіні дифференциалдау ережелері скаляр анализдегідей болады:

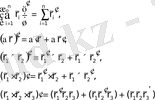(13)

Әрине векторлық және аралас көбейтіндідегі көбейткіштердің орнын ауыстыруға болмайды, өйткені .

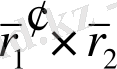
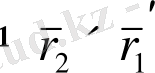Сол теоремалардың арқасында күрделі функцияны дифференциалдау ережесі бұрынғыша сақталады

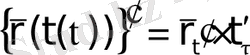(14)

(төмендегі 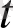немесе 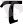индексі дифференциалдауды қандай аргумент бойынша жүргізу керек екенін көрсетеді)

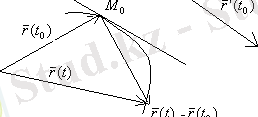4-сурет.

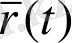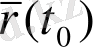және векторларының ұштары вектор-функция келбетінің нүктелері болады.

Сонда олардың ұштарын қосатын 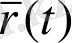- 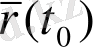векторы хордаға, ал оның шектік орналасуы 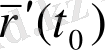жанамасына параллель. Сонымен туынды бағытының геометриялық мағынасы ашылды, ол 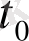нүктесінде келбеттің жанамасын анықтайды. Жанаманың теңдеуін (І тараудың (35) теңдеуімен салыстырыңыз)

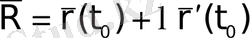(15)

түрінде жазуға болады. Мұнда 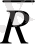-жанама айнымалы нүктесінің радиус-векторы, -параметр.

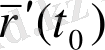векторының ұзындығы t параметрінің алынуына тәуелді және оны ауыстырғанда өзгереді. Шынында

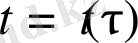(16)

жаңа 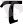параметріне көшсек, 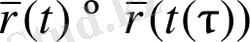функциясының

нүктесі аймағындағы мәндері өзгермейді, атап айтқанда қисық пен оның М ₀ , нүктесіндегі жанамасы сол беті (сол күйі) сақталады. Бірақ (14) -ке сәйкес

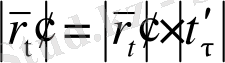
яғни, жалпы алғанда, 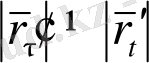. (16) бойынша 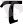параметрінің келіскен бір алынуында 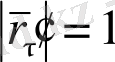болады. Параметрдің мұндай алынуының қарапайым геометриялық мағынасы бар.

Расында

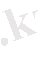
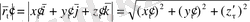
болғандықтан

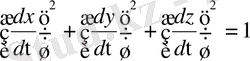
және

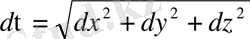
Қисықтың доға ұзындығы

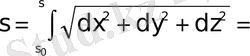
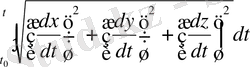
формуласы бойынша есептелетіндігі мәлім.

Демек

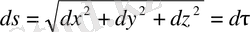, (17)

атап айтқанда, вектор-функция туындысының модулі, оның аргументі қисықтың доға ұзындығы болғанда ғана бірге тең.

Бірнеше аргументті вектор-функциялардың үзіліссіздігі мен дифференциалдануы ұғымдары анализдегі скаляр функциялардың сәйкес ұғымдарына ұқсас енгізіледі. Мәселен, екі аргументті

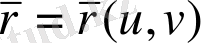(18)

функциясының дербес туындысы кәдімгі анализдегідей анықталады.

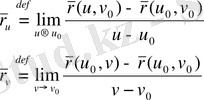(19)

Олардың геометриялық мағынасын анықтау үшін 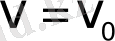шарты (18) функциясы келбетінде

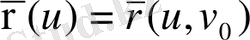
қисығын бөліп алатынын байқаған жөн, 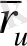туындысы осы қисықтың жанамасына параллель. Дәл осы сияқты 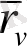векторы сызығының жанамасына параллель.

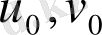қос санының берілуі бет нүктесін анықтайтындықтан, u, v параметрлері бет нүктесінің қисықсызықты координаталары деп, ал u=const жєне v=const сызықтарын координаталық сызықтар атаған.

x, y, z функциялары үшін жазылған Тэйлор формулаларын және (1) жіктемесін пайдаланып, 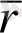функциясының да Тэйлор қатарына жіктелетінін аламыз. Мәселен, бір айнымалыға тәуелді функция жағдайында

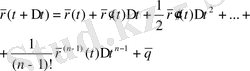(20)

мұнда 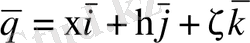, ал 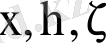мүшелері - x, y, z -ке жазылған Тэйлор қатарларындағы қалдық мүшелері. 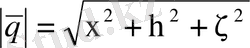өрнегі шектеулі болғандықтан, (20) қатарындағы қалдық мүшесінің кішілік реті n санынан кем емес, оны былай жазатын боламыз

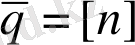(21)

n=2 мєнінде (20) -дан алатынымыз

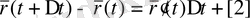(22)

Оң жағындағы бірінші қосылғыш вектор-функция өсімшесінің басты сызықтық бөлігі болып табылады, ол вектор-функция дифференциалы деп аталып

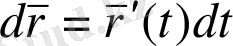(23)

арқылы белгіленеді. Екі айнымалы жағдайында

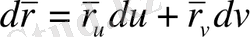(24)

Екінші, үшінші жєне жоғары ретті дифференциалдардың формулалары анализдегідей. Кейде

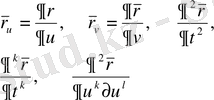белгілеулері кездеседі.

Негізгі єдебиеттер:[1-5]

Қосымша єдебиеттер:[6-7]

Лекция тақырыбы. Сызықпен байланысқан негізгі дифференциоалды-геометриялық ұғымдар.

1. Параметірленген қисық. Егер қисық берілсе, оның бойымен уақыт арасында ағымды М нүктесі қозғалады деп есептеуімізге болады. Уақыттың әр бір t сәтінде бұл нүкте қисықтта белгілі орын алады, атап аәтқанда ағымды М нүктесінің радиус-векторы t параметрін

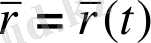
параметірі түрінде жазылған фукциясы болады. Керісінше, егер ағымды М нүктесінің 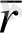радиус-векторы қандай да t скаляр параметрінің функциясы ретінде берілсе, оның ұшы қисық сызық сызады. Басқаша айтқанда қисық 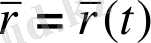вектор-функция келбеті ретінде анықталады .

Анықтама. Егер қисықтың ағымды М нүктесінің радиус-векторы қандай-да (a, b) аралығында өзгеретін t скаляр параметрінің үзіліс функциясы ретінде анықталған болса, қисық параметрленген ал

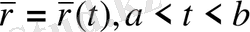
оның векторлық теңдеуі делінеді.

" Қисықты", "сызық " немесе "қисық сызық" деп те айта береді.

Егер t параметірін оның 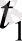параметіріне түрлендірсе, сол қисықтың жаңа

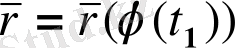(мұндағы )

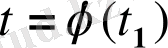теңдеуі алынады. Сонымен бірден-бір қисық түрлі теңдеулермен анықталуы мүмкін.

Мәселен

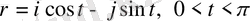
және

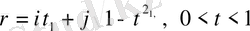
теңдеулері бірен-бір жарты шеңберді анықтайды. Бұл жағдайда 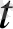және 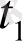параметрлері 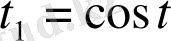қатынасымен байланысады.

2. Жанама. Сызықпен байланысқан қарапайым дифференциал-геометриялық ұғымға бізге таныс жанама жатады.

... жалғасы

XIII ғасырға дейінгі Еуропа математикасы

Сызық инварианттарының есептеу формулалары

Өскелең ұрпаққа білім мен тәрбие беру мәселесі

Математиканың даму тарихы

Дифференциалдық геометрия

Түйіндес түрлендірулер

Күрделі сызықтардық қисықтықтары мен бұралымдары

Мектепке жасына дейінгі балалардың математикалық түсініктерін дамытуда дидактикалық ойындарды қолдануға сипаттама

Төлеубай Ыдырысұлы Аманов - Қазақстандағы функциялар теориясы және функционалдық анализ мектебінің негізін салушы ғалым

Геометриялық есептерді шешу

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс