Теңдеудің Галуа тобының есептелуі


Абай атындағы Қазақ Ұлттық Педагогикалық Университеті
физика - математика факультеті
Алгебра, геометрия және қолданбалы логика кафедрасы
Түлектік жұмыс
Теңдеудің Галуа группасын есептеу
Орындаған Ражапова Г. С
4 курс студенті
Ғылыми жетекші Кенжебаев С
ф. м. ғ. к, доцент
Қорғауға жіберілді
кафедра меңгерушісі:
ф. м. ғ. к, профессор Байсалов Е. Р
«__» 2008ж
Алматы 2008ж
Теңдеудің Галуа группасын есептеу
Мазмұны:
Кіріспе 3
- Өрістердің нормальды өсімшелері және Галуа группасы 4
- Симметриялы группалар 17
- n - дәрежелі алмастырулар группасын n - айнымалыдан туратын 21 көпмүшеліктер арқылы анықтау. Алмастырулардың түйіндес группалары
- Кез келген көпмүшеліктің Галуа группасын есептеу. Галуа группасы таңбасы өзгермелі группаның ішкі группасы болатын теңдеу 24
- Үшінші және төртінші дәрежелі теңдеулер және дөңгелектегі көпмүшеліктер 28
Қорытынды 36
Әдебиеттер тізімі 37
Кіріспе
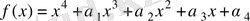
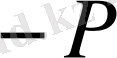 өрісіндегі еселі түбірлері жоқ төртінші дәрежелі кез келген көпмүше.
өрісіндегі еселі түбірлері жоқ төртінші дәрежелі кез келген көпмүше.
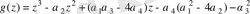 (1)
(1)
Біз келесі төртінші дәрежелі жіктелмейтін көпмүшенің Галуа группасын есептеу қағидасын қарастырамыз.
Егер
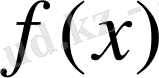 көпмүшесінің дискриминанты квадрат болмасса және
(1)
көпмүшесінің Р өрісінде түбірі болмасса, онда
көпмүшесінің дискриминанты квадрат болмасса және
(1)
көпмүшесінің Р өрісінде түбірі болмасса, онда
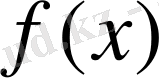 көпмүшсінің Галуа группасы
көпмүшсінің Галуа группасы
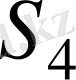 группасы болады.
группасы болады.
Егер
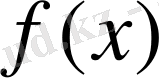 көпмүшесінің дискриминанты квадрат болса, бірақ
(1)
көпмүшесінің Р өрісінде түбірі болмасса, онда
көпмүшесінің дискриминанты квадрат болса, бірақ
(1)
көпмүшесінің Р өрісінде түбірі болмасса, онда
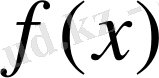 көпмүшесінің Галуа группасы
көпмүшесінің Галуа группасы
 группасы болады.
группасы болады.
Егер
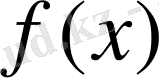 көпмүшесінің дискриминанты квадрат болмасса, бірақ
(1)
көпмүшесінің Р өрісінде ең болмағанда бір түбірі табылса, онда
көпмүшесінің дискриминанты квадрат болмасса, бірақ
(1)
көпмүшесінің Р өрісінде ең болмағанда бір түбірі табылса, онда
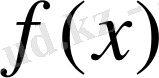 көпмүшесінің Галуа группасы
көпмүшесінің Галуа группасы
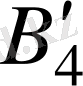 группасына түйіндес.
группасына түйіндес.
Ақырында, егер
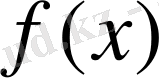 көпмүшесінің дискримнанты квадрат болса және
(1)
көпмүшесінің барлық түбірлері Р өрісіне тиісті болса, онда
көпмүшесінің дискримнанты квадрат болса және
(1)
көпмүшесінің барлық түбірлері Р өрісіне тиісті болса, онда
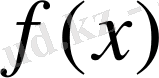 көпмүшесінің Галуа группасы
көпмүшесінің Галуа группасы
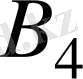 группасы болады.
группасы болады.
Тақырыптың мақсатты: Галуа группасы және теңдеудің Галуа группасын есептеудің мәнін ашу.
Тақырыптың міндеті:
- Симметриялы групалардың мәнін ашу; дәрежелі алмастырулар группасынайнымалыдан туратын
көпмүшеліктер арқылы анықтау. Алмастырулардың түйіндес группалары
- Кез келген көпмүшеліктің Галуа групасын есептеу. Галуа группасы таңбасы өзгермелі группаның ішкі группасы болатын
теңдеу.
- Үшінші және төртінші дәрежелі теңдеулер және дөңгелектегі
көпмүшеліктер.
Зерттелу деңгейі.
Теңдеулердің Галуа группасын есептеу тақырыбына арналған зерттеу жұмысын бірінші болып жазған Эварист Галуа. Галуаның негізгі зерттеулері алгебраға арналады. 3 - ші, 4 - ші дәрежелі теңдеулерді шешу әдістері
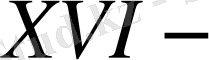 ғасырда белгілі болған.
ғасырда белгілі болған.
 ғасырда Абель, дәрежесі
ғасырда Абель, дәрежесі
 теңдеулердің түбірлерін өрнектейтін жалпы формула табуға болмайтындығын дәлелдеді. Галуа берілген теңдеуді қанағаттандыратын шарттарды анықтады.
теңдеулердің түбірлерін өрнектейтін жалпы формула табуға болмайтындығын дәлелдеді. Галуа берілген теңдеуді қанағаттандыратын шарттарды анықтады.
Группа теориясындағы әдіс және идеялар жаратылыстану, кванттық механика, кристаллографияда қолданыс тапқан.
Постников Г. Г. « Теория Галуа», неміс ғалымы ван дер Варден Б. Л. «Алгебра» атты кітаптар осы тақырыпқа арналған.
Зерттеу жұмысының көлемі. Кіріспе, 5 - тақырыптан, қорытынды, әдебиеттер тізімі, жалпы беттен турады.
Өрістердің автоморфизмдері
Егер өзара бірмәнді
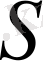 бейнелеуі К өрісіне қосындыны қосындыға, көбейтіндіні көбейтіндіге бейнелесе, яғни егер К өрісіндегі кез келген
бейнелеуі К өрісіне қосындыны қосындыға, көбейтіндіні көбейтіндіге бейнелесе, яғни егер К өрісіндегі кез келген
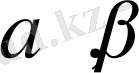 элементтері үшін
элементтері үшін
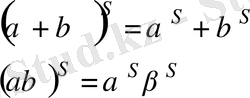 (1)
(1)
(S автоморфизмі
 элементін
элементін
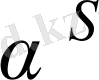 элементіне көшіреді) .
элементіне көшіреді) .
Онда кейбір К өрісінде S бейнелеуі автоморфизм деп аталады. Автоморфизм өзара бірмәнді сәйкестік болу керек, яғни (1) шарттан тыс, ол сондай ақ келесі шарттарды міндетті түрде қанағаттандыру тиіс.
а) Кез келген
 элементтері үшін
элементтері үшін
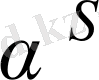 элементі бірмәнді анықталған және
элементі бірмәнді анықталған және
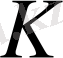 - ға тиісті;
- ға тиісті;
б) Егер
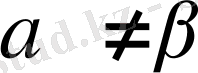 , онда
, онда
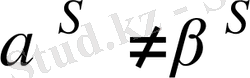 ;
;
в)
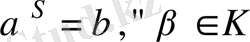 Equation. 3 элементтері үшін
Equation. 3 элементтері үшін
 элементі табылады.
элементі табылады.
в) шартынан б) шартымен қарастырылған
 элементінің бірмәнді екені анықтамадан шығады. Сондықтан бұл элементті
элементінің бірмәнді екені анықтамадан шығады. Сондықтан бұл элементті
 арқылы белгілеп:
арқылы белгілеп:
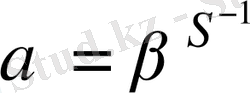 ,
,
біз кейбір
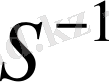 түрлендіруін аламыз. Кез келген
түрлендіруін аламыз. Кез келген
 эементі үшін
эементі үшін
 (2)
(2)
бұл түрлендіру бір мәнді сипатталады.
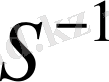 түрлендіруі сондай ақ автоморфизм болады. Шынында да, кез келген
түрлендіруі сондай ақ автоморфизм болады. Шынында да, кез келген
 және
және
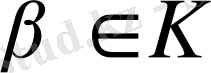 элементтері үшін
элементтері үшін
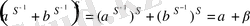
сондықтан, анықтама бойынша төмендегідей болады.
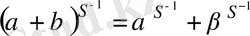
S және T автоморфизмінің ST көбейіндісі түрлендіру деп аталады, нәтижеде алдымен S түрленіруі, кейін Т түрлендіруі алынады; кез келген
 элементі үшін
элементі үшін
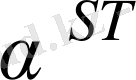 элементі
элементі
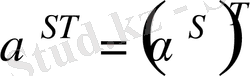
формуласымен анықталады.
Мәселе. Автоморфизмдердің көбейтіндісі ассоциативті екенін дәлелдеу керек.
Автоморфизмдердің көбейтіндісі, анық, бірлікке ие, К өрісінің барлық элементін орнында қалдыратын Е тепе тең автоморфизм атқарады:
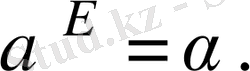
Анықтама бойынша (2 формулаға қарау керек)
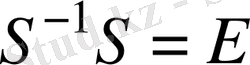 . (3)
. (3)
Енді
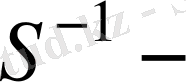 ге кері автоморфизм
ге кері автоморфизм
 автоморфизмін қарастырамыз. Анықтама бойынша
автоморфизмін қарастырамыз. Анықтама бойынша
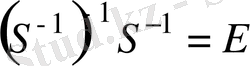 . (4)
. (4)
Бұл теңдіктің оң жағын S- ке көбейтіп және (3) формуланы пайдаланып, біз
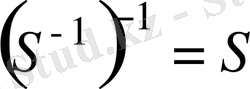
аламыз.
Бұл түрлендіруді (4) формулаға қою арқылы,
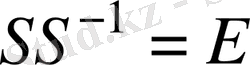
аламыз.
Сонымен,
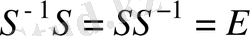 .
.
Біркелкі автоморфизмдердің көбейтіндісі арқылы автоморфизмдердің жиыны группа болатындығын көреміз. Бұл группа К өрісінде автоморфизм группасы деп аталады.
Мәселе. Кез келген автоморфизм рационал сандарды орнында қалдыратынын дәлелдеу керек. (дербес жағдайда, 0 және 1 сандарын) .
Айталық, енді Р - К өрісінде кейбір ішкі өріс болсын. К өрісінде S автоморфизмі Р өрісіндегі автоморфизм деп аталады, егер ол Р өрісінің барлық элементтерін өз орнында қалдырса, яғни егер кез келген
 элементі үшін
элементі үшін
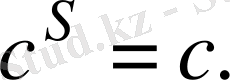
Р өрісідегі барлық автоморфизмдер жиынтығы К өрісінде автоморфизмдер группасының ішкі группасы болады. Егер К өрісі Р өрісінің нормальды өсімшесі болса, онда бұл ішкі өріс Р өрісіндегі К өрісінің Галуа группасы деп аталады және
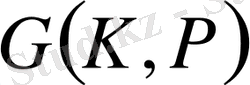 символы арқылы белгіленеді.
символы арқылы белгіленеді.
Айталық
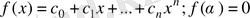
- К - да ең болмағанда
 бір түбірі бар, Р өрісіндегі кез келген көпмүше
бір түбірі бар, Р өрісіндегі кез келген көпмүше
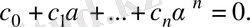 (5)
(5)
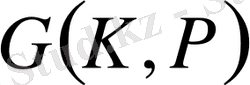 Галуа группасындағы S автоморфизмін (5) тепе теңдікке қолданып, біз келесі
Галуа группасындағы S автоморфизмін (5) тепе теңдікке қолданып, біз келесі
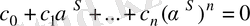
теңдігін аламыз, яғни
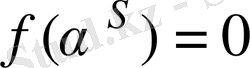 .
.
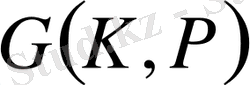 Галуа группасының барлық автомофизмері Р өрісіндегі кез келген көпмүшенің әрбір түбірін қайта осы көпмүшенің түбіріне көшіреді.
Галуа группасының барлық автомофизмері Р өрісіндегі кез келген көпмүшенің әрбір түбірін қайта осы көпмүшенің түбіріне көшіреді.
Бұдан, кез келген
 саны және кез келген
саны және кез келген
 автоморфизмі үшін
автоморфизмі үшін
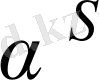 саны К өрісіндегі
саны К өрісіндегі
 саны мен түйіндес блатыны шығады.
саны мен түйіндес блатыны шығады.
Ескерту. Егер сызықтық түрлендіруді белгілі түсінік ретінде қабылдасақ, онда нөлден өзгеше вектор нөлдік векторға ауыпайтын ақырлы кеңістіктің сызықтық түрлендіруі сонда және сонда ғана өзара бірмәнді, сондай ақ кездейсоқ ақырлы өсімше үшін анықтамадағы автоморфизмнің түсінігін шарт бойынша Р өрісіндегі К өрісінің өзара бірмәнді деп көрсетуге болады, яғни (1) қасиетке ие болатын және Р өрісінің барлық элементтерін орнында қалдыратын ақырлы К өсімшесінің кез келген S бейнелеуі өзара бірмәнді, яғни Р өрісіндегі К өрісінің автоморфизмі болып табылады.
Шынында да, егер
 және
және
 , онда
, онда
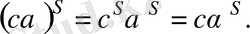
К өрісінің кез келген
 және
және
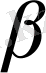 элементтері үшін
элементтері үшін
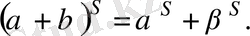
Бұл, Р өрісіндегі қарастырылатын S бейнелеуі К өрісінің сызықтық түрлендіруі болып есептелінетінін білдіреді. Сондықтан, сызықтық түрлендіру теориясынан жоғарыдағы деректе берілгенді дәлелдеу үшін, формула бойынша бекітудің жеткіліктігін көрсетеді, сондай ақ егер
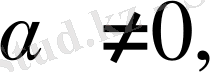 онда
онда
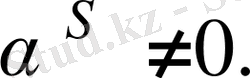 Бірақ егер
Бірақ егер
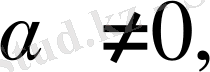 онда К өрісінде мынандай
онда К өрісінде мынандай
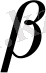 элементі табылады, сондай - ақ
элементі табылады, сондай - ақ
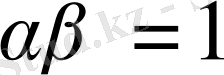 және олай болса,
және олай болса,
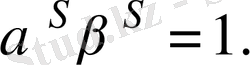 Сонымен,
Сонымен,
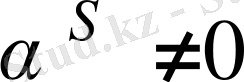 шындық.
шындық.
Галуа группасы туралы түсінік. Галуа теоремасы.
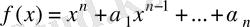 көпмүшелігі берілсін және оның барлық
көпмүшелігі берілсін және оның барлық
 коэфициенттері әлдебір Р өрісіне жатады. Сонда
коэфициенттері әлдебір Р өрісіне жатады. Сонда
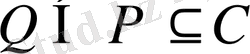 орындалады.
орындалады.
Мысалы, Р -
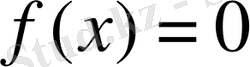 теңдеуінің коэффициенттерінің өрісі, яғни
теңдеуінің коэффициенттерінің өрісі, яғни
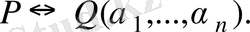
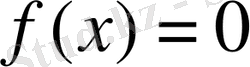 теңдеуінің барлық (нақты және комплекс) түбірлерін
теңдеуінің барлық (нақты және комплекс) түбірлерін
 арқылы белгілейміз.
арқылы белгілейміз.
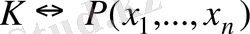 өрісінде f көпмүшелігі бірінші дәрежелі көпмүшеіктердің көбейтіндісінен, яғни
өрісінде f көпмүшелігі бірінші дәрежелі көпмүшеіктердің көбейтіндісінен, яғни
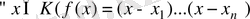
сызықтық көпмүшеліктерінің көбейтіндісінен жіктелетіндігі белгілі. Және керісінше, егер әлдебір К өрісі, мұндағы
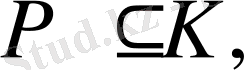 f көпмшелігі сызықты көпмүшеліктердің көбейтіндісімен жіктелетін болса, онда К өрісі
f көпмшелігі сызықты көпмүшеліктердің көбейтіндісімен жіктелетін болса, онда К өрісі
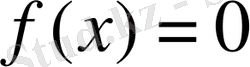 теңдеуінің барлық түбірлерін қамтитындығы айқын.
теңдеуінің барлық түбірлерін қамтитындығы айқын.
Анықтама.
a)
 түріндегі өрісі, мұндағы
түріндегі өрісі, мұндағы
 теңдеуінің барлық түбірлері,
теңдеуінің барлық түбірлері,
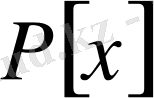 көпмүшеліктерінің сақинасындағы
көпмүшеліктерінің сақинасындағы
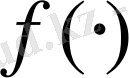 көпмүшелігінің жіктелу өрісі деп аталады. Мұндай f көпмүшелігінің жіктелу өрісін
көпмүшелігінің жіктелу өрісі деп аталады. Мұндай f көпмүшелігінің жіктелу өрісін
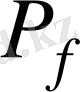 арқылы белгілейміз.
арқылы белгілейміз.
б)
 орындалатындай Р және К екі кез келген өрістер болсын. К өрісінің барлық автоморфизмдерінің жиыны, яғни Р өрісіндегі
орындалатындай Р және К екі кез келген өрістер болсын. К өрісінің барлық автоморфизмдерінің жиыны, яғни Р өрісіндегі
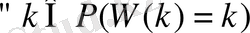

кез келген нүктесі қозғалыссыз болатындай
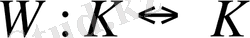 түріндегі барлық изоморфизмдер жиыны Р өрісіндегі К өрісінің Галуа группасы деп аталады.
түріндегі барлық изоморфизмдер жиыны Р өрісіндегі К өрісінің Галуа группасы деп аталады.
Мұндай автоморфизмдер жиынында группаның операция ретінде екі атоморфизмнің композициялық операциясы қарастырылады.
 шартын
шартын
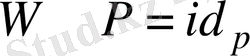 эквивалентті түрде жазуға болады. Р өрісіндегі К өрісінің Галуа группасы
эквивалентті түрде жазуға болады. Р өрісіндегі К өрісінің Галуа группасы
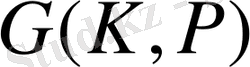 арқылы белгіленеді. Мұнда f функциясына симметриялы элемент
арқылы белгіленеді. Мұнда f функциясына симметриялы элемент
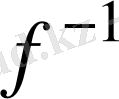 функциясы болып табылады және нейтрал элемент
функциясы болып табылады және нейтрал элемент
 түрдей
түрдей
 тепе теңдік функциясы болып табылады.
тепе теңдік функциясы болып табылады.
в)
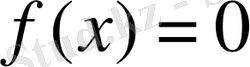 теңдеуінің
теңдеуінің
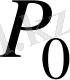 коэффициенттерінің өрісіндегі f көпмүшелігінің
коэффициенттерінің өрісіндегі f көпмүшелігінің
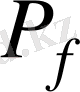 жіктелу өрісінің Галуа группасы, яғни
жіктелу өрісінің Галуа группасы, яғни
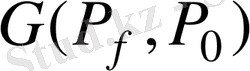 түріндегі Галуа группасы
түріндегі Галуа группасы
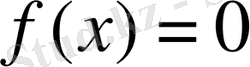 теңдеуінің Галуа группасы деп аталады.
теңдеуінің Галуа группасы деп аталады.
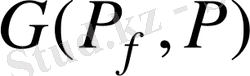 тобы
тобы
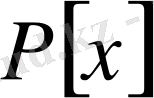 сақинасындағы f көпмүшелігінің Галуа тобы және
сақинасындағы f көпмүшелігінің Галуа тобы және
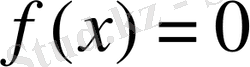 сәйкес теңдеуінің Галуа группасы деп аталады.
сәйкес теңдеуінің Галуа группасы деп аталады.
Галуа группасының маңыздылығын келесі фундаментальды теоремадан және содан кейінгі ескертуден көруге болады:
Э. Галуа теоремасы.
Егер
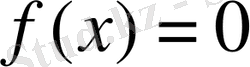 теңдеуінің
теңдеуінің
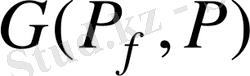 Галуа группасы шешілетін болса, онда
Галуа группасы шешілетін болса, онда
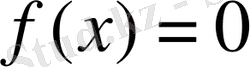 келтірілмейтін теңдеуі, мұндағы
келтірілмейтін теңдеуі, мұндағы
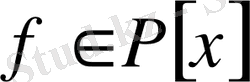 , радикалда шешіледі.
, радикалда шешіледі.
Ескерту. 1. Бұл теорема келесі тұжырымды береді: Галуа группасы көптеген нақты теңдеулер үшін салыстырмалы түрде оңай әрі айқын есептеледі және де ол үшін салыстырмалы түрде оның шешілетіндігі оңай анықталады. Мұндай теңдеулер үшін Галуа теоремасы радикалдағы теңдеудің шешілуі критерийі болып табылады.
2. Галуа теоремасы тек қана келтірілмейтін теңдеулер үшін ғана емес, кез келген теңдеулер үшінде орынды болады. Біз бұл күрделі жағдайды қарастырмаймыз, өйткені кез келген теңдеуді келтірілмейтін теңдеуге айналдыруға болады.
Теорема.
Егер
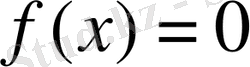 келтірілмейтін теңдеуі, мұндағы
келтірілмейтін теңдеуі, мұндағы
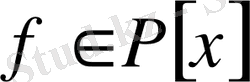 , радикалда шешілетін болса, онда оның
, радикалда шешілетін болса, онда оның
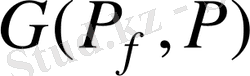 Галуа группасы да шешілетін болады.
Галуа группасы да шешілетін болады.
Бұл теореманың өрнектелу жақсы түсінік беру үшін, алдымен оның қолданылуын, тек содан кейін оның дәлелдеуін қарастырамыз. Бұл теореманы қолдану үшін, біріншіден берілген теңдеудің Галуа группасын есептеуді үйрену қажет. Екінші дәрежелі
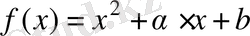 көпмүшелігі үшін де іс жүзінде Галуа группасының қалай табылатыны анық емес. Төменде көптеген нақты көпмүшеліктер үшін Галуа группасын есептеу де мүмкіндік беретін бірнеше ұсыныстар және теоремалар келтірілген. Сонымен бірге, дәлелдеулерде келесі түрдегі көмекші ұсыныстар қолданылады.
көпмүшелігі үшін де іс жүзінде Галуа группасының қалай табылатыны анық емес. Төменде көптеген нақты көпмүшеліктер үшін Галуа группасын есептеу де мүмкіндік беретін бірнеше ұсыныстар және теоремалар келтірілген. Сонымен бірге, дәлелдеулерде келесі түрдегі көмекші ұсыныстар қолданылады.
а)
 түрдегі кез келген өріс
түрдегі кез келген өріс
 нүктеснде анықталан
нүктеснде анықталан
 өрісінен f барлық рацоналды функциясының
өрісінен f барлық рацоналды функциясының
 нүктесінің мәндерінің дәлдігінен тұрады.
нүктесінің мәндерінің дәлдігінен тұрады.
б) Егер
 - К өрісіндегі n дәрежелі келтірілмейтін
- К өрісіндегі n дәрежелі келтірілмейтін
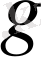 көпмүшелігінің түбірі болса, онда
көпмүшелігінің түбірі болса, онда
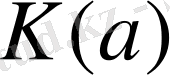 өрісі
өрісі
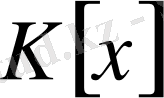 сақинасынан
сақинасынан
 ден кіші немесе тең дәрежелі барлық көпмүшеліктерінің
ден кіші немесе тең дәрежелі барлық көпмүшеліктерінің
 нүктесіндегі мәндерінің дәлдігінен тұрады. К өрісіндегі
нүктесіндегі мәндерінің дәлдігінен тұрады. К өрісіндегі
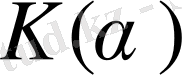 тасымалдауышымен берілген векторлық кеңістігінің өлшемі n санына тең.
тасымалдауышымен берілген векторлық кеңістігінің өлшемі n санына тең.
в)
 сандары Р өрісіндегі қандай да бір көпмүшеліктерінің түбірлері болсын және
сандары Р өрісіндегі қандай да бір көпмүшеліктерінің түбірлері болсын және
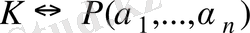 болсын. Онда К өрісіндегі кез келген элемент
болсын. Онда К өрісіндегі кез келген элемент
 сақинасындағы әлдебір көпмүшеліктің
сақинасындағы әлдебір көпмүшеліктің
 нүктесіндегі мәні болып табылады. (
нүктесіндегі мәні болып табылады. (
 сандары Р өрісінде алгебралық деп аталады) .
сандары Р өрісінде алгебралық деп аталады) .
г) Кез келген келтірілмейтін теңдеудің еселік түбірі болмайды.
а) Егер

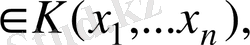 онда
онда

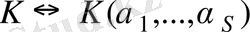 және
және
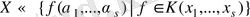 белгілейміз де,
белгілейміз де,
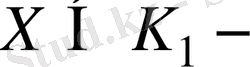 ді аламыз. Х жиыны С - да жатады және сандармен қарапайым операцияға қатысты бұл жиын К өрісін және
ді аламыз. Х жиыны С - да жатады және сандармен қарапайым операцияға қатысты бұл жиын К өрісін және
 сандарын қамтитын өріс болып табылатындығы айқын. Сондықтан
сандарын қамтитын өріс болып табылатындығы айқын. Сондықтан
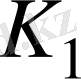 өрісі Х жиынына жатады және де
өрісі Х жиынына жатады және де

б)
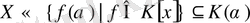 және
және
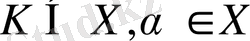 орындалатындығы айқын. Егер Х өрісі болса, онда
орындалатындығы айқын. Егер Х өрісі болса, онда
 және де
және де
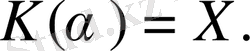 Х жиынының өріс болып табылатындығын тексереміз. Ол үшін егер
Х жиынының өріс болып табылатындығын тексереміз. Ол үшін егер
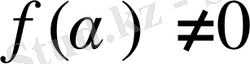 болғанда
болғанда
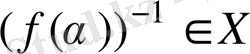 орындалатындығын орнату жеткілікті.
орындалатындығын орнату жеткілікті.
Егер f және g көпмүшеліктері
 1 дәрежелі ортақ бөлгішке ие болса, онда Х келтірілмеген g көпмүшелігінің тривиальды емес бөлгіші бола отырып, К g -ге сәйкес келетін болғандықтан f және g көпмүшеліктері К өрісінде өзара қарапайым болып табылады. Онда
1 дәрежелі ортақ бөлгішке ие болса, онда Х келтірілмеген g көпмүшелігінің тривиальды емес бөлгіші бола отырып, К g -ге сәйкес келетін болғандықтан f және g көпмүшеліктері К өрісінде өзара қарапайым болып табылады. Онда
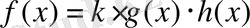 және
және
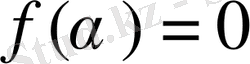 қарама - қайшылыққа кездестік. g және f өзара қарапайым болғандықтан, онда алгебра курстан белгілі теорема бойынша
қарама - қайшылыққа кездестік. g және f өзара қарапайым болғандықтан, онда алгебра курстан белгілі теорема бойынша
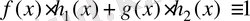
К өрісіндегі
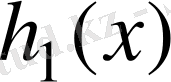 және
және
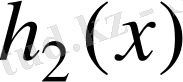 көпмүшеліктері бар болады. Онда
көпмүшеліктері бар болады. Онда
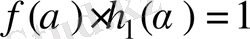 және
және
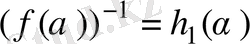 және
және
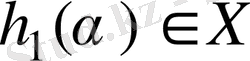 .
.
Сонымен,
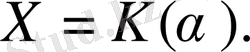
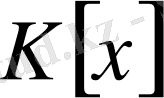 сақинасындағы кез келген f көпмүшелігін g көпмүшесіне қалдықпен болуге болады.
сақинасындағы кез келген f көпмүшелігін g көпмүшесіне қалдықпен болуге болады.
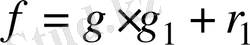 , мұндағы
, мұндағы
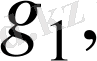
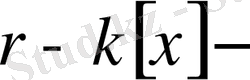 дегі көпмүшеліктер және
дегі көпмүшеліктер және
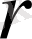
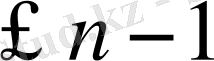 дәрежесінен. Сонда
дәрежесінен. Сонда
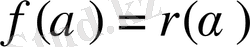 орындалады.
орындалады.
Сондықтан
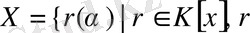 дәрежелі
дәрежелі
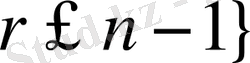 .
.
Бұдан шығатыны,
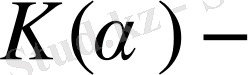 ғы кез келген К элементін
ғы кез келген К элементін
 түрінде көрсетеміз. Сондықтан
түрінде көрсетеміз. Сондықтан
 элементтерінің К өрісіне қолданылатын сызықтық комбинциялар барлық
элементтерінің К өрісіне қолданылатын сызықтық комбинциялар барлық
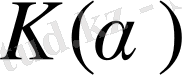 жиынын құрайды. Бұл элементтердің сызықтық тәуелсіз екендігіне көз жеткізейік. Егер олар сызықты тәуелді болса, онда
жиынын құрайды. Бұл элементтердің сызықтық тәуелсіз екендігіне көз жеткізейік. Егер олар сызықты тәуелді болса, онда
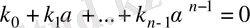 орындалатындай барлығы нөлге тең емес, К өрісінде
орындалатындай барлығы нөлге тең емес, К өрісінде
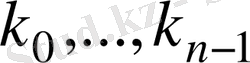 скалярлы (сандары) бар болады.
скалярлы (сандары) бар болады.
 саны К өрісіндегі осы көпмүшеліктің түбірі болып табылады. Сондықтан
саны К өрісіндегі осы көпмүшеліктің түбірі болып табылады. Сондықтан
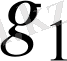 және
және
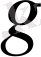 көпмүшеліктері
көпмүшеліктері
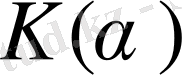 өрісінде
өрісінде
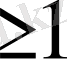 дәрежелі ең үлкен ортақ бөлгішке ие болады. Евклид алгоритмінің тамаша қасиеті бойынша бұл ең үлкен ортақ бөлгіш К өрісіндегі көпмшелік болып табылады. Сондықан
дәрежелі ең үлкен ортақ бөлгішке ие болады. Евклид алгоритмінің тамаша қасиеті бойынша бұл ең үлкен ортақ бөлгіш К өрісіндегі көпмшелік болып табылады. Сондықан
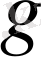 көпмүшелігі дәрежесі
көпмүшелігі дәрежесі
 ден
ден
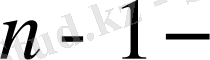 ге дейін болатын К өрісінде бөлгішке ие болады. Бұл осы өрістегі берілген көпмүшеліктің келтірілмейтіндігіне кері келеді.
ге дейін болатын К өрісінде бөлгішке ие болады. Бұл осы өрістегі берілген көпмүшеліктің келтірілмейтіндігіне кері келеді.
Сонымен
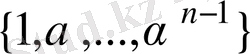 жиыны К скалярларының өрісіндегі
жиыны К скалярларының өрісіндегі
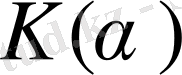 векторлық кеңістігінің базисі болып табылады. Демек,
векторлық кеңістігінің базисі болып табылады. Демек,
 дағы
дағы
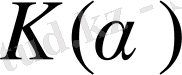 - ның өлшемі
- ның өлшемі
 ге тең болады.
ге тең болады.
в) Дәлелдеуді n бойынша индукция арқылы жүргіземіз. Егер
 болса, онда
болса, онда
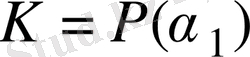 .
.
 нен кіші барлық натурал сандар үшін тұжырымдама дәлелденді деп ұйғарайық.
нен кіші барлық натурал сандар үшін тұжырымдама дәлелденді деп ұйғарайық.
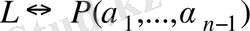 және
және
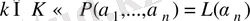 болсын.
болсын.
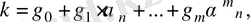 мұндағы
мұндағы
 орындалатындай
орындалатындай
 өрісінің коэффициенттерімен берілген
өрісінің коэффициенттерімен берілген
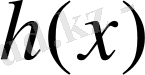 көпмүшелігі табылады.
көпмүшелігі табылады.
Индукция ұйғарымы бойынша
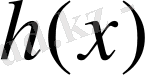 көпмүшелігінің барлық
көпмүшелігінің барлық
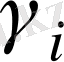 коэффициенттері
коэффициенттері
 айнымалыларына тәуелді Р өрсіндегі қандай да бір
айнымалыларына тәуелді Р өрсіндегі қандай да бір
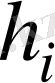 көпмүшеліктерінің
көпмүшеліктерінің
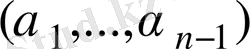 нүктесіндегі мәндеріне тең болады. Анықтама бойынша
нүктесіндегі мәндеріне тең болады. Анықтама бойынша

деп аламыз. Онда
 дан көпмүшелік және
дан көпмүшелік және
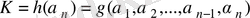 болады.
болады.
2) Р өрісіндегі n дәрежелі
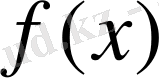 теңдеуі
теңдеуі
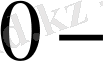 ге тең, яғни
ге тең, яғни
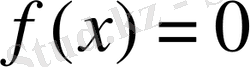 және
және
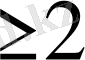 еселіктегі
еселіктегі
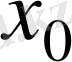 түбіріне ие болады деп ұйғарамыз. Онда бұл түбір
түбіріне ие болады деп ұйғарамыз. Онда бұл түбір
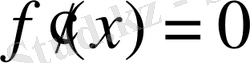 теңдеуінің де түбрі болып табылады. Оылайша,
теңдеуінің де түбрі болып табылады. Оылайша,
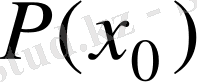 өрісіндегі
өрісіндегі
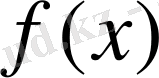 және
және
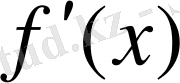 көпмүшеіктерінің ең үлкен ортақ
көпмүшеіктерінің ең үлкен ортақ
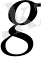 бөлгіші
бөлгіші
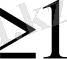 дрежесіне ие. Сонымен бірге
дрежесіне ие. Сонымен бірге
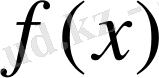 және
және
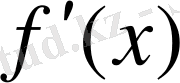 көпмүшеліктері Р өрісіндегі көпмүшеліктері болып табылады. Евклид алгоритмінің салдары
көпмүшеліктері Р өрісіндегі көпмүшеліктері болып табылады. Евклид алгоритмінің салдары
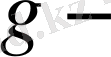 дің Р өрісіндегі көпмүшелік болып табылатындығы жөніндегі тұжырымдама болып табылады. Сондықтан
дің Р өрісіндегі көпмүшелік болып табылатындығы жөніндегі тұжырымдама болып табылады. Сондықтан
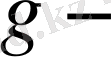 Р өрісіндегі
Р өрісіндегі
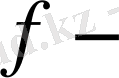 тің бөлгіші болып табыады.
тің бөлгіші болып табыады.
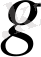 көпмүшелігінің дәрежесі, бір жағынан,
көпмүшелігінің дәрежесі, бір жағынан,
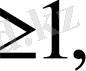 екінші жағынан
екінші жағынан
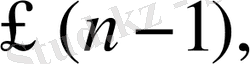 өйткені
өйткені
 көмүшелігінің де бөлгіші болып есептеледі. Бұл Р өрісіндегі
көмүшелігінің де бөлгіші болып есептеледі. Бұл Р өрісіндегі
 көпмүшелігінің келтірілмегендігі жөніндегі шартқа қарама - қайшы келеді.
көпмүшелігінің келтірілмегендігі жөніндегі шартқа қарама - қайшы келеді.
Кез келген алгебралық
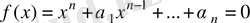 теңдеуі анық
теңдеуі анық
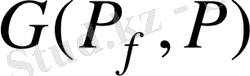 Галуа группасы Р өрісіндегі
Галуа группасы Р өрісіндегі
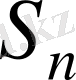 тобының ішкі тобына изоморфы болады.
тобының ішкі тобына изоморфы болады.
 көпмүшелігінің
көпмүшелігінің
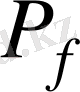 жктелу өрісін К арқылы белгілейміз, яғни
жктелу өрісін К арқылы белгілейміз, яғни
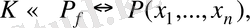 мұндағы
мұндағы
 бастапқы теңдеуінің барлық түбірлері. Әрине,
бастапқы теңдеуінің барлық түбірлері. Әрине,

Аталған маңызды ұйғарымды дәлелдеу үшін
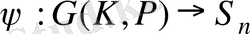 түріндегі инъективті гомоморфизмді анықтаймыз. Онда
түріндегі инъективті гомоморфизмді анықтаймыз. Онда
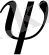
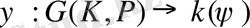 түріндегі изморфизм болып табылды және
түріндегі изморфизм болып табылды және
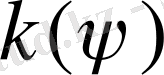
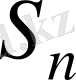 группасының ішкі группасы болып табылады.
группасының ішкі группасы болып табылады.
Алдымен
 көпмүшелігі Р да келтірілмеген, оның
көпмүшелігі Р да келтірілмеген, оның
 түбірлері әртүрлі болатын жағдайды қарастырамыз. Бұл жағдайда,
түбірлері әртүрлі болатын жағдайды қарастырамыз. Бұл жағдайда,
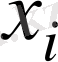 өзін немесе оның
өзін немесе оның
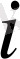 нөмерін жазу керек екендігі басты рольде емес, өйткені
нөмерін жазу керек екендігі басты рольде емес, өйткені
 түбірлері және олардың
түбірлері және олардың
 нөмірлері бекітілген биективті сәйкестікте болады.
нөмірлері бекітілген биективті сәйкестікте болады.
Сонымен,
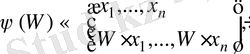 мұндағы
мұндағы
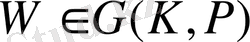 деп аламыз.
деп аламыз.
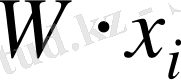 түріндегі сандар
түріндегі сандар
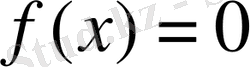 теңдеуінің түбірлері болып табылады, өйткені
теңдеуінің түбірлері болып табылады, өйткені
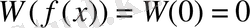 және
және
 яғни
яғни
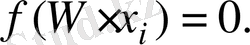 Мұндағы кез келген
Мұндағы кез келген
 элементі үшін
элементі үшін
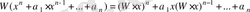 орындалатын факт қолданылады.
орындалатын факт қолданылады.
Егер
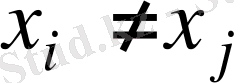 болса, онда
болса, онда
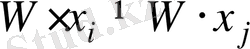 орындалады. Өйткені
орындалады. Өйткені
 инъективті функция болған. Сондықтан
инъективті функция болған. Сондықтан
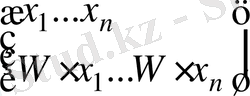 таблицасының төменгі қатарында әртүрлі
таблицасының төменгі қатарында әртүрлі
 сандары бар. Олардың барлығы
сандары бар. Олардың барлығы
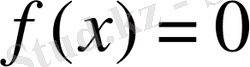 теңдеуінің түбірлері болып табылады, ол мұндай түбірлер
теңдеуінің түбірлері болып табылады, ол мұндай түбірлер
 нен көп емес. Сонымен, төменгі қатарда осы теңдеудің барлық
нен көп емес. Сонымен, төменгі қатарда осы теңдеудің барлық
 түбірлері жатады, яғни бұл таблица жоғарғы қатар биекциясын анықтайды. Сондықтан ол
түбірлері жатады, яғни бұл таблица жоғарғы қатар биекциясын анықтайды. Сондықтан ол
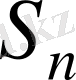 тобының элементі болып табылады, яғни
тобының элементі болып табылады, яғни
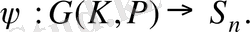
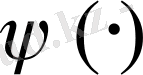 функциясы инъективті. Егер
функциясы инъективті. Егер
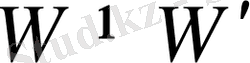 және
және
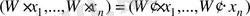 болса, онда К өрісінен кез келген
болса, онда К өрісінен кез келген
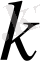 саны үшін келесі өрнек тбылады:
саны үшін келесі өрнек тбылады:
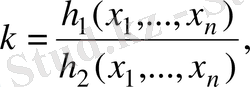 мұндағы
мұндағы
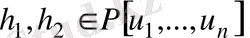
Онда
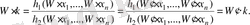
Қарама қайшылыққа келдік.
Тек
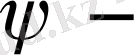 гомоморфизм екендігін тексеру ғана қалды.
гомоморфизм екендігін тексеру ғана қалды.
Шынына да,
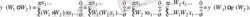 Егер
Егер
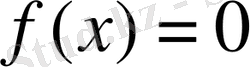 бастапқы теңдеуі келтірімейтін деп ұйғарылса, онда оның
бастапқы теңдеуі келтірімейтін деп ұйғарылса, онда оның
 түбірлерінің арасында тең болатындары болуы мүмкін.
түбірлерінің арасында тең болатындары болуы мүмкін.
Олардың ішінде жұп бойынша әртүрлі түбірлер
 , мұндағы
, мұндағы
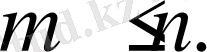 Онда
Онда
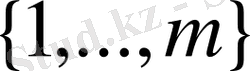 сандарының жиыны жұп бойынша әртүрлі
сандарының жиыны жұп бойынша әртүрлі
 түбірлерінің жиынымен биективті, және де
түбірлерінің жиынымен биективті, және де
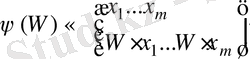 функиясы үшін жоғарыда айтылған талдаулар айтылады. Нәтижесінде
функиясы үшін жоғарыда айтылған талдаулар айтылады. Нәтижесінде
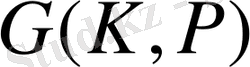 группасы
группасы
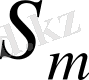 группасында, мұндағы
группасында, мұндағы
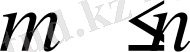 қосылады. Бірақ кез келген
қосылады. Бірақ кез келген
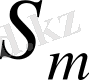 группасы
группасы
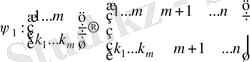 түрінегі инъективті гомоморфизм көмегімен
түрінегі инъективті гомоморфизм көмегімен
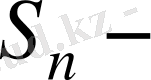 дегі ішкі топқа изоморфты болады.
дегі ішкі топқа изоморфты болады.
Сондықтан, еселік түбірлер жағдайында да
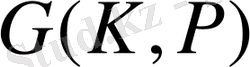 группасы да
группасы да
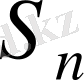 тобының ішкі группасына изоморфты болады.
тобының ішкі группасына изоморфты болады.
Галуа группасы, оның реті
Айталық К өрісі Р өрісінің кез келген нормальды өсімшесі болсын. К өсімшесі қарпайым алгебралық өсімше болып табылады, яғни К да мынадай
 элементі табылады
элементі табылады
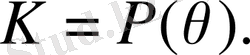
 элементінің
элементінің
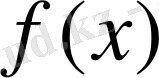 минимальды көпмүшенің дәрежесі Р өрісіндегі К өрісінің
минимальды көпмүшенің дәрежесі Р өрісіндегі К өрісінің
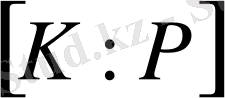 дәрежесіне тең. К өрісінің кез келген
дәрежесіне тең. К өрісінің кез келген
 элементі бірмәнді жазу түріне ие болады.
элементі бірмәнді жазу түріне ие болады.
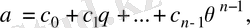
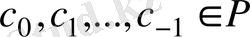

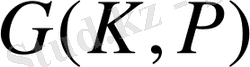 Галуа группасының кез келген
Галуа группасының кез келген
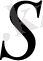 автоморфизмі
автоморфизмі
 түбірін қайтадан
түбірін қайтадан
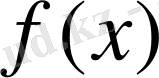 көпмүшесінің түбіріне ауыстырады. Басқа сөзбен айтқанда, әрбір
көпмүшесінің түбіріне ауыстырады. Басқа сөзбен айтқанда, әрбір
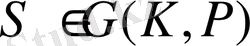 автоморфизмге
автоморфизмге
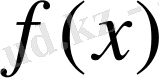 көпмүшенің кейбір түбірі сәйкес келеді. Осы сәйкестікті толық зерттейміз.
көпмүшенің кейбір түбірі сәйкес келеді. Осы сәйкестікті толық зерттейміз.
Айталық
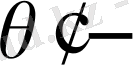 кез келген
кез келген
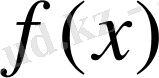 кез келген көпмүшенің түбірі болсын. К өрісі нормальды және
кез келген көпмүшенің түбірі болсын. К өрісі нормальды және
 болғандықтан, онда
болғандықтан, онда
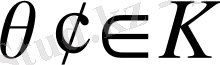 . К өрісіндегі
. К өрісіндегі
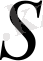 қайта құруын, осы өрістің кез келген
қайта құруын, осы өрістің кез келген
 элементті орнына қою арқылы анықтаймыз:
элементті орнына қою арқылы анықтаймыз:
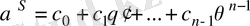
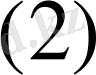
 элементінің жазылуы
элементінің жазылуы
 түрде бірмәнді, онда
түрде бірмәнді, онда
 формуланың
формуланың
 элементі бір ғана амалмен анықталады.
элементі бір ғана амалмен анықталады.
 түрлендірудің анықтамасын келесі түрде формула арқылы анықтауға болады: егер
түрлендірудің анықтамасын келесі түрде формула арқылы анықтауға болады: егер
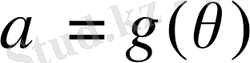
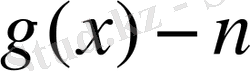 нен кіші дәрежесі бар Р өрісіндегі көпмүше болса, онда
нен кіші дәрежесі бар Р өрісіндегі көпмүше болса, онда
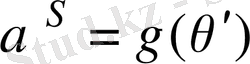
Енді Р өрісіндегі кез келген дәрежелі
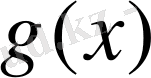 көпмүшесін қарастырайық және айталық
көпмүшесін қарастырайық және айталық
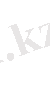
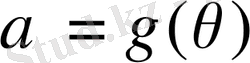
болсын.
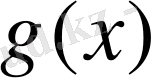 көпмүшесін
көпмүшесін
 көпмүшесіне (қалдықпен) бөлеміз:
көпмүшесіне (қалдықпен) бөлеміз:
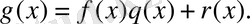 (3)
(3)
Бұл теңдіктен
 деп ұйғарып,
деп ұйғарып,
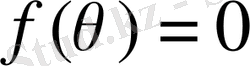 болғандықтан, біз мына теңдікті аламыз
болғандықтан, біз мына теңдікті аламыз
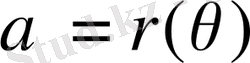
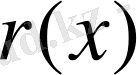 көпмүшенің дәрежесі
көпмүшенің дәрежесі
 нен кіші болғандықтан, онда бұдан шығады:
нен кіші болғандықтан, онда бұдан шығады:

Басқаша жағдайда,
 формуладан
формуладан
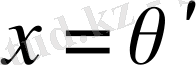 деп ұйғарып, келесіні аламыз
деп ұйғарып, келесіні аламыз
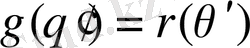 .
.
Демек,
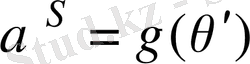
Сонымен,
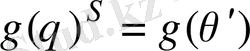
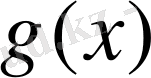 көпмүшесінің дәрежесіне байланыссыз.
көпмүшесінің дәрежесіне байланыссыз.
Айталық
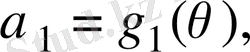
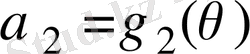
- К өрісінің кез келген элементі болсын. Сонда
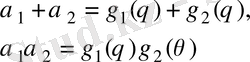
және, олай болса,
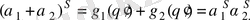
Сонымен,
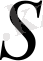 түрлендіруі қосынды мен көбейтіндіні сақтайды, яғни
түрлендіруі қосынды мен көбейтіндіні сақтайды, яғни
 шартына ие болады. Бұл түрлендіру Р өрісінің барлық элементтерін орнына қалдырады. Сондықтан
шартына ие болады. Бұл түрлендіру Р өрісінің барлық элементтерін орнына қалдырады. Сондықтан
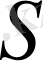 түрлендіруі Р өрісіндегі К өрісінің автоморфизмі болып табылады, яғни
түрлендіруі Р өрісіндегі К өрісінің автоморфизмі болып табылады, яғни
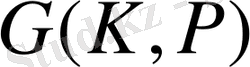 Галуа группасына жатады.
Галуа группасына жатады.
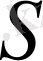 түрлендіруі автоморфизм болып табылады, яғни
түрлендіруі автоморфизм болып табылады, яғни
 шарттан тыс өзара бірмәнді қасиетін дәлелдеу мүмкіндігі шындық. Шынында да,
шарттан тыс өзара бірмәнді қасиетін дәлелдеу мүмкіндігі шындық. Шынында да,
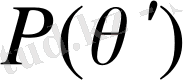 өрісін қарастырайық.
өрісін қарастырайық.
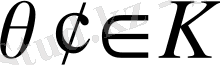 болғандықтан, онда
болғандықтан, онда

Басқаша жағдайда, Р өрісіндегі
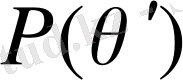 өрісінің дәрежесі
өрісінің дәрежесі
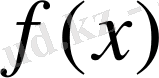 көпмүшесінің дәрежесіне тең, яғни К өрісінің дәрежесіне тең. Демек,
көпмүшесінің дәрежесіне тең, яғни К өрісінің дәрежесіне тең. Демек,
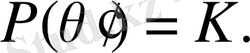
Бұдан,
 жазуымен қатар К өрісінің кез келген
жазуымен қатар К өрісінің кез келген
 элементі мағыналас түрде жазылатыны шығады
элементі мағыналас түрде жазылатыны шығады
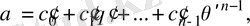

мұндағы
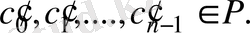
Енді К өрісінің
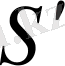 түрлендіруі өзгерту функциясын, осы өрісте әрқандай элементке
түрлендіруі өзгерту функциясын, осы өрісте әрқандай элементке
 қою арқылы анықтаймыз
қою арқылы анықтаймыз
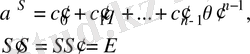
болғандықтан, онда
 түрлендіруі К өрісіндегі мәндес түрлендіруі болып табылады.
түрлендіруі К өрісіндегі мәндес түрлендіруі болып табылады.
S автоморфизмінен құрылған
 түбірі
түбірі
 түбіріне ауысады:
түбіріне ауысады:
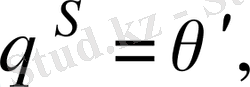
яғни жоғары мағынада көрсетілген бұл автоморфизм
 түбіріне сәйкес келеді. Сонымен, кез келген
түбіріне сәйкес келеді. Сонымен, кез келген
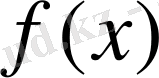 көпмүшесінің түбірі үшін
көпмүшесінің түбірі үшін
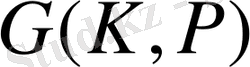 Галуа группасында осы түбірге сәйкес келетін автоморфизмнің табылатыны дәлелденді. Түбірмен сәйкес келетін автоморфизм бірмәнді анықталады, яғни егер
Галуа группасында осы түбірге сәйкес келетін автоморфизмнің табылатыны дәлелденді. Түбірмен сәйкес келетін автоморфизм бірмәнді анықталады, яғни егер
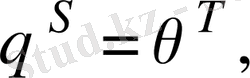
онда

Шынында да, егер
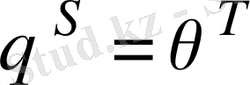 болса, онда
болса, онда
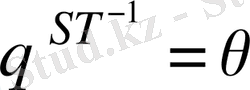 болады, яғни
болады, яғни
 автоморфизмі
автоморфизмі
 түбірін орнында қалдырады және олай болса, төмендегі кез келген түрді орнында қалдырады
түбірін орнында қалдырады және олай болса, төмендегі кез келген түрді орнында қалдырады
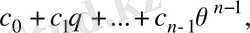 мұндағы
мұндағы
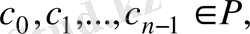
яғни К өрісінің кез келген элементін орнында қалдырады. Сөйтіп,
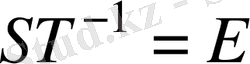 және
және

Сонымен,
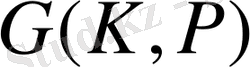 Галуа группасының элементтері (яғни Р өрісіндегі К өрісінің автоморфизмдері)
Галуа группасының элементтері (яғни Р өрісіндегі К өрісінің автоморфизмдері)
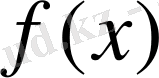 көпмүшенің түбірлерімен сәйкес келетін өзара бірмәнді және олай болса, олардың сандары, яғни
көпмүшенің түбірлерімен сәйкес келетін өзара бірмәнді және олай болса, олардың сандары, яғни
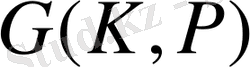 группасының реті
группасының реті
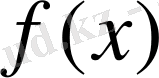 көпмүшенің түбірінің санына тең, яғни n- ге тең (бұл көпмүше келтірілмеген болғандықтан, барлық
көпмүшенің түбірінің санына тең, яғни n- ге тең (бұл көпмүше келтірілмеген болғандықтан, барлық
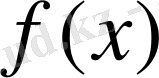 көпмүшенің түбірлері әр түрлі) . Сонымен біз,
көпмүшенің түбірлері әр түрлі) . Сонымен біз,
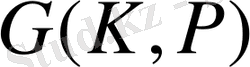 Галуа группасының реті Р өрісіндегі К өрісінің дәрежесіне тең екенін дәлелдедік.
Галуа группасының реті Р өрісіндегі К өрісінің дәрежесіне тең екенін дәлелдедік.
Галуа сәйкестігі
Айталық,
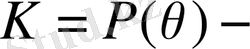 кез келген негізгі Р өрісінің нормальды өсімшесі және
кез келген негізгі Р өрісінің нормальды өсімшесі және
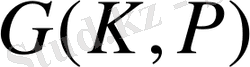 оның Р өрісіндегі Галуа группасы болсын.
оның Р өрісіндегі Галуа группасы болсын.
К өрісіндегі Р өрісінің
 ішкі өсімшесін қарастырамыз:
ішкі өсімшесін қарастырамыз:
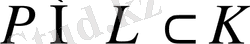 .
.
Мұндай өсімшелерді біз аралық өрістер деп атаймыз.
 саны түбірі болып табылатын, Р өрісіндегі
саны түбірі болып табылатын, Р өрісіндегі
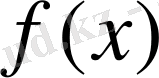 көпмүшесін және әрқандай
көпмүшесін және әрқандай
 аралық өрісінің көпмүшесін қарастыруға болады. Оның
аралық өрісінің көпмүшесін қарастыруға болады. Оның
 дегі жіктелу өрісі
дегі жіктелу өрісі
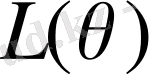 өрісі болып табылады. Демек,
өрісі болып табылады. Демек,
 өрісіндегі
өрісіндегі
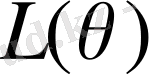 өрісі нормальды. Басқаша жағдайда,
өрісі нормальды. Басқаша жағдайда,
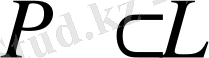 болса, онда
болса, онда
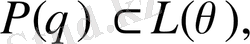 яғни
яғни
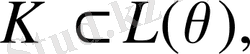 ал
ал
 және
және
 болса, онда
болса, онда
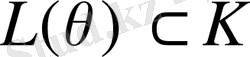 болады. Демек,
болады. Демек,

К өрісі әрқандай аралық
 өрісінде нормальды.
өрісінде нормальды.
Сондықтан
 өрісіндегі К өрісінің
өрісіндегі К өрісінің
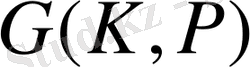 Галуа группасы туралы сөйлеуге болады.
Галуа группасы туралы сөйлеуге болады.
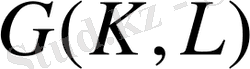 группасының реті
группасының реті
 өрісіндегі К өрісінің дәрежесіне тең.
өрісіндегі К өрісінің дәрежесіне тең.
Анықтама бойынша,
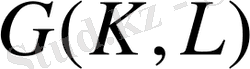 группаның элементтері, әрқандай
группаның элементтері, әрқандай
 өрісінің элементтерін орнында қалдыратын К өрісінің автоморфизмдері болып табылады.
өрісінің элементтерін орнында қалдыратын К өрісінің автоморфизмдері болып табылады.
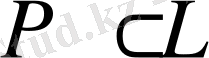 болса, онда бұл автоморфизмдер кез келген Р өрісінің элементтерін орнында қалдырады, яғни Р өрісіндегі К өрісінің
болса, онда бұл автоморфизмдер кез келген Р өрісінің элементтерін орнында қалдырады, яғни Р өрісіндегі К өрісінің
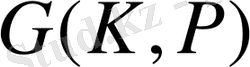 Галуа группасының элементтері болып табылады. Сөйтіп,
Галуа группасының элементтері болып табылады. Сөйтіп,
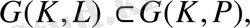
яғни,
 өрісіндегі К өрісінің Галуа группасы Р өрісіндегі К өрісінің Галуа группасының ішкі группасы болады. Оның реті
өрісіндегі К өрісінің Галуа группасы Р өрісіндегі К өрісінің Галуа группасының ішкі группасы болады. Оның реті
 өрісіндегі К өрісінің
өрісіндегі К өрісінің
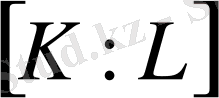 дәрежесіне тең.
дәрежесіне тең.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz