Стереометрия

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

13-ТАРАУ. СТЕРЕОМЕТРИЯ

§ 1. КЕҢІСТІКТЕГІ ТҮЗУЛЕР МЕН ЖАЗЫҚТЫҚТАР

1. 1. Параллель түзу мен жазықтық

Параллельдік белгісі:

▪Егер b түзі a жазықтығында жатқан қандай да бір a түзуіне параллель болса, онда b түзуі a жазықтығына да параллель болады: a $\ \$ b, a $\in \alpha \Rightarrow b\ \\ a$ .

b

Aaaa a

$▪$ Егер бір жазықтықта жататын қиылысқан екі түзудің әрқайсысы екінші жазықтыққа параллель болса, онда жзықтықтар параллель болады.

1. 2 Түзу мен жазықтықтың перпендикулярлығы

Егер жазықтықпен қиылысатын түзу жазықтықта жатқан кез келген түзуге қиылысу нүктесінде перпендикуляр болса, онда берілген түзу жазықтыққа перпендикуляр болады : ( b, c $\ \in \alpha$ ) a ┴ b, a ┴ c ⇒ a ┴ $\alpha$ .

1. 3 Перпендикуляр жазықтықтар

Егер бір жазықтықта екінші жазықтыққа перпендикуляр түзу жатса, онда екі жазықтық перпендикуляр болады:

(a $\ \in \alpha) \$ a ┴ $\beta$ ⇒ $\alpha$ ┴ $\beta$ .

1. 4 Перпендикуляр және көлбеу

▪ Перпендикуляр кесінді, жазықтыққа бір нүктеден жүргізілген кез келген көлбеуден қысқа.

▪ Жазықтыққа бір нүктеден жүргізілген тең көлбеулердің проекциялары да тең.

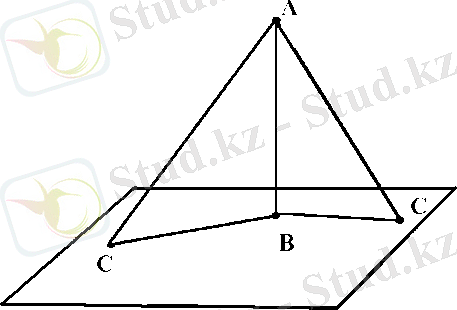
3. 1 Көпжақтар

Кеністікте жазык копбұрыштармен шектелген денеге көпжақ дейміз. Әр көпбұрыш онын жағы, жақтарынын кабырғалары көпжактың қырлары, ал жактардыңтөбелері онын төбелері деп аталады. Жақтар көпжақтың бетін кұрайды. Бір жазықтыкта жатпайтын скі төбені косатын кесіндіні көпжактың диагоналі деп атайды.

Айталык т - көпжакгын жақтар саны , п - төбелер саны, ал р - оның кырлар саны болсын.

Олай болса, кез келген көпжақ үшін келесі катынас орындалады: п + т - р = 2 (Эйлер теоремасы) .

Егер барлык жақтары дұрыс көпбұрыш, ал барлык төбелеріндегі көпжакты бұрыштар өзара тең болса, ондай көпжак дұрыс көпжақ деп аталады.

Барлык жактары тенкабырғалы үшбұрыш болатын дұрыс төртжақка дұрыс тетраэдр дейміз.

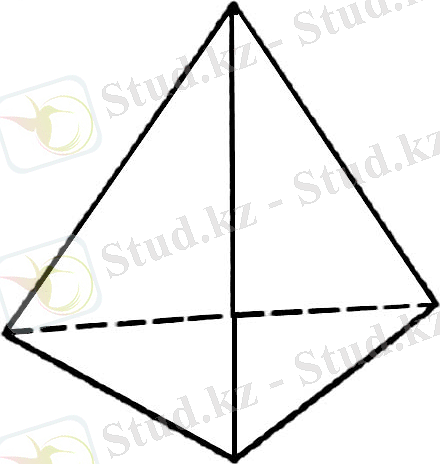
Дұрыс алтыжақ- куб.

3. 2. Призма. Параллелепипед. Куб

Екі жағы параллель жазықтықтарда орналасқан өзара тең көпбұрыштар, ал қалған жақтары параллелограмм болып келген көпжақты призма деп атайды. Параллель жазықтықтарда жатқан тең көпбұрыштар оның табандары деп, ал қалған параллелограмдар оның бүйір жақтары деп аталады.

Егер призманың бүйір қырлары табанарына перпендикуляр болса, призманы тік , қалған жағдайда көлбеу деп атаймыз.

көлбеу призма тік призма

Табандары дұрыс көпбұрыш болып келетін ітік призма дұрыс призма деп аталады.

Призманың бүйір бетінің ауданы деп оның бүйір жақтарының аудандарының қосындысын айтады.

Призманың бетінің ауданы мен көлемі

Көлбеу призма

Тік призма

: Бүйір бетінің ауданы

Көлбеу призма:

S _{б. б} = P _{┴

٠} L,

Мұндағы P _┴ -перпендикуляр қиманың периметрі, L-бүйір қыры

Тік призма:

S _{б. б} =P _{таб

٠} H,

Мұндағы P _таб - табанының периметрі, H - биіктік.

: Толық бетінің ауданы

Көлбеу призма: S _{т. б} =S _{б. б} + 2 S _таб

Тік призма: S _{т. б} =S _{б. б} + 2 S _таб

: Көлемі

Көлбеу призма:

V = S _┴ ٠ L,

Мұндағы S _┴ - перпендикуляр қиманың ауданы, L - бүйір қыры

Тік призма:

V = S _таб ٠ Н,

МұндағыS _таб -табан ауданы, H -биіктік.

1-мысал: Үшбұрышты көлбеу призманың бүйір қырлары бір-бірінен 13, 14 және 15 см қашықтықта орналасқан, бүйір қырының ұзындығы 5 см. Призманың бүйір бетінің ауданы мен көлемін табыңыз:

Шешуі: Бүйір бетінің ауданын келесі формуламен табамыз: S _{б. б =} P _┴ ٠ L

P _{┴ =} 13 + 14 +15 = 42 см, L = 5 см.

Олай болса, S _{б. б =} 210см ² . Призманың көлемін табу үшін V = S _┴ ٠ L формуласын қолданайық. Герон формуласы бойынша

S _┴ = $\ \sqrt{}$ 21 ٠8 $٠$ 7 ٠ 6 = 84см ²

Сонымен, V = 84 ٠ 5 = 420см ²

Жауабы: 420см ²

2-мысал: Тік призманың табаны сырттай сызылған шеңберінің радиусы 2 $\sqrt{}3$ болатын теңқабырғалы үшбұрыш. Егер призма биіктігі 4-ке тең болса, оның бүйір бетінің ауданы мен көлемін табыңыз.

Шешуі: Табанының қабырасы: a = R $\sqrt{3}$ (теңқабырғалы үшбұрыш қасиеті), яғни a = 2 $\sqrt{}3$ ٠ $\sqrt{}3$ = 6 . Үшбұрыш периметрі P = 18, онда S _{б. б} = 72.

S _таб = $\frac{\alpha ²\sqrt{3}}{4}$ = $\frac{36\sqrt{3}}{4}$ =9 $\sqrt{}3$

Көлемі келесі формула арқылы анықталады: V = S _таб _٠ H V = S _таб _٠ H =9 $\sqrt{3٠4} = 36\sqrt{}3$

Жауабы: S _{б. б} = 72 және V = 36 $\sqrt{}3$ .

Параллелепипед

Табаны параллелограмм болып келетін призма параллелепипед деп аталады.

Параллелепипедтің бір нүктеде қиылысатын жәнеқиылысу нүктесінде қақ бқлінетін 4 диагоналі бар.

Параллелепипед призманың дербес жағдайы болғандықтан, призманың бүйір бетінің ауданы мен көлемін табу формулалары ол үшін де дұрыс.

d1²+d2²+d3²=4α²+4b²+4c²

Тік параллелепипед

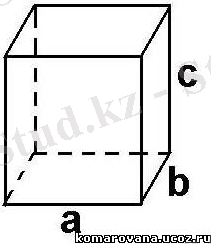
Бүйір қырлары табандарына перпендикуляр.

Бүйір жақтары - тіктөртбұрыштар.
Табандары - параллелограмм.

Тіктөртбұрышты параллелепипед

Табаны тіктөртбұрыш болып табылатын тік параллелепипед тіктөртбұрышты деп аталады.

Барлық диагоналдары өзара тең
d2= a2+ b2+ c2
Sт. б= 2(ab + ac +bc)
V = abc

3-мысал: Көлбеу параллелепипедтің табанында бұрышы 30 ⁰ - қа, қабырғасы 5-ке тең ромб жатыр. Бүйір қыр $\ \ \frac{4}{\sqrt{3}}$ және табан жазықтығына 60 ⁰ көлбеген. Параллелепипед көлемін табыңыз.

Шешуі: Параллелепипед көлемі:

V = S _таб _٠ H

Сүйір бұрышы 30 ⁰ және қабырғасы 5-ке тең ромб болатын табанының ауданы

S _таб = 5 ٠ 5 ٠ sin30 ⁰ = $\frac{25}{2}$

∆AFA᾿ үшбұрышынан биіктігін табамыз: sin 60 ⁰ = $\frac{A'F}{AA'}$ ⇒ $\frac{\sqrt{3}}{2}$ = $\frac{A'F}{\frac{4}{\sqrt{3}}}$ ⇒A'F=2

Олай болса, V = S _таб _٠ A'F = $\frac{25}{2}$ ⋅2=25

Жауабы: 25.

4-мысал: Тік параллелепипедтің табан қабырғалары 8 және 4, 60 ⁰ бұрыш жасайды. Параллелепипедтің кіші диагоналі 8 $\sqrt{3} - ке$ тең. Осы диагональдың табанымен жасайтын бұрышты табыңыз.

Шешуі: 1) Табанының кіші диагоналін тауып аламыз: BD:

∆ABD: BD ² = 8 ² +

4 ² - 2 ٠ 4 ٠ 8 cos 60 ⁰ ⇒

BD= $\sqrt{64} + 16 - 32$ = $\sqrt{48} = 4\sqrt{3}$

(косинустар теоремасы)

2) ∆ BDD’:

cos∠DBD’ = $\frac{BD}{BD'}$ ⇒cos ∠DBD'= $\frac{4\sqrt{3}}{8\sqrt{3}}$ = $\frac{1}{2}$

3) ∠DBD’ = 60 ⁰ .

Жауабы: 60 ⁰ .

Куб

Барлық жақтары квадрат тікбұрышты параллелепипед куб деп талады.

Кубтың толық бетінің ауданы Sт. б= 6a2, мұндағыa -қырының ұзындығы.
Кубтың диагоналіd =a3\sqrt{3}
Кубтың көлемі:V= a

5-мысал: Кубтың диагональ қимасының ауданы 8 $\sqrt{}$ 2 -ге тең. Кубтың толық бетінің ауданын табыңыз.

Шешуі:

Көмекші элемент енгізейік : a- кубтың қыры.

∆ ABC : AC = a $\sqrt{}2$ .

Қиманың ауданы: S _қима = a ٠ a $\sqrt{2} =$ 8 $\sqrt{}2$ ⇒ a = 2 $\sqrt{}2$

Толық бетінің ауданы: S _{т. б} = 6a ² = 6 ٠ ( 2 $\sqrt{}2$ ) ² = 48

Жауабы:48.

4. 2. Конус. Қиық конус

Конус дегеніміз - дөңгелектен ( конустың табаны ) , дөңгелек жазықтығында жатпайтын нүктеден (конустың төбесі) және нүкте мен дөңгелекті біріктіруші кесінділерден тұратын геометриялық дене. Конустың төбесін табанындағы шеңбердің нүктелерімен біріктіретін кесінділер конустың жасаушылары деп аталады.

Егер конустың төбесі мен табанының центрінен өтетін түзу табанына перпендикуляр болса, онда конусты тік конус дейміз. Енді біз тек тік коністарды қарастыратын боламыз және қысқаша конус деп атаймыз.

Конус ішіндегі ABC теңбүйірлі үшбұрыш конустың осьтік қимасы деп аталады.

Конустың табаны мен табанына параллель қимамен шектелген бөлігі қиық конус деп аталады.

Конустың бетінің ауданы мен көлемі

Конус

Қиық конус

: Бүйір бетінің ауданы

Конус: S _{б. б} =

\pi RL

Қиық конус: S _{б. б} =

\pi(

R + r) L, мұндағы L -қиық конустың жасаушысы

: Толық бетінің ауданы

Конус: S _{т. б} =

\pi

R(R+L)

Қиық конус: S _{т. б} =

\pi

(R + r) L +

\pi

R ² +

\ \pi

r ²

: Көлемі

Конус:

V= $\frac{1}{3}\pi$ R²H

Қиық конус:

V= $\frac{1}{3}\pi$ h(R²+Rr+r²) = $\frac{h}{3}$ (S₁+S₂+ $\sqrt{S₁S₂}$ )

Мұндағы S1, S2 - табандарының ауданы

Бүйір бетінің жазбасының (сектордың бұрышы) α= $\frac{\mathbf{2\pi R}}{\mathbf{l}}$ формуласымен табылады.

3-мысал: Конустың бүйір бетінің ауданы табанының ауданынан екі есе үлкен. Егер осьтік қимасы 3 $\sqrt{}3$ болса, конустың көлемін есептеңіз.

Шешуі: Есептің шарты бойынша, S _{б. б} = 2S _таб , яғни $\pi RL\$ = 2 $\pi R$ ² , осыдан L= 2R, демек, ∆ ABC - теңқабырғалы.

S _∆ABC = $\frac{l²\sqrt{3}}{4}$ =R² $\sqrt{3}$

R ² $\sqrt{3}$ = 3 $\sqrt{}3$ ⇒ R = $\sqrt{}3$ , H = R $\sqrt{}3$ = 3.

V= $\frac{1}{3}\pi$ R²H= $\frac{1}{3}\pi$ ( $\sqrt{3}$ ) ²⋅3=3 $\pi$ .

Жауабы : 3 $\pi$ .

4-мысал: Конустың биіктігі 4, ал осьтік қимасының төбесіндегі бұрыш 90 ⁰ -қа тең. Конустың бүйір бетінің ауданын табыңыз.

Шешуі: Берілген бойынша ∠ ACB = 90 ⁰ .

Сонымен қатар тік бұрыштан жүргізілген медиана гипотенузаның жартысы болатыны белгілі 4= $\frac{AB}{2}$ ⇒4=R

жасушысы: L = $\sqrt{4² - 4²}$ = 4 $\sqrt{}2$

Олай болса , S _{б. б} = $\pi RL = \ \pi$ ٠ 4 ٠ 4 $\sqrt{2}$ = 16 $\sqrt{}2\pi$

Жауабы: 16 $\sqrt{}2\pi$ .

5-мысал: Қиық конустың табандарының радиусы 1 және 9, ал жасаушысы 10-ға тең. Көлемін табыңыз.

Шешуі: ОО ₁ биіктігін NC-ге параллель көшірейік. Онда AN = AO -NO = 9 -1 = 8.

∆NC : CN = $\sqrt{10² - 8²}$ = 6 . Сонымен, V= $\frac{1}{3}\pi$ h(R²+Rr+r²) = $\frac{1}{3}\ \pi$ ⋅6⋅(9²+9+1²) =182 $\pi$

Жауабы: 182 $\pi$

6-мысал: Табандары 13 және 18, ал кіші бүйір қабырғасы 12-ге тең тік трапецияны айналдырғаднда шыққан қиық конустың толық бетінің ауданын табыңыз.

Шешуі: AD биіктігін CN -ге параллель көшірейік, онда BN = AB - AN = 18 -13 = 5

∆BNC : L = BN = $\sqrt{}$ 12 ² + 5 ² = 13.

S _{т. б} = $\pi$ (R + r) L + $\pi$ R ² + $\pi r$ ²

S _{т. б} = $\pi$ (18 + 13) ٠ 13 + 18 ² $\pi\$ + 13 ² $\pi$ = 896 $\pi$ .

Жауабы: 896 $\pi$

4. 3. Шар. Сфера

Сфера дегеніміз - берілген О ( центр ) нүктесінен бірдей R ( радиус ) қашықтықта орналасқан нүктелердің геометриялық орны. Шар деп центрден қашықтығы радиус ұзындығынан аспайтын нүктелердің геометриялық орнын айтамыз.

Сфераның радиусы жанама жазықтыққа жанасу нүктесінде перпендикуляр болады.
Шардың кез келген қимасы дөңгелек болады және бұл дөңгелектің центрі шардың центрінен қиюшы жазықтыққа түсірілген перпендикулярдың табаны болып табылады. Шардың диаметрі арқылы өтетін қима үлкен дөңгелек, ал сфераны қиып өтсе - үлкен шеңбер деп аталады.
Егер қиманың жазықтығы шардың центрінен қашықтықта орналасса, ондаr=R2+d2\sqrt{R^{2} + d^{2}}мұндағыr- қиманың радиусы.

СУРЕТ

Сфераның ауданы: S=4πR ²

Шардың көлемі:V= $\frac{4}{3}$ πR ³

Шардың бөліктері

СУРЕТ

шар сегменті шар секторы шар қабаты

Сегмент бетінің ауданы:

S _сегм =2πRH

Сектордың толық бетінің ауданы:

S _{m. б} = $\pi$ R(2H+ $\sqrt{2RH}{- H}^{2}$ )

Шар қабатының бетінің ауданы:

$S_{бет}$ =2π RH

Сегмент бетінің ауданы:Sсегм=2πRH:

Сегмент көлемі:

V= $\frac{1}{3}\pi H^{2}$ (3R-H)

Сектордың толық бетінің ауданы:Sm. б=π\piR(2H+2RH−H2\sqrt{2RH}{- H}^{2}):

Сектордың көлемі:

V= $\frac{2}{3}\pi R^{2}$ H

Шар қабатының бетінің ауданы:SбетS_{бет}=2πRH:

Көлемі:

V= $\frac{1}{6}$ π $H^{3}$ + $\frac{1}{2}$ ( $r_{1}^{2}{+ r}_{2}^{2}$ ) H

7-мысал: Іші қуыс шардың сыртқы диаметрі

20. Қабырғасының қалыңдығы 4. Шар жасалған материалдың көлемін табыңыз.

СУРЕТ

Шешуі: Іші қуыс шардың центрінен қима жүргізіп қарастырайық. Алынған қима сақина болады.

ОВ= ОА-АВ= 10-4=6

$V_{1}$ - $V_{2}$ = $\frac{4}{3}$ π ( ${OA}^{3} - {OB}^{3}$ ) = $\ \frac{4}{3}$ π ( $10^{3} - 6^{3}$ ) = $\frac{4 \bullet 784}{3}\$ $\pi = \frac{3136}{3}$ π

Жауабы : $\frac{3136}{3}$ π

8-мысал: Шардың центрінен бір жағынан екі параллель қима жүргізілген. Қималардың арақашықтығы 3. Егер қималардың радиустары 9 және 12 болса, шардығ көлемін анықтаңыз.

СУРЕТ

Шешуі: Көмекші элемент енгізейік:

${ОО}_{1}$ =х

ΔОО1В:ОВ\mathrm{\Delta}{ОО}_{1}В:ОВ=ОО12\sqrt{{ОО}_{1}^{2}}+О1В2О_{1}В^{2}=х2122\sqrt{х^{2}}12^{2}

$\mathrm{\Delta}{ОО}_{2}А:ОА$ = $\sqrt{{ОО}_{2}^{2}}$ + $О_{2}А^{2}$ = $\sqrt{({х + 3) }^{2} +}9^{2}$

ОВ=ОА=R болғандықтан

$\sqrt{х^{2}}12^{2}$ = $\sqrt{({х + 3) }^{2} +}9^{2}$

$x^{2} + 144 = x^{2} + 6x$ +90

6x=54

x=9

Яғни ${ОО}_{1}$ =9

$ОВ = \sqrt{{ОО}_{1}^{2}} +$ + $О_{1}В^{2}$ = $\sqrt{х^{2}}12^{2}$ = $\sqrt{81 + 144 = 15}$

V=43πR3\frac{4}{3}\pi R^{3}=43\frac{4}{3}π•153\bullet 15^{3}=4500π

Жауабы: 4500π

$§$ 5. КӨПЖАҚТАР МЕН АЙНАЛУ ФИГУРАЛАРЫНЫҢ КОМБИНАЦИЯЛАРЫ

Призма мен цилиндр

Цилиндрге іштей сызылған призмадеп табандары цилиндрдің табандарына іштей сызылған призманы айтады. Призманың бүйір қырлары цилиндрдің жасаушыларымен беттеседі.
Цилиндрге сырттай сызылған призмадеп табандары цилиндрдің табандарына сырттай сызылған призманы айтады. Цилиндрге сырттай сызылған кез келген призманың биіктігі сол цилиндрдің биіктігіне тең.

1-мысал: Цилиндрге іштей дұрыс үшбұрышты призма сызылған. Призманың табан қабырғасы $\alpha$ , ал бүйір қыры - b . Цилиндрдің бүйір бетінің ауданын және көлемін анықтаңыз.

СУРЕТ

Шешуі: Призманың табаны - дұрыс ұшбұрыш.

Цилиндрдің радиусы үшбұрышқа сырттай сызылған шеңбердіңрадиусымен беттеседі және ұзындығы $\frac{\bullet \alpha\sqrt{3}}{3}$ -ға тең (тең қабырғалы үшбұрыш қасиетінен), ал цилиндрдің биіктігі - b.

Онда, бүйір бетінің ауданы:

$S_{6. 6. }$ = 2π $\frac{\bullet \alpha\sqrt{3}}{3}$ b= $\frac{2\pi}{\sqrt{3}}$ $\alpha b$

Цилиндрдің көлемі:

V=π $R^{2}$ H= $\pi\left( \frac{\alpha\sqrt{3^{2}}}{3} \right) \bullet$ b= $\frac{\alpha^{2}b}{3}$ π

Жауабы: $\ \frac{2\pi}{\sqrt{3}}$ $\alpha b;$ $\frac{\alpha^{2}b}{3}$ π.

Пирамида мен конус

Конусқа іштей сызылған пирамидадеп табаны конустың табанына іштей сызылған, ал төбесі конусың төбесімен беттесетін пирамиданы айтады. Іштей сызылған пирамиданың бүйір қырлары конустың жасушаларымен беттеседі.
Конусқа сырттай сызылған пирамидадеп табаны конустың табанына сырттай сызылған, ал төбесі конустың төбесімен беттесетін пирамиданы бүйір жақтары конустың бүйір бетін жанайды.

2- мысал: Конусқа іштей тік пирамида сызылған. Пирамида табаны-қабырғалары $\alpha$ және $b$ болатын тіктөртбұрыш. Пирамида және конус көлемдерінің қатынасын табыңыз.

СУРЕТ

Шешуі: Тіктөртбұрыш диагоналі сырттай сызылған шеңбердің диаметріне тең.

диаметр = 2R= $\sqrt{\alpha^{2} + b^{2}}$ $= >$ R = $\frac{\sqrt{\alpha^{2} + b^{2}}}{2}$

V _конус = $\frac{1}{3}\pi$ ( $\sqrt{\alpha^{2}{+ b}^{2}}$ ) ² H= $\frac{1}{3}$ π ( $\alpha^{2}{+ b}^{2}$ ) H және V _{пирамида} = $\frac{1}{3}$ $\alpha bH$