Кездейсоқ шамалардың сандық сипаттамалары: математикалық күтім және оның қасиеттері


Қ. А. Ясауи атындағы халықаралық Қазақ - Түрік университеті
Жаратылыстану және медицина институты
Математика кафедрасы
Тақырыбы : Кездейсоқ шамалардың сандық сипаттамлары
Түркістан - 2008
Жоспар
- Кездейсоқ шамалардың сандық сипаттамлары
туралы түсінік.
- Математикалық күтім.
- Математикалық күтімнің қасиеттері.
Пайдаланылған әдебиеттер.
- Қ. Бектаев «Ықтималдықтар теориясы және
математикалық статистика»
Алматы «Рауан» 1991 ж.
- В. Е. «Руководство к решению задач
по теории вероятностей и математической статистике»
Москва «Высшая школа» 2003 г.
Көптеген практикалық мәселелерді шешкенде кездейсоқ шаманың үлестіру заңын іздестірмей - ақ оны, анықтау кейде қиынға да соғады, сол үлестірудің маңызды ерекшелігін қамтитын кейбір сандық сипаттамаларын (характеристикалармен) қанағаттануға болады.
Ықтималдықтар теориясында бұл сандық сипаттамалар мен оларға қолданылатын операциялардың рөлі өте-өте зор. Осы сандық сипаттамаларды білу нәтижесінде көптеген ықтималдықтар есептерін шешу жеңілденеді, әрине, мұндай сандық сипаттамлар көп -ақ. Біз солардың ішінен математикалық күтім, оның қасиеттерін қарастырамыз.
Анықтама. Дискретті кездейсоқ Х - тің математикалық күтімі деп оның барлық мүмкін мәндерін сәйкес ықтималдықтарына көбейтілген қосындысын айтамыз.
Кездейсоқ шама Х - тің математикалық күтімін МХ арқылы белгілесек, онда
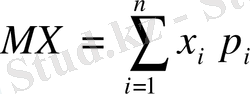
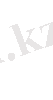 (1)
(1)
деп жазамыз. Әрине,
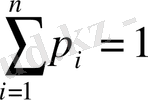 (2)
(2)
Ал егер
Х
саналымды шексіз
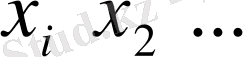 мәндерін сәйкес
мәндерін сәйкес
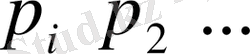 ықтималдықтарымен қабылдаса және
ықтималдықтарымен қабылдаса және
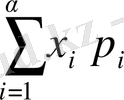 қатары абсолютті жинақты болса, онда
қатары абсолютті жинақты болса, онда
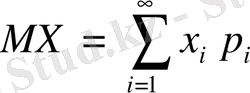 (1’)
(1’)
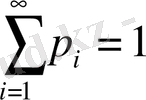 (2’)
(2’)
болады. Ал
Х
үздіксіз кездейсоқ шама болса, онда
Х -
тің қабылдаған
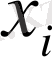 дербес мәндерін үздіксіз өзгеретін шама
дербес мәндерін үздіксіз өзгеретін шама
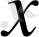 - пен:
- пен:
 ықтималдығын ықтималдық элементі
ықтималдығын ықтималдық элементі
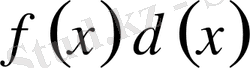 - пен, қосындысын интегралмен ауыстырсақ, (1) фомуласы былай жазылады:
- пен, қосындысын интегралмен ауыстырсақ, (1) фомуласы былай жазылады:
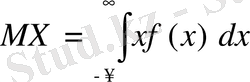 (3)
(3)
Ал егер де
Х -
тің мүмкін мәндері
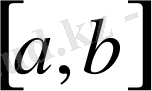 аралығында болса, онда
аралығында болса, онда
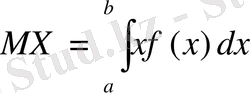 (3’)
(3’)
болады. (3) формуладағы
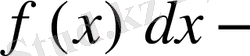 ті
ті
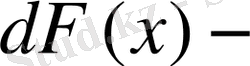 пен ауыстырып, мұны үлестіру функциясы арқылы былай да жазуға болады:
пен ауыстырып, мұны үлестіру функциясы арқылы былай да жазуға болады:
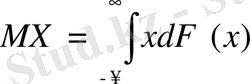 (4)
(4)
Математикалық күтімі болмайтын кездейсоқ шамалар да кездеседі. Мысалы,
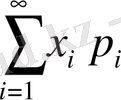 қатары жинақсыз болса, математикалық күтім болмайды, яғни
қатары жинақсыз болса, математикалық күтім болмайды, яғни
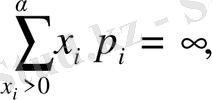
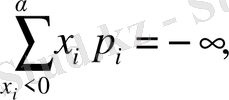
болса, онда Х - тің математикалық күтімі болмайды дейміз. Ал
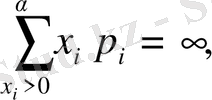
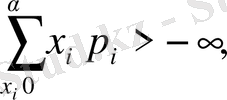
болса, онда
Х -
тің математикалық күтімі болады және ол
 деп аталады. Сондай - ақ
деп аталады. Сондай - ақ
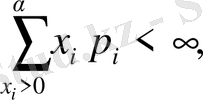
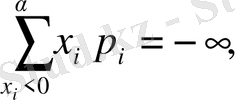
болса, онда
Х -
тің математикалық күтімі болады және ол
 делінеді. Біз өзіміздің қарастыруларымызда кездейсоқ шаманың математикалық күтімін бар, яғни сәйкес қатар немесе интеграл абсолют жинақты деп ұйғарамыз.
делінеді. Біз өзіміздің қарастыруларымызда кездейсоқ шаманың математикалық күтімін бар, яғни сәйкес қатар немесе интеграл абсолют жинақты деп ұйғарамыз.
Егер кездейсоқ шама орнына кездейсоқ функция
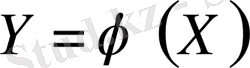 алынса, онда мұның математикалық күтімі
алынса, онда мұның математикалық күтімі
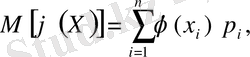 (5)
(5)
ал егер де
Х
үздіксіз кездейсоқ шама
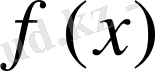 тығыздығымен берілсе, онда
тығыздығымен берілсе, онда
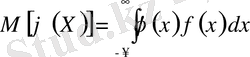 (6)
(6)
болады. Ескертетін бір мәселе бұл өрнектермен
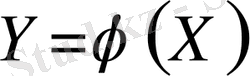 функциясының математикалық күтімін анықтау үшін бұл функцияның үлестіру заңын білу міндетті емес ол заң айқын берілмеуі мүмкін. Бірақ аргумент
Х -
тің үлестіру заңы берілуі қажетті де жеткілікті.
функциясының математикалық күтімін анықтау үшін бұл функцияның үлестіру заңын білу міндетті емес ол заң айқын берілмеуі мүмкін. Бірақ аргумент
Х -
тің үлестіру заңы берілуі қажетті де жеткілікті.
Бұл формулалар айнымалылар саны екі және одан көп болса да, орын алады. Мысалы,
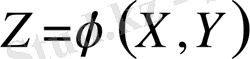
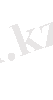
болса онда
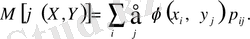 (5’)
(5’)
Үздіксіз кездейсоқ шамалар үшін
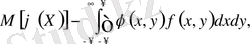
мұндағы
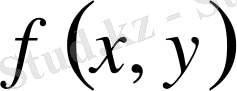 болса,
болса,
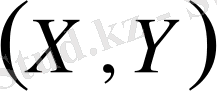 кездейсоқ шамалары жүйесінің үлестіру тығыздығы. Сондай - ақ,
кездейсоқ шамалары жүйесінің үлестіру тығыздығы. Сондай - ақ,
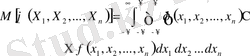
деп жазуға болады, мұндағы
f
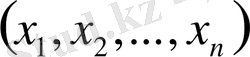 болса,
(Х
1,
Х
2
,
. . . ,
Х
п
) - жүйесінің үлестіру тығыздығы.
болса,
(Х
1,
Х
2
,
. . . ,
Х
п
) - жүйесінің үлестіру тығыздығы.
2 - м ы с а л. Бернулли схемасы бойынша үлестірілген кездейсоқ шаманың математикалық күтімін анықтау керек.
Шешуі: Бернулли схемасында биномдық үлестіру
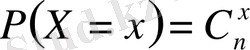
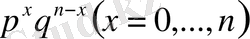
болатын. Олай болса, анықтама бойынша
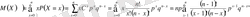
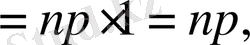
яғни
М(Х) =пр. (7)
3 - м ы с а л. Пуассон заңы бойынша үлестірілген кездейсоқ шаманың математикалық күтімін анықтау керек.
Ш е ш у і. Пуассон үлестіруі
х=0, 1, 2, . . .
болатын. Олай болса
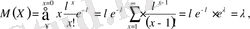
яғни М(Х) =
. Сонымен, параметр і, математикалық кү-
тім болды.
4-мысал. [a, b] аралығында бірқалыпты үлестірілген кездейсоқ шаманың математикалық күтімін анықтау керек.
Ш е ш у і.
Демек,
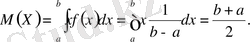
М(Х) = (b + а) /2. (9)
Қасиеттердің дәлелдемесін дискретті кездейсоқ шамалар үшін көрсетеміз. Ал кздейсоқ шама үздіксіз болса, онда оның берілген ықтималдық тығыздығы бойынша сәйкес формуланы пайдаланып, математикалық кү-тімді табамыз.
1°-қасиет. Тұрақты шаманың математикалық күтімі сол тұрақтыға тең, яғни М(С) = С.
Дәлелдеуі. Х-тің барлық мәндері тұрақты С-ның өзіне тең, яғни х
=х 2 = . . . =х п = С болатын кездейсоқ шама деп қарастыруымызға болады. Сонда
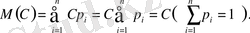
2°-қасиет. Тұрақтыны математикалық күтім таңбасының сыртына шығаруға болады, яғни М(СХ) == СМ(Х) .
Дәлелдеуі. СХ-ті кездейсоқ шама деп қарастыра-
мыз, сонда
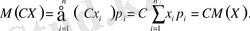
3° - к а с и е т. Екі кездейсоқ шама қосындысының математикалық күтімі олардың математикалық күтімде-рінің қосындысына тең, яғни
М(Х+Ү) =М(Х) +М(Ү) .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz