Комбинаторика мен ықтималдық теориясының теориялық физикаға қолданылуы


2. 3 КОМБИНАТОРИКАНЫҢ ЫҚТИМАЛДЫҚТАР ТЕОРИЯСЫНДА ЖӘНЕ ТЕОРИЯЛЫҚФИЗИКАДА ҚОЛДАНЫЛУЫ
2. 3. 1 Комбинаториканың қолданылуы
Анықтама. Тәжірибе жасамай оның нәтижесі жөнінде алдын ала болжам айтуға болмайтын экспериментті стохастық эксперимент деп атайды.
Кейбір жағдайда өзара бірін-бірі жоятын нәтижелердің болуы мүмкін, оны х 1 , х 2 , . . . , х n арқылы белгілейміз. х і нәтижеге сәйкес Р і =Р(x i ) деп жазамыз да, Р і - нақты сан, Р i >0, P 1 +P 2 +…+P n =1.
Егер кейбір Е оқиғасының болуы
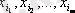 нәтижелердің біреуінен болса және басқа жағдайда болмаса, онда Е оқиғасының ықтималдығы
нәтижелердің біреуінен болса және басқа жағдайда болмаса, онда Е оқиғасының ықтималдығы
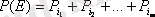 теңдігімен анықтаймыз. Бастапқы ықтималдықтардың P
1
, P
2
, …, P
n
жазылуы әр түрлі нәтижелердің салыстырмалы шындыққаұқсастығының бағалауын көрсетеді. Көптеген практикалық жағдайлардың тең мүмкіндікті nнәтижелерден тұратынын көруге болады. Сондықтан, P
1
=P
2
=…=P
n
=
теңдігімен анықтаймыз. Бастапқы ықтималдықтардың P
1
, P
2
, …, P
n
жазылуы әр түрлі нәтижелердің салыстырмалы шындыққаұқсастығының бағалауын көрсетеді. Көптеген практикалық жағдайлардың тең мүмкіндікті nнәтижелерден тұратынын көруге болады. Сондықтан, P
1
=P
2
=…=P
n
=
 . Бұл жағдайда Е оқиғасының ықтималдығы үшін m нәтижелердің мүмкіндік санын m-ді есептеу керек.
. Бұл жағдайда Е оқиғасының ықтималдығы үшін m нәтижелердің мүмкіндік санын m-ді есептеу керек.
6-мысал. 1-ден N-ге дейін нөмірленген N жәшіктер бар. Жәшіктерге n шамаларды кез келген амалмен орналастырамыз. Мұны n<N. 1-ден n-ге дейінгі жәшіктердің әрбіреуінде бір шар болатын ықтималдықты тап.
Бұл ықтималдық екі жағдайға байланысты:
1) Шарлар ажыратылған ба, әлде жоқ па?
2) (шығару принципі) негізгі ерекшеліктеріне байланысты бірлеспейтіндік орын ала ма, бір шары бар жәшікке екінші шарды салуға болмайды.
1) Егер n шарлар ажыратылған болса және негізгі ерекшелік - шығару принципі орын алмаса, онда N n тәсілдердің орналастырулары n шарлардың N жәшіктерге n! тәсілдермен олардың 1, 2, …, n нөмірлерін бір бірлеп орналастырады. Осындай жағдайлардан ықтималдықты былаанықтайды
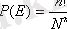 (2. 1. 1)
(2. 1. 1)
2) егер n шарлар ажыратылатын болса және бірлеспейтіндік орындалса, онда бірінші шарды N-ші жәшікке, екінші шарды (N-1) жәшікке, і-ші шарды (N-i+1) жәшікке орналастырады, сондықтан nшарлардың N жәшіктерге орналастыру саны
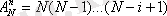
Бұл шарларды n! тәсілдермен 1, 2, …, n нөмірлерімен жәшіктерге орналастыру мүмкін және ізделініп отырған ықтималдық мынаған тең
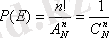 (2. 1. 2)
(2. 1. 2)
3) Егер шарлар ажыратылмайтын болса және бірлеспейтіндік орындалмайтын болса, онда теріс емес бүтін сан болатын х
1
+х
2
+…+х
n
=n теңдеуін шешу арқылы есептеуге келтіреді, мұнда х
і
жәшіктегішарлардың саны. Ол N элементінің n-нен жасалған қайталанбалы
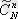 теруіне тең, яғни
теруіне тең, яғни
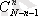 . Олардың бір шешімі
. Олардың бір шешімі
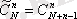
х 1 =х 2 =…=х n =1, х n+1 =…=х N =0.
Ондай жағдайда ізделініп отырған ықтималдық
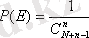 (2. 1. 3)
(2. 1. 3)
Ешқандай өзгешеліктері болмайтын терулер физика жағынан алғанда тең мүмкіндікті терулер екенін көрсетеді.
Егер шарларда ешқандай өзгешеліктер болмаса және бірлеспейтіндік орын алса, онда шарларды орналастыру тәсілдерінің саны қайталанбайтын N элементтің n-нен жасалған теруіне тең, яғни
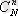 . Бірінші n жәшіктен алу бірден-бір мүмкіндік екенін көрсетеді және оның ықтималдығы (2. 1. 2) формула сияқты
. Бірінші n жәшіктен алу бірден-бір мүмкіндік екенін көрсетеді және оның ықтималдығы (2. 1. 2) формула сияқты
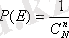
Бұдан мынадай қорытынды туады. Егер негізделген ерекшеліктерінде бірлеспейтіндік орын алса, онда ықтималдық шарлардың өзгешеліктеріне байланысты емес.
Статистикалық физика n кішкентай бөліктерден тұратын кейбір жиындарды қарастырады (протондар, нейтрондар, фотондар болуы мүмкін) ; олардың әрбіреуі кейбір N-нің бір күйінде болуы мүмкін (бұл энергетикалық деңгей болуы мүмкін) . Ол жүйенің n кішкентай бөліктерінің макроскопиялық күйі вектормен беріледі. Х=( х 1 , х 2 , …, х n ) .
Мұнда х і і күйдегі тұрған кішкентай бөліктердің саны. Р ықтималдықтың кейбір бөлігінің макроскопиялық олардың кішкентай бөліктері бір күйде тұруы мүмкін емес.
1) Егер кішкентай бөліктердің өзгешеліктері болса және негізгі ерекшеліктерінде бірлеспейтіндік орындалмаса, онда ықтималдық (2. 1. 1) формуламен беріледі де, онда бұл кішкентай бөліктер Максвелл-Больцманның классикалық статистикасына бағынады делінеді.
2) Егер кішкентай бөліктерде өзгешеліктер жоқ болса және негізгі ерекшеліктерінде бірлеспейтіндік орындалмаса, онда ықтималдық (2. 1. 3) формуламен беріледі, онда кішкене бөліктер Бозе-Эйнштейннің статистикасына бағынады делінеді. Фотондар және мезондар осындайларға жатады.
3) Егер кішкентай бөліктерде өзгешеліктер жоқ болса және негізгі ерекшеліктерінде бірлеспейтіндік орындалса, онда Р ықтималдық (2. 1. 2) формуламен беріледі де және ол Ферми-Дирактың статистикасына бағынадыі. Бұл электрондар, протондар, нейтрондар. (2. 1. 2) -формуладағы жағдай, өзгешеліктері бар кішкене бөліктерге жатады да, негізгі ерекшеліктерінде бірлеспейтіндік орын алады, бұл физикада кездеспейді.
Өте жоғары температурада N-күйлердің саны өте үлкен сан болғанда, әртүрлі макроскопиялық күйлер тең мүмкіндікте болады да, Ферми-Дирактың және Бозе-Эйнштейннің статистикалары, Максвел-Больцманның статистикасымен бірігіп кетеді.
Төменгі температурадағы энергетикалық деңгейдің төмен болуы мүмкін, ондай жағдайда келтірілген модельдерді бірін-бірінен айыру қиын.
1-есеп. n бөліктері бар, әр бөліктердің ықтималдықтары
 және ол N-нің (N>n) әрбір ұясында. Ықтималдықты табу керек: 1) анықталған n ұяда бөліктерден бір бөлік болады; 2) қандайда n бөліктерде бір бөлік болады.
және ол N-нің (N>n) әрбір ұясында. Ықтималдықты табу керек: 1) анықталған n ұяда бөліктерден бір бөлік болады; 2) қандайда n бөліктерде бір бөлік болады.
Шешуі. Бұл есеп қазіргі статистикалық физикада басты роль атқарады, оқиғалардың қалай құралғаны толық топ тең ықтималдығына байланысты Максвелл-Больцманның, Бозе-Эйнштейннің, Ферми-Дирактың статистикалық физикасына бағынатынын көрсетеді.
Максвелл-Больцманның статистикасында кез келген үлестірімдер бірі-бірінен сан мәнімен басқа олардың бөліктерімен айырмашылықта болады: әрбір ұяда 0-ден бастап n-ге дейін бөліктер орналасқан. Барлық мүмкіндіктегі үлестірімдерді төмендегі әдіс бойынша есептеп табамыз: әрбір бөлік әрбір N ұяда орналасқан, сондықтан, n бөліктердің мүмкін үлестірімі ұя бойынша
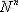 тәсілджерімен орналастырылған.
тәсілджерімен орналастырылған.
Бірінші сұрақ бойынша қолайлы жағдай туғызатын сан n!, олай болса, белгілі n ұяға бір бөліктің түсу ықтималдығы (2. 1. 1) формуламен анықталады.
Екінші сұрақ үшін қолайлы жағдай туғызатын
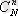 рет көп, олай болса, қандай да бір n ұяларға бір бөлік пайда болу ықтималдығы
рет көп, олай болса, қандай да бір n ұяларға бір бөлік пайда болу ықтималдығы
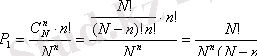
Бозе-Эйнштейннің статистикасындағы тең ықтималдықты жалпы санын есептеп шығарамыз. Ол үшін түзудің бойына ұяларды орналастырамыз. Содан кейін бөліктердің тең мүмкіндікті алмастыруларын және ұялардың өзара қоршауларын қарастырамыз.
Сонымен, бөліктердің ұялардағы орналасуы мен қоршаулардың орналасуы ұяларды толтыру кезінде қарастырылады.
Мұндағы алмастырулардың саны (N+n-1) !. Ол алмастырудың ішінде ұқсастары бар: әрбір улестірім ұя бойынша (N-1) ! рет саналады, себебі ұялардың арасында қандай қоршаулар болатынын ескердік, онан басқа ұялар бойынша әрбір үлестірім саны n!(N-1) ! Осыдан Бозе-Эйнштейннің ұялар бойынша бөліктерінің үлестірімдері
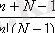 . Сондықтан Бозе-Эйнштейннің статистикасында
. Сондықтан Бозе-Эйнштейннің статистикасында
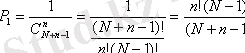
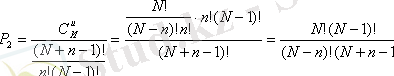
Ферми-Дирактың статистикасын қарастырамыз. Оның статистикасы бойынша ұяда мүмкін бір бөлік болуы, не болмауы: бөлшектердің жекеленуі құрылады. Әр түрлі үлестірімдердің ұялардағы жалпы санын Ферми-Дирактың статистикасында есептеп шығару оңай: бірінші бөлік N түрлі тәсілдермен, екіншісі (N-1), үшіншісі (N-2) және ақырында n-cі (N-n+1) түрлі тәсілдермен есептелінеді. Бөліктердің жеке бөліктерін жою үшін пайда болған санды n!-ға бөлу керек. Сондықтан, бөліктердің Nұяларға орналасу мүмкіндігі
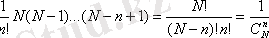
Сонымен Ферми-Дирактың статистикасында ізделінді ықтималдығы
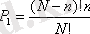 , Р
2
=1
, Р
2
=1
2. 2 Тәжірибелердің қайталануы
Егер тәжірибе бірнеше рет жүргізілгенде А оқиғасының әр тәжірибесіндегі ықтималдығы басқа тәжірибелердің нәтижесіне тәуелсіз үйлесімсіз болса, онда ондай тәжірибелерді А оқиғасына қарағанда тәуелсіз тәжірибелер деп атайды. әр түрлі тәуелсіз тәжірибелерде Аоқиғасының ықтималдығы да әр түрлі болуы немесе бірден болуы мүмкін. А оқиғасының барлық тәжірибелердегі ықтималдығы бірдей болатын жағдайды қарастырамыз.
Егер А оқиғасының әр тәжірибедегі пайда болу ықтималдығы р болса, онда А оқиғасының пайда болмау ықтималдығы q=1-p болады 1 .
А оқиғасының n тәуелсіз тәжірибеде k рет пайда болуының, n-k рет пайда болмауының ықтималдығын табу керек. Іздеп отырған ықтималдықты P n (k) арқылы белгілейміз.
Бұл есепті Бернулли формуласы шешеді.
2. 3 Бернулли формуласы
Бірнеше жай оқиғалардан құралған жиынтықты күрделі оқиға деп атайды.
Бір күрделі А оқиғасының n тәуелсіз тәжірибесінде k рет пайда болуының, (n-k) рет пайда болмауының ықтималдығы тәуелсіз оқиғаларды көбейту теоремасы бойынша:
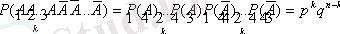
Бұл ықтималдық А оқиғасының қандай тәжірибеде пайда болуына байланысты емес, сондықтан, ізделінді ықтималдық P n (k) үйлесімсіз оқиғаларының ықтималдықтарының қосу ережесі бойынша
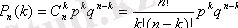
Бұл формуланы Бернулли формуласы деп атайды.
Биномдық үйлестірімнің ықтималдықтары Бернулли формуласымен анықталып, Ньютон формуласымен есептелінеді:
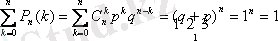
Оқиғаның n тәуелсіз тәжірибеде
а) k реттен аз;
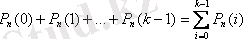 .
.
1 Бектаев Қ. Б. Ықтималдықтар теориясының негізгі ұғымдары: методикалық талдау / Қ. Б. Бектаев. - Алматы, 1977. - 106 бет.
б) k реттен көп;
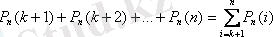 .
.
в) k реттен кем емес;
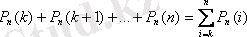
г) k реттен көп емес пайда болу ықтималдықтары:
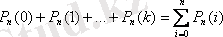 .
.
2-есеп. Шахмат ойнау шеберлігі тең екі шахматты ойын көрсетуде. Тең аяқтағанда есептемегенде
а) Екі партияның біреуін ұту мен төрт партияның екеуінің ұтудың ықтималдықтарын табу керек. Қайсысының ықтималдықтары жоғары.
б) Төрт партиядан 2-ден кем емес ұту мен бес партиядан 3-тен кем емес ұтыстың қайсысының ықтималдықтары жоғары.
Шешуі. Екі ойнау шеберлігі тең шахматшылар, сондықтан
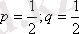 .
.
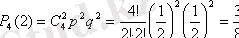 ,
,
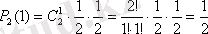 ,
,
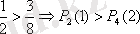 .
.
б)
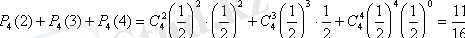
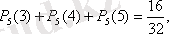
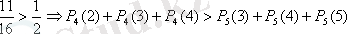
2. 4 Дискретті кездейсоқ шамалар. Гипергеометриялық үлестірім
3-есеп. Бидай тұқымының шығындылығы 80% болсын. Егілген 5 тұқым дәнінің мына ықтималдықтарын есептеңіздер:
а) үшеуден аз өседі;
б) өсетін дән саны үштен кем емес;
в) өсетін дән саны үштен аз;
г) өсетін дән үштен көп.
Шешуі. Әрбір тұқым дәнінің шығындылық ықтималдығы р=0, 8, онда шығынсыздығы q=1-p=1-0, 8=0, 2
a) n=5; k=3
Бернулли формуласы бойынша
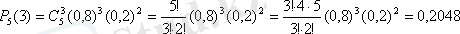
б) 3≤k≤4;
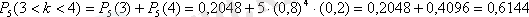
в) k<3;
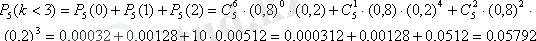
г) k>3;
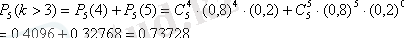
4-есеп. 4 баласы бар семьяда 3 қыз және 1 ұл бала болу ықтималдығын анықтау керек. Қыз және ұл баланың туу ықтималдығы бірдей.
Шешуі. Қыз баланың туу ықтималдығы р=0, 5, онда ұл баланың туу ықтималдығы да q=1-p=1- 0, 5=0, 5.
Ізделінді ықтималдық:
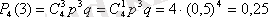
5-есеп. Күміс ақшаны 6 рет лақтырады. Ел таңба пайда болуы 3-тен көп болмау ықтималдығы қандай?
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz