Жойылмалы эллиптік түрдегі операторлардың бір класының өз-өзіне түйіндестігі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 48 бет
Таңдаулыға:
Мазмұны
Кіріспе .
1 Эллиптік түрдегі теңдеулер
1. 1 Лаплас теңдеуіне әкелетін есептер . . .
1. 2 Лаплас теңдеуін түрлендіру . . .
1. 3 Лаплас теңдеуінің кейбір дербес шешімдері . . .
2 Функционалдық анализдің негізгі түсініктері мен кейбір фактілері
2. 1 Метрикалық кеңістік түсінігі . . .
2. 2 Сызықты және нормаланған кеңістіктер . . .
2. 3 Гильберт кеңістігі, ортогональдық . . .
2. 4 Сызықты операторлар теориясының элементтері . . .
2. 5. Кері операторлар . . .
2. 6. Соболев кеңістігі . . .
3 Жойылмалы эллиптік түрдегі оператордың бір класының өз-өзіне түйіндестігін зерттеу . . .
3. 1 Өз-өзіне түйіндес операторлар . . .
3. 2 Жойылмалы эллиптік түрдегі оператордың бір класының өз-өзіне түйіндестігі . . .
Қорытынды . . .
Пайдаланылған әдебиеттер тізімі . . .
КІРІСПЕ
Тақырыптың өзектілігі. Эллиптiк түрдегі теңдеулер стационарлық (тұрақты) процестердi, мысалы, денеде тұрақты температураның таралуы, өткiзгiштiң бетiндегi электр зарядтарының тепе-теңдiк күйi, сұйықтың потенциалды ағысы т. с. с. процестердi сипаттайды.
Эллиптік түрдегі операторларға қарағанда, жойылмалы эллиптік түрдегі операторлардың спектральды сұрақтары аз зерттелген. Бұл бағыттағы немесе осыған жақын жұмыстар М. М. Смирновтың, Х. Трибелдің, М. В. Келдыштың, П. Боллей және Т. Камюдің, О. А. Олейниктің, М. Отелбаевтың, Т. Ш. Кальменовтың, М. Б. Муратбековтың, Л. К. Кусаинова мен М. С. Айтенованың және басқа да ғалымдардың еңбектерінде кездеседі.
Жұмыс мақсаты. Жұмыстың негізгі мақсаты жойылмалы эллиптік түрдегі оператордың бір класының өз-өзіне түйіндестігі.
Дипломдық жұмыс құрылымы. Жұмыс кіріспе, үш бөлім, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспеде тақырыптың өзектілігі негізделген, негізгі мақсаттары келтірілген, жұмыстың жаңалығы мен теориялық және практикалық маңыздылығы анықталған.
Бірінші бөлімде әдебиетке шолу жасалып, эллиптік түрдегі теңдеулердің кластарға бөлінуі, айнымалыны ажырату әдістері көрсетіліп мысалдармен ұштастырылған.
Екінші бөлімде функционалдық анализдің кейбір фактілері мен тұжырымдары және көмекші нәтижелер келтірілген.
Үшінші бөлімде жойылмалы эллиптік түрдегі оператордың бір класының өз-өзіне түйіндестігі көрсетілген.
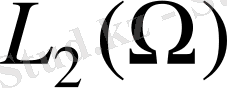 кеңістігінде
кеңістігінде
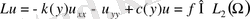 (1)
(1)
дифференциалдық операторды қарастырамыз. Мұндағы Ω={(x, y) : -π< x<π, 0<y<1} - тіктөртбұрыш.
(1) операторы
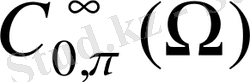 -
-
 облысындағы
у
айнымалысы бойынша барлық ретті дифференциалдары анықталған функциялар жиынында берілсін және
облысындағы
у
айнымалысы бойынша барлық ретті дифференциалдары анықталған функциялар жиынында берілсін және
 (2)
(2)
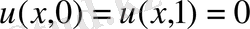 (3)
(3)
шарттарын қанағаттандырсын.
L операторының коэффициенттері төмендегі шарттарды қанағаттандырады:
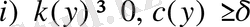 >0 - [0, 1] -де бөлікті үзіліссіз функциялар;
>0 - [0, 1] -де бөлікті үзіліссіз функциялар;
Теорема.
i) шарты орындалсын. Онда L операторы
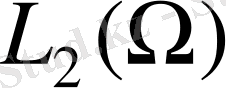 кеңістігінде өз-өзіне түйіндес.
кеңістігінде өз-өзіне түйіндес.
1 Эллиптiк түрдегі теңдеулер
1. 1 Лаплас теңдеуіне келтірілетін есептер
Эллиптiк түрдегі теңдеулер стационарлық (тұрақты) процестердi, мысалы, денеде тұрақты температураның таралуы, өткiзгiштiң бетiндегi электр зарядтарының тепе-теңдiк күйi, сұйықтың потенциалды ағысы т. с. с. процестердi сипаттайды. Осы сияқты процестердi зерттеулер Лаплас теңдеуiнiң шешiмiн табу амалына әкеледi. Лаплас теңдеуi
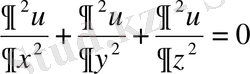 (1. 1. 1)
(1. 1. 1)
түрiнде жазылады.
Теңдеудiң сол жағына
 Лаплас операторын қолданып былай жазуға болады.
Лаплас операторын қолданып былай жазуға болады.
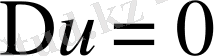
Екi тәуелсiз айнымалылар үшiн Лаплас теңдеуi
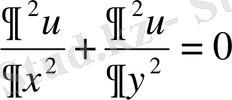
түрiнде, жазылады. Ал
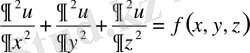
түрiндегi теңдеу Пуассон теңдеуi деп аталады.
Лаплас теңдеуiн қанағаттандыратын u функциялары гармоникалық функциялар деп аталады.
Бiртектi денеде температураның тұрақталып таралуы
Бiртектi
Т
денесi
 бетiмен шектелген болсын дейiк. Дененiң әртүрлi нүктелерiндегi температура
бетiмен шектелген болсын дейiк. Дененiң әртүрлi нүктелерiндегi температура
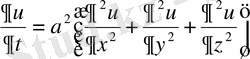
теңдеуiн қанағаттандырады. Егер температура уақыттан тәуелсiз болса, яғни
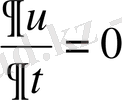 , онда дененiң температурасы Лаплас теңдеуiн қанағаттандырады.
, онда дененiң температурасы Лаплас теңдеуiн қанағаттандырады.
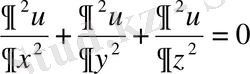
Осы теңдеуден дененiң температурасы бiр мәндi анықталуы үшiн
 бетiндегi температураны бiлу керек. Сондықтан (1. 1. 1) теңдеу үшiн шеттiк есеп былай қойылады:
бетiндегi температураны бiлу керек. Сондықтан (1. 1. 1) теңдеу үшiн шеттiк есеп былай қойылады:
1 0 Дирихле есебi (бiрiншi шеттiк есеп)
Берiлген
Т
облысында гармоникалық функция болатын, тұйық
 облысында үзiлiссiз және облыстың
облысында үзiлiссiз және облыстың
 шекарасында берiлген үзiлiссiз
шекарасында берiлген үзiлiссiз
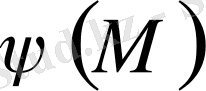 функциясына тең, яғни
функциясына тең, яғни
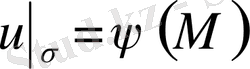 (1. 1. 2)
(1. 1. 2)
шартын қанағаттандыратын
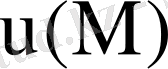 функциясын табу керек. Егер температураның таралуы жазықтықтағы
С
контуры мен
D
облысында қарастырылатын болса, онда
функциясын табу керек. Егер температураның таралуы жазықтықтағы
С
контуры мен
D
облысында қарастырылатын болса, онда
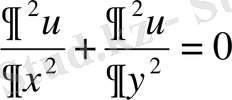
теңдеуiн қанағаттандыратын және
С
контурында
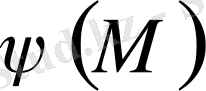 функциясына тең
u(x, y)
функциясын табу керек.
функциясына тең
u(x, y)
функциясын табу керек.
2 0 Нейман есебi (екiншi шеттiк есеп)
Берiлген
Т
облысында гармоникалық функция болатын, тұйық
 облысында үздiксiз дифференциалданатын, ал
облысында үздiксiз дифференциалданатын, ал
 тегiс бетiнен сыртқа қарай бағытталған нормаль бойынша алынған
тегiс бетiнен сыртқа қарай бағытталған нормаль бойынша алынған
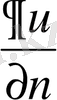 туындысы осы беттiң нүктелерiнде берiлген
туындысы осы беттiң нүктелерiнде берiлген
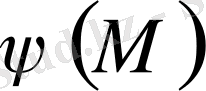 үздiксiз функциясына тең болатын, яғни
үздiксiз функциясына тең болатын, яғни
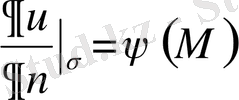 (1. 1. 3)
(1. 1. 3)
шартын қанағаттандыратын u(M) функциясын табу керек.
3 0 Аралас есеп (үшiншi шеттiк есеп)
Берiлген
Т
облысында гармоникалық болатын,
 тұйық облысында үздiксiз дифференциалданатын, ал сол
u(M)
функциясының және оның нормальдiк бағыт бойынша алынған
тұйық облысында үздiксiз дифференциалданатын, ал сол
u(M)
функциясының және оның нормальдiк бағыт бойынша алынған
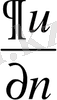 туындысының сызықтық комбинациясы
туындысының сызықтық комбинациясы
 тегiс бетiнде берiлген үздiксiз функциясына тең болатын, яғни
тегiс бетiнде берiлген үздiксiз функциясына тең болатын, яғни
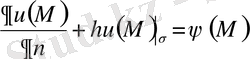 (1. 1. 4)
(1. 1. 4)
шартын қанағаттандыратын u(M) функциясын табу керек.
Егер есептiң шешiмiн
 бетiмен қоршалған iшкi облыста немесе одан сырт облыста табу керек болса, онда есеп тиiсiнше iшкi немесе сыртқы шеттiк есеп деп аталады.
бетiмен қоршалған iшкi облыста немесе одан сырт облыста табу керек болса, онда есеп тиiсiнше iшкi немесе сыртқы шеттiк есеп деп аталады.
Сұйықтың потенциалды ағыны
Екiншi мысал ретiнде сұйық ағынының көзi жоқ, яғни сығымдалмайтын сұйықтың потенциалды ағынын қарастырайық. Шекарасы
 болатын қандай да бiр
Т
облысының iшiнде
v(x, y, z)
жылдамдықпен сипатталатын сығымдалмайтын сұйықтың (тығыздығы
болатын қандай да бiр
Т
облысының iшiнде
v(x, y, z)
жылдамдықпен сипатталатын сығымдалмайтын сұйықтың (тығыздығы
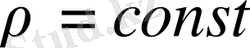 ) стационар ағыны бар болсын дейiк. Егер сұйық ағыны құйынсыз болса, онда
) стационар ағыны бар болсын дейiк. Егер сұйық ағыны құйынсыз болса, онда
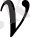 жылдамдығы потенциалдық вектор болады, яғни
жылдамдығы потенциалдық вектор болады, яғни
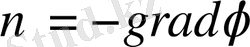 (1. 1. 5)
(1. 1. 5)
Мұндағы
 - жылдамдық потенциалы деп аталатын скалярлық функция. Егер ағын көздерi жоқ болса, онда
- жылдамдық потенциалы деп аталатын скалярлық функция. Егер ағын көздерi жоқ болса, онда
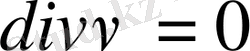
Осыны (1. 1. 5) теңдеуге қойып,

немесе
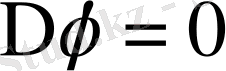
теңдеуiн аламыз. Осыдан потенциалдық жылдамдық Лаплас теңдеуiн қанағаттандыратынын көремiз.
1. 2 Лаплас теңдеуiн түрлендiру
Алдымен екi өлшемдi және үш өлшемдi кеңiстiктердегi негiзгi координаталар жүйелерiн еске салайық:
Екi өлшемдi кеңiстiктегi тiк бұрышты декарт координаталар жүйесi;
Үш өлшемдi кеңiстiктегi тiк бұрышты декарт координаталар жүйесi;
Екi өлшемдi кеңiстiктегi полярлық координаталар;
Үш өлшемдi кеңiстiктегi цилиндрлiк координаталар;
Үш өлшемдi кеңiстiктегi сфералық координаталар;
Полярлық координаталар мынадай арақатынастармен анықталады.
а)
y
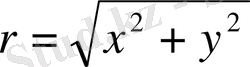 ,
,
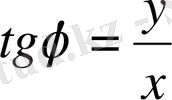 ,
,
немесе,
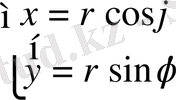
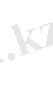
Цилиндрлік координаталаp
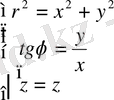
немесе
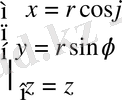
Сфералық координаталар
в)
1-сурет
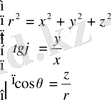
немесе
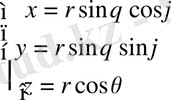
Лаплас теңдеуiнде полярлық координаталарға көшейiк:
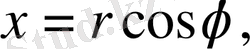
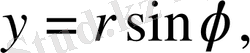
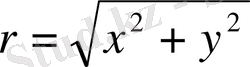 ,
,
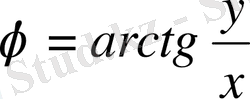 егер
x>0
болса,
егер
x>0
болса,
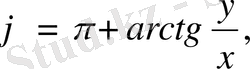 егер x<0,
егер x<0,
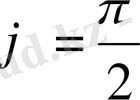 , егер x=0, y>0,
, егер x=0, y>0,
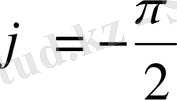 егер
x=0, y<0
егер
x=0, y<0
болғандықтан, мынадай түрлендiрулер жүргiземiз:
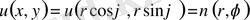
және
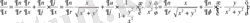
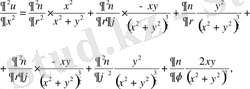
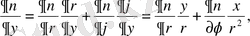

Осыларды теңдеуге қоямыз
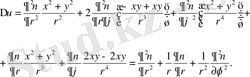
Сонымен
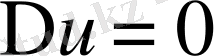 Лаплас теңдеуi полярлық координаталармен былай жазылады
Лаплас теңдеуi полярлық координаталармен былай жазылады
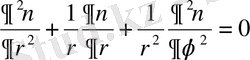 (1. 2. 1)
(1. 2. 1)
Лаплас теңдеуiнiң цилиндрлiк координаталармен берiлген түрi.
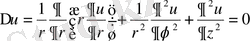 (1. 2. 2)
(1. 2. 2)
Лаплас теңдеуiнiң сфералық координаталармен берiлген түрi
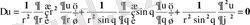 (1. 2. 3)
(1. 2. 3)
1. 3 Лаплас теңдеуiнiң кейбiр дербес шешiмдерi
Сфералық симметриялы
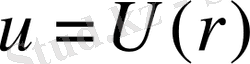 Лаплас теңдеуiнiң шешiмi
Лаплас теңдеуiнiң шешiмi
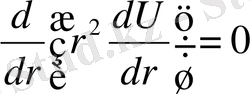
жай дифференциалдық теңдеуiнен анықталады. Бұл теңдеудi интегралдап,
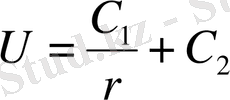
шешiмiн аламыз. Мұндағы С 1 және С 2 - кез-келген тұрақтылар. Егер С 1 =1, С 2 =0 деп алатын болсақ, онда Лаплас теңдеуiнiң кеңiстiктегi
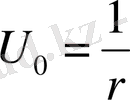 (1. 3. 1)
(1. 3. 1)
фундаменталды шешiмiн аламыз.
Осы сияқты
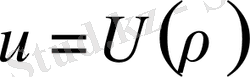 деп алып және (1. 2. 1) не (1. 2. 2) теңдеулердi пайдаланып, цилиндрлiк немесе дөңгелектi симметриялы болатын шешiм аламыз:
деп алып және (1. 2. 1) не (1. 2. 2) теңдеулердi пайдаланып, цилиндрлiк немесе дөңгелектi симметриялы болатын шешiм аламыз:
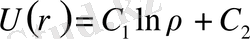
Егер С 1 =-1, С 2 =0 деп алатын болсақ, онда
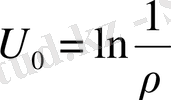 (1. 3. 2)
(1. 3. 2)
теңдiгiн аламыз. Бұл функцияны жазықтықтағы Лаплас теңдеуiнiң фундаменталды шешiмi деп атайды.
2
ФУНКЦИОНАЛДЫҚ АНАЛИЗДІҢ НЕГІЗГІ ТҮСІНІКТЕРІ МЕН КЕЙБІР ФАКТІЛЕРІ
- Метрикалық кеңістік түсінігі
Анализдің негізгі түсініктерінің бірі-шекке көшу. Бұл түсініктің негізінде элементтер арасындағы арақашықтықты анықтайтын скалярлық шама жатыр.
Анықтама 2. 1. 1. Жиын элементтерінің арақашықтығы (метрика) деп-төмендегідей шарттарды қанағаттандыратын
1.
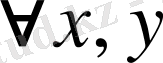
 ,
,
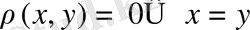
2.
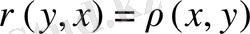
3.
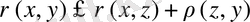
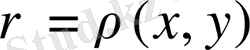 функциясын айтамыз.
функциясын айтамыз.
Анықтама 2. 1. 2. Егер жиында метрика енгізілген (анықталған) болса, онда ол метрикалық кеңістік деп аталады.
Сонымен, метрикалық кеңістік деп бос емес Х жиынынан және
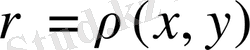 функциясынан құралған
функциясынан құралған
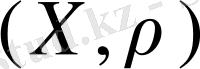 жұбын айтады.
жұбын айтады.
Мысалы, n-өлшемді
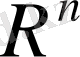 Евклид кеңістігінде метрика
Евклид кеңістігінде метрика
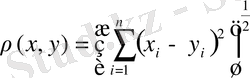
функциясымен анықталады.
Әрине, жиында метриканы әртүрлі әдіспен анықтауға болады. Бұл жағдайда әртүрлі метрика үшін алынған метрикалық кеңістіктер де әртүрлі болады.
Анализде кез келген жиында метрика анықтауға болатындығы дәлелденеді. Сондай-ақ
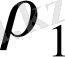 метрикасы анықталса, онда
метрикасы анықталса, онда
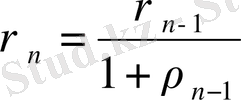 өрнегімен ақырсыз көп метрика анықтауға болады.
өрнегімен ақырсыз көп метрика анықтауға болады.
Элементтер арасындағы қашықтық ұғымына сүйене отырып мынандай түсініктерді енгізуге болады:
Анықтама 2. 1. 3.
X кеңістігіндегі центрі
 радиусы
радиусы
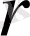 болатын ашық (тұйық) шар деп-
болатын ашық (тұйық) шар деп-
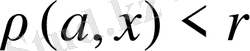 (
(
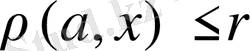 ) теңсіздігін қанағаттандыратын X кеңістігінің бөлігін айтамыз және
) теңсіздігін қанағаттандыратын X кеңістігінің бөлігін айтамыз және
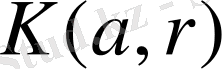 деп белгілейміз.
деп белгілейміз.
Анықтама 2. 1. 4.
Егер
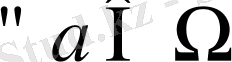 үшін
үшін
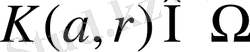 болатындай шар табылса онда
болатындай шар табылса онда
 жиыны ашық деп аталады.
жиыны ашық деп аталады.
Анықтама 2. 1. 5.
 элементінің аймағы деп
элементінің аймағы деп
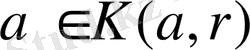 болатын кез келген ашық шарды немесе ашық жиынды айтамыз.
болатын кез келген ашық шарды немесе ашық жиынды айтамыз.
Айталық
 болсын.
болсын.
Анықтама 2. 1. 6.
 нүктесі
нүктесі
 жиынының шектік нүктесі деп аталады, егер
жиынының шектік нүктесі деп аталады, егер
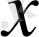 -тің әрбір аймағы
-тің әрбір аймағы
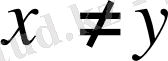 болатын кемінде бір
болатын кемінде бір
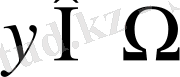 элементін қамтитын болса.
элементін қамтитын болса.
Анықтама 2. 1. 7.
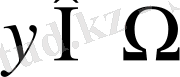 оңашаланған нүкте деп аталады, егер осы элементті қамтитын қандай да бір
оңашаланған нүкте деп аталады, егер осы элементті қамтитын қандай да бір
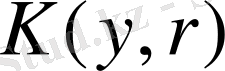 аймағы үшін
аймағы үшін
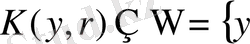 болса.
болса.
Анықтама 2. 1. 8.
Егер
 элементті қамтитын қандай да бір
элементті қамтитын қандай да бір
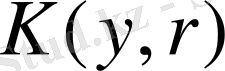 аймағы үшін толығымен
аймағы үшін толығымен
 жиынына енетін болса онда
жиынына енетін болса онда
 ішкі нүкте деп аталады, .
ішкі нүкте деп аталады, .
Анықтама 2. 1. 9.
 жиынының толықтаушысы деп-оның барлық шектік нүктелерінің жиынын айтамыз және
жиынының толықтаушысы деп-оның барлық шектік нүктелерінің жиынын айтамыз және
 деп белгілейміз.
деп белгілейміз.
Метрикалық кеңістіктегі компактілік.
Компакті жиындар (компакт жиындар) жиындар классификациясында маңызды рөлге ие.
Анықтама 2. 2. 1.
Егер
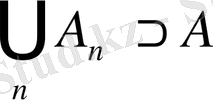 болса,
болса,
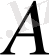 жиынының ашық бүркеуі деп
жиынының ашық бүркеуі деп
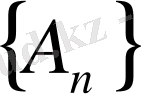 жиындар топтамасын айтамыз.
жиындар топтамасын айтамыз.
Жиынды бүркейтін мұндай жиындар топтамалары (бүркеулер) біреу емес екендігін ескертейік.
Анықтама 2. 2. 2.
Егер
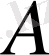 жиынының әрбір ашық бүркеуінен саны арқылы ішкі бүркеу бөліп алуға болатын болса онда
жиынының әрбір ашық бүркеуінен саны арқылы ішкі бүркеу бөліп алуға болатын болса онда
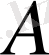 жиыны компакті немесе компакт деп аталады.
жиыны компакті немесе компакт деп аталады.
Компакт жиындардың келесі қасиеттерін дәлелдеусіз келтіреміз [1:34; 35] :
1. Компакті метрикалық кеңістіктің тұйық ішкі жиыны компакт.
2. Компакті метрикалық кеңістіктің үзіліссіз бейнелеу кезіндегі
образы компакт.
3. n-өлшемді
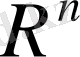 евклид кеңістігінде компактілік тұйықтық пен
евклид кеңістігінде компактілік тұйықтық пен
шектелгендікке эквивалентті.
4.
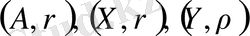 метрикалық кеңістіктері үшін
метрикалық кеңістіктері үшін
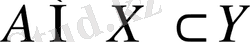
болсын, онда
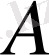 бір мезгілде
бір мезгілде
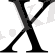 және
және
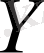 кеңістіктерінде
кеңістіктерінде
компакті.
Компакті жиындардың жоғарыдағы анықтамаға эквивалент тағы бір анықтамасын келтірейік.
Айталық
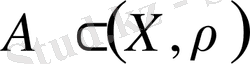 және
және
 болсын.
болсын.
Анықтама 2. 2. 3.
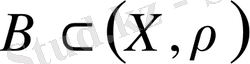 жиыны
жиыны
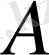 жиынына
жиынына
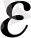 тор деп аталады, егер
тор деп аталады, егер
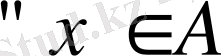 үшін
үшін
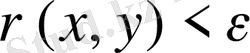 болатындай
болатындай
 табылса.
табылса.
Компактілікті тағайындайтын келесі критерийді дәлелдеусіз қабылдаймыз.
Теорема 2. 2. 1.
 метрикалық кеңістігі компакт болу үшін
метрикалық кеңістігі компакт болу үшін
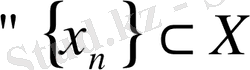 тізбегінен жинақты ішкі тізбек бөлінуі қажетті және жеткілікті.
тізбегінен жинақты ішкі тізбек бөлінуі қажетті және жеткілікті.
Теорема 2. 2. 2.
 толық метрикалық кеңістік және
толық метрикалық кеңістік және
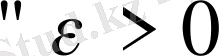 үшін
үшін
 кеңістігінде ақырлы
кеңістігінде ақырлы
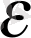 тор бар болса, сонда тек сонда ғана
тор бар болса, сонда тек сонда ғана
 компакт болады.
компакт болады.
Метрикалық кеңістіктегі толықтық
Метрикалық кеңістіктің көптеген фундаментальды қасиеттері оның толықтығына сүйенеді.
Анықтама 2. 2. 4.
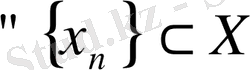 тізбегі фундаментальды деп аталады, егер
тізбегі фундаментальды деп аталады, егер
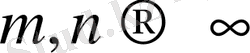 болғанда
болғанда
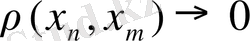 болса.
болса.
Фундаментальды тізбекті Коши тізбегі деп атайды.
Егер
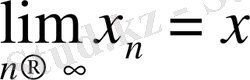 және
және
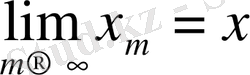 болса, онда
болса, онда
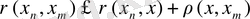 теңсіздігінің негізінде
теңсіздігінің негізінде
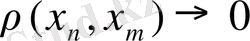 болатындығын көру қиын емес. Яғни егер
болатындығын көру қиын емес. Яғни егер
 жинақты тізбек болса, онда ол тізбек фундаментальды тізбек болады. Жалпы жағдайда кері тұжырым дұрыс емес. Кейбір нақты кеңістіктердің ерекшеліктеріне байланысты бұл ұғымдар эквивалент болады. Мысалы,
жинақты тізбек болса, онда ол тізбек фундаментальды тізбек болады. Жалпы жағдайда кері тұжырым дұрыс емес. Кейбір нақты кеңістіктердің ерекшеліктеріне байланысты бұл ұғымдар эквивалент болады. Мысалы,
 нақты сандар кеңістігінде бұл тұжырымдардың эквивалент екендігін білдіретін Коши критерийі бар. Осыған байланысты келесі түсінікті енгізейік.
нақты сандар кеңістігінде бұл тұжырымдардың эквивалент екендігін білдіретін Коши критерийі бар. Осыған байланысты келесі түсінікті енгізейік.
Анықтама 2. 2. 5.
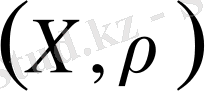 метрикалық кеңістігі толық деп аталады, егер мұндағы әрбір фундаментальды тізбек осы кеңістіктің элементіне жинақталатын болса. Яғни
метрикалық кеңістігі толық деп аталады, егер мұндағы әрбір фундаментальды тізбек осы кеңістіктің элементіне жинақталатын болса. Яғни
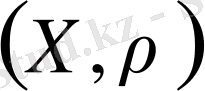 толық
толық
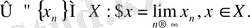
Осы тұрғыдан берілген метрикалық кеңістікті қандай да бір әдіспен толықтыруға болады ма?-деген орынды сұрақ туады. Бұл сұраққа төмендегі теорема жауап береді. Теореманы енгізбес бұрын бірқатар түсініктерді енгізейік.
Анықтама 2. 2. 6.
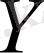 метрикалық кеңістігі
метрикалық кеңістігі
 кеңістігінің толықтаушысы деп аталады, егер
кеңістігінің толықтаушысы деп аталады, егер
 және
және
 болса.
болса.
Анықтама 2. 2. 7.
 және
және
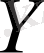 метрикалық кеңістіктері изометриялы деп аталады, егер олардың арасындағы арақашықтықты сақтайтын өзара бірмәнді сәйкестік бар болса, яғни
метрикалық кеңістіктері изометриялы деп аталады, егер олардың арасындағы арақашықтықты сақтайтын өзара бірмәнді сәйкестік бар болса, яғни
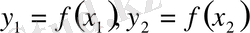
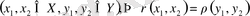 .
.
Теорема 2. 2. 3.
Әрбір
 метрикалық кеңістігінің
метрикалық кеңістігінің
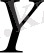 толықтаушысы бар болады және бұл толықтаушысы изометрия дәлдігінде жалғыз болады.
толықтаушысы бар болады және бұл толықтаушысы изометрия дәлдігінде жалғыз болады.
Метрикалық кеңістіктерге мысалдар
1)
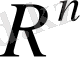 кеңістігінде кез келген әртүрлі реттелген
кеңістігінде кез келген әртүрлі реттелген
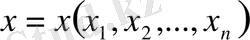 және
және
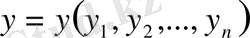 нүктелері үшін метриканы мына түрде аламыз.
нүктелері үшін метриканы мына түрде аламыз.
.
мұндағы:
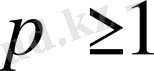 .
.
1) және 2) аксиомалардың орындалатыны жеңіл көрініп тұр.
3) аксиоманың орындалатынын тексерейік
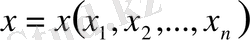 ,
,
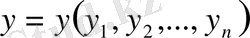 және
және
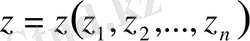 болсын.
болсын.
Дәлірек айтқанда біз мынадай теңсіздікті дәлелдеуіміз керек
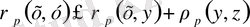 (2)
(2)
Егер
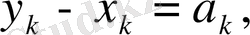
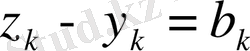
деп белгілесек, онда
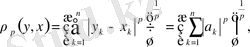
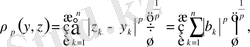
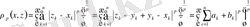
Енді (2) теңсіздік пен соңғы келтірілген теңсіздіктерді пайдаланып жазсақ мынадай түрге енеді.
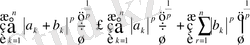 -
бұл Миньковский теңсіздігі
,
-
бұл Миньковский теңсіздігі
,
олай болса (2) теңсіздігі орындалады. Бұл метрикалық кеңістікті
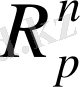 -
деп белгілейміз.
-
деп белгілейміз.
2)
 болғанда бұл кеңістік n-өлшемді арифметикалық
болғанда бұл кеңістік n-өлшемді арифметикалық
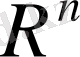 евклид кеңістігіне айналады.
евклид кеңістігіне айналады.
3) Барлық нақты сандардың шектелген тізбегін жиынын қарастырайық:
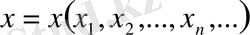 ,
,
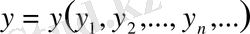 осы жиынның кез келген екі элементі болсын
осы жиынның кез келген екі элементі болсын
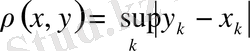
бұл метрика 1) - 3) аксиомаларды қанағаттандырады. Сондықтан аталған жиын метрикалық кеңістік болады, оны
 деп белгілейміз.
деп белгілейміз.
4)
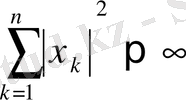 теңсіздігін қанағаттандыратын шексіз
теңсіздігін қанағаттандыратын шексіз
 сан тізбектерінің жиынын қарастырайық. Оны
сан тізбектерінің жиынын қарастырайық. Оны
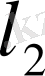 деп белгілейміз.
деп белгілейміз.
Осы жиында кез келген екі элементтің арақашықтығы
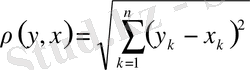
теңдігі арқылы анықтасақ ол метрикалық кеңістікке айналады. Ол үшін мынадай элементар теңсіздікті пайдаланамыз.
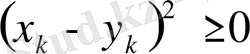
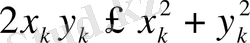

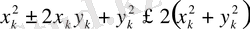
немесе
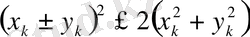
Соңғы теңсіздіктен
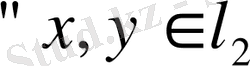 үшін
үшін
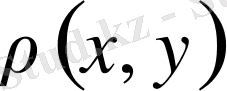 шамасының мағынасы бар болады, немесе
шамасының мағынасы бар болады, немесе
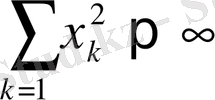
және
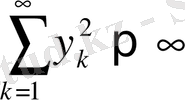

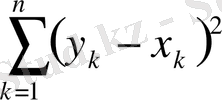
1) және 2) аксиомалардың орындалуы жеңіл дәлелденеді, ал 3) аксиома мына төмендегі теңсіздіктерден шығады (р=2 болғанда Миньковский теңсіздігі)
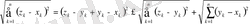
Бұл теңсіздікте
 шекке көшу арқылы мына теңсіздікті аламыз
шекке көшу арқылы мына теңсіздікті аламыз
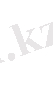
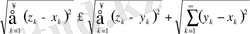
Бұл кеңістік
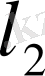 кеңістігі деп аталады.
кеңістігі деп аталады.
Дәл осы жолмен
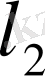 кеңістігін
кеңістігін
 -ге жалпылауға болады.
-ге жалпылауға болады.
Енді функционалдық метрикалық кеңістіктерге бірнеше мысалдар келтірейік
5)
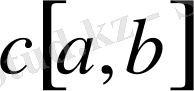 кеңістігі.
кеңістігі.
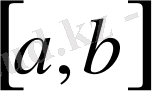 кесіндісінде анықталған үзіліссіз функциялар жиынында
кесіндісінде анықталған үзіліссіз функциялар жиынында
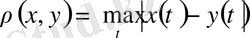
Метрикасын енгіземіз. Бұл үш аксиоманы да онай қанағаттандырады. Сондықтан
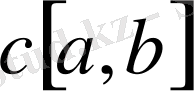 -метрикалық кеңістік,
-метрикалық кеңістік,
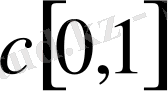 -ді
-ді
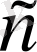 деп те белгілейміз.
деп те белгілейміз.
6)
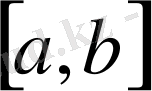 кесіндісінде анықталған үзіліссіз функциялар жиын, онда
кесіндісінде анықталған үзіліссіз функциялар жиын, онда
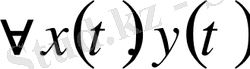 функцияларының арақашықтығы
функцияларының арақашықтығы
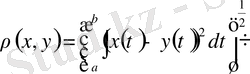
Бұл метрикалық кеңістік болады, оны
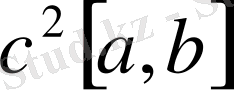 белгілейміз. 1), 2) аксиомалар оңай орындалады. 3) аксиома Миньковский интегралдық теңсіздігінен шығады. р=2 болғанда
белгілейміз. 1), 2) аксиомалар оңай орындалады. 3) аксиома Миньковский интегралдық теңсіздігінен шығады. р=2 болғанда
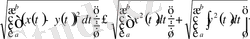
2. 2. Сызықты және нормаланған кеңістіктер.
Анықтама 2. 2. 1.
 жиыны сызықты кеңістік деп аталады, егер
жиыны сызықты кеңістік деп аталады, егер
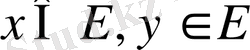 үшін осы элементтердің қосындысы деп аталатын, келесі шарттарды қанағаттандыратын
үшін осы элементтердің қосындысы деп аталатын, келесі шарттарды қанағаттандыратын
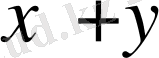 амалы анықталса:
амалы анықталса:
1. егер
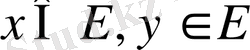 болса, онда
болса, онда
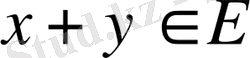
2.
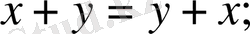 ;
;
3.
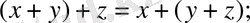
4. Барлық
 үшін
үшін
 болатын «нөлдік» элемент бар және
болатын «нөлдік» элемент бар және
 жиынында келесі шарттарды қанағаттандыратын
жиынында келесі шарттарды қанағаттандыратын
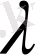 санына көбейту амалы анықталса:
санына көбейту амалы анықталса:
5. егер
болса, онда
болады(мұндағы
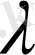
скаляр шама) ;
6.
-скалярлар;
7.

8. (сол жағында нөл саны, ал оң жағында
«нөлдік» элемент) ;
9.
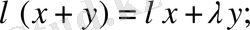
10.
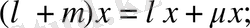
Мұнда
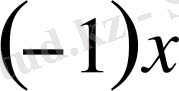 элементі
элементі
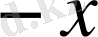 арқылы белгіленеді. Жоғарыдағы қасиеттерден
арқылы белгіленеді. Жоғарыдағы қасиеттерден
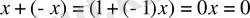 және
және
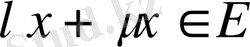 болатынын көреміз.
болатынын көреміз.
Кей жағдайда сызықты кеңістікті векторлық кеңістік деп, ал оның элементтерін векторлар деп атайды. Сызықтық кеңістікте
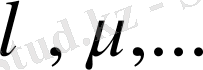 скаляр көбейткіштері нақты немесе комплекст болуына байланысты кеңістік те нақты немесе комплекс деп аталады.
скаляр көбейткіштері нақты немесе комплекст болуына байланысты кеңістік те нақты немесе комплекс деп аталады.
Мысалдар:
- Барлық нақты(комплекс) сандар жиыны нақты (комплекс) сызықтық кеңістік құрайды.
- Нақты(комплекс) коэффициентті бір айнымалы
көпмүшеліктер жиыны нақты(комплекс) сызықты кеңістік болады.
Анықтама 2. 3. 2.
Сызықтық кеңістіктің
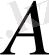 жиыны осы кеңістіктің ішкі кеңістігі деп аталады, егер
жиыны осы кеңістіктің ішкі кеңістігі деп аталады, егер
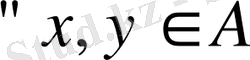 және
және
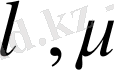 скалярлары үшін
скалярлары үшін
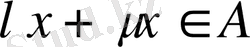 болса. Мұндай ішкі кеңістікті сызықты көпбейне деп атайды.
болса. Мұндай ішкі кеңістікті сызықты көпбейне деп атайды.
Кеңістіктің элементтерінің ұзындығы анықталған кеңістікті нормаланған кеңістік деп атайды.
Анықтама 2. 3. 3.
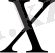 сызықты кеңістігінің әрбір
сызықты кеңістігінің әрбір
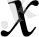 элементіне келесі шарттарды қанағаттандыратын
элементіне келесі шарттарды қанағаттандыратын
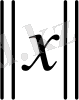 санын сәйкестендірсек:
санын сәйкестендірсек:
1.
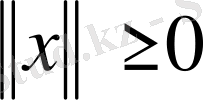 және
және
 ;
;
2.
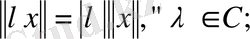
3.
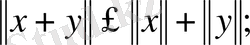
онда
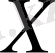 кеңістігі нормаланған кеңістік деп аталады.
кеңістігі нормаланған кеңістік деп аталады.
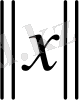 санын
санын
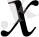 элементінің нормасы деп атаймыз. Егер
элементінің нормасы деп атаймыз. Егер
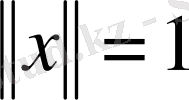 болса, онда
болса, онда
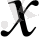 нормаланған элемент деп аталады. Мысалы, нақты(комплекс) сандар жиынында норма ретінде санның абсолют шамасын алсақ, онда ол нормаланған сызықты кеңістік болады. Сызықты нормаланған кеңістіктерде элементтердің арасындағы қашықтық ұғымын енгізуге болады. Нақты айтқанда келесі тұжырым орынды болады:
нормаланған элемент деп аталады. Мысалы, нақты(комплекс) сандар жиынында норма ретінде санның абсолют шамасын алсақ, онда ол нормаланған сызықты кеңістік болады. Сызықты нормаланған кеңістіктерде элементтердің арасындағы қашықтық ұғымын енгізуге болады. Нақты айтқанда келесі тұжырым орынды болады:
Лемма 2. 3. 1. .
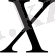 сызықты нормаланған кеңістігі
сызықты нормаланған кеңістігі
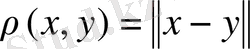 метрикасымен метрикалық кеңістік болады.
метрикасымен метрикалық кеңістік болады.
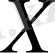 кеңістігінде осы метрика бойынша тізбектің жинақтылығы норма бойынша жинақтылықпен сай келеді.
кеңістігінде осы метрика бойынша тізбектің жинақтылығы норма бойынша жинақтылықпен сай келеді.
Лемма 2. 3. 2. Сызықты нормаланған кеңістікте норма метрика мағынасында үзіліссіз функция болып табылады.
Анықтама 2. 3. 4. Егер сызықты нормаланған кеңістік
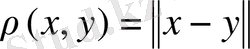
метрикасы бойынша толық метрикалық кеңістік болса онда сызықты нормаланған кеңістік толық деп аталады.
Толық сызықты нормаланған кеңістік банах кеңістігі деп аталады.
Теорема 2. 3. 1. Әрбір сызықты нормаланған кеңістік қандайда бір банах кеңістігіне енеді және сол кеңістікте тығыз болады.
2. 3. Гильберт кеңістігі.
Анализде функциялардың скаляр көбейтіндісі кеңінен қолданылады. Сондықтан скаляр көбейтінді енгізілген сызықты кеңістікті қарастырған жөн болады.
Анықтама 2. 3. 1.
Айталық
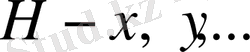 элементтерінің қандай да бір жиыны болсын.
элементтерінің қандай да бір жиыны болсын.
I. Егер
 жиынында
жиынында
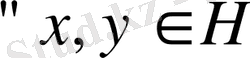 үшін келесі шарттарды қанағаттандыратын скаляр көбейтінді
үшін келесі шарттарды қанағаттандыратын скаляр көбейтінді
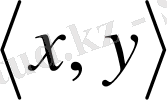 енгізілсе:
енгізілсе:
1.
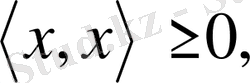 және
және
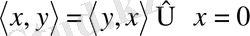
2.
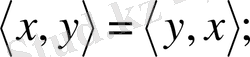
3.
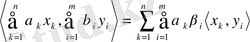 ;
;
II.
 жиынында
жиынында
 үшін n сызықты тәуелсіз векторлар табылса, яғни
үшін n сызықты тәуелсіз векторлар табылса, яғни
 ақырсыз өлшемді болса, онда
ақырсыз өлшемді болса, онда
 абстрактылы гильберт кеңістігі немесе гильберт кеңістігі деп аталады.
абстрактылы гильберт кеңістігі немесе гильберт кеңістігі деп аталады.
Гильберт кеңістігінде элементінің нормасы
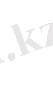
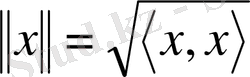
арқылы енгізіледі.
Бұл өрнекпен енгізілген
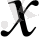 элементінің нормасы норма аксиомаларын қанағаттандыратынын көру қиын емес.
элементінің нормасы норма аксиомаларын қанағаттандыратынын көру қиын емес.
Гильберт кеңістігінде
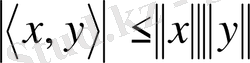
теңсіздігі орынды болады. Бұл теңсіздік Коши-Буняковский-Шварц теңсіздігі деп аталады.
Гильберт кеңістігінде метрика
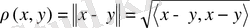
теңдігі бойынша анықталады және осы метрика мағынасында Н толық кеңістік болып табылады.
Егер
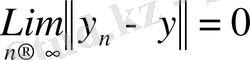
және
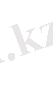
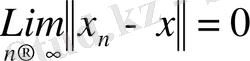 болса, онда
болса, онда
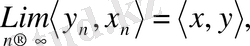
яғни скаляр көбейтіндінің үзіліссіздігі орынды.
Гильберт кеңістігіндегі ортогональдық.
Анықтама 2. 3. 2.
Гильберт кеңістігінің
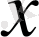 және
және
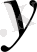 элементтері ортогональды деп аталады, егер
элементтері ортогональды деп аталады, егер
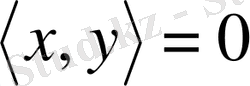 болса және
болса және
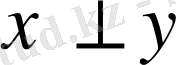 деп белгілейді.
деп белгілейді.
Егер
 үшін
үшін
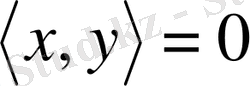 болса, онда
болса, онда
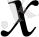 элементі
элементі
 жиынына ортогональ делінеді,
жиынына ортогональ делінеді,
 деп жазылады.
деп жазылады.
Теорема 2. 3. 1.
Егер
 және
және
 болса, онда
болса, онда
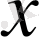 элементінің
элементінің
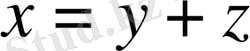 жіктелуі бар және ол жалғыз. Мұндағы
жіктелуі бар және ол жалғыз. Мұндағы
 ал
ал
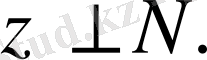
Салдар.
 кеңістігі ортогональды қосындыға жіктеледі, яғни
кеңістігі ортогональды қосындыға жіктеледі, яғни
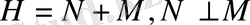
Лемма 2. 3. 1.
 сызықты көпбейнесі
сызықты көпбейнесі
 кеңістігінде барлық жерде тығыз болу үшін
кеңістігінде барлық жерде тығыз болу үшін
 көпбейнесіне ортогональ нөлден өзгеше элементтің болмауы қажетті және жеткілікті
көпбейнесіне ортогональ нөлден өзгеше элементтің болмауы қажетті және жеткілікті
Дәлелдеуі:
Қажеттілігі:
Айталық
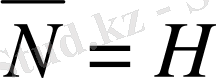 және
және
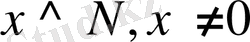 бар болсын
бар болсын
 , онда
, онда
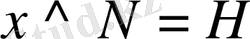 . Демек
. Демек
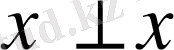 , олай болса
, олай болса

Жеткіліктілігі:
Айталық
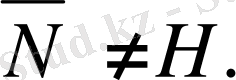 Олай болса
Олай болса
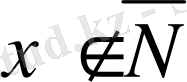 табылып, алдыңғы теорема бойынша
табылып, алдыңғы теорема бойынша
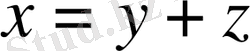 жіктелуі бар болады. Мұндағы
жіктелуі бар болады. Мұндағы
 , ал
, ал
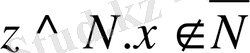 болғандықтан
болғандықтан
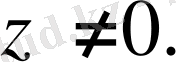 Ал бұл теорема шартына қайшы.
Ал бұл теорема шартына қайшы.
Рисс теорамасы
 -гильбертті кеңістік және
-гильбертті кеңістік және
 кеңістігінің тұйықталған ішкі кеңістігі болсын.
кеңістігінің тұйықталған ішкі кеңістігі болсын.
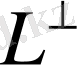 арқылы
арқылы
 -тағы
-тағы
 -дегі әр векторға ортогональді болатын барлық векторлардың жиынын белгілейміз,
-дегі әр векторға ортогональді болатын барлық векторлардың жиынын белгілейміз,
яғни (х, у) =0,
 ,
,
 .
.
2. 3. 1 леммасы
.
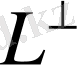 жиыны -
жиыны -
 кеңістігінің тұйықты сызықты ішкі кеңістігі болады.
кеңістігінің тұйықты сызықты ішкі кеңістігі болады.
Дәлелдеуі.

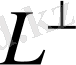 болсын, онда барлық
болсын, онда барлық
 үшін (х, у) =0. Бұдан
үшін (х, у) =0. Бұдан
 екендігін тексеру қиын болмайды, өйткені
екендігін тексеру қиын болмайды, өйткені
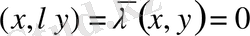 , мұндағы
, мұндағы
 - кезкелген комплексті сан. Келесі y
1
, у
2
∈
- кезкелген комплексті сан. Келесі y
1
, у
2
∈
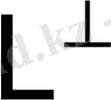 болсын, онда
болсын, онда
y
1
+у
2
∈
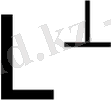 . Шынында, (х, у
1
+у
2
) = (х, у
1
) +(х, у
2
) = 0. Сондықтан,
. Шынында, (х, у
1
+у
2
) = (х, у
1
) +(х, у
2
) = 0. Сондықтан,
 - М кеңістігінің сызықты ішкі кеңістігі болады.
- М кеңістігінің сызықты ішкі кеңістігі болады.
Енді
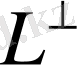 -дің тұйықтылығын тексереміз.
-дің тұйықтылығын тексереміз.
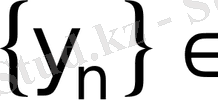
 және
және
 да
да
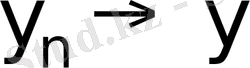 болсын, онда кезкелген х∈L үшін скалярлық көбейтіндінің үздіксіздігінен
болсын, онда кезкелген х∈L үшін скалярлық көбейтіндінің үздіксіздігінен
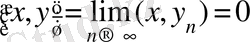
болады. Бұдан
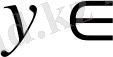
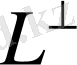 екендігі келіп шығады.
екендігі келіп шығады.
Теорема 2. 3. 1.
 - гильбертті кеңістік және
- гильбертті кеңістік және
 Equation. 3 - оның тұйықталынған сызықты ішкі кеңістігі болсын, онда
Equation. 3 - оның тұйықталынған сызықты ішкі кеңістігі болсын, онда
 -тың кез-келген элементі
-тың кез-келген элементі
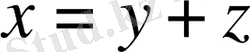 (2. 3. 1)
(2. 3. 1)
түрінде жалғыз ғана болып көрсетіледі. Мұндағы,
 L, z ∈
L, z ∈
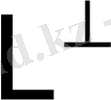 .
.
Дәлелдеуі. (2. 3. 1) қатынасының біреу ғана болатындығын дәлелдейік. Мысалы, (2. 3. 1) қатынасымен қатар
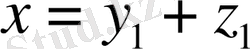 (2. 3. 2)
(2. 3. 2)
мұндағы
 ,
,
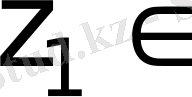
 , қатынасы да орын алсын.
, қатынасы да орын алсын.
Онда бұдан
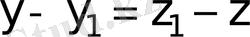 орын алады.
орын алады.
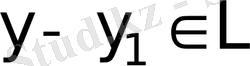 ,
,

 болса, онда
болса, онда
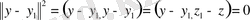 яғни
яғни
 , олай болса
, олай болса
 . Жалғыздылығы (біреу ғана болатындылығы) дәлелденді.
. Жалғыздылығы (біреу ғана болатындылығы) дәлелденді.
Енді (2. 3. 1) қатынасының бар болатындығын дәлелдейік.
Екі жағдайды қарастырамыз:
- Егер, онда, яғни теорема дәлелденді.
- болсын. Онда х нүктесінен L жиынына дейінгі ара қашықтық
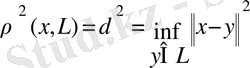
формуласы бойынша анықталады.
Берілген жағдайда
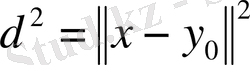 және
және
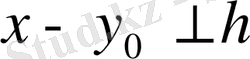 болатындай
болатындай
 элементінің бар болатындылығын көрсетуіміз керек, мұндағы
элементінің бар болатындылығын көрсетуіміз керек, мұндағы
 -дегі кезкелген элемент.
-дегі кезкелген элемент.
Сол үшін
inf
анықтамасын пайдаланамыз:
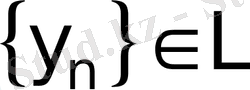 және
және
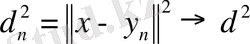 болатындай
болатындай
 тізбегі табылады. Енді
тізбегі табылады. Енді
 тізбегінің фундаментальді болатындығын көрсетеміз.
тізбегінің фундаментальді болатындығын көрсетеміз.
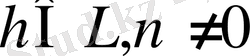 және
және
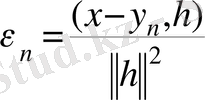 (2. 3. 3)
(2. 3. 3)
деп аламыз.
 және
және
 болатындықтан,
болатындықтан,
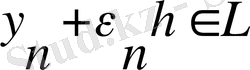 болады және
inf
анықтамасына сәйкес
болады және
inf
анықтамасына сәйкес
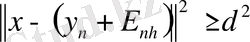 (2. 3. 4)
(2. 3. 4)
тізбегін аламыз. Осы соңғы теңсіздікті ашып жазайық:
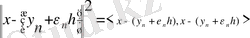
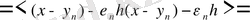
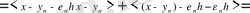
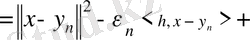
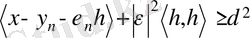
Бұдан және (2. 3. 3) -тен
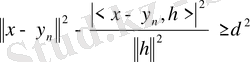
немесе
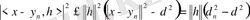
немесе
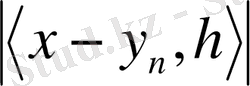
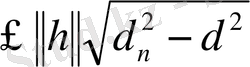 (2. 3. 5)
(2. 3. 5)
келіп шығады.
Тікелей есептеу жүргізе отырып,

екенін аламыз.
Бұдан
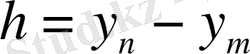 болғанда (2. 3. 5. ) -ті ескере отырып, мыналарды табамыз:
болғанда (2. 3. 5. ) -ті ескере отырып, мыналарды табамыз:
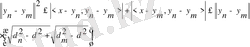
немесе
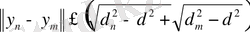
Осы соңғы теңсіздік
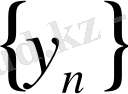 -нің фундаментальды тізбек екендігін көрсетеді. Н-тың толықтығынан
-нің фундаментальды тізбек екендігін көрсетеді. Н-тың толықтығынан
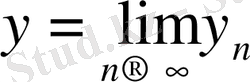 элементі бар болады.
элементі бар болады.
 тұйықталған болғандықтан
тұйықталған болғандықтан
 . Сонымен, біз
. Сонымен, біз
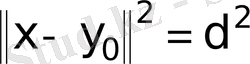
болатындығын дәлелдедік.
Енді
 -ден алынған кезкелген
-ден алынған кезкелген
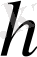 үшін
үшін
 ортогональ болатындығын көрсету керек болады. Ол үшін
ортогональ болатындығын көрсету керек болады. Ол үшін
 -да (2. 3. 5) -те шекке көше отырып,
-да (2. 3. 5) -те шекке көше отырып,
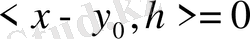
екендігін аламыз, яғни
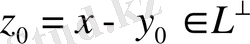 .
.
Сондықтан
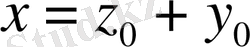
теорема толық дәлелденді.
Ескерту. Біз Н кеңістігінің тікелей қосынды
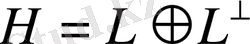
түріндегі бейнелеуін алып отырмыз.
Бұл жағдайда олардың тікелей қосындысы да ортогональды қосынды болады. Мына қатынастардың орын алуы да орынды:
 ,
,
 .
.
Н гильбертті кеңістігінде
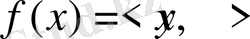 функционалын қарастырамыз, мұндағы у нөлге тең емес Н-тан алынған нақты элемент.
функционалын қарастырамыз, мұндағы у нөлге тең емес Н-тан алынған нақты элемент.
Лемма 2. 3. 2. .
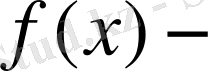 сызықты және шектеулі функционал, және
сызықты және шектеулі функционал, және
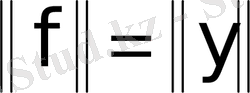
теңдігі орындалады.
Дәлелдеуі
 болсын, онда
болсын, онда
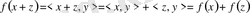
және
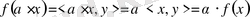
Коши теңсіздігіне сәйкес
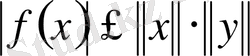
деп алуымызға болады, сондықтан
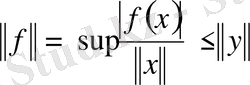 (2. 3. 6)
(2. 3. 6)
Екінші жағынан
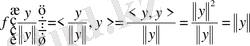 .
.
Бұдан
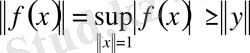 (2. 3. 7)
(2. 3. 7)
(2. 3. 6) - (2. 3. 7) теңсіздіктері лемманы дәлелдейді.
 арқылы кезкелген сызықты үздіксіз
арқылы кезкелген сызықты үздіксіз
 функционалының барлық нөлдері жинағын, яғни
функционалының барлық нөлдері жинағын, яғни
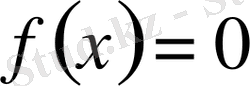
теңдеуінің түбірлерін белгілейік.
Лемма 2. 3. 3. К- Н кеңістігінің сызықты тұйықталған ішкі кеңістігі болады.
Дәлелдеуі.
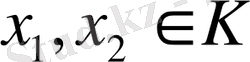 болсын, онда
болсын, онда
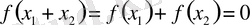
Бұл элемент
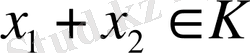 деген сөз. Енді
деген сөз. Енді
 , ал
, ал

кезкелген комплексті сан болсын, онда
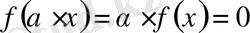 ,
,
яғни
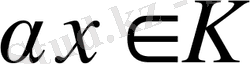 . Сызықтылығы дәлелденді.
. Сызықтылығы дәлелденді.
Енді
 -ның тұйықталған ішкі кеңістік болатындығын дәлелдейміз. Шынында, егерде
-ның тұйықталған ішкі кеңістік болатындығын дәлелдейміз. Шынында, егерде
 ,
,
 болса, онда функционалдың үздіксіздігінен
болса, онда функционалдың үздіксіздігінен

болады, яғни
 . Сондықтан
. Сондықтан
 - тұйықталған сызықты ішкі кеңістік.
- тұйықталған сызықты ішкі кеңістік.
Лемма толық дәлелденді.
Ф. Рисс теоремасы. Кез келген үзіліссіз сызықты функционал Н гильбертті кеңістігінде
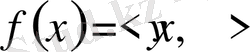 ,
,
 ,
,
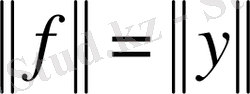
түрінде көрсетіледі.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz