Тұрақты коэффициентті біртекті матрицалық сызықты жүйелер: матрицалық экспонента, фундаментальдық матрица және Жордан формасы


МАТРИЦАЛЫҚ ӘДІС
Коэффициенттері нақты сандар болатын біртекті сызықты дифференциалдық жүйені

қарастыралық. Мынадай векторлы-матрицалық белгілеулер
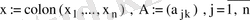 енгізу арқылы бұл жүйені векторлық теңдеу
енгізу арқылы бұл жүйені векторлық теңдеу
 (1)
(1)
түрінде жазуға болады.
Экспоненциалдық матрица
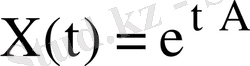 (2)
(2)
(1) жүйенің матрицалық шешімі болып табылады. Себебі ол -
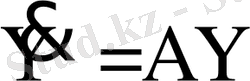 матрицалық теңдеуінің шешімі. Шынында да
матрицалық теңдеуінің шешімі. Шынында да
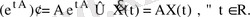
Аталған
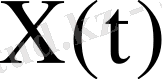 матрицасы
матрицасы
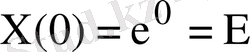 шартын қанағаттандырады. Олай болса,
шартын қанағаттандырады. Олай болса,
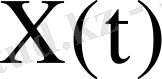 - (1) жүйенің нақты фундаментальдық матрицасы. Сондықтан (1) жүйенің жалпы шешімі
- (1) жүйенің нақты фундаментальдық матрицасы. Сондықтан (1) жүйенің жалпы шешімі
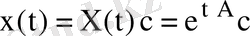 (3)
(3)
түрінде болады. Мұндағы
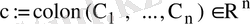 еркін тұрақты вектор.
еркін тұрақты вектор.
Егер (1) жүйеге қосымша бастапқы шарт
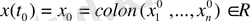 (4)
(4)
қойылса, онда (3) шешімі бұл шартқа қойып, с векторының мәнін анықтаймыз:

 -ның бұл табылған мәнін (3) формулаға қойып,
-ның бұл табылған мәнін (3) формулаға қойып,
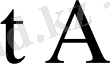 матрицасы мен (
матрицасы мен (
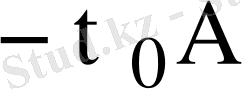 ) матрицасының коммутативтік қасиетін ескеріп (1) , (3) Коши есебінің шешімін
) матрицасының коммутативтік қасиетін ескеріп (1) , (3) Коши есебінің шешімін
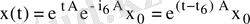
аламыз. Бұл формула мысалда дәйекті жуықтау әдісін қолдану арқылы да дәлелденген болатын.
Егер
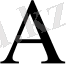 матрицасын комплекс сандар өрісінде Жордан формуласына келтіретін матрицаны
матрицасын комплекс сандар өрісінде Жордан формуласына келтіретін матрицаны
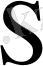 арқылы белгілесек
арқылы белгілесек
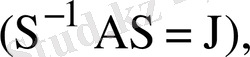 онда
онда
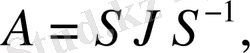 болады да, (2) фундаментальдық матрица былай
болады да, (2) фундаментальдық матрица былай
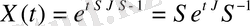
өрнектеледі. Фундаментальдық матрицаны оң жағынан ерекше емес
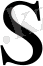 матрицасына көбейту арқылы алынатын
матрицасына көбейту арқылы алынатын
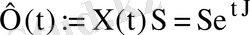 матрицасы да фундаментальдық матрица болып табылады. Ол -
матрицасы да фундаментальдық матрица болып табылады. Ол -
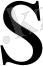 нақты болса, нақты, ал комплекс болса комплекс матрица болады.
нақты болса, нақты, ал комплекс болса комплекс матрица болады.
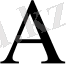 мактрицасының барлық меншікті сандары нақты болса, онда
мактрицасының барлық меншікті сандары нақты болса, онда
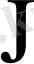 матрицасы нақты болғандықтан
матрицасы нақты болғандықтан
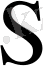 матрицасы да нақты болады. Бұл жағдайда
матрицасы да нақты болады. Бұл жағдайда
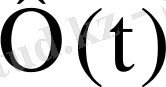 - нақты фундаментальдық матрица. Егер А матрицасының меншікті сандарының арасында комплекс мәнділері де бар болса, онда
- нақты фундаментальдық матрица. Егер А матрицасының меншікті сандарының арасында комплекс мәнділері де бар болса, онда
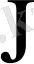 матрицасы комплекс мәнді болғандықтан
матрицасы комплекс мәнді болғандықтан
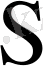 матрицасы да комплекс мәнді болады. Бұл жағдайда
матрицасы да комплекс мәнді болады. Бұл жағдайда
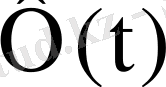 комплекс фундаментальдық матрица.
комплекс фундаментальдық матрица.
1
0
.
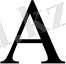 матрицасының барлық меншікті сандары нақты болсын. Оларға сәйкес табылатын элементар бөлгіштердің жай немесе еселі болуларына байланысты екі жағдай қарастыралық.
матрицасының барлық меншікті сандары нақты болсын. Оларға сәйкес табылатын элементар бөлгіштердің жай немесе еселі болуларына байланысты екі жағдай қарастыралық.
I жағдай.
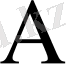 матрицасының барлық элементар бөлгіштері жай бөлгіштер болады деп есептейік:
матрицасының барлық элементар бөлгіштері жай бөлгіштер болады деп есептейік:
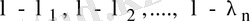 . Онда
. Онда
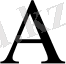 матрицасының Жордан формасы таза диагональдық, яғни
матрицасының Жордан формасы таза диагональдық, яғни
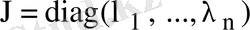 түрінде болады да, экспоненциалдық матрица
түрінде болады да, экспоненциалдық матрица
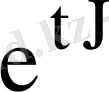 мына түрде
мына түрде
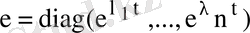
жазылады. Сондықтан жалпы шешім бұл жағдайда мына түрде
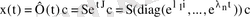
болады. Мұндағы
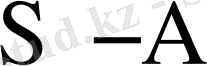 мтрицасын Жордан формасына келтіретін матрица. Егер
мтрицасын Жордан формасына келтіретін матрица. Егер
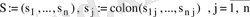
болса, онда
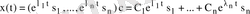 (5)
(5)
болады. Мұндағы
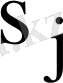 -
-
 матрицасының
матрицасының
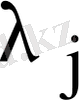 меншікті санына сәйкес келетін меншікті векторы. Олар нақты мәнді.
меншікті санына сәйкес келетін меншікті векторы. Олар нақты мәнді.
II жағдай . А матрицасының элементар бөлгіштері ішінде еселілері бар немесе олардың бәрі бірдей еселі:
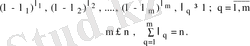
онда А матрицасының Жордан формасы
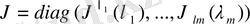
түрінде болады. Бұл жағдайда
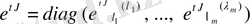
болғандықтан, жалпы шешімді мына түрде аламыз:
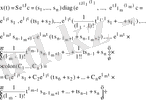
мұндағы
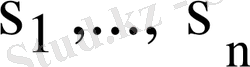 векторларының аорасында
векторларының аорасында
 векторы меншікті де, ал қалған
векторы меншікті де, ал қалған
 векторлары теріс болып табылады. Фундаментальдық матрицаға кіретін
векторлары теріс болып табылады. Фундаментальдық матрицаға кіретін
 шешім
шешім
 группаға бөлінеді ( элементар бөлшектерді саны қанша болса, соншаға) . әртүрлі группадағы шешімдердің дәрежесіне тең болады. Атап айтқанда бірінші группада
группаға бөлінеді ( элементар бөлшектерді саны қанша болса, соншаға) . әртүрлі группадағы шешімдердің дәрежесіне тең болады. Атап айтқанда бірінші группада
 , екінші группада
, екінші группада
 , т. с. с
, т. с. с
 - группада
- группада
 шешімдер бар. әр группадағы, мысалы
шешімдер бар. әр группадағы, мысалы
 -
-
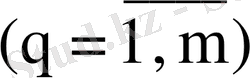 группадағы, шешімдердің түрлері мынадай:
группадағы, шешімдердің түрлері мынадай:

Әрбір
 группадағы шешімдердің мынадай қасиеті бар: кез келген орында тұрған шешімдегі
группадағы шешімдердің мынадай қасиеті бар: кез келген орында тұрған шешімдегі
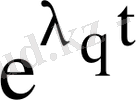 көрсеткіштік функциясына көбейтіліп тұрған векторлық көпмүшелік одан кейінгі орында тұрған шешімдігі
көрсеткіштік функциясына көбейтіліп тұрған векторлық көпмүшелік одан кейінгі орында тұрған шешімдігі
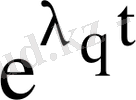 функциясына көбейтіліп тұрған векторлық көпмүшіеліктің туындысына тең. Яғни
функциясына көбейтіліп тұрған векторлық көпмүшіеліктің туындысына тең. Яғни
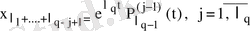 .
.
Мұнда
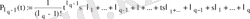
ал
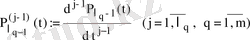
2 0 . Енді характерисикалық сандар арасында комплекс мәнділері болатын жағдайды қарастырайық.
Характеристикалық теңдеудің бір ғана комплекс мәнді
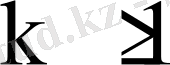 еселі
еселі
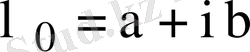 түбірлері бар болсын, онда
түбірлері бар болсын, онда
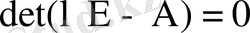 теңдеуінің коэффициенттері нақты сандар болғандықтан
теңдеуінің коэффициенттері нақты сандар болғандықтан
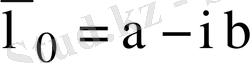 саны да бұл теңдеудің
саны да бұл теңдеудің
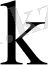 еселі түбірі болады. Қарастырып отырған жағдайды тағы да екі ішкі жағдайға бөлейік.
еселі түбірі болады. Қарастырып отырған жағдайды тағы да екі ішкі жағдайға бөлейік.
I жағдай.
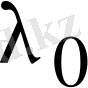 - санына сәйкес келетін элементар бөлшектердің бәрі жай
- санына сәйкес келетін элементар бөлшектердің бәрі жай
 :
:
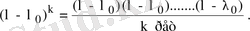
Бұл жағдайда
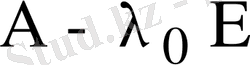 матрицасының рангі
матрицасының рангі
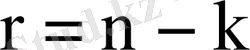 теңдігін қанағаттандыратын кезде болады. Ал
теңдігін қанағаттандыратын кезде болады. Ал
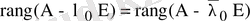 болғандықтан бұл жағдайда
болғандықтан бұл жағдайда
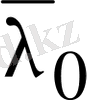 санына да
санына да
 жай элементар бөлшектер
жай элементар бөлшектер
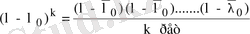
сәйкес келеді. Әлбетте
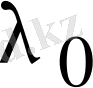 ,
,
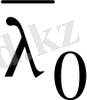 сандарына сәйкес келетін меншікті векторлар жалпы алғанда комплекс мәнді болады. Ілгеріде
сандарына сәйкес келетін меншікті векторлар жалпы алғанда комплекс мәнді болады. Ілгеріде
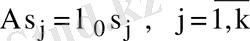 мен
мен
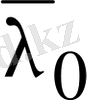 сандарына мына тіңдіктерді
сандарына мына тіңдіктерді

қанағаттандыратын
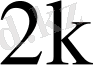 сызықты тәуелсіз (комплекс мәнді) меншікті векторлар сәйкес келетіні көрсетілді. Мұндағы
сызықты тәуелсіз (комплекс мәнді) меншікті векторлар сәйкес келетіні көрсетілді. Мұндағы
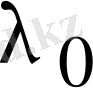 санына сәйкес келетін әрбір
санына сәйкес келетін әрбір
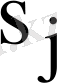 векторы мен
векторы мен
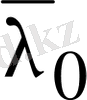 санына сәйкес келетін
санына сәйкес келетін
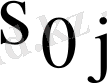 векторы өзара комплексті түйіндес болып келеді. Шынында да бір формуладан
векторы өзара комплексті түйіндес болып келеді. Шынында да бір формуладан
 ,
,
демек
 . Бұл жағдайда меншікті векторлар А матрицасын Жордан матрицасына келтіретін
. Бұл жағдайда меншікті векторлар А матрицасын Жордан матрицасына келтіретін
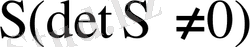 матрицасының тік жолдарын беретін болғандықтан, бұл матрица да комплекс мәні болады. Және оның
матрицасының тік жолдарын беретін болғандықтан, бұл матрица да комплекс мәні болады. Және оның
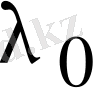 санына сәйкес келетін
санына сәйкес келетін
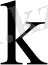 меншікті векторлары мен
меншікті векторлары мен
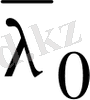 санына сәйкес келетін
санына сәйкес келетін
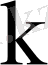 меншікті векторлары өзара комплексті түйіндес болады. әлбетте бұл жағдайда
меншікті векторлары өзара комплексті түйіндес болады. әлбетте бұл жағдайда
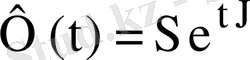
фундаментальдық матрицасы да комплекс мәнді болады (S және
 матрицалары комплекс мәнді) .
матрицалары комплекс мәнді) .
Егер нақты шешімдерден тұратын фундаментальдық матрица алғымыз келсе, онда
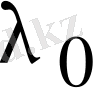 ,
,
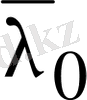 сандарына сәйкес келетін сызықты тәуелсіз нақты шешімдерді қарастырыуымыз керек. Меншікті сан
сандарына сәйкес келетін сызықты тәуелсіз нақты шешімдерді қарастырыуымыз керек. Меншікті сан
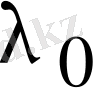 -ге сәйкес келетін
-ге сәйкес келетін
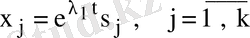
комплекс шешшімдерді мына тұрде жазайық:
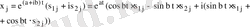
мұнда
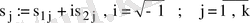 .
.
А нақты матрица болғандықтан әрбір
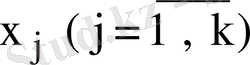 шешімнің нақты бөлігі
шешімнің нақты бөлігі
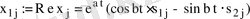
мен жорамал бөлігі
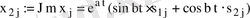
өз алдарына (1) жүйенің нақты шешімдері болады. Шынында да

бұл
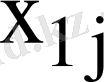 ,
,
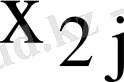 шешімдері өзара сызықты тәуелсіз болады. Меншікті
шешімдері өзара сызықты тәуелсіз болады. Меншікті
 санына сәйкес келетін әрбір
санына сәйкес келетін әрбір
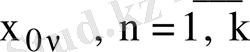 шешімі
шешімі
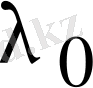 меншікті санына сәйкес келетін
меншікті санына сәйкес келетін
 шешіміне комплексті түйіндес болады. Сондықтан олардың нақты бөліктері өзара тең ал жорамал бөліктері тең таңбаларының қарама-қарсылығымен ажыратылады. Олай болса,
шешіміне комплексті түйіндес болады. Сондықтан олардың нақты бөліктері өзара тең ал жорамал бөліктері тең таңбаларының қарама-қарсылығымен ажыратылады. Олай болса,
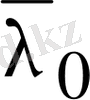 түбірі сызықты тәуелсіз нақты шешімдер тудырмайды. Яғни бұл жағдайда
түбірі сызықты тәуелсіз нақты шешімдер тудырмайды. Яғни бұл жағдайда
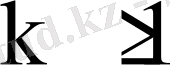 еселі
еселі
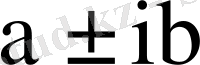 меншікті сандарын
меншікті сандарын
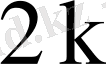 сызықты тәуелсіз нақты шешімдер сәйкес келеді. Бұларды қалған барлық меншікті сандарға сәйкес табылатын сызықты тәуелсіз нақты шешімдермен біріктіріп, нақты шешімдердің базисін не
фундаментальдық шешімдер жүйесін
аламыз. Олардан құрылған матрица (1) жүйенің нақты фундаментальдық матрицасын береді.
сызықты тәуелсіз нақты шешімдер сәйкес келеді. Бұларды қалған барлық меншікті сандарға сәйкес табылатын сызықты тәуелсіз нақты шешімдермен біріктіріп, нақты шешімдердің базисін не
фундаментальдық шешімдер жүйесін
аламыз. Олардан құрылған матрица (1) жүйенің нақты фундаментальдық матрицасын береді.
II жағдай
. Меншікті
 санына сәйкес келетін элементар бөлгіштердің ішінде еселілері бар, немесе олардың бәрі бірдей еселі болсын:
санына сәйкес келетін элементар бөлгіштердің ішінде еселілері бар, немесе олардың бәрі бірдей еселі болсын:
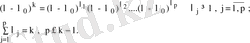
Бұл жағдай
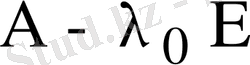 матрицасының рангі
матрицасының рангі
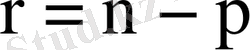 теңдігін қанағаттандыратын кезде болады. Түйіндес
теңдігін қанағаттандыратын кезде болады. Түйіндес
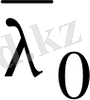 санына сәйкес келетін элементар бөлшектерде осы түрде болады. Меншікті
санына сәйкес келетін элементар бөлшектерде осы түрде болады. Меншікті
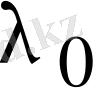 ,
,
 сандарының әрқайсысына
сандарының әрқайсысына
 меншікті,
меншікті,
 тіркес векторлар сәйкес келеді. Бұл жағдайда да
тіркес векторлар сәйкес келеді. Бұл жағдайда да
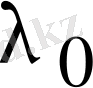 санына сәйкес келетін осы аттас векторларға комплекс түйіндем болады. Шынында да тіркес векторлар үшін
санына сәйкес келетін осы аттас векторларға комплекс түйіндем болады. Шынында да тіркес векторлар үшін

ал меншікті векторлар үшін мынадай теңдіктер дәлелденеді. Сондықтан
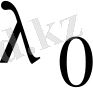 мен
мен
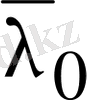 түбірлерінің әрқайсысына
түбірлерінің әрқайсысына
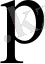 группадан тұратын өзара сызықты тәуелсіз комплекс мәнді
группадан тұратын өзара сызықты тәуелсіз комплекс мәнді
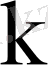 шешімдер сәйкес келеді. әрбір
шешімдер сәйкес келеді. әрбір
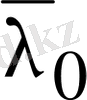 санына қатысты табылған шешімдер
санына қатысты табылған шешімдер
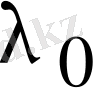 санына қатысты табылған сәйкес (сәйкес векторлар арқылы есептелетін) шешімдерге комплекс түйіндес болып келеді. Олай болса
санына қатысты табылған сәйкес (сәйкес векторлар арқылы есептелетін) шешімдерге комплекс түйіндес болып келеді. Олай болса
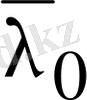 саны
саны
 санына сәйкес табылған шешімдермен сызықты тәуелсіздікте болатын жаңа нақты шешімдер тудырмайды. Яғни комплексті түйіндес
санына сәйкес табылған шешімдермен сызықты тәуелсіздікте болатын жаңа нақты шешімдер тудырмайды. Яғни комплексті түйіндес
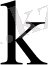 еселі
еселі
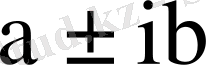 меншікті сандарына өзара сызықты тәуелсіз
меншікті сандарына өзара сызықты тәуелсіз
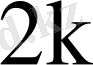 нақты шешімдер сәйкес келеді. Бұл сәйкес табылатын нақты шешімдермен біріктіріп, (1) жүйенің нақты базисін аламыз. әлбетте базисті құрайтын шешімдердің саны
нақты шешімдер сәйкес келеді. Бұл сәйкес табылатын нақты шешімдермен біріктіріп, (1) жүйенің нақты базисін аламыз. әлбетте базисті құрайтын шешімдердің саны
 -ге тең болады.
-ге тең болады.
Егер комплекс мәнді бірнеше меншікті сан болса, онда олардың әрқайысы үшін осы айтылғандарды қайталаймыз.
Сонымен меншікті сандардың арасында нақтылары мен қатар комплекс мәнділері де болатын жалпы жағдайда фундаментальдық матрица
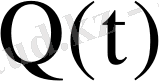 -ны былай жазуға болады:
-ны былай жазуға болады:
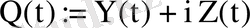 . Мұндағы
. Мұндағы
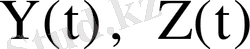 - нақты матрицалар. А матрицасы нақты болғандықтан
- нақты матрицалар. А матрицасы нақты болғандықтан
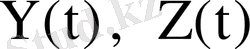 матрицалары өз алдарына (1) жүйенің матрицалық нақты шешімдері болып табылады. Олардың әрқайсысы (1) жүйенің
матрицалары өз алдарына (1) жүйенің матрицалық нақты шешімдері болып табылады. Олардың әрқайсысы (1) жүйенің
 нақты шешімдерінен тұрады. Нақты меншікті сандарға сәйкес шешімдер тек
нақты шешімдерінен тұрады. Нақты меншікті сандарға сәйкес шешімдер тек
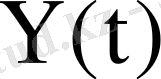 матрицасына ған кіреді.
матрицасына ған кіреді.
 матрицасында бұл шешімдер қай тік жолда тұрса,
матрицасында бұл шешімдер қай тік жолда тұрса,
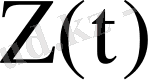 матрицасында сол номерлі тік жолда нольдік шешімдер тұрады. Ал комплекс мәнді меншікті сандарға сәйкес келетін шешімдердің нақты бөлігі
матрицасында сол номерлі тік жолда нольдік шешімдер тұрады. Ал комплекс мәнді меншікті сандарға сәйкес келетін шешімдердің нақты бөлігі
 -ге, ал жорамал бөлігі
-ге, ал жорамал бөлігі
 -ге кіреді. Бұл айтылғаннан жалпы жағдайда
-ге кіреді. Бұл айтылғаннан жалпы жағдайда
 не
не
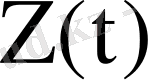 матрицаларына кіріп тұрған шешімдерді бәрі бірдей өзара сызықты тәуелсіз болмайтыны шығады. Яғни
матрицаларына кіріп тұрған шешімдерді бәрі бірдей өзара сызықты тәуелсіз болмайтыны шығады. Яғни
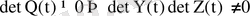 . Базисті құрайтын шешімдер саны
. Базисті құрайтын шешімдер саны
 болғандықтан
болғандықтан
 матрицаларын құрайтын нольдік емес
матрицаларын құрайтын нольдік емес
 шешімдерінің
шешімдерінің
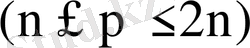 ішінде тек
ішінде тек
 шешім ғана өзара сызықты тәуелсіз болады. Олардан құрылған матрица
шешім ғана өзара сызықты тәуелсіз болады. Олардан құрылған матрица
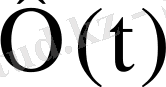 нақты фундаментальдық матрица болады да (1) жүйенің нақты жалпы шешімі
нақты фундаментальдық матрица болады да (1) жүйенің нақты жалпы шешімі
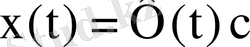 түрінде жазылады. Мұндағы
түрінде жазылады. Мұндағы
 -еркін тұрақты вектор.
-еркін тұрақты вектор.
Мысалдар. Төмендегі жүйелерді интегралдау керек.
1
0
.
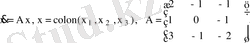 .
.
А матрицасының меншікті сандарын табу үшін
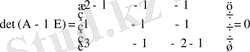
характеристикалық теңдеуін құрамыз. Анықтауышты ашсақ,
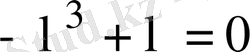
теңдеуі алынады. Сондықтан А матрицасының характеристикалық сандары
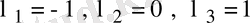 болады. Олар әртүрлі болғандықтан А матрицасының Жордан формасы ---
болады. Олар әртүрлі болғандықтан А матрицасының Жордан формасы ---
 .
.
А матрицасының
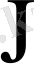 -ге келтіретін
-ге келтіретін
 матрицасын табалық.
матрицасын табалық.
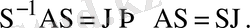
егер
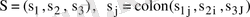 десек, онда
десек, онда

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz