Экономиканы талдаудың баланстық әдісі

Пән: Экономика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

ЭКОНОМИКАНЫ ТАЛДАУДЫҢ БАЛАНСТЫҚ ӘДІСІ

Салааралық баланстық модельдер макроэкономикалық талдаудың негізін құрайды. Бұл модельдер елдің экономикалық дамуының ең маңызды деген сапалық және құрылымдық сипаттарын болжамдау үшін қолданыла алады. Олардың негізінде салалардың арасындағы өзара байланыстарды жүйелі түрде талдау жүргізіледі, негізгі экономикалық пропорциялар анықталады. экономикадағы баға туындауының ерекшеліктері мен құрылымдық алға жылжулар қарастырылып, өндірістің экономикалық тиімділігі зерттеледі.

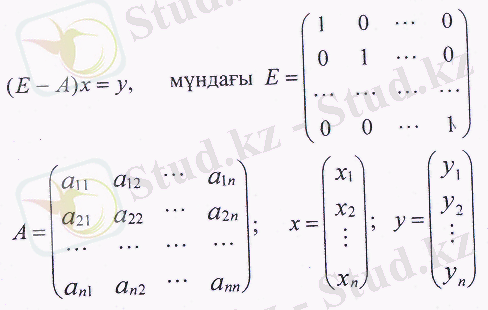
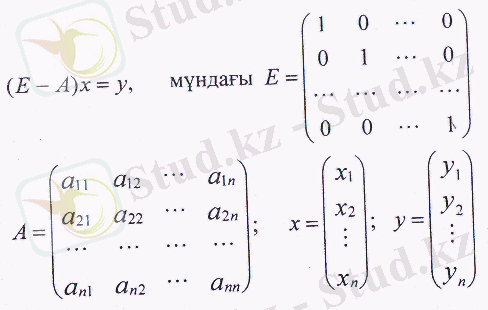
Өзара байланысты п саладан немесе өндірістен тұратын кейбір экономикалық жүйені қарастырайық. Әр сала өнімінің бір бөлігі жүйенің ішінде өндіріс құралдары, шикізат, жартылай фабрикаттар және т. б. ретінде қолданылады (өндірісішілік қолданыс), ал жекелей сыртқы қолданысқа жіберіледі (соңғы өнім) . Осылайша, зерттеліп отырған экономикалық жүйенің әрбір саласы немесе өндірісі, бір жағынан, өнімді өндіруші ретінде, екінші жағынан, оны тұтынушы ретінде көрінеді.

Тапсырманың берілуінің екі нұсқасы болуы мүмкін.

1. Жүйенің барлық салалары өндірісінің валдық деңгейлері берілген, әр саланың соңғы өнімінің көлемін анықтау қажет;

2. Жүйенің барлық салаларының соңғы өнімінің жоспар бойынша белгіленген деңгейі берілген, валдық өнімйің соңғы өнім бойынша құрылған тапсырмаларға да, өндірістің технологиялық құрылымына да негізделген сәйкес шамаларын анықтау қажет.

x _j арқылы - і-інші саланың валдық өндірісін, у _і арқылы оның соңғы өнімін белгілейміз (7 = 1, п ) .

Онда х, - у, і ~ інші саланың осы саланы коса алғанда жүйенің басқа салаларының тұтынуына, яғни өндірісішілік тұтынуға жіберілетін өнімнің бөлігін көрсетеді. х _і арқылы і-інші саланың j -інші сала тұтынатын өнімінің көлемін көрсетеді 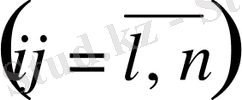Осы белгілеулерді ескере отырып, тапсырманың барлық берілгендерін кестеге орналастырамыз (36-кесте) .

36-кесте

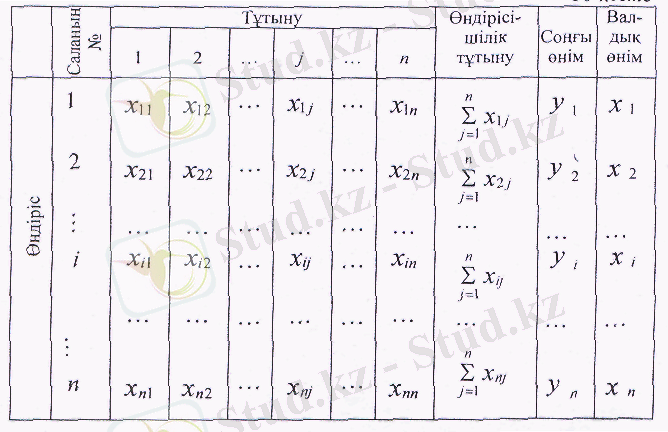
Көріп отырғанымыздай кестенің жолдарында орналасқан шамалар келесі баланстық теңдіктермен байланысты:

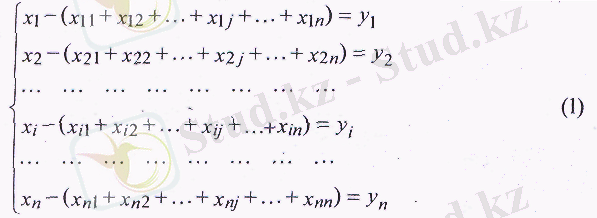
Осы кестені, сонымен қатар баланстық катынастарды (1) өткен кезеңнің экономикалық жүйесі үшін құруға болады. (Ары қарай жүйенің барлық өлшемдері ақшалай көрініс табу арқылы қарастырылады деген болжам жасауға болады) . Баланстық әдістердің тапсырмасы болып болашақтағы (жоспарланған) кезеңге арналған жүйенің негізгі өлшемдерін анықтау табылады. Алайда жүйе (I) берілген мәндер бойынша, мысалы, соңғы өнімді у _і (і- l , п), х, (i- l , n) салаларының валдық өнімдерінің көлемін анықтауға мүмкіндік бермейді, өйткені х _і белгісіздерінен басқа жүйе п ² x _ij белгісіздерін қамтиды, бұлар өз кезегінде х _i мәніне тәуелді.

Сондықтан жүйені (1) келесі түрде құрамыз. а _ij шамаларын енгіземіз, олар мына формула бойынша анықталады:

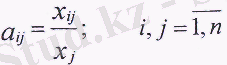(2)

Бұл шамалар тікелей шығындардың коэффициенті деп аталады. Олар і-інші сала өнімдерінің j-інші сала өнімдерінің бірліктерін өндіруге кеткен шығындарды анықтайды және ең бастысы j-інші саланың өндіріс технологиясына байланысты. Сондықтан бұл коэффициенттер технологиялық деп те аталады. Бұл коэффициенттер өткен уақытты да, болашақты да қамтитын уақыт кезеңінің ішінде еш өзгермейді деп санауға болады, яғни ол былайша көрініс табады:

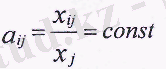(3)

Осыдан мынадай теңдік аламыз: х _ij = а _ij x _j (4)

(4) негізінде жүйе (1) мынадай түрге ие болады:

(5)

Жүйені (5) жинакталіан матрица түрінде жазамыз:

(6)

А матрицасын тікелей шығындар матрицасы, құрылымдық немесе технологиялық матрица деп атайды.

(6) жүйені шеше отырып, мына теңдікті аламыз:

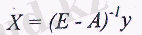(7)

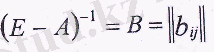деп белгілей отырып, (7) жүйені жазамыз:

X = By (8)

Осылайша, (6) және (8) желілік теңдіктер жүйесі зерттеліп отырған экономикалық жүйенің баланстық модельдерін білдіреді. Олар болашақ (жоспарланған) кезең үшін соңғы өнім векторын тудыра отырып, жүйе салаларының валдық өнімдерінің қажетті көлемдерін анықтауға мүмкіндік береді.

Сонымен қатар В матрицасының элементтері үлкен экономикалық мазмұнға ие. Шындығында, осы экономикалық жүйеде 1-саланың соңғы өнімінің бір бірлігі өндіріледі делік,

яғни: 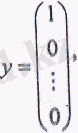онда у мәнін (8) жүйесіне қоя отырып, жүйе салаларының валдық өнімінің соңғы өнімнің осы бірліктерінің өндірілуін қамтамасыз ететін шамаларын аламыз:

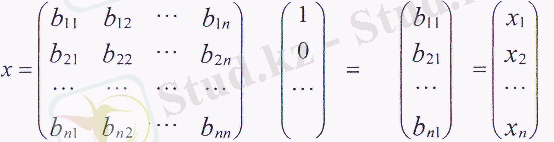
Осы жерден мынадай теңдіктер шығады: х ₁ =b ₁₁ , х ₂ = b ₂₁ , ., ., х _n = b _n1 , яғни 1-саланың соңғы өнімінің бір бірлігін өндіру үшін 1-сала өнімінің b ₂₁ бірлігін, 2-сала өнімінің бірлігін және n саласы өнімінің b _n1 бірлігін шығындау қажет.

Осы берілген экономикалық жүйеде 2-саланың соңғы өнімінің бір бірлігі, яғни 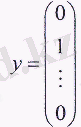өндіріледі делік. у-тің осы мәнін (8) жүйесіне қоя отырып, мына теңдікті аламыз:

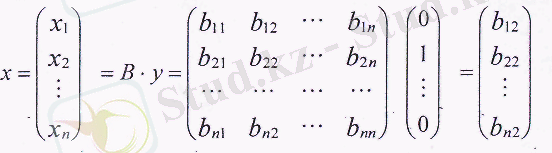
Бұдан шығатыны: x ₁ - b ₁₂ , х ₂ = b ₂₂ , …, x _n = b _п2 , яғни 2-саланың соңғы өнімінің бір бірлігін дайындау үшін 1-сала өнімінің b _j2 бірлігін, 2-сала өнімінің b ₂₂ бірлігін және п -сала өнімінің b _п2 бірлігін шығындаймыз, және соңында осыған ұқсас жолмен қарастыра отырып, бұл экономикалық жүйеде n-інші саланың соңғы өнімінің бір бірлігі өндіріледі деуімізге болады, яғни 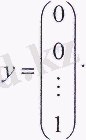у-тің осы мәнін (8) жүйесіне коя отырып, жүйеде п -інші саланың соңғы өнімінің бір бірлігін өндіру үшін 1-саланың b _1п бірлігін, 2-саланың b _2п бірлігін және п -інші саланың b _пп бірлігін шығындау қажет екендігін анықтаймыз,

Осылайша, В= (Е - А) ^-1 матрицасының элементтері қарастырылып отырған экономикалык жүйе салаларының осы жүйенің соңғы өнім бірліктерін өндіруге кеткен шығындарын көрсетеді және толық шығындар коэффициенті деп аталады. Олар тікелей шығындарды да, жанама шығындарды да камтиды.

Егер 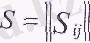арқылы жанама шығындар матрицасын белгілесек, онда 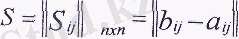пхп екендігі анықталады.

Жоғарыда айтылғандарды 2 өндірістік саладан тұратын келесі тапсырманы шешу барысында талқылаймыз:

37-кесте

Тұтыну: Тұтыну

Соңғыөнім:

Соңғы

өнім

Валдықөнім:

Валдық

өнім

: 1

Тұтыну: 2

: Өндіріс

Тұтыну: 1

Соңғыөнім: 100

Валдықөнім: 160

240

500

: 2

Тұтыну: 275

Соңғыөнім: 40

Валдықөнім: 85

400

Осы берілгендер бойынша тікелей шығындар коэффициенттерін есептеп шығарамыз:

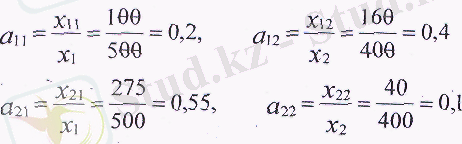
Тікелей шығындар матрицасы:

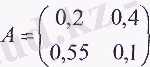
Онда желілік баланстық модель мынадай болады: (Е-А) х =у мынадай түрге ие болады:

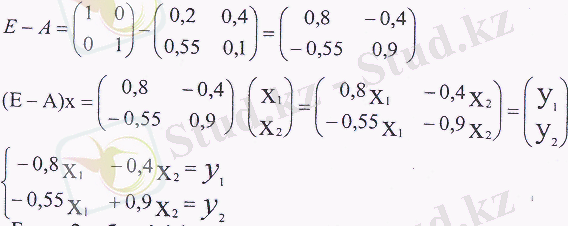
Бұл 2 белгісізі бар 2 теңдік жүйесі соңғы өнім құрылымындағы кез келген өзгерстің валдық өнімге әсерін зерттеу үшін соңғы өнімнің y ₁ , у ₂ берелген мәндері бойынша зерттеліп отырған х ₁ жэне x ₂ экономикалық жүйелері салаларының валдық өнімдерін анықтау үшін қолданыла алады.

Енді толық өндірісішілік шығындарды және 2-баланстық модельді анықтаймыз:

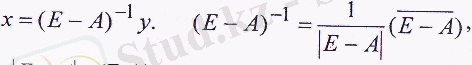
Мүндағы 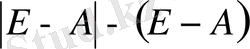матрицасынын анықтағышы.

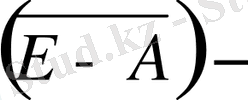біріккен матрица

Онда теңдік мынадай түрге ие болады:

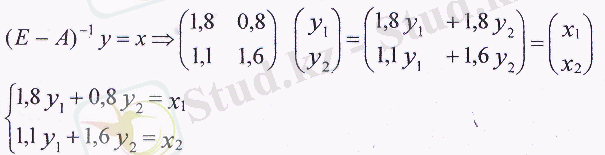
Бұл модельді валдық өнімнің зерттеліп отырған жүйенің соңғы өнімінің құрылымына әсерін талдау үшін қолдануға болады.

Толық шектеу әдісі арқылы қолданылатын қайта жасау үрдістерінің жиынтығы осы жүйе мен (Е - А) -1 мәнінің көбейтіндісіне тең, яғни

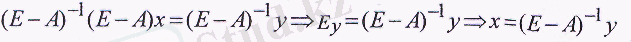
Кеңейтілген матрица түрін құрайық:

(Е-А у)

Енді толық шектеу әдісін осы матрицаға қолдансақ, мынадай теңдік аламыз:

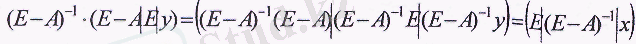
Осылайша, қайта жасаудың нэтижесінде (Е-А) матрицасының орнына -бірліктік матрица, ал бірліктік матрицаның орнына - (Е-А) ^-1 кері матрицасы, ал у векторының орнына х векторы келеді. Осы есептеулерді Гаусс кестесінде көрсету ыңғайлы. Алғашқы кестеде кеңейтілген матрицаны жазамыз.

Есептеулерді алдындағы мысал негізінде орналастырамыз.

38-кесте

Итерация №: Итерация №

Е-А: Е-А

Е: Е

V: V

Итерация №: 1

0, 8

-0, 55

Е-А:

-0, 4

0, 9

Е:

240

Итерация №: 2

Е-А:

: -0, 5 0, 625

Е: 1, 25 0, 6875

V: 0 1

300

250

Итерация №: 3

Е-А:

Е: 1, 8 1, 1

V: 0, 8 1, 6

500

400

Итерация №:

Е-А: Е

Е: (Е-А) ^-1

КҮНТІЗБЕЛІК ЖОСПАРЛАУДЫҢ ЖЕЛІЛІК ӘДІСІ

Желілік әдістер өзара баиланысты көптегеи жекелеген операциялардан тұратын өндірістік үрдістерді зерттеу барысында қолданыс табады. Бүкіл осы үрдістер кешені бір кемесе бірнеше мақсатқа жетуге негізделген, Өндірістік үрдіс технологиясы кешенінің барлық жұмыстары өзара былай байланысты: олардың әрқайсысына өзінің алдындағы жұмыстар, яғни өзі солардың нәтижесіне сүйенетін және осыған орай осы жұмыстың орындалуының басталуына дейін орындалуы тиіс жұмыстар тиесілі. Өз кезегінде, бұл жұмыс үрдістің осы жұмыс аяқталғаннан кейін ғана бастала алатын өзге жұмыстарының алдында келеді. Жеке операциялардың немесе жұмыстардың байланыстарын және олардың бүкіл жұмыс кешенін орындау барысындағы бірізділігін бейнелейтін график осылайша қалыптасады. Бұл график үрдістің желілік моделі деп аталады.

Желілік модельдің негізін желілік график - жұмыстар кешенінің бейнелік көрінісі құрайды. Желілік графиктің негізгі элементтері болып ЖАҒДАИ және ЖҰМЫС табылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.