Функцияның туындысы және дифференциалы: анықтамалар, геометриялық және механикалық мағыналар, теоремалар мен дифференциалдау ережелері


Тақырыбы: Функцияның туындысы және дифференциалы
Дәрістің мақсаты : Функцияның туындысын таба білу, туындының механикалық және геометриялық мағыналарын түсіну, күрделі функциялардың туындысын есептеуді үйренулері, жаңа ұғымдар және анықтауларды меңгерулері керек.
Бастапқы сөздер : Туындының анықтамасы, белгiлену түрлері. Есептеудiң мысалдары. Дифференциалдау ережелері. Күрделі функцияның туындысы. Кері функцияның туындысы. Туындылар таблицасы. Жоғарғы ретті туындылар. Лейбниц формуласы. Локальды экстремум. Ферма теоремасы. Ролль, Коши, Лагранж теоремалары. Дарбу теоремасы. Сызықты функция. Дифференциал.
Функцияның туындысы.
Туынды ұғымы өзара байланысты екені алдын ала көрінбейтін келесі екі есепті шығарғанда пайда болды - ол қисыққа жанама жүргізу және қозғалып бара жатқан дененің жылдамдығын табу есептері.
Жанама туралы есеп. ƒ функциясының графигін, яғни жазықтықта жатқан ( x , f ( x ) ) түріндегі нүктелер жиынын қарастырайық (оны y = f ( x ) қисығы не жай қисық деп те атайды) .
Белгілі бір ( x 0 , f ( x 0 ) ) нүктесінде қисыққа «тығыз орналасқан» түзуді сызу. Әрине, ондай түзу бар болса, онда ол тек қана сол қисыққа тән қасиеттер арқылы табылады. Сондықтан, қисықта жатқан басқа ( x 1 , f ( x 1 ) ) нүктесін алып, сол екі нүктеден түзу өткізейік. Оның теңдеуі
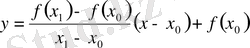
болады. Әрбір ( x 0 , f ( x 0 ) ) нүктесінен өтетін және y -тер осьіне паралель емес түзудің теңдеуі y = k ( x - x 0 ) + f ( x 0 ) түрінде жазылады, демек k нақты санына тәуелді болады.
Әрине, белгілі бір мағынада екі түзудің жақындығын оларды анықтайтын k сандарының жақындығы арқылы түсінуге болады. Ал, бізідң жағдайда сондай k сандары x 1 -ге мынадай тәуелділікте болады.
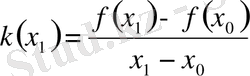
Сондықтан,
x
1
-ді
x
0
-ге ақырсыз жақын алған сайын,
k
(
x
1
) белгілі бір
k
санына ақырсыз жақындаса, онда теңдеуі
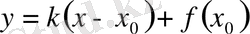 болатын түзуді бізге керекті «қисыққа тығыз орналасқан» түзу ретінде алуға болады.
болатын түзуді бізге керекті «қисыққа тығыз орналасқан» түзу ретінде алуға болады.
Мұндағы k -ны тапқан жолымыз шектер тілінде былай бейнеленеді.
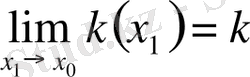 яғни
яғни
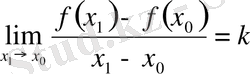 .
.
Айтқанымыздың геометриялық бейнесі 36-суретте берілген. Сонымен келесі анықтамаға келдік. Егер
 нүктесінде
нүктесінде
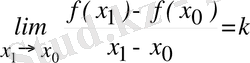 нақты мәнді шегі бар болса, онда
нақты мәнді шегі бар болса, онда
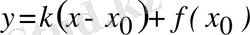 түзуі
түзуі
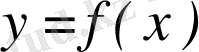 қисығының
қисығының
 нүктесіндегі жанамасы деп аталады.
нүктесіндегі жанамасы деп аталады.
Жылдамдық туралы есеп.
Материялық нүкте түзу бойымен белгілі бір бағытта қозғалып келе жатсын. Оның түзу бойындағы белгілі бір нүктеден
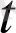 мезгіліндегі ара қашықтығы
мезгіліндегі ара қашықтығы
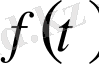 болсын.
болсын.
Әуелі
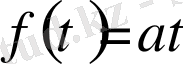 болсын, яғни нүкте бірқалыпты қозғалсын. Онда кез келген
болсын, яғни нүкте бірқалыпты қозғалсын. Онда кез келген
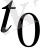 мен
мен
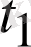 мезгілдері арасында нүкте
мезгілдері арасында нүкте
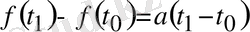 жолын жүреді, ал
жолын жүреді, ал
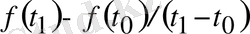 қатынасы сол қозғалыстың жолы деп аталады да, тұрақты болып,
а
санына тең болады.
қатынасы сол қозғалыстың жолы деп аталады да, тұрақты болып,
а
санына тең болады.
Егер нүктенің қозғалысы бірқалыпты болмаса, онда
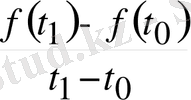 қатынасы тұрақты болмай
қатынасы тұрақты болмай
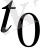 мен
мен
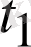 мезгілдеріне тәуелді болады. Ол
мезгілдеріне тәуелді болады. Ол
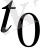 мен
мен
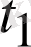 мезгілдері арасындағы материялық нүктенің орташа жылдамдығы деп аталады.
мезгілдері арасындағы материялық нүктенің орташа жылдамдығы деп аталады.
Расында, орташа жылдамдығы нүктенің
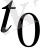 мен
мен
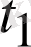 мезгілдері арасында қандай жылдамдықпен қозғалғаны туралы ешқандай әсер бермейді, өйткені ол бір мезгіл жылдам, бір мезгіл жай қозғалуы мүмкін. Орташа жылдамдық мағынасы мынада: егер нүкте сол арада бірқалыпты қозғалса, онда
мезгілдері арасында қандай жылдамдықпен қозғалғаны туралы ешқандай әсер бермейді, өйткені ол бір мезгіл жылдам, бір мезгіл жай қозғалуы мүмкін. Орташа жылдамдық мағынасы мынада: егер нүкте сол арада бірқалыпты қозғалса, онда
 мезгілінде
мезгілінде
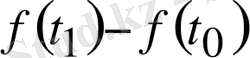 жолын жүру үшін оның жылдамдығы орташа жылдамдыққа тең болуы тиіс.
жолын жүру үшін оның жылдамдығы орташа жылдамдыққа тең болуы тиіс.
Егер
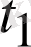 -ді
-ді
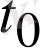 -ге ақырсыз жақындатқанда, оған сәйкес орташа жылдамдығы белгілі бір нақты санға ақырсыз жақындаса, онда сол санды
-ге ақырсыз жақындатқанда, оған сәйкес орташа жылдамдығы белгілі бір нақты санға ақырсыз жақындаса, онда сол санды
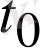 мезгіліндегі нүктенің жылдамдығы түрінде алған жөн.
мезгіліндегі нүктенің жылдамдығы түрінде алған жөн.
Сонымен, айтқанымызды шек арқылы бейнелесек, мына анықтамаға келеміз: егер
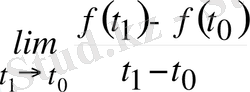
нақты мәнді шегі бар болса, онда оны
 тәртібі арқылы бейнеленген қозғалыстың
тәртібі арқылы бейнеленген қозғалыстың
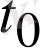 нүктесіндегі жылдамдығы деп атайды.
нүктесіндегі жылдамдығы деп атайды.
Айталық,
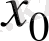 нүктесінде және оның төңірегінде
нүктесінде және оның төңірегінде
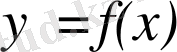 функциясы анықталған болсын.
функциясы анықталған болсын.
Анықтама.
Аргумент
 - тің
- тің
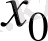 нүктедегі өсімшесі деп
нүктедегі өсімшесі деп
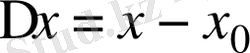 айырымын айтады
.
айырымын айтады
.
Анықтама.
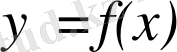 функциясының
функциясының
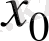 нүктедегі өсімшесі деп мына
нүктедегі өсімшесі деп мына
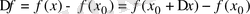
айырманы айтады
Бұл өсімше екі
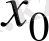 және
және
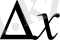 аргументтерге тәуелді. Геометриялық тұрғыда
аргументтерге тәуелді. Геометриялық тұрғыда
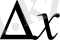 және
және
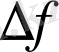 функция графигі бойымен
функция графигі бойымен
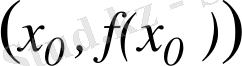 нүктеден
нүктеден
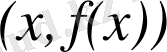 нүктеге дейін жылжығанда, нүктенің абсцисасы мен ординатасының өзгеруін көрсетеді.
нүктеге дейін жылжығанда, нүктенің абсцисасы мен ординатасының өзгеруін көрсетеді.
Мысалы, егер
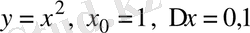 болса, онда
болса, онда
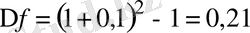 , яғни қабырғасы 1- ге тең шаршының қабырғасын 0, 1- ге арттырсақ, онда оның ауданы 0, 21- ге артады.
, яғни қабырғасы 1- ге тең шаршының қабырғасын 0, 1- ге арттырсақ, онда оның ауданы 0, 21- ге артады.
Анықтама.
Егер
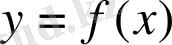 функциясы
функциясы
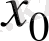 нүктенің төңірігінде анықталған және
нүктенің төңірігінде анықталған және
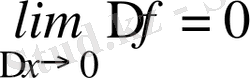 болса
,
онда ол
болса
,
онда ол
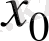 үзіліссіз деп аталады
.
үзіліссіз деп аталады
.
Шындығында да,
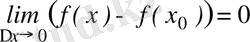

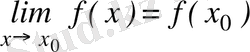 .
.
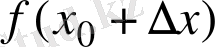 B
B
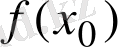 A
A

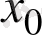
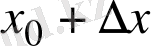
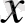
Анықтама.
Егер
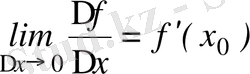 бар болса, онда бұл сан
бар болса, онда бұл сан
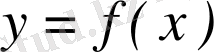 функциясының
функциясының
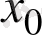 нүктедегі туындысы деп аталады
.
нүктедегі туындысы деп аталады
.
Бұл туынды мына символдардың бірімен белгіленеді:
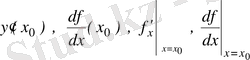 .
.
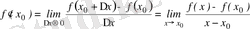 .
.
Анықтама.
Егер
 функциясы
функциясы
 нүктеде шекті туындыға ие болса, онда ол осы нүктеде дифференциалданады деп аталады.
нүктеде шекті туындыға ие болса, онда ол осы нүктеде дифференциалданады деп аталады.
Енді функцияның дифференциалымен оның үзіліссіздігінің арасындағы байланысты анықтайық, ол үшін бұл анықтамада
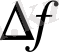 - ті ажыратамыз.
- ті ажыратамыз.
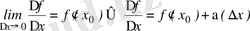 ,
,
Сондықтан
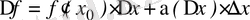 .
.
Теорема.
Егер
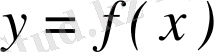 функциясының
функциясының
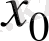 нүктеде дифференциалы бар болса
,
онда ол бұл нүктеде үзіліссіз болады
.
нүктеде дифференциалы бар болса
,
онда ол бұл нүктеде үзіліссіз болады
.
Кері тұжырым дұрыс емес, мысалы,
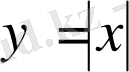 функциясы анықталу облысының барлық нүктелерінде үзіліссіз, бірақ ол
функциясы анықталу облысының барлық нүктелерінде үзіліссіз, бірақ ол
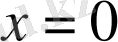 нүктесінде дифференциалданбайды, себебі
нүктесінде дифференциалданбайды, себебі
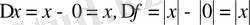 .
.
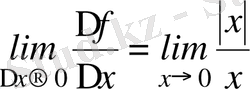 , ал бұл шек жоқ.
, ал бұл шек жоқ.
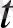 уақыт ішінде s(
t
) жол жүрген болсын.
уақыт ішінде s(
t
) жол жүрген болсын.
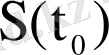
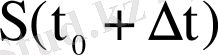
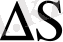
t уақыт ішінде жүрілген жол.
Онда
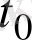 -ден
-ден
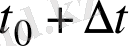 - ға дейінгі уақыт аралығында жүріп өткен жол
- ға дейінгі уақыт аралығында жүріп өткен жол
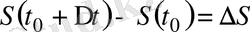 және
және
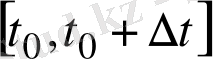 аралықтағы нүктенің орта жылдамдығы
аралықтағы нүктенің орта жылдамдығы
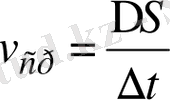 болады. Нүктенің
болады. Нүктенің
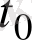 уақыт моментіндегі жылдамдығы
уақыт моментіндегі жылдамдығы
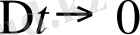
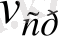 - дің шегі болады.
- дің шегі болады.
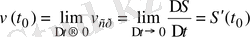 .
.
Демек, нүктенің
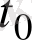 уақыт моментіндегі жылдамдығы жолдың
уақыт моментіндегі жылдамдығы жолдың
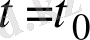 уақыттағы туындысы екен.
уақыттағы туындысы екен.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz