Механизм буындарының инерция күштерін анықтау

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

Тақырып: Механизм буындарының инерция күштерін анықтау. Кинематикалық тізбектердің статикалық анықталуы.

Мәселе және тәсілдер

Кинематикалық жұптардың элементтерін және буындарды беріктік шартына есептеу және олардың құрылымдық өлшемдерін анықтау үшін механизмнің қозғалысы кезінде оларға әсер ететін күштерді алдын - ала анықтайды.

Ереже бойынша, жетектегі буынға түсірілген күш, пайдалы кедергі күші берілді деп есептеледі. Механизмдердің кейбір буындары айнымалы қозғалыста және үдулерінің шамасы, бағыты айнымалы болады. Сондықтан, кинематикалық жұпта пайда болатын реакция күштері механизм буындарына түсірілген тек сыртқы күшке ғана емес, буындардың айнымалы қозғалысы кезінде пайда болатын қосымша динамикалық қысым күштеріне байланысты болады. Динамикалық қысым күштерінің шамасы және бағыты буындарының инерция күшіне тәуелді.

Сонымен, егер механизм буындарына, сыртқы күштерімен бірге оның буындарының инерция күшін қойса, онда механизмді тыныштықта болады деп қарастыруға болады. Бұл жағдайда кинематикалық жұп реакция күштерін анықтау үшін статика теңдеулерін пайдалануға болады. осы теңдеулерді шеше отырып қозғалыстағы механизмнің кинематикалық жұп қысым күштерін анықтаймыз.

Тепе - теңдік теңдеулер құрамына, механизмнің қозғалысы кезінде пайда болатын буындарының инерция күштері кіретін болатындықтан, мұндай есептеу тәсілі кинетостатикалық деп аталады.

Есептеу қысқа болу үшін кинематикалық жұп элементтерінің арасындағы үйкеліс күші есепке алынбайды. Бірінші кинематикалық жұп қысым күштерін анықтайды. Сонан соң, үйкеліс коэффициентін қабылдап, механизмдердің кинематикалық жұптары бойында пайда болатын үйкеліс күшін анықтайды. Кинетостатикалық есептеу қорытындысында механизмнің буындарына әсер ететін пайдалы кедергі және буындардың инерция күштері әсерінен бастапқы буынның реакция күшін анықтауға болады. Бұл күштің кривошиптің айналу өсіне қатысты моментіне тең момент М _қ , қозғаушы моментке тең.

Буындардың инерция күштері

Буынның материялық нүктелерінің инерция күштері бір нүктеге келтіріледі және олар негізгі вектор және негізгі момент деп аталады.

Буынның инерция күші деп аталатын инерция күшінің негізгі векторы мынадай формуламен анықталады:

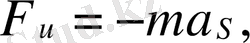(1)

мұндағы m [кг] - буын массасы, 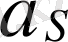[м⋅с ^{- 2} ] - буынның масса S центрінің үдеуі. Инерция күшінің бағыты 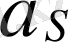векторының бағытына қарама - қарсы бағытталады. Оның өлшем бірлігі [кг⋅м⋅с ^{- 2} ], яғни ол нъютонмен өлшенеді [H] .

Буынның инерция күші

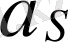
1 - сурет

Жазық параллель қозғалыстағы және оның қозғалыс жазықтығына параллель симметриялы жазықтығы бар буынды қарастырамыз. Инерция күштерінің келтіру центрі ретінде оның масса центрі алынады (1 - сурет) . Онда қос күш инерция момент шамасына тең инерция күштерінің негізгі моментінің өрнегі мынадай формуламен анықталады:

M _u = − I _S ⋅ε, (2)

мұндағы I _S [кг⋅м ² ] - буынның центрлік инерция моменті, ε [c ^{- 2} ] - буынның бұрыштық жылдамдығы.

Инерция моментінің өлшем бірлігі [кг⋅м⋅с ^{- 2} ] = [Н⋅м] . Әсер етуші жазықтығы буынның қозғалыс жазықтығына параллель, буынның бұрыштық үдеуі бағытына қарама - қарсы бағытталады.

Сонымен, жалпы жағдайда буынның инерция күштері S нүктесіне түсірілген бір инерция күшіне және бір инерция күшінің моментіне келтіріледі.

Буынның инерция күштерінің жеке жағдайлары

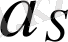
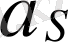
a )

b )

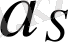
c ) d )

e ) f )

2 - сурет

Жеке жағдайлар (2 - сурет)

Буынның ілгерілемелі қозғалысы (2, а - сурет) . Инерция күштері бір инерция күшіне келтіріледі және (1) формуламен анықталады.

Буынның айнымалы айналмалы қозғалысы (2, б - сурет) . Инерция күштері күшіне және M _u инерция күшінің моментіне келтіріледі, (1) және (2) формулаларымен анықталады. Бұл жағдайда буынның масса центрінің толық үдеуі мынадай формуламен анықталады:

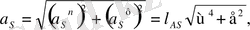(3)

мұндағы a _S ⁿ және a _S ^τ буынның масса центрінің нормаль және жанама құраушы үдеуі, ω и ε - буынның бұрыштық жылдамдығы және бұрыштық үдеуі, l _AS - S масса центрінен буынның А айналу өсіне дейінгі ара қашықтық.

Күш - ді және M _u - ді бір күшіне келтіруге болады. Бұл үшін күшін оның бағытын сақтай отырып, буынның тербеліс центрі K нүктесіне қоямыз (2, с - сурет) . Айналу өсі А - дан тербеліс центрі К - ға дейінгі ара - қашықтық мынадай теңдік арқылы анықталады:

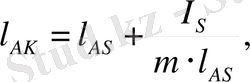Equation. 3 (4)

Буынның бірқалыпты айналмалы қозғалысы ( 2, d ) . Инерция күштері бір күшіне келтіріледі және AS түзуі бойымен буынның масса центрінің нормаль үдеу векторы бағытына қарсы бағытталады, шамасы:

a _S ⁿ = ω ² ⋅ l _AS , (5)

және центріне тартқыш инерция күші мынадай формуламен анықталады:

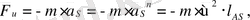(6)

Көбейтінді m l _AS теңгерілмегендік деп аталады және өлшем бірлігі [кг⋅м] .

Буынның масса центрі S оның айналу центрі А - мен беттескен жағдайдағы айнымалы айналмалы қозғалысы (2, е - сурет) . Буынның инерция күштері (2) формуламен анықталатын M _u инерция моментіне келтіріледі.

Буынның масса центрі S оның айналу центрі А - мен беттескен жағдайдағы бірқалыпты айналмалы қозғалысы (2, f - сурет) .

Бұл жағдайда l _AS = 0 және (3) формула бойынша a _S = 0, яғни = 0, және ε = 0 болғандықтан, M _u = 0. Инерция күші және инерция моменті нөлге болса, онда ол теңгерілген деп аталады.

Қандай да бір механизмнің берілген орнында барлық буындарының инерция күштерін анықтау үшін, жылдамдықтар және үдеулер жобасын тұрғызу қажет.

Құрылымдық топтың статикалық анықталуы

Төменгі кинематикалық жұп элементтері арасындағы қысым күшінің тең әсер етуші күші шамасымен, бағытымен және қойылу нүктесімен анықталады. Егер үйкеліс күшін есепке алмаса, онда айналмалы жұпта барлық уақытта күшінің қойылу нүктесі, ал ілгерілемелі жұпта оның бағыты белгілі (бағыттаушы түзуіне перпендикуляр) (3 - сурет) .