Коэффициенттері тұрақты және айнымалы ретті жай сызықтық дифференциалдық теңдеулерді Лаплас түрлендіруі мен операциялық әдістер арқылы шешу


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 49 бет
Таңдаулыға:
МАЗМҰНЫ
КІРІСПЕ . . . 3
1 СЫЗЫҚТЫ ЖАЙ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР
1. 1 Коэффициенттері тұрақты
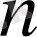 - ретті сызықты
- ретті сызықты
біртекті дифференциалдық теңдеулер
1. 2 Коэффициенттері тұрақты
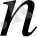 - ретті сызықты
- ретті сызықты
бейбіртекті дифференциалдық теңдеулер
1. 3 Коэффициенттері айнымалы сызықты
дифференциалдық теңдеулер
2 ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ
ЛАПЛАС ТҮРЛЕНДІРУІ АРҚЫЛЫ ШЕШУ
2. 1 Лаплас түрлендіруі және оның қасиеттері
2. 2 Лаплас түрлендіруі арқылы ізделінді функцияны анықтау
2. 3 Сызықты дифференциалдық теңдеулерді операциялық
тәсілдермен интегралдау
2. 3. 1 Бейбіртекті оң жағы жалған көпмүшелік коэффициенттері
тұрақты сызықты дифференциалдық теңдеу
2. 3. 2 Бейбіртекті оң жағы үздіксіз функциялы коэффициенттері
тұрақты сызықты дифференциалдық теңдеу
2. 3. 3. Бейбіртекті оң жағы үзілісті функциялы коэффициенттері
тұрақты сызықты дифференциалдық теңдеу
2. 4 Сызықтық дифференциалдық теңдеуді Дюамель
интегралын пайдаланып шешу
ҚОРЫТЫНДЫ . . .
ПАЙДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ . . .
КІРІСПЕ
Тақырыптың өзектілігі. Қазіргі кезде ғылыми - техникалық прогресс математикалық әдістердің ғылым мен техниканың барлық салаларына қарқындап енуімен сипатталады. Бұл прогресстің басталуы мен жүруі табиғатта болып жатқан құбылыстардың математикалық модельдерін жасаумен тығыз байланысты және ғылыми - техникалық прогресс үшін маңызы зор. Жалпы жағдайда жүріп жатқан процестер мен құбылыстарды, олардың табиғатының өте күрделілігіне байланысты, математиканың аппаратын пайдаланып, математика тіліне аудару оңай мәселе емес. Ғылым мен техниканың әр түрлі салаларында математикалық әдістерді нәтижелі қолдана білу үшін нақты практикалық есептерге осы әдістерді қолданудың негізгі принциптері жөнінде жеткілікті дәрежеде түсінік болуы қажет.
Ғылым мен техникада көптеген есептер, функциялар, алгебралық, дифференциалдық немесе интегралдық теңдеулер арқылы математика тiлiнде сипатталып жазылады. Мұндай есептер түрлiше жолдармен шешiледi. Аналитикалық әдiстер сондай жолдардың бiрi болып табылады.
Теориялық сұрақтар мен қолданбалы есептердің аналитикалық зерттеулерінің тиімді аппаратының бірі - операциялық есептеулер. Операциялық есептеу математикалық талдаудың маңызды бір саласы болып табылады. Механика, математика және техника есептерін шешуде операторлық әдістер жиі қолданылады. Жылу өткізгіштік теориясында, электротехника және радиотехника, электр тізбегіндегі тұрақты емес құбылыстарды, автоматты реттегіштер жүйесінің жұмысын зерттеуде, сонымен қатар сызықтық дифференциалдық және интегралдық, айырымдық теңдеулер теориясында операциялық есептеу әдістері кеңінен пайдаланылады. Оператор, операция сөздері латын тілінде operor-жасаймын, operator-жасаушы, жұмыскер деген ұғымды білдіреді. Ал operatio-амал, қимыл, жұмыс, енгізу, іске асыру ұғымдарына сәйкес келеді[1] .
Операциялық есептеу саласындағы алғашқы ғылыми жұмыстар белгілерді есептеу, белгілеулер енгізу арқылы есептеу деген сияқты атаулармен басталады. Операциялық әдістерді физикалық және техникалық есептерді шешу үшін қолдану ағылшын ғалымы Хевисайдтың 1892 жылы жарияланған еңбектерінен кейін басталған[2] .
Операциялық есептеудің алғашқы математикалық түрде негізді дәлелденуі ағылшын математигі Бромвичтің (1916), америка инженері Карсонның (1926) және голландия инженер-электригі Ван дер Польдің (1929-1932) еңбектерімен тығыз байланысты. Операциялық есептеулерді зерттеулерде орыс және совет ғалымдары өте зор үлес қосты. Россияда бұл саладағы алғашқы еңбектердің бірі М. Е. Ващенко-Захарченконың 1862 жылы шыққан «Сызықты дифференциалдық теңдеулерді интегралдаудың қолданылуы және символикалық есептеулері» атты монографиясы болып табылады. Бұл монографияда символикалық есептеулердің мазмұны толық ашылып көрсетілген, сонымен бірге сызықты коэффициенттері тұрақты және айнымалы дифференциалдық теңдеулердің шешімін табуға қалай қолдану керектігі көрсетілген. Сонымен қатар, операциялық есептеулердің ең негізгі формуласы беріліп, ол қазіргі уақытта есептің шешімін табудың негізгі класын кеңейтуге мүмкіндік береді.
Сонымен қатар, операциялық есептеу теориясын дамытуда орыс ғалымдары Лурье А. И., Данилевский А. Н., Эфрос А. М., Конторович М. И., [3] Диткин В. А. [1] айтарлықтай үлес қосты.
Ғылыми зерттеулер нәтижесінде операциялық есептеу теориясында Лаплас бойынша түрлендірілетін функцияларды ғана пайдалану, оның қолданылу өрісін тарылтатындығы байқалды. Бұл кемшіліктен құтылу үшін Хевисайдтың белгілеулеріне қайта оралып, функция ұғымын жалпылау қажеттігі туды. Осындай қажеттілікпен байланысты жарыққа шыққан польша математигі Я. Микусинскийдің «Операциялық есептеу» деп аталатын еңбегі алғашқы операциялық көзқарасқа қайта оралудың бастамасы болды.
Операциялық әдістің мәнін қысқаша былай сипаттауға болады:
Нақты айнымалы
t
-ның
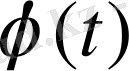 функциясы берілсін дейік. Бұл функцияның Лаплас түрлендіруі (
функциясы берілсін дейік. Бұл функцияның Лаплас түрлендіруі (
 -түрлендіру) мына түрде болсын
-түрлендіру) мына түрде болсын
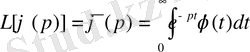
Бұл теңдіктің оң жағындағы жинақталатын меншіксіз интеграл.
 түрлендіруін пайдаланып, әрбір Лаплас бойынша түрлендірілетін түпнұсқа деп аталатын
түрлендіруін пайдаланып, әрбір Лаплас бойынша түрлендірілетін түпнұсқа деп аталатын
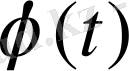 функциясына оның бейнесі деп аталатын комплекс айнымалының
функциясына оның бейнесі деп аталатын комплекс айнымалының
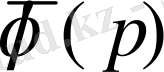 функциясын сәйкес келтіруге болады.
функциясын сәйкес келтіруге болады.
Лаплас түрлендіруінің тамаша қасиеттері бар. Мысалы,
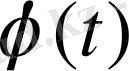 түпнұсқасын
түпнұсқасын
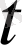 бойынша дифференциалдауға
бойынша дифференциалдауға
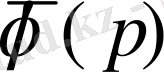 функциясын
р
комплекс айнымалысына көбейту амалы сәйкес келеді. Сонымен, түпнұсқаны дифференциалдау және интегралдау амалдарына бейнелер кеңістігінде қарапайым алгебралық амалдар, яғни
функциясын
р
комплекс айнымалысына көбейту амалы сәйкес келеді. Сонымен, түпнұсқаны дифференциалдау және интегралдау амалдарына бейнелер кеңістігінде қарапайым алгебралық амалдар, яғни
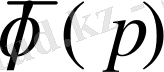 бейнесін
р
санына көбейту және бөлу амалдары сәйкес келеді.
бейнесін
р
санына көбейту және бөлу амалдары сәйкес келеді.
Берілген
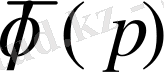 бейнесі бойынша оған сәйкес
бейнесі бойынша оған сәйкес
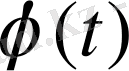 түпнұсқасын табу үшін Лапластың кері түрлендіруін (
түпнұсқасын табу үшін Лапластың кері түрлендіруін (
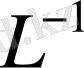 түрлендіру) пайдалануға болады.
түрлендіру) пайдалануға болады.
Дипломдық жұмыстың мақсаты.
Коэффициенттері тұрақты және айнымалы
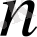 - ретті сызықты дифференциалдық теңдеулердің шешімін табуға операциялық есептеулерді, атап айтқанда Лаплас түрлендіруін қолдану болып табылады. Операциялық есептеулердің ерекшеліктерін зерттеу.
- ретті сызықты дифференциалдық теңдеулердің шешімін табуға операциялық есептеулерді, атап айтқанда Лаплас түрлендіруін қолдану болып табылады. Операциялық есептеулердің ерекшеліктерін зерттеу.
Дипломдық жұмыстың міндеттері.
- Жай дифференциалдық теңдеулерді операциялық есептеулерді пайдаланып шешу, Лаплас түрлендіруін пайдалану;
- Операциялық есептеулердің, атап айтқанда Лаплас түрлендіруінің ерекшеліктерін зерттеу.
Зетттеудің нысаны. Зерттеудің негізгі нысаны дифференциалдық теңдеулерді, оның ішінде жай дифференциалдық теңдеуге операциялық есептеулерді пайдаланып, берілген теңдеудің шешімін зерттеу болып табылады.
Зерттеу пәні. Зерттеудің негізгі пәні операциялық есептеулер мен дифференциалдық теңдеулер болып табылады.
Дипломдық жұмыстың ғылыми жаңашылдығы. Жұмыста бейбіртекті оң жағы рационал көпмүшелік, үздіксіз функция және үзілісті функциялы болғандағы коэффициенттері тұрақты сызықты дифференциалдық теңдеулердің шешімін операциялық есептеулер көмегімен, атап айтқанда Лаплас түрлендіруін пайдаланып табу қарастырылған. Сонымен бірге, Дюамель интегралын қолданып, сызықты дифференциалдық теңдеудің шешімі анықталған.
Зерттеу әдістемесі. Жай дифференциалдық теңдеулерді операциялық есептеулер көмегімен шешудің бірі - Лаплас түрлендіруі қарастырылады.
Дипломдық жұмыстың құрылымы. Жұмыс кіріспе, екі бөлім, қортынды және пайдаланылған әдебиеттер тізімінен тұрады.
Кіріспеде алдынғы ғылыми жұмыстарға шолу жасалынған, сонымен қатар осы дипломдық жұмыстың тақырыбының өзектілігі, маңыздылығы, мақсаты, зерттеу міндеттері мен нәтижелерінен шыққан жаңалықтар көрсетілген. Дипломдық жұмыстың қысқаша баяндалу мазмұны келтірілген.
Бірінші бөлімде - жай дифференциалдық теңдеулердің кейбір фактілері мен тұжырымдары және көмекші нәтижелер келтірілген. Оларға ортақ мысалдар қарастырылған.
Екінші бөлімде - Коэффициенттері тұрақты және айнымалы
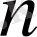 - ретті сызықты дифференциалдық теңдеулердің шешімін табуға операциялық есептеулерді, атап айтқанда Лаплас түрлендіруі арқылы шешу қарастырылған және мысалдар келтірілген.
- ретті сызықты дифференциалдық теңдеулердің шешімін табуға операциялық есептеулерді, атап айтқанда Лаплас түрлендіруі арқылы шешу қарастырылған және мысалдар келтірілген.
Жұмыстың қорытындысында тұтас зерттеудің тұжырымдары көрсетілген.
Дипломдық жұмыстың қысқаша мазмұны.
Бірінші бөлімде коэффициенттері тұрақты
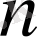 - ретті сызықты біртекті, бейбіртекті дифференциалдық теңдеулер және коэффициенттері айнымалы дифференциалдық теңдеулер туралы мәліметтер келтірілген.
- ретті сызықты біртекті, бейбіртекті дифференциалдық теңдеулер және коэффициенттері айнымалы дифференциалдық теңдеулер туралы мәліметтер келтірілген.
Екінші бөлім дифференциалдық теңдеулерді шешуде операциялық есептеулерді қолдануға арналған. Бұл бөлімде Лаплас түрлендіруі және оның қасиеттері, Лаплас түрлендіруі арқылы ізделінді функцияны анықтау, бейбіртекті оң жағы жалған көпмүшелік, үздіксіз функция және үзілісті функция болған жағдайдағы коэффициенттері тұрақты сызықты дифференциалдық теңдеулердің шешімін Лаплас түрлендіруі көмегімен табу және сызықты дифференциалдық теңдеулерді Дюамель интегралын пайдкаланып шешу қарастырылған.
1 СЫЗЫҚТЫ ЖАЙ ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕР
- Коэффициенттері тұрақты- ретті сызықты біртекті
дифференциалдық теңдеулер
Жай дифференциалдық теңдеулер көмегімен материалды нүктелерге қатысты қозғалыс жүйесі, химиялық кинетика, электрлік шынжыр, материалдардың қарсыласуы сияқты есептерді шешуге болады [7] .
Жай дифференциалдық теңдеулер үшін негізгі үш типті есеп бар: Коши есебі, шектік есептер және өзіндік мәні бар есептер[8] .
Жай дифференциалдық теңдеулерді шешудің үш тобы бар: дәл, сандық және жуықтау әдістері.
Дәл әдіс (аналитикалық) - ке дифференциалдық теңдеулерлерді элементар функциялар арқылы шешу жатады. Бұл әдістер жай дифференциалдық теңдеулер курсында оқытылады. Алайда, теңдеулер класы үшін құрастырылған нақты әдістер практикалық есептердің аз ғана бөлігін қамтиды.
Жуықтау әдісі
. Бұл
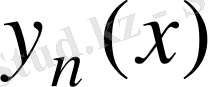 -тің шегі
-тің шегі
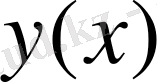 болатын және
болатын және
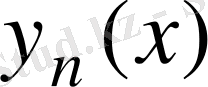 элементар функциялар немесе квадратуралар арқылы сипатталатын әдіс. Шекаралық есептің шешімін табудың жуықтау әдісі есептеу машиналарының пайда болуынан кейін дамыған.
элементар функциялар немесе квадратуралар арқылы сипатталатын әдіс. Шекаралық есептің шешімін табудың жуықтау әдісі есептеу машиналарының пайда болуынан кейін дамыған.
Сандық әдістер
- ізделініп жатқан
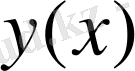 шешімнің жуық мәнін әйтеуір бір тордағы
шешімнің жуық мәнін әйтеуір бір тордағы
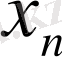 аргументінің мәні деп айтуға болады. Шешім кесте түрінде беріледі. Сандық әдістер
аргументінің мәні деп айтуға болады. Шешім кесте түрінде беріледі. Сандық әдістер
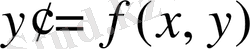
теңдеуінің немесе теңдеулер жүйесінің жалпы шешімін таба алмайды, олар дербес шешімді таба алады. Мысалы, Коши есебін шешу. Алайда, бұл есеп барлық теңдеулер класына қолданылады [9] .
Коэффициенттері тұрақты сызықты дифференциалдық теңдеулер алгебралық амалдар көмегімен түбіне дейін шешілетін кәдімгі дифференциалдық теңдеулердің қомақты, маңызды саласы болады.
 (1. 1)
(1. 1)
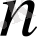 - ретті сықықты біртекті дифференциалдық теңдеу, мұнда
- ретті сықықты біртекті дифференциалдық теңдеу, мұнда
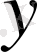 - тәуелсіз айнымалы
- тәуелсіз айнымалы
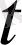 -ға байланысты белгісіз функция,
-ға байланысты белгісіз функция,
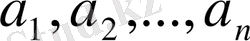 - тұрақты коэффициенттер.
- тұрақты коэффициенттер.
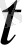 бойынша дифференциалдау амалын
бойынша дифференциалдау амалын
 арқылы белгілесек, онда
арқылы белгілесек, онда
 . Осындай белгілеме көмегімен (1. 1) теңдеуді мына түрге
. Осындай белгілеме көмегімен (1. 1) теңдеуді мына түрге
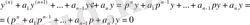
келтіруге болады, немесе,
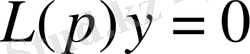 , мұнда
, мұнда
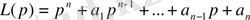 .
.
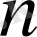 - ретті операторлық
- ретті операторлық
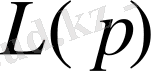 көпмүшеліктің
көпмүшеліктің
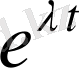 функциясына әсері мынадай:
функциясына әсері мынадай:
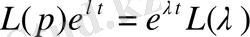 .
.
Егер
 , онда
, онда
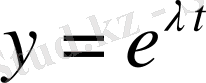 функциясы (1. 1) теңдеудің шешімі болады.
функциясы (1. 1) теңдеудің шешімі болады.
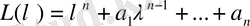 (1. 2)
(1. 2)
теңдеуі (1. 1) теңдеудің сипаттауыш теңдеуі, ал оның түбірлері теңдеудің сипаттауыш сандары деп аталады.
Егер сипаттауыш теңдеу түбірлері өзара жәй, яғни (1. 2)
 теңдеу көп еселі түбірлерге ие болмасын деп, оның түбірлерін
теңдеу көп еселі түбірлерге ие болмасын деп, оның түбірлерін
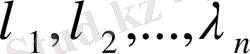 деп белгілейік. Онда
деп белгілейік. Онда
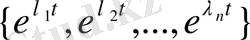 функциялар жүйесі (1. 1) теңдеудің сызықты тәуелсіз шешімдер жүйесі болады.
функциялар жүйесі (1. 1) теңдеудің сызықты тәуелсіз шешімдер жүйесі болады.
Анықтама.
(1. 1) теңдеудің
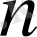 сызықты тәуелсіз шешімдер
сызықты тәуелсіз шешімдер
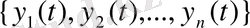 жүйесі сол теңдеу шешімдерінің өзек жүйесі деп аталады. Шешімдердің өзек жүйесі көмегімен (1. 1) теңдеудің жалпы шешімі мына түрде
жүйесі сол теңдеу шешімдерінің өзек жүйесі деп аталады. Шешімдердің өзек жүйесі көмегімен (1. 1) теңдеудің жалпы шешімі мына түрде

жазылады, ал сипаттауыш сандар әр түрлі болса, онда
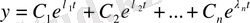
(1. 1) теңдеудің жалпы шешімі болады. (1. 1) теңдеудің күллі коэффициенттері нақты сандар болсын, онда сипаттауыш теңдеудің жорамал түбірлері қосарланып жүреді, яғни
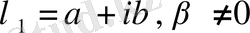 сипаттауыш сан болса,
сипаттауыш сан болса,
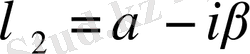 сипаттауыш сан болады. Осы қос түбірге
сипаттауыш сан болады. Осы қос түбірге
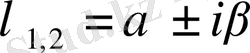 сәйкес келетін шешімдер мыналар
сәйкес келетін шешімдер мыналар
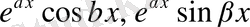
 саны сипаттауыш теңдеудің
саны сипаттауыш теңдеудің

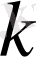 еселі түбірі болсын делік, яғни
еселі түбірі болсын делік, яғни

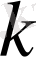 еселі
еселі
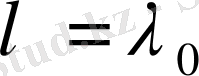 түбірге теңдеудің
түбірге теңдеудің
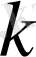 шешімі сәйкес келеді:
шешімі сәйкес келеді:
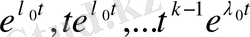 .
.
- Коэффициенттері тұрақты- ретті сызықты бейбіртекті
дифференциалдық теңдеулер
а) Коэффициенттері тұрақты
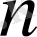 - ретті сызықты бейбіртекті дифференциалдық теңдеу
- ретті сызықты бейбіртекті дифференциалдық теңдеу
 (1. 3)
(1. 3)
берілсе, онда сызықты біртекті теңдеу
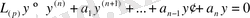 (1. 1)
(1. 1)
оған сәйкес біртекті теңдеу болады.
Егер
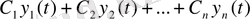 (1. 1) теңдеудің жалпы шешімі, ал
(1. 1) теңдеудің жалпы шешімі, ал
 (1. 3) теңдеудің дербес шешімі болса, онда (1. 3) теңдеудің жалпы шешімі мына түрде
(1. 3) теңдеудің дербес шешімі болса, онда (1. 3) теңдеудің жалпы шешімі мына түрде
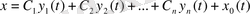 жазылады, яғни сызықты бейбіртекті теңдеудің жалпы шешімі сол теңдеудің дербес шешіміне оған сәйкес біртекті теңдеудің жалпы шешімін қосқанға тең болады.
жазылады, яғни сызықты бейбіртекті теңдеудің жалпы шешімі сол теңдеудің дербес шешіміне оған сәйкес біртекті теңдеудің жалпы шешімін қосқанға тең болады.
(1. 3) теңдеудің оң жағында тұрған
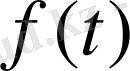 функциясы (бос мүше) жалған көпмүшелік деп аталатын арнайы түрде берілген функция болса, онда ол теңдеудің дербес шешімін
функциясы (бос мүше) жалған көпмүшелік деп аталатын арнайы түрде берілген функция болса, онда ол теңдеудің дербес шешімін
 табу жолы жалпы жағдайға қарағанда оңайлана түседі.
табу жолы жалпы жағдайға қарағанда оңайлана түседі.
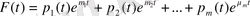
түрінде жазылған кез келген функция, мұнда
 - алгебралық көпмүшеліктер,
- алгебралық көпмүшеліктер,
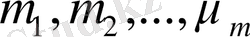 - қайсыбір комплекс сандар, жалған көпмүшелік деп аталады. Коэффициенттері тұрақты сызықты біртекті дифференциалдық теңдеудің әрбір жалған көпмүшелік қайсыбір коэффициенттері тұрақты сызықты біртекті теңдеудің шешімі болады.
- қайсыбір комплекс сандар, жалған көпмүшелік деп аталады. Коэффициенттері тұрақты сызықты біртекті дифференциалдық теңдеудің әрбір жалған көпмүшелік қайсыбір коэффициенттері тұрақты сызықты біртекті теңдеудің шешімі болады.
Теорема. Бейбіртекті теңдеу берілсін делік.
 , (1. 4)
, (1. 4)
Мұнда
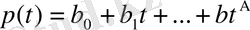 -
-
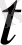 бойынша
бойынша
 дәрежелі көпмүшелік болсын,
дәрежелі көпмүшелік болсын,
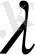 - комплекс сан. Айталық,
- комплекс сан. Айталық,
 , егер
, егер
 , ал
, ал
 болғанда
болғанда
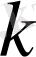
 түбірінің еселігі болсын. Онда (1. 4) теңдеудің
түбірінің еселігі болсын. Онда (1. 4) теңдеудің
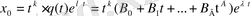 (1. 5)
(1. 5)
түрінде жазылатын шешім бар болады, мұнда
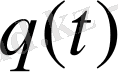
 дәрежелі көпмүшелік, оның коэффициенттерін анықталмаған коэффициенттер тәсілімен табуға болады.
дәрежелі көпмүшелік, оның коэффициенттерін анықталмаған коэффициенттер тәсілімен табуға болады.
Ескерту.
Егер комплекс сандар
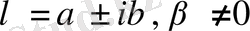 сипаттауыш теңдеудің
сипаттауыш теңдеудің

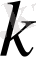 еселі түбірлері болса
еселі түбірлері болса
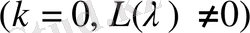 , ал (1. 4) теңдеудің оң жағы
, ал (1. 4) теңдеудің оң жағы
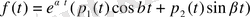 , мұнда
, мұнда
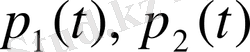 - алгебралық көпмүшеліктер, онда (1. 4) теңдеудің шешімі мына түрде ізделінеді.
- алгебралық көпмүшеліктер, онда (1. 4) теңдеудің шешімі мына түрде ізделінеді.
 ,
,
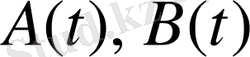 - дәрежесі
- дәрежесі
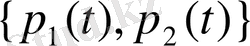 көпмүшеліктердің ең үлкен дәрежесіне тең алгебралық көпмүшеліктер.
көпмүшеліктердің ең үлкен дәрежесіне тең алгебралық көпмүшеліктер.
б) коэффициенттері тұрақты сызықты дифференциалдық теңдеудің
 (1. 3)
(1. 3)
босмүшесі
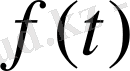 жалған көпмүшелік болмаса, онда (1. 3) теңдеудің дербес шешімін табу үшін тұрақты шамаларды вариациялау әдісі қолданылады. Осы әдіске тоқталайық. (1. 3) -ке сәйкес (1. 1) теңдеудің жалпы шешімі
жалған көпмүшелік болмаса, онда (1. 3) теңдеудің дербес шешімін табу үшін тұрақты шамаларды вариациялау әдісі қолданылады. Осы әдіске тоқталайық. (1. 3) -ке сәйкес (1. 1) теңдеудің жалпы шешімі
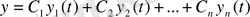 (1. 4)
(1. 4)
құрылсын делік. (1. 3) теңдеудің шешімін мына түрде
 (1. 5)
(1. 5)
іздейміз, мұнда
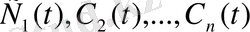 -
-
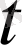 -дан тәуелді әзірге белгісіз функциялар.
-дан тәуелді әзірге белгісіз функциялар.
Осы функциялар төмендегі жүйеден
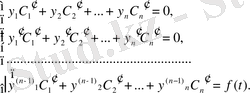 (1. 6)
(1. 6)
анықталады. Жүйені
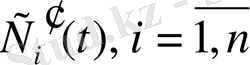 бойынша шешеміз.
бойынша шешеміз.

осыдан
 . Табылған
. Табылған
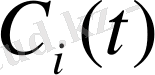 мәндерін (1. 5) -ке қоямыз, сонда
мәндерін (1. 5) -ке қоямыз, сонда
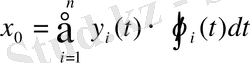 (1. 3) теңдеудің дербес шешімі болады.
(1. 3) теңдеудің дербес шешімі болады.
- Коэффициенттері айнымалы сызықты
дифференциалдық теңдеулер
а)
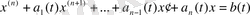 (1. 7)
(1. 7)
бейбіртекті сызықты теңдеу,
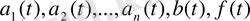 -
-
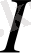 аралығында үздіксіз функциялар.
аралығында үздіксіз функциялар.
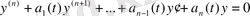 (1. 8)
(1. 8)
(1. 7) сәйкес біртекті сызықты теңдеу.
Егер
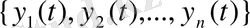 (1. 8) теңдеу шешімдерінің өзек жүйесі, ал
(1. 8) теңдеу шешімдерінің өзек жүйесі, ал
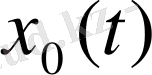 - (1. 7) -дің дербес шешімі болса, онда (1. 7) -дің жалпы шешімі мына түрде:
- (1. 7) -дің дербес шешімі болса, онда (1. 7) -дің жалпы шешімі мына түрде:
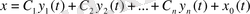
жазылады, яғни бейбіртекті сызықты теңдеудің жалпы шешімі оған сәйкес біртекті сызықты теңдеудің жалпы шешіміне өзінің қайсыбір дербес шешімін қосқанға тең.
Егер (1. 8) -нің дербес шешімі
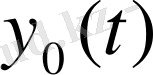 белгілі болса, оның ретін бірге төмендетіп,
белгілі болса, оның ретін бірге төмендетіп,
 - ретті сызықты дифференциалдық теңдеуге келтіруге болады. Ол үшін
- ретті сызықты дифференциалдық теңдеуге келтіруге болады. Ол үшін
 , (1. 8) теңдеуге қойғаннан кейін,
, (1. 8) теңдеуге қойғаннан кейін,
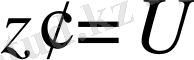 алмастыруы арқасында теңдеудің реті төмендетіледі.
алмастыруы арқасында теңдеудің реті төмендетіледі.
Егер (1. 8) -нің шешімдерінің өзек жүйесі белгілі болса, онда (1. 7) -дің дербес шешімі тұрақтыларды вариациялау әдісімен (Лагранж тәсілі) табуға болады.
(1. 8) -нің жалпы шешімі белгілі болсын,
 кез келген тұрақты шамалар. (1. 7) -дің дербес шешімін мына түрде
кез келген тұрақты шамалар. (1. 7) -дің дербес шешімін мына түрде
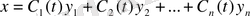 іздейміз, мұнда
іздейміз, мұнда
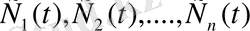 әзірге белгісіз функциялар. Олар үшін теңдеулер жүйесі
әзірге белгісіз функциялар. Олар үшін теңдеулер жүйесі
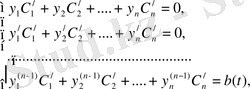
алынады. Жүйені
 бойынша шешеміз
бойынша шешеміз
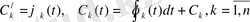 .
.

Бей біртекті (1. 7) теңдеудің жалпы шешімі.
2 ДИФФЕРЕНЦИАЛДЫҚ ТЕҢДЕУЛЕРДІ ШЕШУДЕ
ОПЕРАЦИЯЛЫҚ ЕСЕПТЕУЛЕРДІ ҚОЛДАНУ
2. 1 Лаплас түрлендіруі және оның қасиеттері
Операциялық есептеулердің незгізі Лаплас түрлендіруі болып табылады.
Берілген
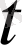 айнымалылы
айнымалылы
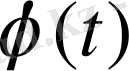 функциясы және
функциясы және
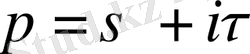 комплекс саны берілсін.
комплекс саны берілсін.
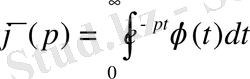 (2. 1)
(2. 1)
теңдігімен анықталған
 функциясы Лаплас түрлендіруі деп аталады.
функциясы Лаплас түрлендіруі деп аталады.
Түрлендіру функциясы анықталу үшін (2. 1) интегралдың қандай да бір облыстың
 мәнінде бар болуы жеткілікті. Ал олыстың сыртында бұл интегралдың мағынасы болмауы мүмкін.
мәнінде бар болуы жеткілікті. Ал олыстың сыртында бұл интегралдың мағынасы болмауы мүмкін.
Мысалы,
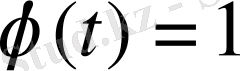 болса, онда
болса, онда
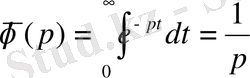 . Бұл интегралды есептегенде
. Бұл интегралды есептегенде
 -ның нақты мәні оң деп қарастырамыз, яғни
-ның нақты мәні оң деп қарастырамыз, яғни
 . Ал
. Ал
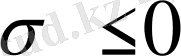 болса, интегралдың мағынасы жоқ, бірақ
болса, интегралдың мағынасы жоқ, бірақ
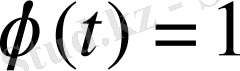 функциясының түрлендіруі барлық жерде
функциясының түрлендіруі барлық жерде
 .
.
Екінші мысал ретінде
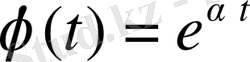 функциясын қарастырайық, мұндағы
функциясын қарастырайық, мұндағы
 - нақты сан.
- нақты сан.
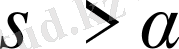 болғанда,
болғанда,
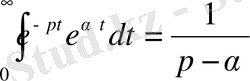 , бұдан
, бұдан
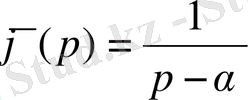 болады. Соңғы интеграл
болады. Соңғы интеграл
 болғанда, интеграл мағынасын жоғалтады, бірақ
болғанда, интеграл мағынасын жоғалтады, бірақ
 -ның кез келген мәнінде
-ның кез келген мәнінде
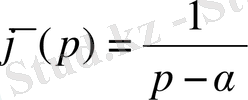 деп қарастырамыз.
деп қарастырамыз.
Кейбір жағдайда,
 -ның кез келген мәнінде (1) интегралдың мәні болмайды. Бұл жағдайда түрлендіру болмайды. Бірақ, физикалық мағынада мұндай функциялардың Лаплас түрлендіруі орындалуы мүмкін. Егер
-ның кез келген мәнінде (1) интегралдың мәні болмайды. Бұл жағдайда түрлендіру болмайды. Бірақ, физикалық мағынада мұндай функциялардың Лаплас түрлендіруі орындалуы мүмкін. Егер
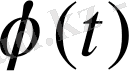 функциясы
функциясы
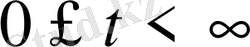 интервалында шектелген немесе
интервалында шектелген немесе
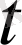 бойынша өседі,
бойынша өседі,
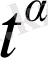 немесе
немесе
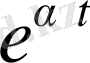 , мұндағы
, мұндағы
 - оң сан болса, онда түрлендіру функция бар болады.
- оң сан болса, онда түрлендіру функция бар болады.
Біз қарастыратын мәселелерде, бұл шарттар міндетті түрде орындалады, яғни барлық жағдайларда түрлендіру функцияның бар болуы туралы сұрақ оң мағынада шешіледі.
Нақты айнымалы
t
-ның
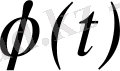 функциясы үшін мына шарттар орындалсын:
функциясы үшін мына шарттар орындалсын:
1) Айнымалы
t
-ның
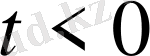 мәндерінде функция мәні
мәндерінде функция мәні
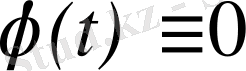 болсын;
болсын;
2) Нақты айнымалы
t
-ның
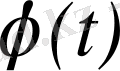 функциясы барлық
функциясы барлық
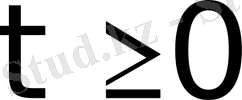 мәндерінде үздіксіз болсын.
мәндерінде үздіксіз болсын.
Үздіксіздік шарты тек бірінші текті үзіліс нүктелерінде ғана орындалмасын және ондай нүктелер саны шектеулі болсын;
3) Берілген
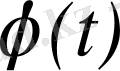 функциясының
функциясының
 өсу дәрежесі шектеулі болсын, яғни барлық
өсу дәрежесі шектеулі болсын, яғни барлық
 мәндерінде
мәндерінде
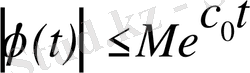 теңсіздігі орындалатындай
теңсіздігі орындалатындай
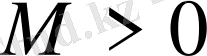 және
және
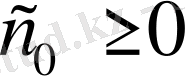 сандары табылсын. Осы шартты қанағаттандыратын
сандары табылсын. Осы шартты қанағаттандыратын
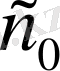 сандарының ең кішісі
сандарының ең кішісі
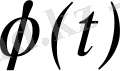 функциясының өсу көрсеткіші деп аталады.
функциясының өсу көрсеткіші деп аталады.
Осы (1) -(3) шарттарды қанағаттандыратын
 функциясы түпнұсқа деп аталады.
функциясы түпнұсқа деп аталады.

теңдігімен анықталған
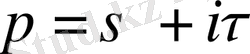 комплекс айнымалының
комплекс айнымалының
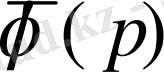 функциясы
функциясы
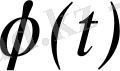 функциясының Лаплас бойынша бейнесі деп аталады. Осы теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
функциясының Лаплас бойынша бейнесі деп аталады. Осы теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:

Мұндағы
 оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
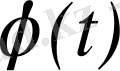 функциясы мен оның
функциясы мен оның
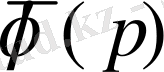 бейнесі арасында сәйкестік орнатылады.
бейнесі арасында сәйкестік орнатылады.
Берілген
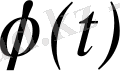 функциясы бойынша оның
функциясы бойынша оның
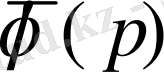 бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:

Егер
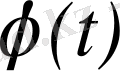 функцияға
функцияға
 бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
 немесе
немесе
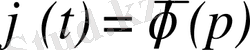 .
.
Автоматты жүйелердегі құбылыстарды сипаттағанда кездесетін көптеген функциялар түпнұсқа болады. Мысалы, Хевисайдтың бірлік функциясы деп аталатын
 функциясы,
функциясы,

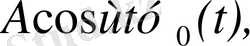
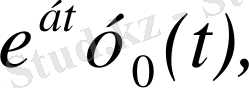

 функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
Осы уақытты алғашқы
 уақыт кезеңі ретінде алуға болады. Сонда t
уақыт кезеңі ретінде алуға болады. Сонда t
 болғанда
ϕ(t) =0
болады да түпнұсқаның (1) шарты орындалады. Ал (2) және (3) шарттар автоматты жүйелерді сипаттайтын көптеген
ϕ(t)
функциялары үшін орындалады.
болғанда
ϕ(t) =0
болады да түпнұсқаның (1) шарты орындалады. Ал (2) және (3) шарттар автоматты жүйелерді сипаттайтын көптеген
ϕ(t)
функциялары үшін орындалады.
Егер осы (1) -(3) шарттардың ең болмағанда біреуі орындалмаса, онда
ϕ
(t) функциясы түпнұсқа болмайды. Мысалы,

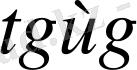 функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
Түпнұсқаның (3) шартын қанағаттандыратын функциялардың мысалын келтірейік:
а) Барлық шектелген функциялар; мұндай функциялар үшін өсу көрсеткіші
 өйткені
өйткені
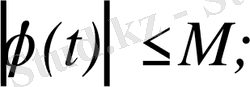
б) Барлық
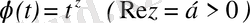 түріндегі дәрежелік функциялар. Бұлар үшін
түріндегі дәрежелік функциялар. Бұлар үшін
 болады. Шынында да
болады. Шынында да

өйткені
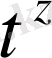 -тің модулі
-тің модулі
 көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы
көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы
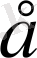 -қаншалықты болса да аз оң сан.
-қаншалықты болса да аз оң сан.
Осыдан
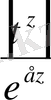 функциясының
функциясының
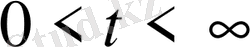 аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
 мәндері үшін
мәндері үшін
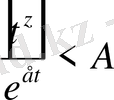 , немесе
, немесе
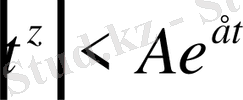 теңсіздігі орындалады.
теңсіздігі орындалады.
Мұндағы
А-
кез-келген оң сан,
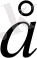 -қаншалықты болса да аз оң сан. Сондықтан
-қаншалықты болса да аз оң сан. Сондықтан
 функциясының өсу көрсеткіші
функциясының өсу көрсеткіші
 болады.
болады.
Егер
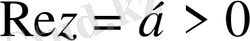 болса, онда
болса, онда
 үзіліс нүктесі болады да
үзіліс нүктесі болады да
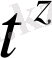 функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
Түрлендіру функциясының кейбір қасиеттері.
Түрлендіру функциясының туындысын қарастырайық.
Айталық,
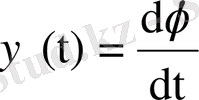 болсын, онда анықтама бойынша
болсын, онда анықтама бойынша
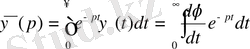 ;
;
бөліктеп интегралдау әдісін қолданамыз:
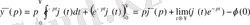 .
.
Ал
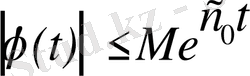 болғандықтан,
болғандықтан,
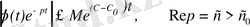 бағалауын аламыз.
бағалауын аламыз.
Сондықтан
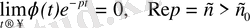 болады да,
болады да,
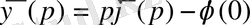 (2. 2)
(2. 2)
сәйкестігін аламыз.
Бұл қасиетті жалпылауға болады. (2. 2) формуланы тізбектеп пайдаланамыз. Егер
 болса, онда
болса, онда
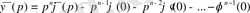 .
.
Енді
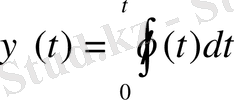 функциясын қарастырайық. Онда
функциясын қарастырайық. Онда
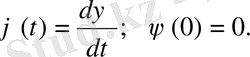
(2. 2) формуланы пайдалансақ, онда
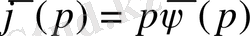 немесе
немесе
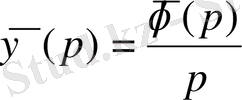 . (2. 3)
. (2. 3)
Операциялық есептеулер арқылы сызықты дифференциалдық теңдеулерді интегралдау әдісін алдымен ізделінді функцияны табу емес, оған сәйкес Лаплас түрлендіру бойынша дифференциалдық теңдеуді қанағаттандыратын функцияны табуға келтіріледі.
Мысалы.
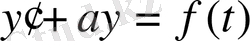 ,
,
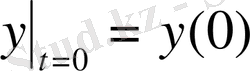
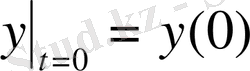 берілген дифференциалдық теңдеудің түрлендіру функциясын құрыңыз. Мұндағы
берілген дифференциалдық теңдеудің түрлендіру функциясын құрыңыз. Мұндағы
 - тұрақты сан.
- тұрақты сан.
Берілген теңдеудің екі жағын
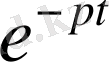 функцияға көбейтеміз және
функцияға көбейтеміз және
 -ден
-ден
 -ке дейін интегралдаймыз:
-ке дейін интегралдаймыз:
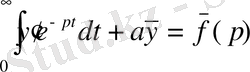
аламыз және (2. 2) формуласын қолданамыз. Сонымен,
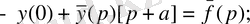
Осыдан,
 , мұндағы
, мұндағы
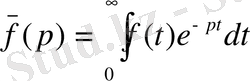 .
.
Осылайша, екінші ретті коэффициенттері тұрақты дифференциалдық теңдеудің шешімін табуға болады.
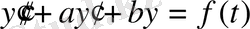 теңдеуінің екі жағында
теңдеуінің екі жағында
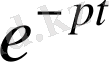 функцияға көбейтеміз және
функцияға көбейтеміз және
 -ден
-ден
 -ке дейін интегралдаймыз:
-ке дейін интегралдаймыз:
 ,
,
Мұндағы
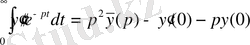 ,
,
 ,
,
сонымен қатар,
 .
.
Демек,
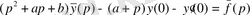 . Осыдан,
. Осыдан,
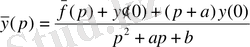 .
.
Бұл мысалдар кез келген ретті дифференциалдық теңдеулердің түрлендіру функциясын құруға болатындығын көрсетеді.
- Лаплас түрлендіруі арқылы ізделінді функцияны анықтау
Дифференциалдық теңдеулердің шешімін Лаплас түрлендіруі арқылы шешу немесе түпнұсқаны бейнесі бойынша анықтау мәселесін қарастырамыз. Бұл мәселе
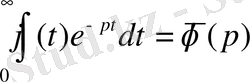
түрдегі интегралдық теңдеуді шешуге әкеледі. Мұндағы
 -
-
 -ға тәуелді белгілі функция, ал ізделінді функция интеграл астындағы
-ға тәуелді белгілі функция, ал ізделінді функция интеграл астындағы
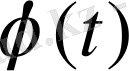 функциясы болады.
функциясы болады.
Бұл интегралдық теңдеу Лаплас теңдеуі деп аталды және онық шешімі жалпы түрде табылады. Бірақ біз бұл теңдеудің жалпы шешімін емес, оның арнайы бір жағдайын қарастырумен шектелеміз. Жалпы шешімі Риман - Меллин формуласымен анықталады. Ал арнайы бір дербес шешімін табу элементар теориямен шектелгенмен, көптеген қызықты есептер шығаруға көмектеседі.
Лапластың интегралдық теңдеуінің кейбір қасиеттері:
1. Оң жағы
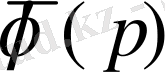 болатын Лаплас теңдеуінің шешімі
болатын Лаплас теңдеуінің шешімі
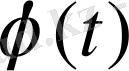 функциясы болсын, яғни
функциясы болсын, яғни
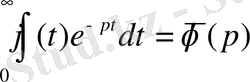 орындалады және
орындалады және
 - қандай да бір сан болсын, онда
- қандай да бір сан болсын, онда
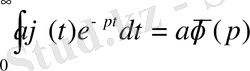 болады.
болады.
Демек, теңдеудің оң жағы тұрақты санға көбейтілсе, онда Лаплас теңдеуінің шешіміде сол санға көбейтіледі.
2. Лаплас теңдеуінің оң жағы
 -ға тәуелді белгілі функциялар қосындысынан тұрсын, яғни
-ға тәуелді белгілі функциялар қосындысынан тұрсын, яғни
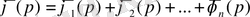 болсын.
болсын.
Теңдеулердің шешімін табайық:
 ;
;
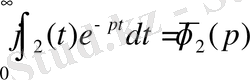 ;
;
. . .
 .
.
Осы теңдіктерді қосатын болсақ, онда

болады.
Осыдан,
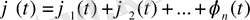 функциясы
функциясы
 теңдеудің шешім деген қортындыға келеміз.
теңдеудің шешім деген қортындыға келеміз.
Бұл қасиеттер қарастырылып отырған Лаплас теңдеуінің қандай да бір дербес шешімін табуға көмектеседі.
Енді Лаплас теңдеуінің оң жағы рационалды бөлшек болған жағдайдағы шешімді іздейміз.
Қарастырылып отырған теңдеу
 (2. 4)
(2. 4)
түрде болсын. Мұндағы
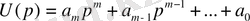 және
және
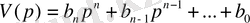 - көпмүшеліктер, сонымен бірге
- көпмүшеліктер, сонымен бірге
 .
.
Айталық,
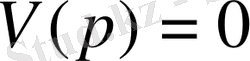 (2. 5)
(2. 5)
болғанда тек ғана нақты түбірлері болсын, яғни
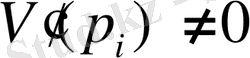 , мұндағы
, мұндағы
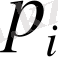 - (2. 5) теңдеудің түбірлері.
- (2. 5) теңдеудің түбірлері.
Бұл жағдайда
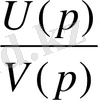 рационалды бөлшек қарапайым бөлшектерге жіктеледі, яғни
рационалды бөлшек қарапайым бөлшектерге жіктеледі, яғни
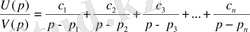
немесе
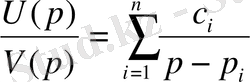 ,
,
мұндағы
 - тұрақты коэффициенттер.
- тұрақты коэффициенттер.
Бұл коэффициенттерді анықтау үшін (2. 6) теңдіктің екі жағында
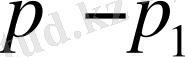 көбейтеміз. Ендеше,
көбейтеміз. Ендеше,
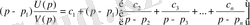 .
.
 болсын делік, онда теңдіктіктің оң жағындағы екінші қосылғыштың көбейткіші
болсын делік, онда теңдіктіктің оң жағындағы екінші қосылғыштың көбейткіші
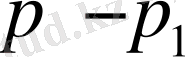 -тен тұрғандықтан нольге айналады. Ал теңдіктің сол жағы анықталмағандық, себебі
-тен тұрғандықтан нольге айналады. Ал теңдіктің сол жағы анықталмағандық, себебі
 болғанда,
болғанда,
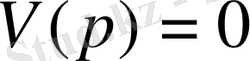 болады. Бұл анықталмағандықты Лопиталь формуласын пайдаланып табамыз, яғни
болады. Бұл анықталмағандықты Лопиталь формуласын пайдаланып табамыз, яғни
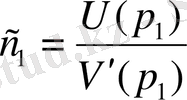 ,
,
мұндағы
 -
-
 мәніндегі функцияның
мәніндегі функцияның
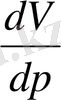 бойынша алынған туындысы.
бойынша алынған туындысы.
Дәл осылайша,
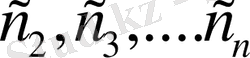 мәндерін анықтаймыз. Демек,
мәндерін анықтаймыз. Демек,
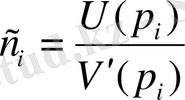 ,
,
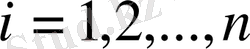 .
.
Қарапайым бөлшектерге жіктелген рационал бөлшек:
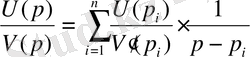 .
.
Алмастыру арқылы
 функциясы
функциясы
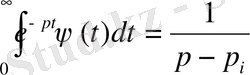
интегралдық теңдеуді қанағаттандыратынын аламыз.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz