Сандық және функционалдық қатарлар: жинақтылық критерийлері, дәрежелік және Тейлор қатарлары, екі еселі интегралдар


ҚАТАРЛАР
Бұл курста біз сандық және функционалдық қатарларды қарастырамыз.
Сандық қатарлар
Анықтама 1.
Берілген шектеусіз сандар тізбегі
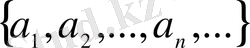 үшін:
үшін:
 (1)
(1)
өрнегі сандық қатар деп аталады, мұндағы
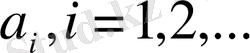 сандары - қатардың мүшелері.
сандары - қатардың мүшелері.
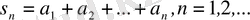 саны қатардың бөлік қосындысы деп аталады.
саны қатардың бөлік қосындысы деп аталады.
Анықтама 2
.
Егер
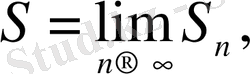 шегі табылатын болса, онда
шегі табылатын болса, онда
 (1) қатарының қосындысы деп аталады.
(1) қатарының қосындысы деп аталады.
Анықтама 3.
Қатар жинақты деп аталады, егер
 тұрақты санға тең болса, кері жағдайда, яғни,
тұрақты санға тең болса, кері жағдайда, яғни,
 шегі шексіздікке тең болса немесе табылмаса, онда қатар жинақсыз деп аталады.
шегі шексіздікке тең болса немесе табылмаса, онда қатар жинақсыз деп аталады.
Мысал 1.
Қатардың қосындысын тап
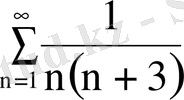 .
.
Шешуі. Қатардың жалпы мүшесі:
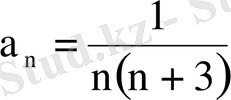 =
=
 .
.
Алынған формуланы қолданып, қатардың
 -ші бөлік қосындысын табайық :
-ші бөлік қосындысын табайық :
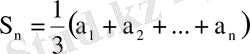
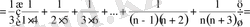
=

=
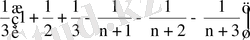 .
.
Сонымен,
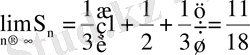 .
.
Ендеше, берілген қатар жинақты және оның қосындысы
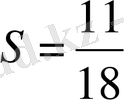 .
.
Мысал 2.
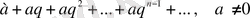 түріндегі қатарды (геометриялық прогрессия) қарастырайық. Онда бөлік қосынды:
түріндегі қатарды (геометриялық прогрессия) қарастырайық. Онда бөлік қосынды:
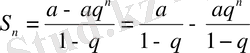
- Егер
- Егер- табылмайды.
- Егер, онда
а)
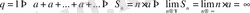 (
(
 болса)
болса)
б)
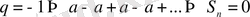 , егер
, егер
 -жұп болса және
-жұп болса және
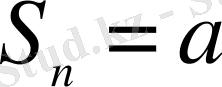 , егер
, егер
 -тақ болса,
-тақ болса,
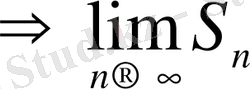 - табылмайды.
- табылмайды.
Сонымен, қатар
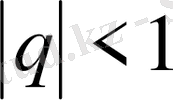 болғанда ғана жинақты.
болғанда ғана жинақты.
Қатардың соңғы мүшелерін лақтырып тастағаннан оның жинақтылығы өзгермейді. Жинақты қатар:
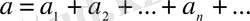
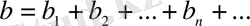 .
.
үшін келесі теңдіктер орынды:
а)
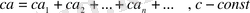
б)
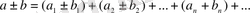
Теорема 1. Қатардың жинақтылығының қажетті шарты.
(1) қатары жинақты болуы үшін
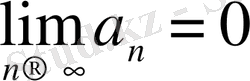 болуы қажетті.
болуы қажетті.
Мысал 3.
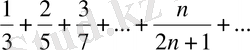 қатары жинақсыз, себебі қатардың жинақтылығының қажетті шарты орындалмайды:
қатары жинақсыз, себебі қатардың жинақтылығының қажетті шарты орындалмайды:
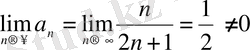 .
.
 болу шартынан қатардың жинақты екені шықпайды.
болу шартынан қатардың жинақты екені шықпайды.
Таңбасы оң қатарлар
2-мысалда көрсетілгендей
 бөлік қосындысының ақырлы формуласын анықтау кей жағдайларда қиындық туғызуы мүмкін. Сондықтан, қатардың жалпы мүшесін білу ғана жеткілікті болатын қатардың жинақтылығының жеткілікті белгілерін білген жөн. Тек қана таңбалары оң қатарлар үшін ғана ақиқат болатын белгілерге тоқталайық.
бөлік қосындысының ақырлы формуласын анықтау кей жағдайларда қиындық туғызуы мүмкін. Сондықтан, қатардың жалпы мүшесін білу ғана жеткілікті болатын қатардың жинақтылығының жеткілікті белгілерін білген жөн. Тек қана таңбалары оң қатарлар үшін ғана ақиқат болатын белгілерге тоқталайық.
Мүшелері оң сандар болатын қатарларды қарастырамыз:
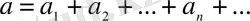 (2)
(2)
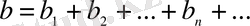 (3)
(3)
Теорема 2. Салыстыру белгілері :
1. Егер қандай да бір
 нөмірінен бастап,
нөмірінен бастап,
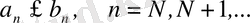 теңсіздігі орынды болса, онда
теңсіздігі орынды болса, онда
а) (3) қатарының жинақтылығынан (2) қатарының жинақты екені шығады,
б) (2) қатарының жинақсыздығынан (3) қатарының жинақсыз екені шығады.
2. Егер
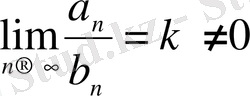 ақырлы шегі табылса, онда (1) және (2) қатарлары не екеуі де бірдей жинақты, не екеуі де бірдей жинақсыз.
ақырлы шегі табылса, онда (1) және (2) қатарлары не екеуі де бірдей жинақты, не екеуі де бірдей жинақсыз.
Мысал 4. Қатарды жинақтылыққа зертте:
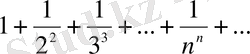 (4)
(4)
Жинақты (мысал 1,
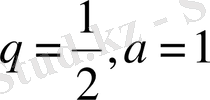 ) болатын
) болатын
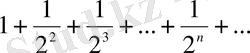
қатарын қарастыралық,
 үшін:
үшін:
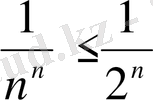 болғандықтан,
болғандықтан,
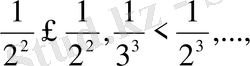 ендеше (4) қатары жинақты.
ендеше (4) қатары жинақты.
Теорема 3-4. Даламбер белгісі (Коши)
. Егер
 , мұндағы
, мұндағы
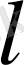 -ақырлы сан болса, онда:
-ақырлы сан болса, онда:
а) егер
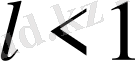 болса, онда (1) қатары жинақты,
болса, онда (1) қатары жинақты,
б) егер
 болса, (1) қатары жинақсыз,
болса, (1) қатары жинақсыз,
в)
 қатардың жинақтылығы туралы сұрақ ашық қалады.
қатардың жинақтылығы туралы сұрақ ашық қалады.
Мысал 5. Қатарды жинақтылыққа зертте:
а)
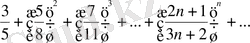
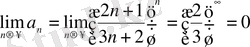 , яғни, жинақтылықтың қажетті шарты орындалады. Коши белгісін қолданамыз:
, яғни, жинақтылықтың қажетті шарты орындалады. Коши белгісін қолданамыз:
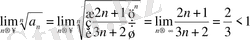 - қатар жинақты.
- қатар жинақты.
б) гармониялық қатар үшін:
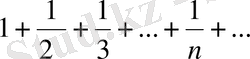
Жинақтылықтың қажетті шарты :
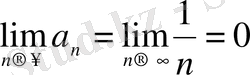 орындалады. Даламбер белгісін қолданамыз:
орындалады. Даламбер белгісін қолданамыз:
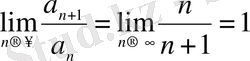 -жинақтылық туралы сұрақ ашық қалады.
-жинақтылық туралы сұрақ ашық қалады.
Мысал 6.
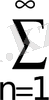
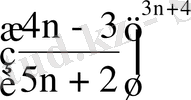 .
.
Шешуі.
 =
=
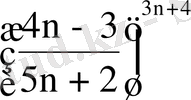 болады. Коши белгісін қолдансақ:
болады. Коши белгісін қолдансақ:
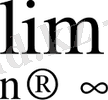
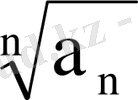 =
=
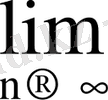
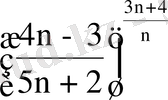 =
=
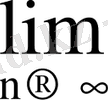
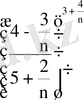 =
=
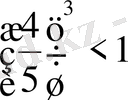 .
.
Яғни, берілген қатар жинақты.
Теорема 5. Кошидің интегралдық белгісі
. Қандай да бір
 нөмірінен бастап
нөмірінен бастап
 теңсіздігі орындалсын және
теңсіздігі орындалсын және
 функциясы мынадай үзіліссіз өспелі емес функция болсын:
функциясы мынадай үзіліссіз өспелі емес функция болсын:
 . Онда, егер
. Онда, егер
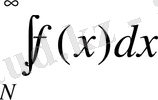 жинақты (жинақсыз) болса, онда (1) қатары жинақты (жинақсыз) .
жинақты (жинақсыз) болса, онда (1) қатары жинақты (жинақсыз) .
Мысал 7. Берілген қатарды жинақтылыққа зертте:
 ,
,
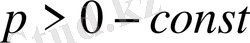 . (5)
. (5)
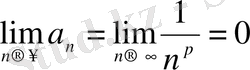 - қатардың жинақтылығының қажетті шарты орындалады.
- қатардың жинақтылығының қажетті шарты орындалады.
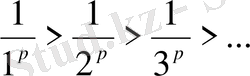 болғандықтан,
болғандықтан,
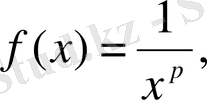
 деп алып, Кошидің интегралдық белгісін қолдансақ;
деп алып, Кошидің интегралдық белгісін қолдансақ;
а)
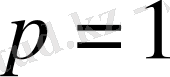 болса, онда
болса, онда
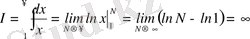 , яғни, интеграл жинақсыз. б)
, яғни, интеграл жинақсыз. б)
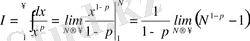 .
.
Бұл интеграл
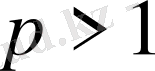 болғанда жинақты, ал
болғанда жинақты, ал
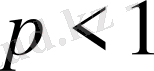 жинақсыз.
жинақсыз.
Ендеше, (5) қатары
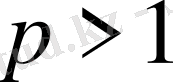 болғанда ғана жинақты, ал қалған жағдайларда жинақсыз.
болғанда ғана жинақты, ал қалған жағдайларда жинақсыз.
Егер р=1 болса, (5) қатары біз жоғарыда 5-мысалда қарастырған гармониялық қатар болады және ол жинақсыз. Ал
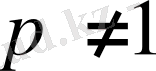 болса, онда (5) Дирихле қатары деп аталады.
болса, онда (5) Дирихле қатары деп аталады.
Мысал 8.
Қатарды жинақтылыққа зертте:
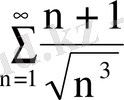 .
.
Шешуі.
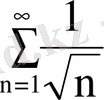 қатарымен салыстыралық, бұл қатар көрсеткіші
қатарымен салыстыралық, бұл қатар көрсеткіші
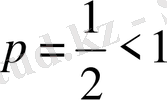 болатын Дирихле қатары және ол жинақсыз.
болатын Дирихле қатары және ол жинақсыз.
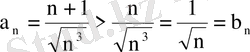 . Ендеше, салыстырудың бірінші белгісі бойынша берілген қатар жинақсыз.
. Ендеше, салыстырудың бірінші белгісі бойынша берілген қатар жинақсыз.
20. 3 Таңбалары ауыспалы қатарлар
 , (6)
, (6)
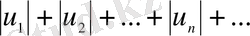 , (7)
, (7)
қатарларын қарастырамыз.
Анықтама 4.
(6) сандық қатарының мүшелері деп аталатын
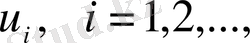 … оң да, теріс те болатын болса, онда бұл қатар таңбалары ауыспалы қатар деп аталады.
… оң да, теріс те болатын болса, онда бұл қатар таңбалары ауыспалы қатар деп аталады.
Таңбалары алма-кезек ауыспалы қатар (6) қатарының дербес жағдайы:
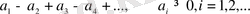 (8)
(8)
Лейбниц белгісі
. Егер (8) қатарының мүшелері үшін қандай да бір
 нөмірінен бастап
нөмірінен бастап
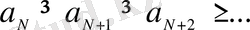 теңсіздігі орындалып және
теңсіздігі орындалып және
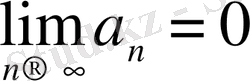 болса, онда (8) қатары жинақты және оның қосындысы оң сан.
болса, онда (8) қатары жинақты және оның қосындысы оң сан.
Теорема 6. Егер (7) қатары жинақты болса, онда (6) қатары да жинақты.
Егер (6) қатары жинақты болып, ал (7) қатары жинақсыз болса, онда (6) қатары шартты жинақты деп аталады. Егер (7) қатары жинақты болып және сонымен қатар, (6) қатары да жинақты болса, онда (6) қатары абсолютті жинақты деп аталады. (6) таңбалары ауыспалы қатардың жинақтылығы туралы сұрақ, жалпы жағдайда, таңбалары оң қатар (7) -нің жинақтылығымен шешіледі. Ал таңбалары оң қатардың жинақтылық белгілерін жоғарыда қарастырдық.
Мысал 9.
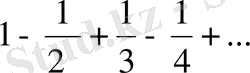 (9)
(9)
қатары Лейбниц белгісі бойынша жинақты, ал оның абсолют шамаларынан құрылған қатар (гармониялық қатар) жинақсыз. Ендеше, (9) қатары шартты жинақты.
Мысал 10.
 .
.
Шешуі.
Берілген қатардың абсолют шамаларынан құралған қатарды қарастырамыз:
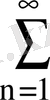
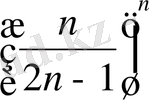 .
.
Бұл қатар Коши белгісі бойынша жинақты:
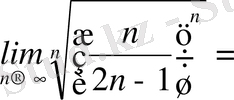
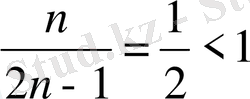 .
.
Сонымен, берілген қатар абсолютті жинақты.
Мысал 11.
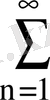
 .
.
Шешуі.
Берілген қатардың абсолют шамаларынан құралған қатарды қарастырамыз:
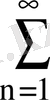
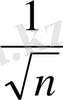 , бұл қатар көрсеткіші
, бұл қатар көрсеткіші
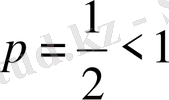 болатын Дирихле қатары.
болатын Дирихле қатары.
Берілген қатар таңбасы алма-кезек ауыспалы қатар болғандықтан, Лейбниц белгісін қолдансақ:
- >, яғни, қатардың мүшелерінің тізбегі кемімелі;
- ==0.
Ендеше, берілген қатар шартты жинақты.
- Өз бетімен шығаруға арналған есептер
Келесі есептерді өз беттеріңмен шығарыңдар:
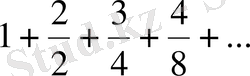
- Қатардың қосындысын тап:.
- Қатардың- ші мүшесінің формуласын жаз:
а)
 ; б)
; б)
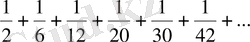 .
.
- Белгіліжалпы мүшесі бойынша қатардың алғашқы төрт мүшесін жаз.
а)
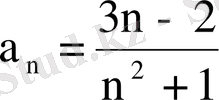 ; б)
; б)
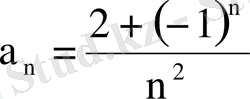 ; в)
; в)
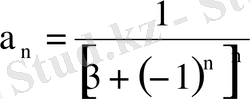 .
.
Таңбасы оң қатарларды жинақтылыққа зертте:
4.
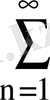
 ; 5.
; 5.
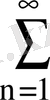
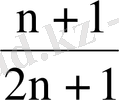 ; 6.
; 6.
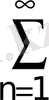
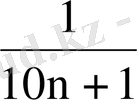 ;
;
7.
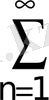
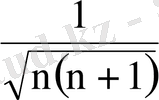 ; 8.
; 8.
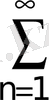
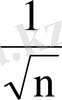 ; 9.
; 9.
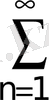
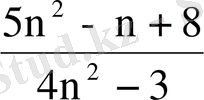 ;
;
10.
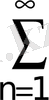
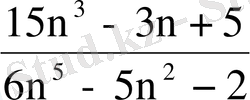 ; 11.
; 11.
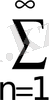
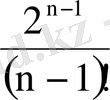 ; 12.
; 12.
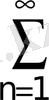
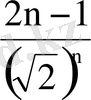 ;
;
13.
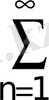
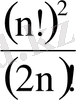 ; 14.
; 14.
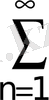
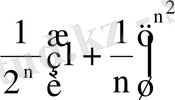 ; 15.
; 15.
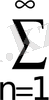
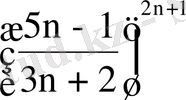 ;
;
16.
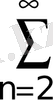
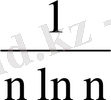 ; 17.
; 17.
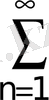
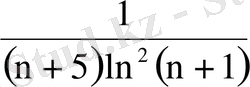 ;
;
18.
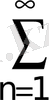
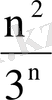 ; 19.
; 19.
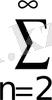
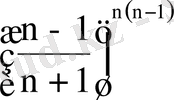 ; 20.
; 20.
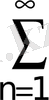
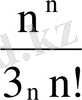 .
.
21. Келесі қатарларды абсолютті және шартты жинақтылыққа зертте.
1.
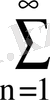
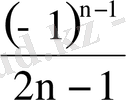 ; 2.
; 2.
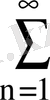
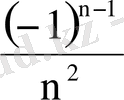 ; 3.
; 3.
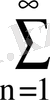
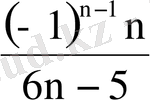 ;
;
4.
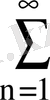
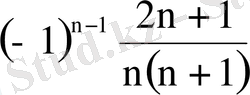 ; 5.
; 5.
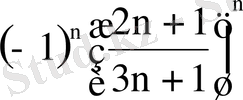 ;
;
6.
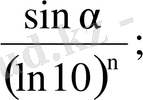
21. 5 Сұрақтар
1. Сандық қатардың анықтамасы.
2. Қатардың бөлік қосындысы.
3. Қатардың қосындысының анықтамасы.
4. Сандық қатардың жинақтылығы мен жинақсыздығы.
5. Жинақтылықтың қажетті шарты.
6. Таңбалары оң қатарды салыстырудың бірінші белгісі.
7. Таңбалары оң қатарды салыстырудың екінші белгісі.
8. Даламбер белгісі.
9. Коши белгілері.
10. Таңбалары ауыспалы қатарлар. Абсолютті және шартты жинақтылық.
11. Таңбалары алма-кезек ауыспалы қатарлар. Лейбниц белгісі.
21 ФУНКЦИОНАЛДЫҚ ҚАТАРЛАР
21. 1 Функционалдық қатарлар
Анықтама 1. Функционалдық қатар деп:
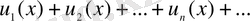 , (1)
, (1)
мұндағы
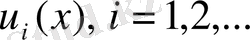 қатардың мүшелері функциялар болатын қатарды айтамыз.
қатардың мүшелері функциялар болатын қатарды айтамыз.
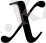 қандай да бір тұрақты мән берсек, (1) қатары сандық қатарға айналады. Сонымен,
қандай да бір тұрақты мән берсек, (1) қатары сандық қатарға айналады. Сонымен,
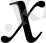 -тің қандай да бір мәндерінде (1) қатары жинақты, қандай да бір мәндерінде жинақсыз.
-тің қандай да бір мәндерінде (1) қатары жинақты, қандай да бір мәндерінде жинақсыз.
Анықтама 2.
(1) қатары жинақты болатын
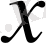 мәндер жиыны функционалдық қатардың жинақтылық облысы деп аталады.
мәндер жиыны функционалдық қатардың жинақтылық облысы деп аталады.
Қатардың жинақтылық облысында қатардың қосындысы
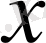 -ке байланысты функция болатындықтан, қатардың қосындысын
-ке байланысты функция болатындықтан, қатардың қосындысын
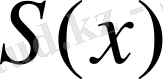 деп белгілейміз.
деп белгілейміз.
Мысал 1
.
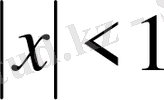 болған жағдайда,
болған жағдайда,
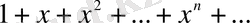 қатары жинақты. Себебі, бұл қатар кемімелі геометриялық прогрессия (
қатары жинақты. Себебі, бұл қатар кемімелі геометриялық прогрессия (
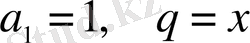 ) және оның қосындысы
) және оның қосындысы
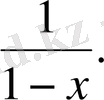 Сонымен, (-1, 1) интервалында берілген қатар жинақты және
Сонымен, (-1, 1) интервалында берілген қатар жинақты және
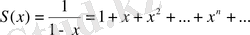 .
.
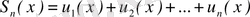 болса, онда
болса, онда
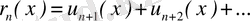 - қатардың қалдық мүшесі.
- қатардың қалдық мүшесі.
Теорема 1 . (1) қатарының жинақтылық облысында:
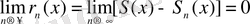 .
.
21. 1. 1 Бірқалыпты жинақтылық. Функционалдық қатарларға қолданылатын амалдар
Анықтама 3.
(1) қатары
 облысында мажорланған деп аталады, егер
облысында мажорланған деп аталады, егер
 үшін :
үшін :
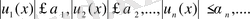
теңсіздігі орындалатындай,
 , (2)
, (2)
таңбалары оң жинақты сандық қатар табылса.
Мысал 2.
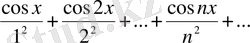
қатары барлық сан осінде мажорланған екені анық, өйткені,
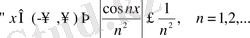 , ал
, ал
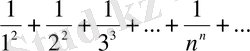 - қатары жинақты қатар (
мысал 5
) .
- қатары жинақты қатар (
мысал 5
) .
 облысында мажорланған қатар, осы
облысында мажорланған қатар, осы
 облысында абсолютті жинақты. .
облысында абсолютті жинақты. .
Анықтама 4.
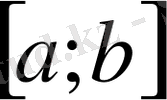 аралығында жинақты (1) қатары бірқалыпты жинақты деп аталады, егер барлық
аралығында жинақты (1) қатары бірқалыпты жинақты деп аталады, егер барлық
 үшін
үшін

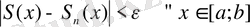 болса.
болса.
Теорема 2.
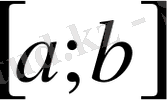 аралығында мажорланған (1) қатары осы кесіндіде бірқалыпты жинақты.
аралығында мажорланған (1) қатары осы кесіндіде бірқалыпты жинақты.
2-теоремадан мажорланған қатар болу бірқалыпты жинақтылықтан да күшті шарт екенін көреміз, яғни, бірқалыпты жинақталатын, бірақ мажорланған емес қатарлар табылады.
Теорема 3.
(1) қатары
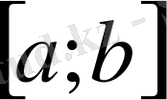 аралығында бірқалыпты жинақты және
аралығында бірқалыпты жинақты және
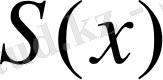 - оның қосындысы болсын. Онда егер:
- оның қосындысы болсын. Онда егер:
1.
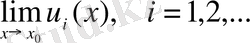 - табылса, онда
- табылса, онда
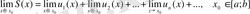
2. қатардың мүшелері
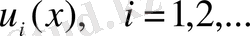 -
-
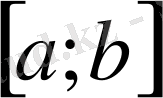 аралығында үзіліссіз және
аралығында үзіліссіз және
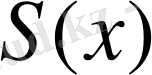 функциясы да
функциясы да
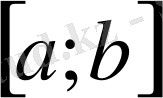 аралығында үзіліссіз болса, онда
аралығында үзіліссіз болса, онда
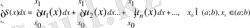 , яғни, қатарды мүшелеп интегралдауға болады.
, яғни, қатарды мүшелеп интегралдауға болады.
Теорема 4.
Егер (1) қатары
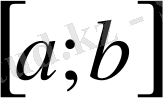 аралығында жинақты болса,
аралығында жинақты болса,
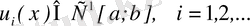 , ал
, ал
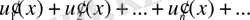 қатары
қатары
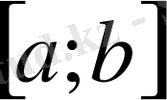 аралығында бірқалыпты жинақты болса, онда
аралығында бірқалыпты жинақты болса, онда
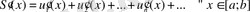 ,
,
яғни, қатарды мүшелеп дифференциалдауға болады.
21. 2 Дәрежелік қатарлар
Дәрежелік қатар функционалдық қатарлардың дербес түрі.
Анықтама 5.
(
 ) -ға қатысты дәрежелік қатар деп:
) -ға қатысты дәрежелік қатар деп:
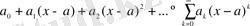 , (3)
, (3)
түрінде берілген қатарды айтамыз, мұндағы
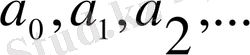 коэффиценттері - тұрақты сандар.
коэффиценттері - тұрақты сандар.
Егер
 болса, онда:
болса, онда:
 (4)
(4)
Теорема 5. (Абель) .
 болғанда (4) қатары жинақты болса, онда ол
болғанда (4) қатары жинақты болса, онда ол
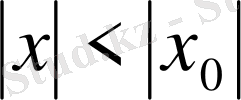 болғанда абсолютті жинақты; ал оның
болғанда абсолютті жинақты; ал оның
 болғанда жинақсыз болуынан,
болғанда жинақсыз болуынан,
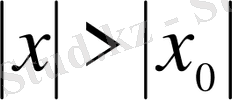 болғанда жинақсыздығы шығады.
болғанда жинақсыздығы шығады.
Абель теоремасынан: (4) қатары үшін жалғыз ғана
 саны,
саны,
 , табылады,
, табылады,
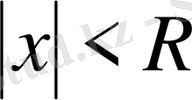 болғанда (2) қатары жинақты, ал
болғанда (2) қатары жинақты, ал
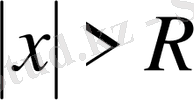 үшін жинақсыз болатындай.
үшін жинақсыз болатындай.
 саны дәрежелік қатардың жинақтылық радиусы деп аталады, ал
саны дәрежелік қатардың жинақтылық радиусы деп аталады, ал
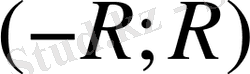 - жинақтылық интервалы деп аталады. Егер
- жинақтылық интервалы деп аталады. Егер
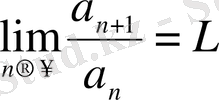 ақырлы шегі табылса, онда
ақырлы шегі табылса, онда
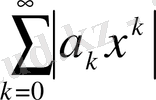 қатарына Даламбер белгісін қолдансақ,
қатарына Даламбер белгісін қолдансақ,
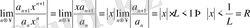 , яғни,
, яғни,
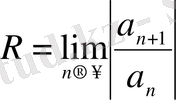 .
.
Дәл осылай, Коши белгісін қолдансақ:
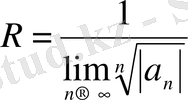 .
.
Мысал 3.
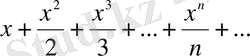 қатарының жинақтылық облысын тап.
қатарының жинақтылық облысын тап.
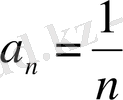 болғандықтан,
болғандықтан,
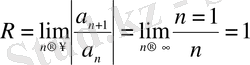 - жинақтылық радиусы.
- жинақтылық радиусы.
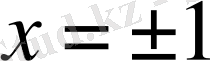 нүктелерінде жинақтылыққа зерттейміз.
нүктелерінде жинақтылыққа зерттейміз.
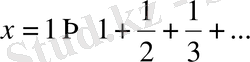 - гармониялық қатар, жинақсыз болады.
- гармониялық қатар, жинақсыз болады.
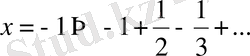 -таңбасы алма-кезек ауыспалы қатар, бұл жинақты қатар (
мысал 6
) . Сонымен, берілген дәрежелік қатардың жинақтылық облысы:
-таңбасы алма-кезек ауыспалы қатар, бұл жинақты қатар (
мысал 6
) . Сонымен, берілген дәрежелік қатардың жинақтылық облысы:
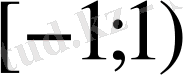 .
.
(3) қатарының жинақтылық интервалы
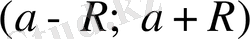 , мұндағы
, мұндағы
 - (4) қатарының жинақтылық радиусы.
- (4) қатарының жинақтылық радиусы.
 -кез келген бүтіндей (3) қатарының жинақтылық интервалының ішінде жататын кесінді болсын. Онда:
-кез келген бүтіндей (3) қатарының жинақтылық интервалының ішінде жататын кесінді болсын. Онда:
- (3) қатары мажорланған ( бірқалыпты жинақты) кесіндісінде.
- (3) қатарының қосындысы жинақтылық интервалында үзіліссіз.
- (3) қатарынкесіндісінде мүшелеп интегралдауға және қанша болса сонша рет мүшелеп дифференциалдауға болады, сонымен қатар, алынған дәрежелік қатардың жинақтылық интервалы (3) қатарының жинақтылық интервалымен бірдей.
Мысал 4.
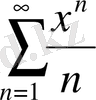 . Дәрежелік қатардың жинақталу аймағын тап.
. Дәрежелік қатардың жинақталу аймағын тап.
Шешуі.
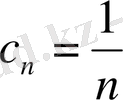 болады, онда жинақтылық радиусы
болады, онда жинақтылық радиусы
 =
=
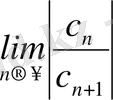 =
=
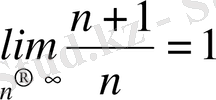 ;
;
(-1, 1) - жинақтылық интервалы.
 болсын, онда берілген қатар:
болсын, онда берілген қатар:
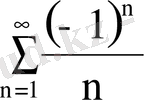 түрінде болады.
түрінде болады.
Бұл қатар шартты жинақты, себебі
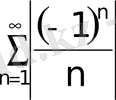 =
=
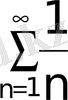 жинақсыз және
жинақсыз және
а)
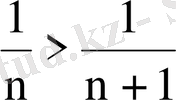 ; б)
; б)
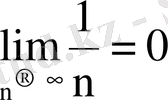 .
.
 болса, берілген қатар
болса, берілген қатар
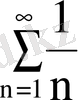 - гармониялық қатар және ол жинақсыз қатар. Сонымен, берілген қатар
- гармониялық қатар және ол жинақсыз қатар. Сонымен, берілген қатар
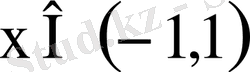 аралығында абсолютті жинақты,
аралығында абсолютті жинақты,
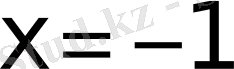 болғанда шартты жинақты.
болғанда шартты жинақты.
Мысал 5.
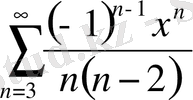 .
.
Шешуі.
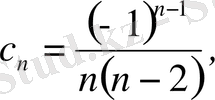
 0 егер
0 егер
 болса.
болса.
Онда
 =
=
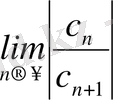 =
=
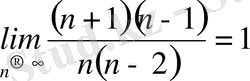 .
.
Сонымен,
 - жинақтылық радиусы;
- жинақтылық радиусы;
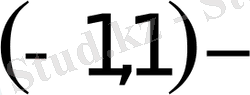 жинақтылық интервалы.
жинақтылық интервалы.
Интервалдың шеткі нүктелерінде берілген қатарды жинақтылыққа зерттейік.
 болса:
болса:
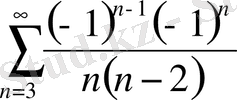 =
=
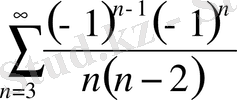 =-
=-
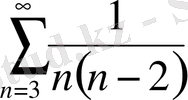
Бұл қатарды
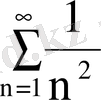 жинақты қатарымен салыстырамыз:
жинақты қатарымен салыстырамыз:
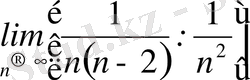 =
=
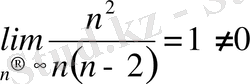 .
.
Сонымен, салыстырудың екінші белгісі бойынша
 болғанда қатар абсолютті жинақты.
болғанда қатар абсолютті жинақты.
Егер
 болса, онда берілген қатар мына түрде болады:
болса, онда берілген қатар мына түрде болады:
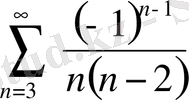 .
.
Бұл қатардың мүшелерінің абсолют шамасынан құрылған қатар:
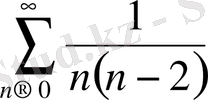 жинақты қатар, ендеше жоғарыдағы таңбасы ауыспалы қатар абсолютті жинақты.
жинақты қатар, ендеше жоғарыдағы таңбасы ауыспалы қатар абсолютті жинақты.
Сонымен, берілген қатар
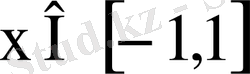 болғанда абсолютті жинақты.
болғанда абсолютті жинақты.
21. 3 Тейлор қатары
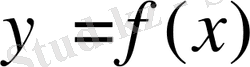 функциясының қандай да бір
функциясының қандай да бір
 нүктесінің аймағында
нүктесінің аймағында
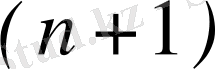 - ші ретті туындысы бар болсын. Дәрежесі
- ші ретті туындысы бар болсын. Дәрежесі
 -нан жоғары емес төмендегі теңдік орындалатын
-нан жоғары емес төмендегі теңдік орындалатын
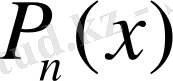 көпмүшелігін табалық:
көпмүшелігін табалық:
(5)
 көпмүшелігін мына түрде іздейміз:
көпмүшелігін мына түрде іздейміз:
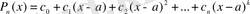
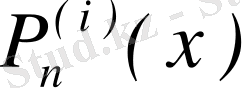 -ті тауып және (5) шартын қолдансақ:
-ті тауып және (5) шартын қолдансақ:
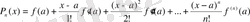 .
.
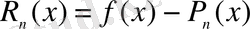 - қалдық мүшесі болсын. Онда
- қалдық мүшесі болсын. Онда
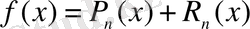 және
және
 -ті Лагранж формасында жазуға болатынын көрсетуге болады:
-ті Лагранж формасында жазуға болатынын көрсетуге болады:
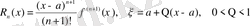
(6)
(6) формуласы Тейлор формуласы деп аталады, ал
 болса, Маклорен формуласы деп аталады.
болса, Маклорен формуласы деп аталады.
Бұл формулалар
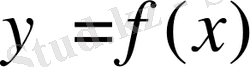 функциясын
функциясын
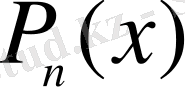 көпмүшелігімен
көпмүшелігімен
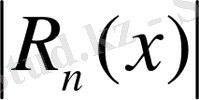 -ға тең дәлдікте айырбастауға мүмкіндік береді.
-ға тең дәлдікте айырбастауға мүмкіндік береді.
Мысал 6.
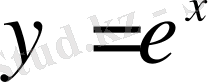 функциясын Маклорен формуласы бойынша жікте және
функциясын Маклорен формуласы бойынша жікте және
 санын
санын
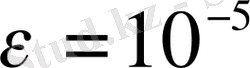 дәлдікке дейін есепте.
дәлдікке дейін есепте.

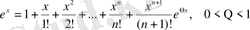
 болса,
болса,
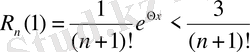 .
.
 үшін:
үшін:
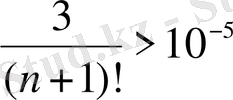 , ал
, ал
 үшін:
үшін:
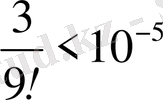 болғандықтан,
болғандықтан,
 . Сонымен,
. Сонымен,
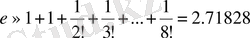 .
.
 нүктесінің аймағында
нүктесінің аймағында
 функциясы шексіз рет дифференциалданатын болсын. Онда
функциясы шексіз рет дифференциалданатын болсын. Онда
 -ді өте үлкен шама деп ала отырып, (4) теңдігінің оң жағында дәрежелік функция аламыз. Қандай шарт орындалғанда бұл қатардың қосындысы
-ді өте үлкен шама деп ала отырып, (4) теңдігінің оң жағында дәрежелік функция аламыз. Қандай шарт орындалғанда бұл қатардың қосындысы
 тең?
тең?
Теорема 6.
Егер
 функциясы
функциясы
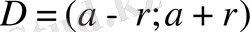 интервалында шектеусіз рет дифференциалданатын болса және
интервалында шектеусіз рет дифференциалданатын болса және
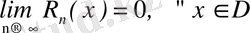 , онда
, онда
 -да:
-да:
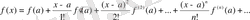 , (7)
, (7)
Әрі, қатардың
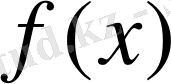 функциясына
функциясына
 -да жинақталуы бірқалыпты.
-да жинақталуы бірқалыпты.
Анықтама 6.
(7) қатары Тейлор қатары деп аталады, ал егер
 болса, ол Маклорен қатары болады.
болса, ол Маклорен қатары болады.
Әрбір элементар функция үшін
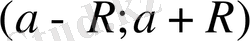 интервалында Тейлор қатарына жіктелетіндей
интервалында Тейлор қатарына жіктелетіндей
 және
және
 сандары табылатындығын айта кеткен жөн.
сандары табылатындығын айта кеткен жөн.
Кейбір функциялардың Тейлор қатарына жіктелуін дәлелдеусіз көрсетеміз:
1.
 ,
,
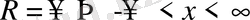
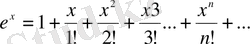
2.
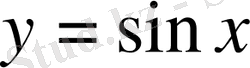 ,
,
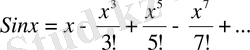
3.
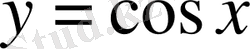 ,
,
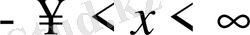
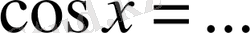
4.
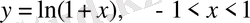
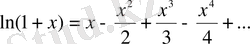
5.
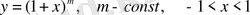
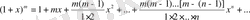
Е с к е р т у . Көрсетілген жіктеулерді күрделі функциялар үшін де қолдануға болады. Мысалы:
1.
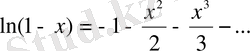 ,
,
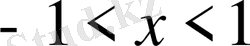
2.
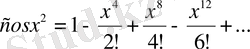 ,
,
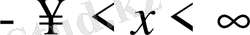
3.
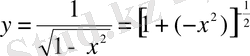 .
.
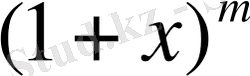 жіктелуіндегі
жіктелуіндегі
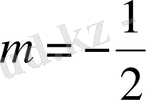 деп есептейміз және х-тің орнына (
деп есептейміз және х-тің орнына (
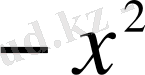 ) -ты қоямыз. жинақтылық интервалы:
) -ты қоямыз. жинақтылық интервалы:
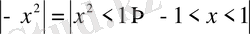 болады және:
болады және:
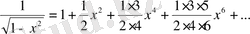 .
.
4)
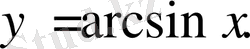
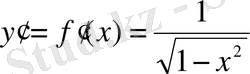 болғандықтан,
болғандықтан,
 үшін:
үшін:
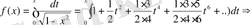
 ,
,
 .
.
Бұл қатар
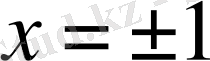 болғанда жинақты екенін көрсетуге болады. Онда
болғанда жинақты екенін көрсетуге болады. Онда
 болғанда:
болғанда:
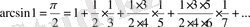 . Бұл
. Бұл
 -ді есептеу формуласы.
-ді есептеу формуласы.
Алғашқы функциясы элементар функциялар болмайтын интегралдарды кейде қатарлардың көмегімен есептеуге болады.
Мысал 7.
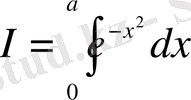 интегралын есепте.
интегралын есепте.
Шешуі.
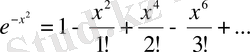 ,
,
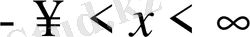 , екенін ескеріп, екі жағын да интегралдасақ:
, екенін ескеріп, екі жағын да интегралдасақ:
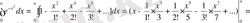
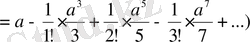 .
.
Тейлор қатары, жалпы айтқанда, дәрежелік қатарлар дифференциалдық теңдеулердің дербес шешімдерін табу үшін жиі қолданылады.
Мысал 8 . Берілген теңдеуінің жалпы шешімін тап:
Шешуі.
 ,
,
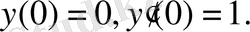
Шешімді
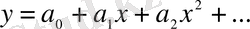 түрінде іздейміз.
түрінде іздейміз.
Бастапқы шарттарды ескерсек:

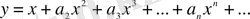
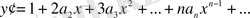
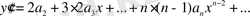
Ары қарай,
 -терді теңдеуге қойып,
-терді теңдеуге қойып,
 -тің бірдей дәрежелерінің коэффиценттерін теңестірсек:
-тің бірдей дәрежелерінің коэффиценттерін теңестірсек:
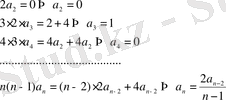
Ендеше,
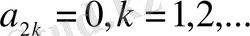 .
.
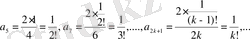
Бұдан, дербес шешім
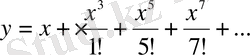
Мысал 9.
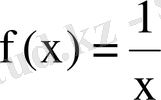 функциясын
функциясын
 аймағындағы Тейлор қатарына жікте.
аймағындағы Тейлор қатарына жікте.
Шешуі. Туындыларын табамыз:
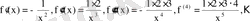
 болғанда:
болғанда:
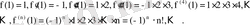
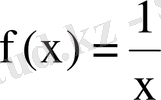 функциясының
функциясының
 аймағындағы Тейлор қатары мына түрде болады:
аймағындағы Тейлор қатары мына түрде болады:
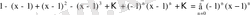 .
.
Алынған қатар еселігі
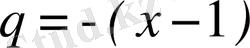 болатын геометриялық қатар:
болатын геометриялық қатар:
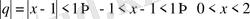 Equation. 3 .
Equation. 3 .
Ендеше, қатар
 аралығында абсолютті жинақты. Онда
аралығында абсолютті жинақты. Онда
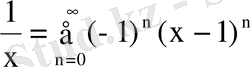 ,
,
 .
.
Мысал 10 . Берілген функцияны Тейлор қатарына жікте:
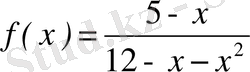 .
.
Шешуі. Берілген бөлшекті қарапайым бөлшектерге жіктейміз:
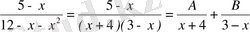 ;
;
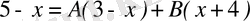 .
.
Бұдан,
 және
және
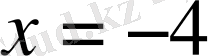 дей отырып,
дей отырып,
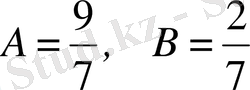 екендігін аламыз. Ендеше,
екендігін аламыз. Ендеше,
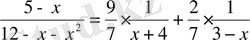 . (8)
. (8)
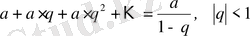 формуласын қолданып, әрбір қарапайым бөлшектерді жеке-жеке қарастырамыз:
формуласын қолданып, әрбір қарапайым бөлшектерді жеке-жеке қарастырамыз:
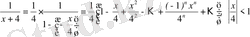 ;
;
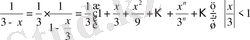 .
.
Табылған жіктеуді (8) -ге қойсақ:
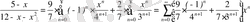 ,
,
және
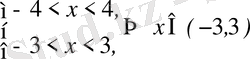 болады.
болады.
Сонымен,
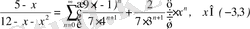 .
.
Мысал 11.
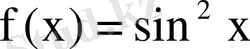 функциясын Тейлор қатарына жікте.
функциясын Тейлор қатарына жікте.
Шешуі.
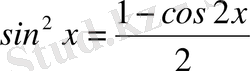 екені бізге мектеп курсынан белгілі. .
екені бізге мектеп курсынан белгілі. .
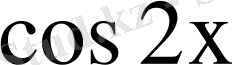 функциясын 3 пункттегі формула бойынша жіктесек (
функциясын 3 пункттегі формула бойынша жіктесек (
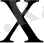 -ті
-ті
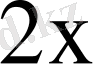 -ке ауыстырсақ), онда:
-ке ауыстырсақ), онда:
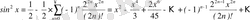 , егер
, егер
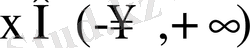 .
.
Мысал 12.
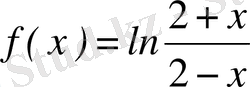 функциясын Тейлор қатарына жікте.
функциясын Тейлор қатарына жікте.
Шешуі.
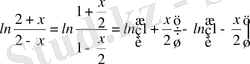 қарастырамыз.
қарастырамыз.
5 пункттегі жіктеуді қолдансақ,
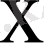 -ті сәйкесінше
-ті сәйкесінше
 және
және
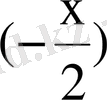 -пен алмастырсақ:
-пен алмастырсақ:

Алынған жіктеу дұрыс болады, егер
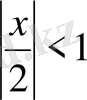 , яғни,
, яғни,
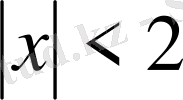 болса.
болса.
Мысал 13.
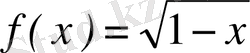 функциясын Тейлор қатарына жікте.
функциясын Тейлор қатарына жікте.
Шешуі.
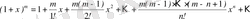 ,
,
мұндағы
 , жіктеуін қолданамыз.
, жіктеуін қолданамыз.
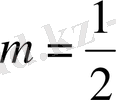 деп алып,
деп алып,
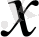 -ті
-ті
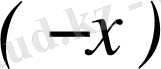 -ке айырбастасақ, онда
-ке айырбастасақ, онда
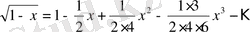 .
.
Жіктеу дұрыс болады, егер
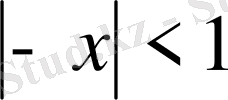 , яғни,
, яғни,
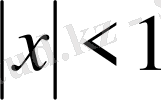 .
.
21. 4 Өз бетімен шығаруға арналған есептер
Келесі есептерді өз беттеріңмен шығарыңдар.
Дәрежелік қатарлардың жинақтылық интервалын тап және интервалдың шектік нүктелерінде жинақтылыққа зертте:
1.
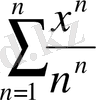 ; 2.
; 2.
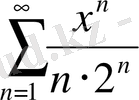 ; 3.
; 3.
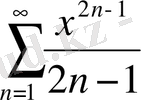 ;
;
4.
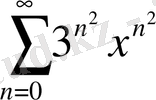 ; 5.
; 5.
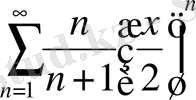 ; 6.
; 6.
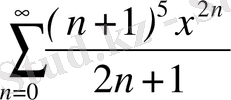 ;
;
7.
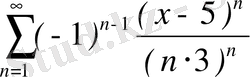 ; 8.
; 8.
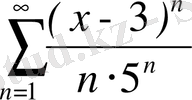 ; 9.
; 9.
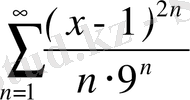 .
.
10. Қатарлардың қосындыларын табыңдар:
а)
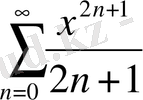 ; б)
; б)
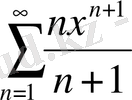 ; в)
; в)
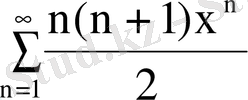 .
.
- 1-5 негізгі жіктеулерін және геометриялық прогрессияны қолданып, келесі функцияларды-тің дәрежелері бойынша жіктеп жаз және жинақтылық интервалын көрсет:
а)
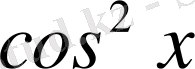 ; б)
; б)
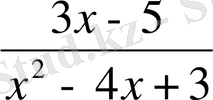 ; в)
; в)
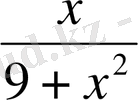 ; г)
; г)
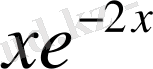 ;
;
д)
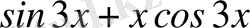 ; е)
; е)
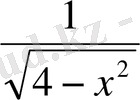 .
.
12.
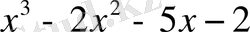 функциясын
функциясын
 -дің дәрежелері бойынша қатарға жікте.
-дің дәрежелері бойынша қатарға жікте.
13.
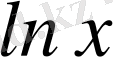 функциясын
функциясын
 -дің дәрежелері бойынша қатарға жікте.
-дің дәрежелері бойынша қатарға жікте.
14.
 функциясын
функциясын
 -дің дәрежелері бойынша қатарға жікте.
-дің дәрежелері бойынша қатарға жікте.
15.
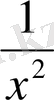 функциясын
функциясын
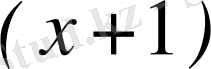 -дің дәрежелері бойынша қатарға жікте.
-дің дәрежелері бойынша қатарға жікте.
21. 5 Сұрақтар
- Функционалдық қатардың анықтамасы.
- Жинақтылық облысы.
- Қатардың бірқалыпты жинақтылығының анықтамасы.
- Мажорланған қатарлар.
- Қатардың қосындысының үзіліссіздігі.
- Қатарды мүшелеп интегралдау.
- Қатарды мүшелеп дифференциалдау.
- Дәрежелік қатарлар. Жинақтылық интервалы.
- Тейлор және Маклорен қатарлары.
- Элементар функцияларды қатарға жіктеу.
1. 1 Екі еселі интегралдың анықтамасы
ХОУ жазықтығында квадратталатын
 тұйық облыста
тұйық облыста
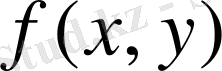 функциясы берілген.
функциясы берілген.
 облысын
облысын
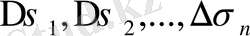 облыстарының ортақ ішкі нүктелері болмайтындай кез келген
облыстарының ортақ ішкі нүктелері болмайтындай кез келген
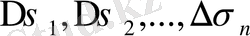 n бөліктерге бөлейік. Әрбір
n бөліктерге бөлейік. Әрбір
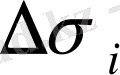 тұйық облысында (ішінде немесе шекарасында) кез келген
тұйық облысында (ішінде немесе шекарасында) кез келген
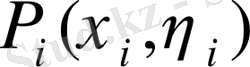 нүктесін таңдаймыз да осы нүктедегі
нүктесін таңдаймыз да осы нүктедегі
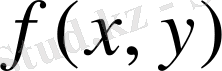 функциясының мәнін
функциясының мәнін
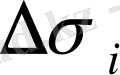 ауданына көбейтеміз. Осындай барлық көбейткіштерді қосып, келесі қосындыны аламыз:
ауданына көбейтеміз. Осындай барлық көбейткіштерді қосып, келесі қосындыны аламыз:
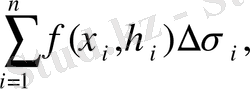 (1)
(1)
бұл
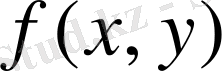 функциясының
функциясының
 облысындағы интегралдық қосындысы деп аталады. Интегралдық қосынды
облысындағы интегралдық қосындысы деп аталады. Интегралдық қосынды
 облысын
облысын
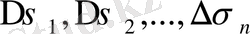 бөліктерге бөлуден және осы бөліктерде
бөліктерге бөлуден және осы бөліктерде
 нүктелерін таңдап алудан тәуелді, яғни
нүктелерін таңдап алудан тәуелді, яғни
 облысындағы
облысындағы
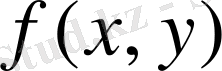 функциясы үшін шексіз көп интегралдық қосындылардың жиынын құруға болады.
функциясы үшін шексіз көп интегралдық қосындылардың жиынын құруға болады.
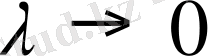
Шектік операцияға көшпес бұрын облыс диаметрі және облысты бөлу қадамы ұғымдарын енгізейік. Тұйық облыстың (екі немесе үш өлшемді кеңістіктегі) диаметрі деп осы облыстың шекарасындағы екі нүктенің ең үлкен арақашықтығын айтамыз. Облысты ақырлы бөліктерге бөлу қадамы деп бөлік облыстардың диаметрлерінің ең үлкенін айтамыз.
 арқылы
арқылы
 облысын
облысын
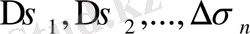 бөліктерге бөлу қадамын белгілейміз. Облысты шексіз ұсақ бөліктерге бөлу және оған сәйкес облысты бөлу п санының шексіз артуынан тұратын процесті «
бөліктерге бөлу қадамын белгілейміз. Облысты шексіз ұсақ бөліктерге бөлу және оған сәйкес облысты бөлу п санының шексіз артуынан тұратын процесті «
 облысын бөлу қадамы нөлге ұмтылады» деп сипаттауға болады.
облысын бөлу қадамы нөлге ұмтылады» деп сипаттауға болады.
Егер
 облысының
облысының
 бөлу қадамы нөлге ұмтылғанда (1) интегралдық қосындының шегі бар болса, онда бұл шекті
бөлу қадамы нөлге ұмтылғанда (1) интегралдық қосындының шегі бар болса, онда бұл шекті
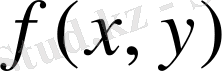 функциясының
функциясының
 облысы бойынша екі еселі интегралы деп атайды және
облысы бойынша екі еселі интегралы деп атайды және
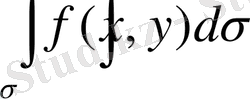 немесе
немесе
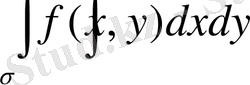 .
.
символдарымен белгілейді. Мұндағы
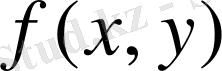 - интеграл астындағы функция,
- интеграл астындағы функция,
 - интегралдау облысы, x және y - интегралдау айнымалылары,
- интегралдау облысы, x және y - интегралдау айнымалылары,
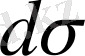 (dxdy) - аудан элементі. Осыдан, анықтама бойынша
(dxdy) - аудан элементі. Осыдан, анықтама бойынша
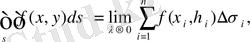
егер бұл шек бар болса.
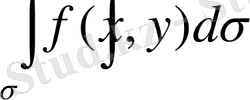 екі еселі интегралы бар
екі еселі интегралы бар
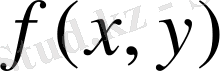 функциясы
функциясы
 облысында интегралданады деп аталады.
облысында интегралданады деп аталады.
1. 2 Екі еселі интегралдың бар болуы және қасиеттері
Шынында да, барлық функциялар үшін
 облысы бойынша екі еселі интеграл табылады ма, егер жоқ болса, қандай функциялар үшін екі еселі интегралдар анықталады деген сұрақ туындайды.
облысы бойынша екі еселі интеграл табылады ма, егер жоқ болса, қандай функциялар үшін екі еселі интегралдар анықталады деген сұрақ туындайды.
 облысында интегралданатын функция
облысында интегралданатын функция
 тұйық облысында шектелген болуы керек, өйткені кері жағдайда
тұйық облысында шектелген болуы керек, өйткені кері жағдайда
 нүктелерін таңдауда интегралдық қосындыны абсолют шамасы бойынша өте үлкен етіп алуға болады, яғни
нүктелерін таңдауда интегралдық қосындыны абсолют шамасы бойынша өте үлкен етіп алуға болады, яғни
 нөлге ұмтылғанда интегралдық қосындының шегі болмас еді.
нөлге ұмтылғанда интегралдық қосындының шегі болмас еді.
Екі еселі интегралдың бар болуының жеткілікті шарттарын қарастырайық.
Теорема 1.
Егер
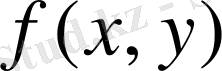 функциясы
функциясы
 тұйық облысында үзіліссіз болса, онда
тұйық облысында үзіліссіз болса, онда
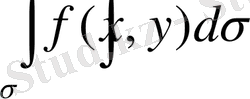 екі еселі интеграл бар болады.
екі еселі интеграл бар болады.
Бұл теореманың дәлелдеуін анықталған интегралдың сәйкес теоремасына сай дәлелдеуге болады.
Теорема 2.
Егер
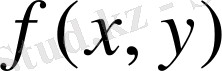 функциясы
функциясы
 тұйық облыста шектелген және үзіліссіз болса, онда
тұйық облыста шектелген және үзіліссіз болса, онда
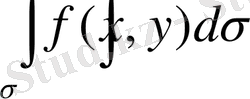 екі
екі
еселі интеграл бар болады. Төмендегі функциялар (1 немесе 2) теореманың шарттарын қанағаттандырады деп ұйғарып, екі еселі интегралдың негізгі қасиеттерін келтірейік. Бұл қасиеттердің дәлелдеуін анықталған интегралдың қасиеттеріне сай дәлелдеуге болады.
1.
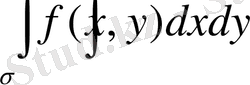 екі еселі интегралы интегралдау айнымалысын белгілеуден тәуелді емес.
екі еселі интегралы интегралдау айнымалысын белгілеуден тәуелді емес.
2. k тұрақты көбейткішті екі еселі интеграл таңбасы алдына шығаруға болады:
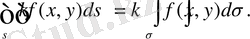
3. Екі функцияның қосындысының екі еселі интегралы осы функциялардың екі еселі интегралдарының қосындысына тең:
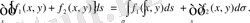
4. Егер
 облысы
облысы
 және
және
 облыстарына бөлінсе, онда
облыстарына бөлінсе, онда
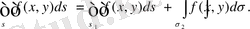
5. Егер барлық
 облысында
облысында
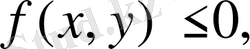
онда
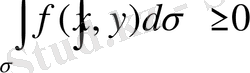
6. Егер барлық
 облысында
облысында
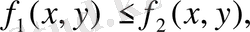
онда
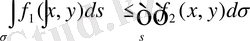
7. Егер
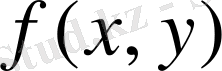 функциясы
функциясы
 облысында берілсе, онда
облысында берілсе, онда
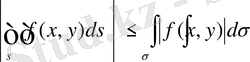
8.
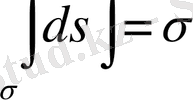
1. 3 Екі еселі интегралдың геометриялық мағынасы
Цилиндрлік дененің көлемін табу есебіне оралайық. Қарастырып отырған
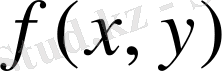 функциясы тұйық
функциясы тұйық
 облысында үзіліссіз болса, онда
облысында үзіліссіз болса, онда
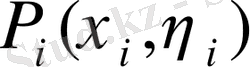 нүктелері
нүктелері
 тұйық облыстарында қандай болса да
тұйық облыстарында қандай болса да
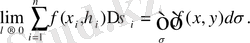
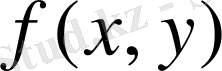 функциясы
функциясы
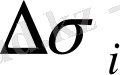 облыстарында (m
i
) ең кіші немесе (M
i
) ең үлкен мәндерін қабылдайтындай етіп,
облыстарында (m
i
) ең кіші немесе (M
i
) ең үлкен мәндерін қабылдайтындай етіп,
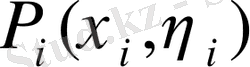 нүктелерін таңдай отырып, келесі теңдікті аламы:
нүктелерін таңдай отырып, келесі теңдікті аламы:
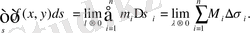
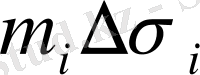 және
және
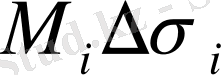 қосылғыштары табаны
қосылғыштары табаны
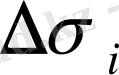 болатын цилцндр көлеміне тең.
болатын цилцндр көлеміне тең.
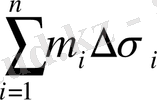 және
және
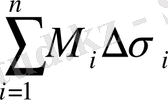 қосындылары сәйкесінше іштей және сырттай сызылған V цилиндрлік денелердің көлемдеріне тең.
қосындылары сәйкесінше іштей және сырттай сызылған V цилиндрлік денелердің көлемдеріне тең.
 бұл көлемдер ортақ шекке ие болады, берілген дене кубталады және оның V көлемі екі еселі интегралға тең:
бұл көлемдер ортақ шекке ие болады, берілген дене кубталады және оның V көлемі екі еселі интегралға тең:
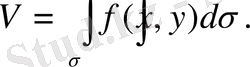
Осыдан екі еселі интегралдың геометриялық мағынасы:
 тұйық облысында теріс емес, үзіліссіз
тұйық облысында теріс емес, үзіліссіз
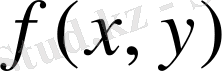 функциясының
функциясының
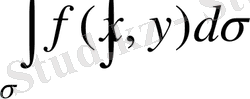 екі еселі интегралы жоғарыдан
екі еселі интегралы жоғарыдан
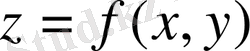 бетпен шектелген, XOY жазықтығындағы табаны
бетпен шектелген, XOY жазықтығындағы табаны
 болатын цилиндрлік дененің көлеміне тең. Егер
болатын цилиндрлік дененің көлеміне тең. Егер
 облысында
облысында
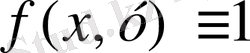 болса, онда цилиндрлік дене табаны
болса, онда цилиндрлік дене табаны
 ал биіктігі
ал биіктігі
 болатын цилиндрді білдіреді. Оның көлемі сан жағынан
болатын цилиндрді білдіреді. Оның көлемі сан жағынан
 табанының ауданына тең. Осылайша, екі еселі интеграл арқылы
табанының ауданына тең. Осылайша, екі еселі интеграл арқылы
 облысының ауданын бұрыннан белгілі формуламен есептейміз
облысының ауданын бұрыннан белгілі формуламен есептейміз
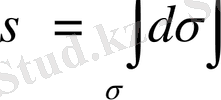 немесе
немесе
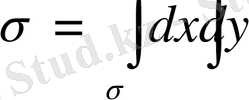 .
.
1. 4 Екі еселі интегралды есептеу жолдары
Екі еселі интегралды есептеу анықталған интегралды есептеуге келтіріледі.
Теорема 1.
Егер
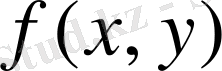 функциясы x=a, y=b (a<b),
функциясы x=a, y=b (a<b),
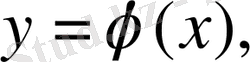
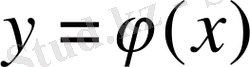
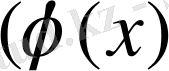 и
и
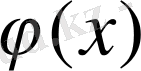 - [a, b] кесіндісінде үзіліссіз функциялар, және осы кесіндіде
- [a, b] кесіндісінде үзіліссіз функциялар, және осы кесіндіде
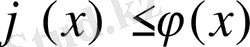 ) сызықтарымен шектелген
) сызықтарымен шектелген
 тұйық облысында үзіліссіз болса, онда
тұйық облысында үзіліссіз болса, онда
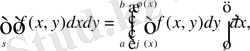 (1)
(1)
екі еселі интегралды есептеуге мүмкіндік беретін теңдік орындалады.
(1) теңдігінің оң жағындағы қайталанбалы интегралы келесі түрде жазылады:
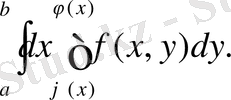
Теорема 2.
Егер
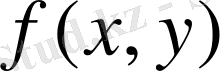 функциясы y=c, y=d (c<d),
функциясы y=c, y=d (c<d),
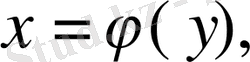 Equation. 3
Equation. 3
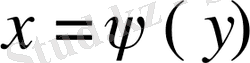 Equation. 3
Equation. 3
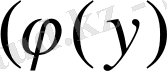 Equation. 3 және
Equation. 3 және
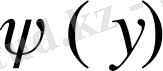 - [c, d] кесіндісінде үзіліссіз және
- [c, d] кесіндісінде үзіліссіз және
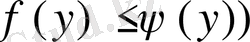 сызықтармен шектелген
сызықтармен шектелген
 тұйық облысында үзіліссіз болса, онда
тұйық облысында үзіліссіз болса, онда
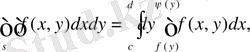 (2)
(2)
екі еселі интегралды есептеуге мүмкіндік беретін теңдік орындалады.
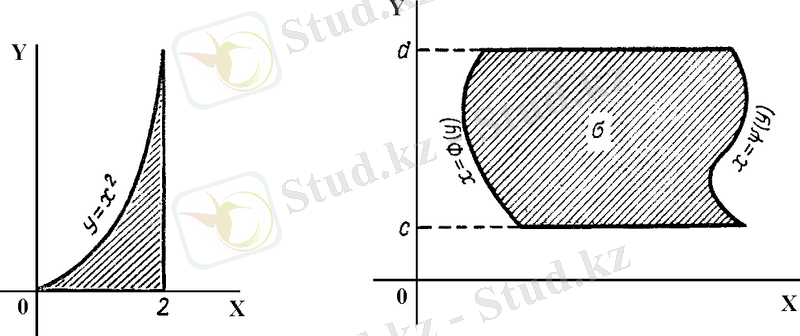
сурет 3. 8. 1
Екі еселі интегралды қайталанбалы интеграл арқылы (2) формуласы бойынша бірінші ішкі интеграл
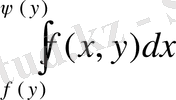 есептеледі, мұнда у тұрақты, өзгеру шектері у-тен тәуелді (
есептеледі, мұнда у тұрақты, өзгеру шектері у-тен тәуелді (
 облысы үшін) . Содан кейін у-тен тәуелді функция
облысы үшін) . Содан кейін у-тен тәуелді функция
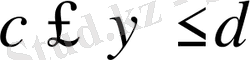 аралығында у бойынша интегралданады.
Мысалы:
аралығында у бойынша интегралданады.
Мысалы:
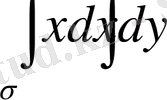 интегралын
интегралын
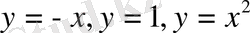 сызықтарымен шектелген
сызықтарымен шектелген
 облысы бойынша есепте.
облысы бойынша есепте.
2 теоремасының шарттары орындалып тұрғандықтан, (2) формуласын қолданамыз:
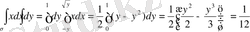 .
.
сурет 3. 8. 2
Егер
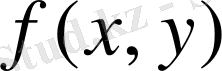 функциясы
функциясы
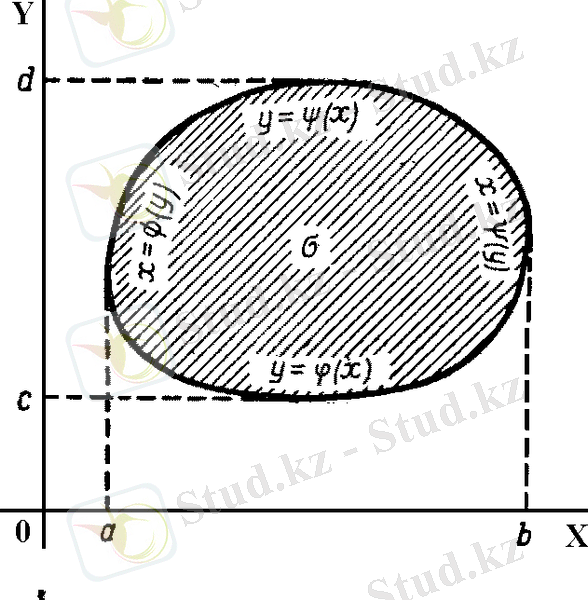
 тұйық облысында үзіліссіз, 1 және 2 теореманың шарттарын бір уақытта қанағаттандырса, онда
тұйық облысында үзіліссіз, 1 және 2 теореманың шарттарын бір уақытта қанағаттандырса, онда
 екі еселі интегралын есептеуде интегралдау ретінің кез келгенін алуға болады (сыртқы интеграл x бойынша, ішкі интеграл y бойынша немесе керісінше) . Мысалы, егер облыс шекарасының ОХ осіне параллель әрбір түзуі және Оу осіне параллель әрбір түзуі тек екі нүктеде қиылысса (3. 8. 2. суреті), онда (1) және (2) формулаларын да қолдануға болады, яғни
екі еселі интегралын есептеуде интегралдау ретінің кез келгенін алуға болады (сыртқы интеграл x бойынша, ішкі интеграл y бойынша немесе керісінше) . Мысалы, егер облыс шекарасының ОХ осіне параллель әрбір түзуі және Оу осіне параллель әрбір түзуі тек екі нүктеде қиылысса (3. 8. 2. суреті), онда (1) және (2) формулаларын да қолдануға болады, яғни
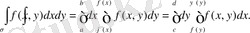
Егер
 облысы - x=a, x=b, y=c және y=d түзулерімен шектелген тік төртбұрыш, ал f(x, y) -
облысы - x=a, x=b, y=c және y=d түзулерімен шектелген тік төртбұрыш, ал f(x, y) -
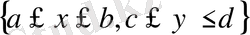 тік төртбұрышында үзіліссіз болса, онда (1) және (2) формулаларын қолданып,
тік төртбұрышында үзіліссіз болса, онда (1) және (2) формулаларын қолданып,
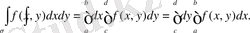
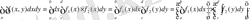
аламыз.
Мысалы, егер
 -
-
 тік төртбұрыш болса, онда
тік төртбұрыш болса, онда
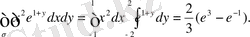
1. 5 Екі еселі интегралдың кейбір геометриялық және механикалық қолданулары
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz