Тармақталған электр тізбектерін талдау: Кирхгоф заңдары, шеңберлік диаграмма және есептеу тәсілдері


КІРІСПЕ
Қазіргі уақытта электр энергиясы барлық өнеркәсіп салаларында транспортта, ауыл шаруашылығында, үй тұрмысында, тағы да басқа халықтың тұрмыс қажетіне пайдаланылады.
Электр техникасы деп электр магниті құбылыстарын практика жүзінде кең салаларда қолданылуын айтамыз. Барлық электр техникасы салалары бір-бірімен байланысты болғандықтан, жоғарғы оқу орындарында Электртізбектерінің теориясы курсын ашуға тура келді. Бұл курс әр түрлі электр техникасы пәндерінің негізі болып саналады.
Осы курстың негізгі бір міндеті, ол құбылыстарды токтар, кернеулер, қуаттар, магнит ағындары т. б. түсініктер арқылы есептеу, зерттеу.
Сондай-ақ тағы бір атқаратын міндеті, ол әр бір құбылыстарды электр кернеулігі, магнит өрісінің индукциясы, қуат ағындары, т. б. түсініктер арқылы есептеу, зерттеу. Осы міндеттердің біріншісі тізбектерді есептеу мен зерттеуге, ал екіншісі электр магниті өрістерін есептеуге, зерттеуге арналған.
Электр техникасының өсіп-дамуы электр магниті құбылыстарын жете зерттеуді, оқып білуді, практика жүзінде пайдалануды қажет етеді. Осы зор еңбекте, ізденуде, көптеген жаңалықтарды ашуда инженерлердің, ғалымдарының қосқан үлесі аз емес. Олар бірлесе отырып электр техникасының маңызды салаларының бастамасына жол ашты. 1845 жылы неміс физигі Г:Кирхгов тармақталған электр тізбектеріне арналған негізгі заңдарын айтты. Сондай-ақ, осы заңдар Кирхгов атымен аталып теориялық және практикалық электр техникасының дамуына зор әсер етті.
Тармақталған Тізбек Үшін Кирхгов Ережелері
Ом заңдары тек қарапайым электр тізбегін есептеу үшін ғана жарамды. Ал күрделі тізбектегі токты аныктау керек болса, онда жалпыланған заңдылықтар болуы қажет. Сондықтан осындай заңдылықтың түріне заряд пен энергияның сақталу заңының салдары ретінде неміс физигі Кирхгов 1824-1887 ашкан заңдар немесе ережелер жатады.
Кирхговтың бірінші ережесі түйіндерге қатысты оған келетін ток пен одан шығатын ток арасындағы байланысты қарастырады. Тармақталған тізбек деп аталатын тізбекте түйіндер үштен кем емес өткізгіштер тоғысатын кез-келген нүктені айтамыз Біз тұрақты токты қарастырғандықтан, түйінге қанша заряд ағып келсе, сонша ағып кетуі керек. Егер түйінге кіретін токтарды оң, ал шығатын токтардытеріс деп есептесек, онда мынадай ережені айтуға болады, түйінде тоғысатын ток күштерінің алгебралық қосындысы нөлге тең. I+I-I=0 Мұны былайша түсінуге болады. Егер түйіндегі токтардың алгебралық қосындысы нөлден өзгеше болса, түйінде зарядтар көбейіп не азайып кетер еді де, бұл өз кезегінде түйіндегі потенциалдың және тізбектен ағатын токтың өзгеруіне әкеп соғар еді. Кирхговтың екінші ережесін жалпы түрде энергияның сақталу заңына сүйеніп, тармақталған тізбек үшін Ом заңын қорытындылау арқылы түсіндіруге болады. Тұйықталған жүйені құрайтын әрбір қосылғыштар энергияларының өзгерістерінің қосындысы нолге тең. Сондықтан тұйық тізбек үшін қатысы орындалады. Бұдан кернеудің түсуі екенін ескерсек, Сонымен Кирхговтың бірінші және екінші ережелеріне сәйкес құрылған тәуелсіз теңдеулердің саны тармақталған тізбектерден өтетін әр түрлі токтардың санына тең болады. Сондықтан электр қозғаушы күші және барлық токты есептеуге болады.
КЕЗ-КЕЛГЕН ТАРМАҚТАЛҒАН ТІЗБЕК ҮШІН ҚҰРЫЛҒАН ШЕҢБЕРЛІК ДИАГРАММАЛАР
- Егер тармақталған тізбектің бір тармағындағы кедергі, мысалы, екінші тармақтағы кедергі өзгеретін болса, ал басқа тармақтардағы кедергі және қоректендіргіштердің Э. Қ. К-і өзгермесе, онда кез-келген тармақтардағы токтар мен кернеулер бір-бірімен түзу сызықты тәуелділікте болады. Бұл тәуелділік тұрақты токқа да және амплитудасы өзгермейтін Э. Қ. К бар синусоидалы токқа да әділетті болады.
- Тізбектің кейбір дербес жағдайда алынған I1бірінші тармақтағы тогы және I2екінші тармақтағы тогы арасындағы байланысты көрсететін формула әділетті I1=A+B+I2мұндағы А және В комплекстік сан. Келесі 1. 1 суретте тармақталған тізбек көрсетілген. Мұнда күрделі схемадан бірінші тармақтағы қоректендіргіштің U1кернеуі және екінші бір тармақтың кедергісі Z2жекеленіп көрсетілген. Тізбектің басқа бөліктері тік төртбұрышты активті элемент ретінде келтірілген, яғни ортасына А әрпі жазылған. Екінші тармақтағы Z2кедергісінің модулі 0+∞ дейін өзгеретін, ал аргументі π өзгермейтін болсын дейік. Сонда барлық тізбекті2кедергісі арқылы қарастырсақ, активті екі ұшты ретінде, онда вектор тогы ұшы I2шеңбер доғасы бойымен жылжиды. Бұл жағдайда да I1ток диаграммасы шеңбер доғасы болатындығын көрсетейік.
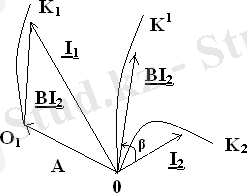
- 1. 2-суретте көрсетілген ОК2доғасы I2тогы шеңберлік диаграммасы болсын дейік. Сонда I2тогын тұрақты коэффициент B=beiβкөбейтсек I векторы ұзындығывесеге ұзарады және β бұрышына бұрылады. Сондықтан В*I2векторының диаграммасы О нүктесі арқылы жүргізілген шеңбердің ОК доғасы болмақ. Негізгі іздестіріп отырған I токтың шеңберлі диаграммасын тұрғызу үшін О нүктесінен а векторын жүргіземіз
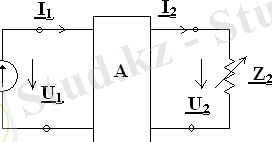
. Тармақталған төртұшты тізбек. 1. 1- сурет
- Шеңберлік диаграмма. 1. 2-сурет
- және оған А векторы ұзындығына тең параллель ОК доғасын көшірсек, ондаО1К1доғасын аламыз. Сонда I1=A+B*I2вектор ұшыО1К1доғасы бойымен жылжитындығын шеңберлі диаграммадан көреміз, яғниО1К1доғасы I тогының шнңберлі диаграммасы болып саналады.
- Қорыта келгенде айтатынымыз, егер кейбір тармақтағы бір кедергісінің модулі ғана өзгерсе және барлық қоректендіргіштердің Э. Қ. К-іөзгермесе, онда кез-келген тармақтағы ток векторы ұшы шнңберлі диаграмманың доғасын сызады. Сонда кез-клген тармақтағы кернеу мен ток арасында түзу сызықты байланыстың бар екендігін білеміз, сондықтан да өзгермелі кернеуге де шеңберлі диаграммасын тұрғызуға болатындығын айту қажет. Енді түзу сызықты тәуелділікті көрсететін формуладағы А және В комплекстік коэффициенттерін қалай табу керектігін келтірейік. Олүшін қандай болса да Z2кедергісінің әр түрлі мәндеріне дәл келетін екі режимдегі I1және I2токтарын білуіміз керек. Мысалы оған, Z2=0 және Z2=∞ режимдері.
- Кедергі Z2=∞ шексіздікке теңелгенде, яғни тізбектегі тармақты ажыратқанда ток I2=0 нөлге тең, бұл бос жүріс режимі деп аталады. I1=Iтең деп алсақ формуладағы байланыстылық I1k=A+Bтең, мұндағы A=I1k, яғни коэффициент А бірінші тармақтағы токқа тең. Енді кедергі Z2=0 нөлге теңелгенде, яғни тізбектегі екінші тармақ қысқа тұйық қосылғанда I2=I2kжәне I1=I1kтең. Осы токтарды формулаға қойсақ I1k=A+B*I2k=I1k+B*I2kмұндағы B=(I1k-I) /I2kсондықтан I1=A+B*I2=I1k+I1k-I1k/I2k*I2Екінші тармақтың ажыратылған кезіндегі сол екінші қысқыштарының арасындағы кернеуді U2kбелгілейік.
- Екінші тармақтағы қысқыштар арқылы қарастырғанда алынған тізбектіегі барлық кедергілердің қосындысын, яғни екінші қысқыштардың кіре берістегі кедергісін Z2kбелгілейік. Сонда активті екіұшты теоремасы бойынша
I 2 =U 2k /Z 2k +Z 2 =U 2k /Z 2k (I+Z 2 /Z 2k ) =I2k/1+Z 2 /Ze ( π-π 2k ) =I 2 /1=Z 2 / Z2kE iΨ
- Екінші қосылғыш түрі формуламен бірдей, демек графикалық түрде I1k-I1kхордасы бар шеңберлі диаграмма ретінде көрсетуге болады. I1тогының шеңберлік диаграммасын құру үшін, алдын ала I1k-I1kжөніне Z2kтабу қажет.
КҮРДЕЛІ ТАРМАҚТАЛҒАН ТІЗБЕКТЕР
Күрделі тармақталған тізбектердің рационалды тәсілін таңдап алу схемалардың ерекшеліктеріне және есептің берілгеніне қарай негізделген.
Тұрақты ток тізбегі үшін есептеу тәсілдерін таңдап алу жайындағы ойлар, синусоидалы ток тізбектері үшін де есептеу тәсілдерін таңдауға қолданылады.
Үшбұрыш болып жалғанған пассив элементтерді, эквивалентті жұлдызша болып жалғанған түрлендіруден кейін немесе керісінше түрленген схеманың комплекстік кедергісі теріс нақты сан бөліктері болуы немесе теріс актив кедергілері болып шығуы мүмкін.
Бұл кедергілер тек таза есептеу мағынасының барлығын ғана көрсетеді.
Мысалы 1. 1 суреттегі тізбекте
Z 1 =Z 2 =(50+j30) Ом ; Z 3 =100 Ом ;
E 1 =100 В ; E 2 = 100e-j30 в барлық токты аныктау керек.
А) контурлы токтар тәсілімен
Б) түйіндік потенциалдар тәсілімен
В) эквивалентті генератордағы кернеу тәсілімен токты анықтауға болады. Ол мысалға Z тармағынан өтетін ток деп қарастыру керек.
Г) қуаттың тепе-теңдігін тексеру керек.
Шешу:а ) контурлы токтардын бағытын қабылдаймыз.
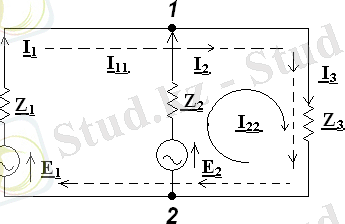
1. 1-сурет. Тармақталған тізбек.
Контурлы токтар тәсілімен схемаға байланысты құрылған теңдеулер жүйесін келтіреміз. I 11 (Z 1 +Z 3 ) + I 22 Z 3 =E 1
I 11 Z 3 +I 22 (Z 2 +Z 3 ) =E 2
Бұл теңдеулерді шеше отырып, мынаны табамыз:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz