Элементар функциялардың анықтамасы мен негізгі қасиеттері: модуль, дәрежелер және логарифмдер, тригонометриялық және кері тригонометриялық функциялар


4. Кейбір элементар функциялардың анықтамасы
және олардың қасиеттері.
4. 1. Нақты санның модулі.
А. 4. 1. 1.
 санның абсолюттік шамасы (немесе модулі) деп, нақты
а
санына айтылады. Егер
а
саны ноль болса, онда ноль, егер
а
саны теріс болса, онда қарама-қарсы
а
санына тең.
санның абсолюттік шамасы (немесе модулі) деп, нақты
а
санына айтылады. Егер
а
саны ноль болса, онда ноль, егер
а
саны теріс болса, онда қарама-қарсы
а
санына тең.
Ф. 4. 1. 1.
Бұл анықтаманы мынадай түрде жазуға болады:
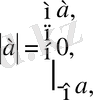
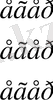
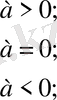
Ф. 4. 1. 2.
Нақты санның модулінің қасиеттері.
1.
2.
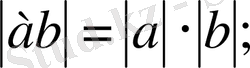
3.
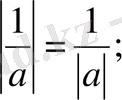 4.
4.
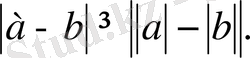
4. 2. Нақты санның дәрежесі және логарифмі.
А. 4. 2. 1.
Егер нақты санның көбейткіші
n
рет алынған болса (
n-
натурал сан,
n>1
) онда ретті дәрежесі деп аталады және
n
көрсеткішті натурал
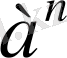 деп көрсетіледі.
деп көрсетіледі.
Анықтама бойынша
 сонымен қатар
сонымен қатар
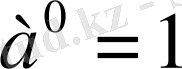 және
және

Ф. 4. 2. 1.
Нақты сандардың натурал дәрежесінің қасиеттері.
1.
 2.
2.
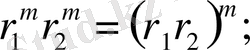
3.
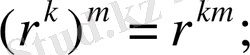 4.
4.
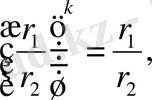 егер
егер
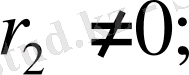
5.
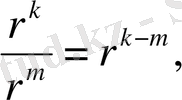 егер
егер
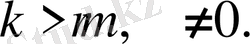
А. 4. 2. 2.
а
-нақты сан,
n-
натурал сан болсын, онда
а
санының дәрежесі теріс емес бүтін көрсеткішті (-
n
) саны айтылады және ол
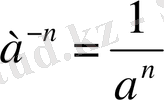 деп белгіленеді.
деп белгіленеді.
А. 4. 2. 3.
Теріс емес
b
саны берілген болсын оның
n
-ші дәрежесі берілген нақты а саны болсын,
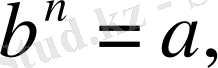 мұның арифметикалық түбірі
а
-ның ішінен алынған
n
және
мұның арифметикалық түбірі
а
-ның ішінен алынған
n
және
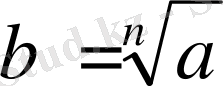 деп аталады.
деп аталады.
Ф. 4. 2. 2.
Анықмама бойынша кез келгеннақты а саны үшін мына теңдік орындалады.
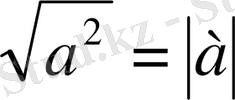
Т. 4. 2. 1.
Кез келген натурал n саны үшін және кез келген теріс емес а сандар үшін, а санының ішінен бірғана n дәрежелі арифметикалық түбір табуға болады.
Ф. 4. 2. 3.
Арифметикалық түбірдің қасиеттері.
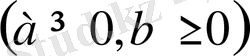
1.
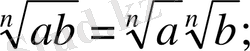 2.
2.
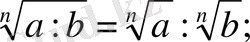
3.
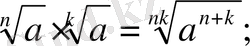 4.
4.
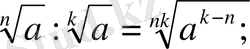
5.
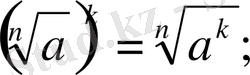 6.
6.
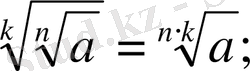
7.
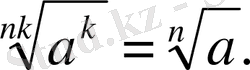
А. 4. 2. 4.
а
нақты, оң сан берілсін және
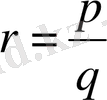 рационал сан жағдй
р
-бүтін сан және
рационал сан жағдй
р
-бүтін сан және
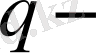 натурал сан
натурал сан
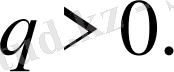
Берілген нақты
b
саны сондай,
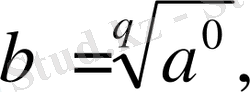 а
- санының рационал дәрежесідеп аталады және
а
- санының рационал дәрежесідеп аталады және
 береді.
береді.
А. 4. 2. 6.
А-теріс, нақты сан берілген болсын,
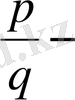 рационал сан, есте ұстайтын жайт
рационал сан, есте ұстайтын жайт
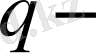 натурал тақ сан,
натурал тақ сан,
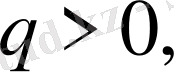 онда
а
-теріс санының рационал дәрежесі деп bсанын айтады, ол
онда
а
-теріс санының рационал дәрежесі деп bсанын айтады, ол
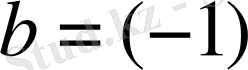
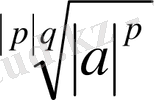 болады.
болады.
А. 4. 2. 6.
Нақты санның нақты дәрежесі. Бізге нақты
а
саны және (рационал немесе иррационал) нақты
х
саны берілген болсын. А- санының нақты дәрежесі деп
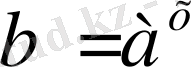 санына айтылады, ол келесі түрмен анықталады.
санына айтылады, ол келесі түрмен анықталады.
А. 2. 7.
Анықтама бойынша
х
санының ең жақын мәні артығымен және кемшілігін
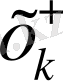 және
және
 деп сәйкесінше белгілейміз. Бұл жағдайда
b
сондай сан, ол барлық
деп сәйкесінше белгілейміз. Бұл жағдайда
b
сондай сан, ол барлық
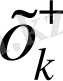
 жақын мәндерінде мына теңсіздіктер орындалады:
жақын мәндерінде мына теңсіздіктер орындалады:
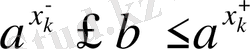 .
.
Егер
0<a<1
және
х>0
, онда
b
-сондай сан,
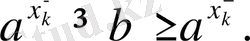
Егер
х>0
болса онда
b
мына теңсіздікпен анықталады.
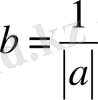
Егер
а=1
болса, онда кез келген
х
үшін мынау анықталады

Теріс санның нақты дәрежесі және ноль анықталмаған.
Ф. 4. 2. 4.
Нақты дәрежелі оң санның қасиеттері
1.
2.
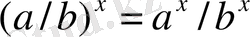
3.
4.
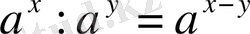
5.
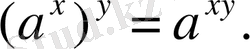
Нақты
а
және
b
оң сандары берілсін. Сондай
х
нақты санын табуды қажет етеді, ол


Т. 4. 2. 2.
Кез келген
а
және
b
нақты сандар жұбы үшін, сондай
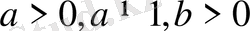 болғанда
х
деген бірғана сан табылады, ол
болғанда
х
деген бірғана сан табылады, ол
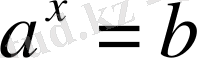 .
.
А. 4. 2. 7.
Егер
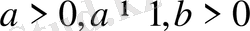 сондаяқ
сондаяқ
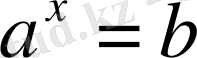 болса
х
нақты саны
b
санының
а
негіздегі логарифмі деп аталып былай жазылады.
болса
х
нақты саны
b
санының
а
негіздегі логарифмі деп аталып былай жазылады.
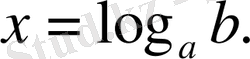
Ф. 4. 2. 5.
Логарифмнің анықтамасы бойынша мыналар орындалады.
1.
2.
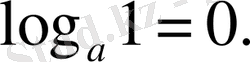
Ф. 4. 2. 6.
Логарифмнің негізгі тепе-теңдігі
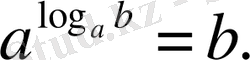
Ф. 4. 2. 7.
Логарифмнің негізгі қасиеттері. x, y, a, b оң ссандары берілген болсыр,
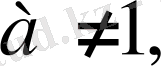
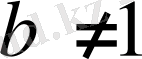 екенінеске сала кетейік және шығарылған нақты
екенінеске сала кетейік және шығарылған нақты
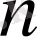 және
және
 сандары. Онда келесі қасиеттер орындалады.
сандары. Онда келесі қасиеттер орындалады.
1.
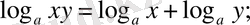 2.
2.
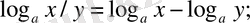 3.
3.
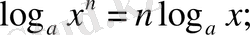
4.
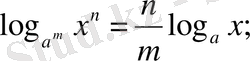 5.
5.
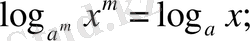 6.
6.
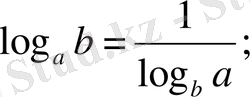
7.
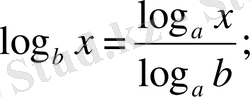 8. егер
8. егер
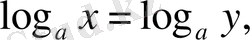 онда
онда
 керісінше;
керісінше;
9. егер
 онда
онда
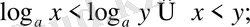
10. егер
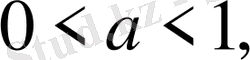 онда
онда
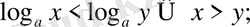
4. 3. тригонометриялық функция .
Тригонометриялық функция ұғымын анықтау үшін, центрі координата басында орналасқан бірлік шеңбер қарастырылады. Кез келген нақты
а
саны үшін осы шеңберден радиус өткізуге болады, және
Ох
осімен құрылған
 бұрышы берілген. (сағат стрелкасына қарсы бағыт оң деп есептелінеді) .
бұрышы берілген. (сағат стрелкасына қарсы бағыт оң деп есептелінеді) .
 бұрышын жасайтын
ON
бірлік радиусының соңы
Q(a, b)
нүктесімен сәйкес келсін, онда
бұрышын жасайтын
ON
бірлік радиусының соңы
Q(a, b)
нүктесімен сәйкес келсін, онда
 бұрыш жасайтын
Q
нүктенің координаттарын радиустың соңы депатап былай жазамыз.
N(a, b) .
бұрыш жасайтын
Q
нүктенің координаттарын радиустың соңы депатап былай жазамыз.
N(a, b) .
А. 4. 3. 1.
 бұрыш жасайтын, соңы бірлік радиутың ординатасына тең санды
бұрыш жасайтын, соңы бірлік радиутың ординатасына тең санды
 бұрыштың синусы деп аталады және
sin
бұрыштың синусы деп аталады және
sin
 деп белгіленеді.
деп белгіленеді.
А. 4. 3. 2.
 бұрыш жасайтын, соңы бірлік радиустың абсциссасына тең санды
бұрыш жасайтын, соңы бірлік радиустың абсциссасына тең санды
 бұрышының косинусы деп аталады және
cos
бұрышының косинусы деп аталады және
cos
 деп белгіленеді.
деп белгіленеді.
А. 4. 3. 3.
 бұрышының синусына байланысты,
бұрышының синусына байланысты,
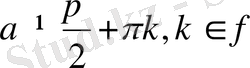 сол бұрышының косинусына қатынасы
сол бұрышының косинусына қатынасы
 бұрыштың тангенсі деп аталады және
tg
бұрыштың тангенсі деп аталады және
tg
 деп белгіленеді.
деп белгіленеді.
А. 4. 3. 4.
 бұрышының косинусына байланысты
бұрышының косинусына байланысты
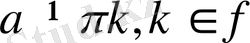 , сол бұрыштың синусына қатынасы
, сол бұрыштың синусына қатынасы
 бұрыштың котангесі деп аталады және
ctg
бұрыштың котангесі деп аталады және
ctg
 деп белгіленеді.
деп белгіленеді.
Ф. 4. 3. 1.
Негізігі тригонометриялық тепе-теңдік. Кең келген бұрышынына мына теңдік орындалады.

Ф. 4. 3. 2.
Бір бұрышты функциялар арасындағы байланыс.
1.
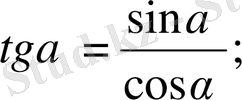 2.
2.
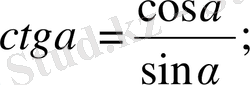 3.
3.
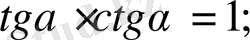
4.
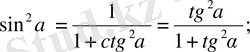 5.
5.
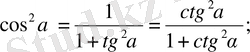
Ф. 4. 3. 3.
Қосу және азайту формулалары.
1.
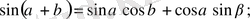 2.
2.
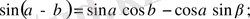
3.
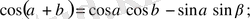 4.
4.
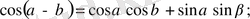
5.
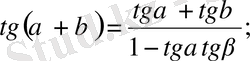 6.
6.
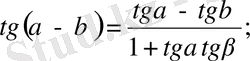
Ф. 4. 3. 4.
Екіленген, үштенген және жартылай бұрыштардың формулалары.
1.
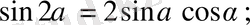 2.
2.
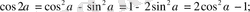
3.
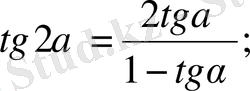 4.
4.
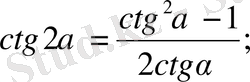
5.
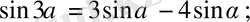 6.
6.
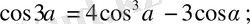
7.
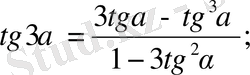 8.
8.
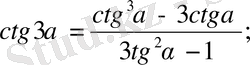
9.
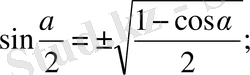 10.
10.
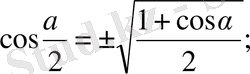
11.
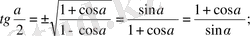
12.
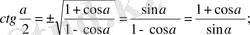
9-12 формулалардың салдары дәрежені төмендету формуласы
9.
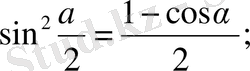 10.
10.
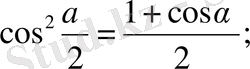
11.
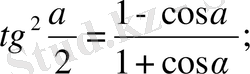 12.
12.
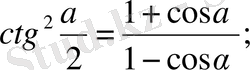
Ф. 4. 3. 5
Тригонометриялық функцияның қосындыларына өзгеріс енгіземіз
1.
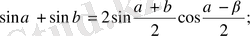 2.
2.
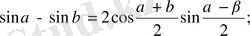
3.
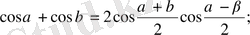 4.
4.
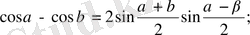
5.
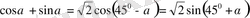
6.
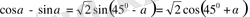
7.
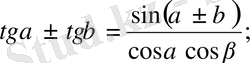 8.
8.
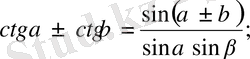
9.
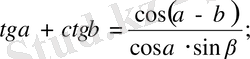 10.
10.
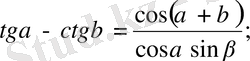
11.
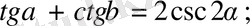 12.
12.
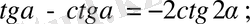
13.
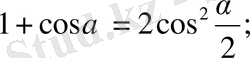 14.
14.
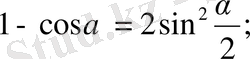
15.
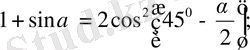 16.
16.
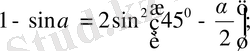
17.
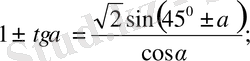 18.
18.
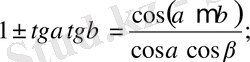
19.
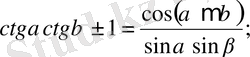 20.
20.
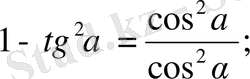
21.
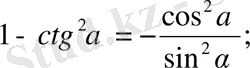 22.
22.
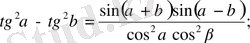
23.
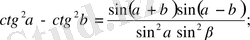
24.
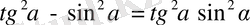 25.
25.
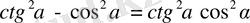
Ф. 4. 3. 6.
Қосындының туындысына өзгеріс енгізу
1.
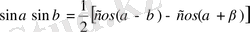 2.
2.
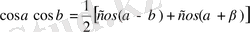
3.
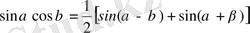
Ф. 4. 3. 7.
Әмбебап (қолайлы) тригонометриялық орналастыру
1.
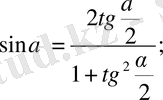 2.
2.
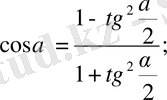 3.
3.
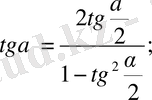
Ф. 4. 3. 8.
Кейбір маңызды ара қатынас.
1.
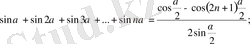
2.
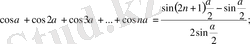
3.
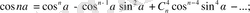
4.
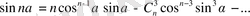
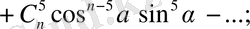
Ф. 4. 3. 9.
Келтірілген формулалар
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz