Жазықтықтың теңдеулері

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Жазықтықтың теңдеулері

1) Берілген М ₀ (x ₀ ; y ₀ ; z ₀ ) нүктесі арқылы өтетін және нольдік емес нормаль 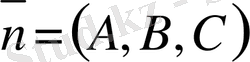векторына перпендикуляр болатын жазықтықтың теңдеуі

A(x - x ₀ ) + B(y - y ₀ ) + C(z - z ₀ ) = 0 (1)

2) Жазықтықтың жалпы теңдеуі

Ax + By + Cz + D = 0, (2)

мұнда А2 + В ² + С ² ≠ 0.

Жалпы теңдеумен анықталған жазықтықтың орналасуы:

а) D = 0 , сонда Ау + Сz = 0 жазықтығы бас нүктеден өтеді. Керісінше тұжырым да дұрыс.

б) А = 0 , сонда Ву + Сz + D = 0 жазықтығы абсциссалар (Ох) осіне параллель болады. осы сияқты, В = 0 болғанда (2) теңдеу Оу осіне, ал С = 0 болғанда, Оz осіне параллель жазықтықты анықтайды.

в) А = 0 , В = 0 , сонда Сz + D = 0 - апликаталар (Оz) осіне перпендикуляр (Оху) жазықтығына параллель болатын жазықтықтың теңдеуі.

А = 0 , В = 0 , сонда Сz + D = 0 жазықтығы Оу осіне перпендикуляр ( Оху жазықтығына параллель) ;

В = 0 , С = 0 , сонда Ах + D = 0 жазықтығы Ох осіне перпендикуляр ( Оху жазықтығына параллель) болатын жазықтықты анықтайды.

г) А = 0 , С = 0 , сонда (2) теңдеу Ох осі арқылы;

В = 0 , D = 0 , сонда (2) теңдеу Оу арқылы;

С = 0 , D = 0 , сонда (2) теңдеу Оz осі арқылы өтеді.

д) А = 0 , В = 0 , D = 0 , сонда (2) теңдеу Оху жазықтығымен беттеседі

(z = 0) ;

А = 0 , С = 0 , D = 0 , сонда (2) теңдеу Охz жазықтығымен беттеседі

(у = 0) ;

В = 0 , С = 0 , D = 0 , сонда (2) теңдеу Оуz жазықтығымен беттеседі

(х = 0) .

3) A ₁ x + B ₁ y + C ₁ z + D ₁ = 0 және A ₂ x + B ₂ y + C ₂ z + D ₂ = 0 теңдеулерімен анықталынған екі жазықтық арасындағы бұрышты анықтайтын формула

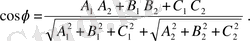(3)

Екі жазықтықтың параллель болу белгісі

;

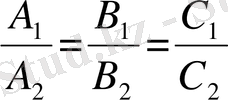Екі жазықтықтың перпендикуляр болу белгісі

A ₁ A ₂ + B ₁ B ₂ + C ₁ C ₂ = 0

4) М ₀ (x ₀ ; y ₀ ; z ₀ ) нүктесінен Ax + By + Cz + D = 0 теңдеуімен анықталатын жазықтыққа дейінгі қашықтықты есептейтін формула

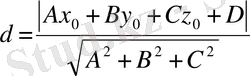. (4)

5) Берілген А ₀ (x ₁ ; y ₁ ; z ₁ ), В(x ₂ ; y ₂ ; z ₂ ) және С(x ₃ ; y ₃ ; z ₃ ) нүктелері арқылы өтетін жазықтықты анықтайтын формула

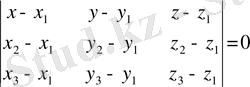. (5)

6) Жазықтықтың «кесінділерде» берілген теңдеуі

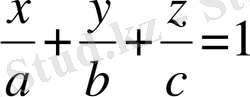. (6)

мұнда .

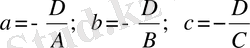7) Жазықтықтың нормаль түрдегі теңдеуі

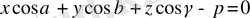. (7)

Мұнда, cosα, cosβ, cosγ - координаттар бас нүктесінен жазықтыққа бағытталған нормаль вектордың бағыттаушы косинустары; р > 0 - О(0; 0; 0) нүктесінен жазықтыққа дейінгі ара қашықтық.

Ax + By + Cz + D = 0 теңдеуін 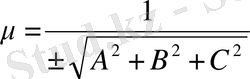нормальдаушы көбейткішке көбейтіп, жазықтықтың нормаль түрдегі теңдеуін аламыз ( μ - дың таңбасы D - нің таңбасына қарама-қарсы етіп таңдап алынады ) .

3 - мысал . М (2; -1; 4) нүктесінен өтетін және 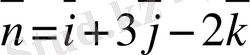векторына перпендикуляр болатын жазықтықтың теңдеуін жазу керек.

Шешуі: (1) формуланы пайдаланамыз: А = 1, В = 3, С = -2.

1· (х - 2) + 3 · (у + 1) - 2· (z - 4) = 0 → х - 2 + 3у + 3 - 2z + 8 = 0 →

→ х + 3у - 2z + 9 = 0.

4 - мысал . 2х - 3у + z + 1 = 0 және 3х + у - 2z + 7 = 0 жазықтарының арасындағы бұрышты анықтау керек.

Шешуі: (3) формуланы пайдаланамыз: А ₁ = 2, В ₁ = -3, С ₁ = 1 және

А ₂ = 3, В ₂ = 1, С ₂ = -2 . Сонда

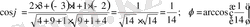5 - мысал . М ₀ (1; -5; 6) нүктеден 6х - 3у + 2z - 38 = 0 жазықтыққа дейінгі ара қашықтықты табу керек.

Шешуі: (4) формуланы пайдаланамыз: А = 6, В = -3, С = 2.

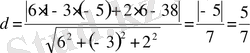6 - мысал . М(1; -2; 3) нүктесі арқылы өтетін 5х - 3у + 2z - 10 = 0 жазықтығына параллель болатын жазықтықтың теңдеуін жазу керек.

Шешуі: (1) формула бойынша

A(x - 1) + B(y + 2) + C(z - 3) = 0.

Ізделінді жазықтықтың нормаль векторы берілген жазықтықтың нормаль векторымен сәйкес келеді (екі параллель болу белгісі) : А = 5, В = -3, С = 2. Сонда

5(x - 1) - 3(у + 2) + 2(z - 3) = 0 → 5х - 3у + 2z - 17 = 0.

7 - мысал . М ₁ (2; 3; 3), М ₁ (2; 0; -5), М ₁ (0; 3; -5) нүктелері арқылы өтетін жазықтықтың теңдеуін жазу керек.

Шешуі: (5) формуланы пайдаланамыз:

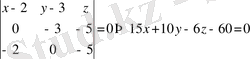8 - мысал . М(3; -1; -5) нүктесінен өтіп 3х - у + z + 5 = 0 және

х - 4у + 3z + 2 = 0 жазықтықтарына перпендикуляр болатын жазықтықтың теңдеуін жазу керек.

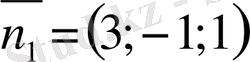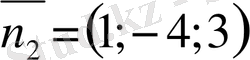Шешуі: Берілген жазықтықтардың нормаль векторларының және векторлық көбейтіндісі ізделінді жазықтықтың нормаль векторы болатындығына көз жеткізу қиын емес